математика

Поделиться статьей в социальных сетях:

в избранное

Дилемма заключенного

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 4 сентября 1997 года; содержательно переработано 29 августа 2014 года.

Два злоумышленника были задержаны за ограбление Сберегательного банка Гиберния и отправлены в разные одиночные камеры. Каждый из них куда больше заботился о своей личной свободе, чем о благополучии сообщника. Опытный прокурор сделал каждому следующее предложение: «Вы можете признаться или промолчать. Если вы признаетесь, а ваш сообщник сохранит молчание, я сниму все обвинения против вас и использую ваши показания с тем, чтобы ваш сообщник получил серьезный срок. Аналогичным образом, если ваш сообщник признается, в то время как вы будете молчать, то он выйдет на свободу, а вы будете отбывать срок. Если вы оба согласитесь и я получу два признания виновности, то я прослежу, чтобы вы оба получили раннее условно-досрочное освобождение. Если вы оба будете молчать, я буду вынужден обвинить вас как минимум в незаконном владении огнестрельным оружием. Если вы пожелаете дать показания, вы должны передать записку тюремщику перед моим возвращением завтра утром».

Дилемма, с которой столкнулись заключенные, состоит в том, что безотносительно от индивидуального выбора соучастника каждому из них лучше дать показания, нежели промолчать. Но полученный при обоюдном признании результат будет хуже для каждого из них, чем результат, которого они бы достигли, если бы оба сохранили молчание. Принято считать, что данная головоломка служит примером конфликта между индивидуальной и групповой рациональностью. Группа, участники которой преследуют рациональный личный интерес, может оказаться в худшей ситуации, нежели группа, участники которой поступают вопреки такому интересу. Если брать шире, если платежи (выигрыши) не представляют личной выгоды, то группа, участники которой рационально преследуют любые цели, может в целом достигнуть меньшего успеха, чем если бы они не преследовали цели в индивидуальном порядке. В связи с этим исследователи также полагают, что игра «дилемма заключенного» и ее обобщения со многими игроками моделируют знакомые ситуации, в которых трудно заставить рациональных эгоистичных агентов сотрудничать ради общего блага. Большая часть новейших комментариев сосредоточена на установлении условий, при которых игроки сделают или должны совершить «кооперативный» ход, заключающийся в сохранении молчания.

Несколько отличная трактовка представляет игру в качестве ситуации выбора между эгоистичным поведением и желательным с точки зрения общества альтруизмом. Ход, которому соответствует признание, приносит действующему лицу пользу независимо от поступков другого игрока, в то время как ход, которому соответствует молчание, приносит пользу другому игроку независимо от того, что тот делает. Конечно, принесение блага в первую очередь себе не во всех случаях несправедливо, а принесение пользы другим в ущерб самому себе не всегда обязательно с точки зрения морали, однако в дилемме заключенного оба игрока предпочли бы результат, достигаемый альтруистическими ходами, результату с эгоистичными ходами. В связи с этим Дэвид Готье и другие исследователи утверждают, что дилемма заключенного говорит нам нечто важное о природе нравственности. 

Вот другая история. У Билла есть синяя кепка, но он предпочел бы красную, в то время как у Роуз есть красная кепка, а она предпочла бы синюю. Оба предпочли бы иметь две кепки или хотя бы одну, чем не иметь кепки вообще. Каждому предоставлен выбор между сохранением кепки, которую они имеют, и передачей ее другому. Эта «игра в обмен» имеет ту же самую структуру, что и история о заключенных. Сохраняет ли Роуз свою кепку или отдает ее Биллу, Биллу более выгодно сохранение кепки, а Роуз более выгодно, если он отдаст свою кепку ей. Сохраняет ли Билл свою кепку или отдает ее Роуз, для Роуз более выгодно сохранение кепки, а Биллу более выгодно, если он отдаст свою кепку ей. Однако обоим выгоднее, если они обменяются кепками, чем если бы оба сохранили то, что имеют. Новая история предполагает, что дилемма заключенного лежит также в основе нашей экономической системы. Представляется, что любой рынок, созданный для облегчения взаимовыгодных обменов, должен будет преодолеть дилемму или избежать ее.

Головоломки, устроенные наподобие дилеммы заключенного, были разработаны и прокомментированы Меррилом Флудом и Мелвином Дрешером в 1950 году в рамках исследований корпорации RAND в области теории игр (которые корпорация проводила из-за их возможных применений в глобальной ядерной стратегии). Название «дилемма заключенного» и версия с приговорами как платежами была предложена Альбертом Такером, который хотел сделать идеи Флуда и Дрешера более доступными для аудитории стэнфордских психологов. Хотя сами Флуд и Дрешер не стремились обнародовать свои идеи в открытых журнальных статьях, головоломка с тех пор стала привлекать все более широкое внимание в разнообразных областях. Доннинджер сообщает, что в шестидесятых и семидесятых по этому вопросу было издано «свыше тысячи статей». Библиография (Axelrod и D’Ambrosio 1996) публикаций в период между 1988 и 1994 годами, связанных с исследованием Роберта Аксельрода на данную тему, содержит 209 источников. Поиск словосочетания «дилемма заключенного» в Google Scholar на 2014 год выдает 106 000 ссылок.

Ниже рассматривается разнообразие более точных определений дилеммы заключенного начиная с самого узкого, а также некоторые связи ее со схожими играми и некоторыми применениями в философии и в других дисциплинах. Особое внимание уделяется «эволюционным» версиям игры, в которых члены популяции играют друг с другом неоднократно и те, кто добивается более высоких платежей, «воспроизводятся» быстрее, чем те, кто получает более низкие платежи. Дилемма заключенного далее будет обозначаться аббревиатурой «ДЗ» (в случае ссылок на перечни формальных условий игры используется сокращение PD ).

Симметричная ДЗ 2×2 с ординальными платежами

В самой простой форме ДЗ — игра, описанная платежной матрицей следующего вида:

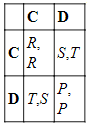
Она удовлетворяет следующей цепи неравенств:

(PD1)         T>R>P>S

Имеются два игрока, Ряд и Колонка. Каждый имеет два возможных хода, «сотрудничать» (cooperate, C) и «предать», или «отказаться от сотрудничества» (defect, D), которые означают соответственно варианты сохранения молчания и признания в указанном хрестоматийном примере. Для каждой возможной пары ходов платежи Ряда и Колонки (именно в таком порядке) указаны в соответствующей ячейке. R является платежом по типу «награды» (reward), который получает каждый игрок, если оба сотрудничают. P является «наказанием» (punishment), которое каждый получает, если оба предают. T является «искушением» (temptation), получаемым единственным предателем, а S является платежом по типу «простак» (sucker), получаемым единственным сотрудничающим. Мы предполагаем здесь, что игра симметрична, т.е. платежи по типам награда, наказание, искушение или простак являются одинаковыми для каждого игрока и имеют только порядковое (ординальное) значение, т.е. указывают, лучше ли один платеж другого, но не говорят о том, в какой мере лучше. Теперь легко увидеть, что перед нами структура дилеммы, схожая с изложенной выше историей. Предположим, что Колонка сотрудничает. Тогда Ряд получает R за сотрудничество и T за предательство, и поэтому предательство становится более выгодным. Предположим, Колонка предает. Тогда Ряд получает S за сотрудничество и P за предательство, и поэтому последнее вновь становится более выгодным. В таком случае говорится, что ход D Ряда строго доминирует ход C: независимо от того, что делает Колонка, Ряду лучше избрать D, нежели C. У Колонки в силу симметрии D также строго доминирует C. Таким образом, два «рациональных» игрока будут предавать и получать платеж P, в то время как «иррациональные» игроки могут сотрудничать и получать больший платеж R. В стандартных подходах теория игр предполагает рациональность и общее знание. Каждый игрок рационален, знает, что другой также рационален, знает, что другому известно, что он рационален, и т.д. Каждый игрок также знает, как другой оценивает результаты. Однако поскольку D строго доминирует C для обоих игроков, аргументация в пользу дилеммы здесь требует только того, чтобы каждый игрок знал о своих собственных платежах. (Довод остается справедливым, разумеется, лишь при наиболее строгих стандартных допущениях.)

Также стоит отметить, что исход (D,D), при котором оба игрока предают, — уникальное сильное равновесие Нэша игры, т.е. это единственный результат, при котором каждый игрок мог лишь ухудшить ситуацию, в одностороннем порядке изменив свой ход. Интерес Флуда и Дрешера к их дилемме был обусловлен тем, что, по их мнению, она опровергала утверждение, согласно которому равновесие Нэша игры определяет ее естественные «решения».

Если в ранжированиях платежей могут быть «связи», условие PD1 можно ослабить, не разрушая при этом суть дилеммы. Предположим, что верно одно из следующих условий:

(PD2)    T>R>P≥S или

             T≥R>P>S

Тогда для каждого игрока, хотя D строго не доминирует C, D все же слабо доминирует в том смысле, что успех каждого игрока всегда по меньшей мере такой же, а иногда более крупный, при выборе D. При этих условиях по-прежнему представляется рациональным избирать D, что вновь приводит к платежу, который не является предпочтительным для обоих игроков. Назовем игру, которая отвечает PD2, слабой ДЗ. Отметим, что в слабой ДЗ, которая не отвечает взаимному предательству PD1, больше не имеется равновесия Нэша в строгом смысле, определенном выше. Однако в ней все еще остается равновесие Нэша в более слабом смысле, так как ни один из игроков не может улучшить свое положение, изменив свой ход в одностороннем порядке. Опять же можно предположить, что если есть уникальное равновесие Нэша такой более слабой разновидности, рациональные корыстные игроки достигли бы его.

Асимметрия

Если предположить, что ситуация не симметрична, ДЗ может быть представлена посредством подстрочных индексов r и c для платежей Ряда и Колонки. 

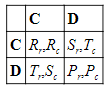
Если мы допускаем, что платежи для каждого игрока располагаются в прежнем порядке, т.е. Ti>Ri>Pi>Si, когда i=r,c, то D, как и прежде, является строго доминирующим ходом для обоих игроков, однако результат (D,D) для обоих игроков, совершающих этот ход, хуже, чем (C,C). Мощь дилеммы ощущается теперь и при более слабых условиях. Рассмотрим следующие три пары неравенств:

(PD3)

a. Tr>Rr и Pr>Sr

b. Tc>Rc и Pc>Sc

c. Rr>Pr и Rc>Pc

При выполнении всех этих условий аргументация в пользу дилеммы выстраивается прежним образом. Предательство строго доминирует сотрудничество для каждого игрока, и (C,C) строго предпочитается каждым по сравнению с (D,D). При замене одного из двух знаков «>» в каждом из условий «а – c» на знак нестрогого неравенства «≥» мы получаем слабую ДЗ. D слабо доминирует C для каждого игрока (т.е. D является столь же хорошим, как C, во всех случаях и лучше в некоторых), и (C,C) в слабом смысле лучше, чем (D,D) (т.е. как минимум столь же хорош для обоих игроков и лучше для одного). Так как ни один из пунктов не требует сравнений платежей с индексами r и c, нам необязательно допускать, что «>» имеет какую бы то ни было «межличностную» значимость.

Теперь предположим, что мы отбрасываем первое неравенство в отношении a или b (но не обоих). Игру, которая отвечает таким условиям, можно было бы назвать ДЗ с общим знанием. Пока каждый игрок знает, что другой рационален, и каждый из них также знает распределение платежей другого, мы все еще ощущаем мощь дилеммы. Предположим, что выполняется неравенство а. Тогда D является доминирующим ходом для Ряда. Колонка, которой известно, что Ряд поступает рационально, знает, что Ряд предаст, и поэтому при сохранении неравенства в b также предаст. Точно так же, если выполняется b, Колонка откажется от сотрудничества, а Ряд, понимая это, решит предать сам. В соответствии с неравенством c, результирующее (D,D) для обоих вновь окажется хуже, нежели (C,C).

Множество ходов и опциональная ДЗ

В общем и целом можно сказать, что ДЗ представляет собой игру, в которой «кооперативный исход» (достигаемый лишь в том случае, если каждый игрок поступается рациональной корыстью) однозначно предпочитается «эгоистичному» исходу, когда каждый игрок придерживается рационального личного интереса. Мы можем охарактеризовать эгоистичный исход либо как следствие того, что каждый из игроков преследует свою доминирующую (или строго доминирующую) стратегию, либо как уникальное слабое (или строгое) равновесие Нэша. В двухходовой игре оба описания относятся к одному и тому же явлению — пара доминирующих ходов является уникальным равновесием, а уникальное равновесие является парой доминирующих ходов. Тем не менее, как показывает матрица ниже, приведенные определения не совпадают в игре с бо́льшим количеством ходов.

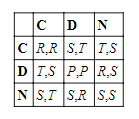
Здесь каждый игрок может выбрать «сотрудничество» (C), «предательство» (D) или «иное» (N). Платежи распределяются в прежнем порядке. Предательство более не является доминирующей стратегией, поскольку для каждого из игроков будет лучше выбрать C, а не D, когда его соперник выбирает N. Однако (D,D) все еще служит уникальным равновесием. Обозначим игру, в которой эгоистичный исход выступает уникальным равновесием, как равновесную ДЗ, а игру, в которой эгоистичный исход является парой доминирующих ходов, как доминирующую ДЗ. Как будет показано ниже, попытки «решить» ДЗ допуском условных стратегий могут создать многоходовые игры, которые сами по себе окажутся равновесными ДЗ.

Трехходовые игры, устроенные немного по-другому, также привлекли к себе внимание. Они были названы «опциональной ДЗ». (См., напр., Kitcher 2011, 1993; Batali and Kitcher 1995; Szabу and Hauert 2002; Orbell and Dawes 1993, а также 1991.) Согласно первым трем источникам, опциональные игры также позволяют игрокам оповещать о своей готовности участвовать во взаимодействии (т.е. выбрать C или D) с конкретными противниками. Простые трехходовые игры без оповещения, разобранные в данном разделе, называются «полуопциональными» (Batali and Kitcher 1995). Платежи S,R,P и T распределяются в прежнем порядке, но платежная матрица теперь содержит дополнительное значение «выхода из игры» (уклонения), O, которое располагается между P и R.

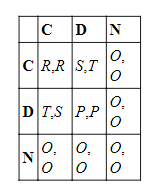
В этой версии игры предательство более не является доминирующим ходом, а взаимное предательство — равновесным исходом. Если Колонка сотрудничает, Ряд преуспевает, предавая; если Колонка предает, Ряд преуспевает, играя N; и если Колонка играет N, тогда Ряд, играя любой ход, преуспевает равным образом. Из исхода взаимных D любой игрок может извлечь выгоду, переключаясь в одностороннем порядке на N. Однако из результата взаимных N никакая сторона не может извлечь выгоду, изменяя ходы в одностороннем порядке. Таким образом, опциональная ДЗ является слабой равновесной ДЗ с N в роли предательства. Орбелл и Доуз добавляют еще одно условие: платеж выхода из игры O равен нулю (Orbell and Dawes 1991, 1993). В опциональной ДЗ рациональный игрок будет участвовать (т.е. будет играть C или D), если и только если он ожидает, что его противник решит сотрудничать. Ведь если ее противник решит сотрудничать, то ей будут гарантированы как минимум R при участии и точно O при неучастии, тогда как в противном случае ей будут гарантированы самое большее P при участии и точно O при неучастии. Это ярче всего проявляется, когда O имеет нулевое значение, ведь тогда платеж от участия положителен, если и только если противник сотрудничает.

Описание хода «иное» и платежей «выход из игры» несколько изменяется в различных изложениях опциональной ДЗ. Для Китчера они зачастую представляют собой выбор «действовать самостоятельно». Например, бабуин вместо полного или небрежного ухода за партнером в обмен на то, чтобы получить от него полный или небрежный уход, может захотеть ухаживать за собой самостоятельно. С другой стороны, зачастую предполагается, что N означает выбор «отсидеть» игру, возможно, с тем чтобы получить более подходящего партнера, с которым можно будет сыграть позже. Значимость этого различия, если она есть, затем даст о себе знать в итерационных и эволюционных версиях игры. (См. разделы 11–17 ниже.) Те, кто пишет о опциональной ДЗ, нередко выражают надежду, что она могла бы предоставить подходящую модель исследования идеи, согласно которой сотрудничество может быть достигнуто, если агенты выбирают партнеров, с которыми они взаимодействуют. Эта идея смоделирована несколько по-другому и, возможно, более непосредственно в играх в социальных сетях, обсуждаемых ниже в разделе 18. Дальнейший ее разбор представлен в указанном разделе.

Орбелл и Доуз обращают особое внимание на объяснение кооперативного поведения, опирающееся на эмпирически обоснованную гипотезу, в соответствии с которой люди зачастую выстраивают ожидания относительно поведения других на знании собственного поведения и склонностей. Согласно данной гипотезе, сотрудничающий с большей вероятностью, чем предатель, будет ожидать, что и другие сотрудничают, и поэтому, если он рационален, он более склонен принять участие в опциональной ДЗ. Орбелл и Доуз показали, что если сотрудничающий с существенно более высокой вероятностью, чем предатель, будет ожидать, что его противник сотрудничает, то (при условии, что шанс сотрудничества его противника достаточно велик) он может фактически ожидать более высокую отдачу, чем предатель, в опциональной ДЗ (Orbell and Dawes 1991). Орбелл и Доуз также приводят опытные данные (1993), согласно которым участники опциональной ДЗ действительно получают более высокие средние выплаты, нежели игроки соответствующей ДЗ, в которой не имеется ходов N. Они выдвигают резонные статистические доводы в поддержку следующих гипотез: намеревающиеся сотрудничать (те, кто сотрудничает, когда должны участвовать) добиваются большего успеха в опциональной ДЗ, чем в соответствующей ДЗ; намеревающиеся предать в целом действуют хуже в опциональной ДЗ; при определенных условиях эти прибыли и потери достаточны, чтобы поставить игроков, которые собираются сотрудничать в более выгодное положение по сравнению с теми, кто намеревается предать (как могло бы быть предсказано на основании теоретических выводов предыдущей статьи); наконец, игроки, которые ожидают сотрудничества от других (как показывает их участие), руководствуются в этом соображении скорее собственной склонностью сотрудничать, а не просто наблюдениями за характером их противника. (См. ниже «Прозрачность».)

Множество игроков и трагедия общин

Большинство исследователей, которые утверждают, что ДЗ проливает свет на вопросы морали, по-видимому, полагают, что основная структура игры отражена в ситуациях, с которыми сталкиваются группы большего размера, возможно, целые сообщества. Самое очевидное обобщение игры с двумя игроками до игры со многими игроками выплатило бы каждому игроку R, если все сотрудничают, P, если все предают, а если бы некоторые сотрудничали и некоторые предали, то S сотрудничающим и T предателям. Однако весьма маловероятно, что мы часто сталкиваемся с ситуациями, имеющими подобную структуру.

Принято считать, что структура ДЗ со многими игроками отражена в т.н. «трагедии общин», известной благодаря Гаррету Хардину*. Каждый член группы соседствующих фермеров предпочитает разрешать своей корове пастись на общинной земле вместо того, чтобы держать ее на собственной не слишком пригодной земле; однако общинная земля будет сочтена неподходящей для выпаса, если будет использоваться количеством людей, превышающим некоторое пороговое число.

Если брать шире, имеется некоторая общественная выгода B, которую каждый из участников может получить, если достаточное их число выплатит стоимость C. Платежную матрицу можно представить следующим образом:

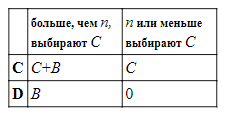
Предполагается, что стоимость C является отрицательным числом. «Искушение» здесь состоит в получении выгоды без затрат, награда — выгода с расходами, при наказании никто не совершает трату, но и не получает выгоду, а платеж простаку заключается в одной только оплате расходов без получения выгоды. Таким образом, платежи идут в порядке B>(B+C)>0>C. Как и в игре с двумя игроками, получается, что D строго доминирует C для всех игроков, а потому рациональные игроки скорее выберут D и достигнут 0, предпочитая при этом, чтобы все выбрали C и получили C+B.

В отличие от более прямого обобщения, эта матрица действительно отражает общие социальные выборы — между истощением и сохранением дефицитных ресурсов, между использованием загрязняющих и не загрязняющих окружающую среду средств производства или утилизации, а также между участием и неучастием в групповом усилии в достижении некоторой общей цели. Когда n мало, речь заходит о разновидности т.н. «дилеммы волонтера». Группа нуждается в нескольких волонтерах, при этом каждому из ее членов выгодно, чтобы волонтерами были другие. (Заметим, однако, что в истинной дилемме волонтера, где необходим только один волонтер, n равен нулю и верхний правый исход невозможен. При этих условиях D больше не доминирует C, а игра утрачивает колорит ДЗ.) Особенно раздражающее проявление этой игры возникает, когда для предотвращения вспышки смертельной болезни требуется вакцинация, чреватая серьезными побочными эффектами. Если достаточное число его соседей получает прививки, каждый человек может быть защищен, не подвергая себя риску.

Игра «трагедия общин», изображенная схематически выше, имеет несколько иные свойства по сравнению с ДЗ с двумя игроками. Прежде всего, даже если ходы каждого игрока полностью независимы от других, альтернативы, представленные колонками, уже не являются независимыми от альтернатив, представленных строками. Мой выбор C с необходимостью увеличивает вероятность того, что большее число людей, нежели n, выберет C. Чтобы гарантировать независимость, на деле мы должны изобразить матрицу в следующем виде:

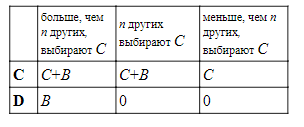
Однако теперь видно, что ход D не доминирует C. Когда мы находимся на пороге адекватного сотрудничества, где точно n других выбирают C, сотрудничество субъективно выгоднее. И все же при условии, что n является большим, представляется, будто можно пренебречь этим эффектом и из практических соображений предположить, что данная платежная матрица сходна с предыдущей.

Как мы видели в исходной ДЗ, взаимное предательство было уникальным равновесием Нэша, тогда как в этой игре имеется два схожих состояния равновесия. Одно из них — всеобщее предательство, поскольку любой игрок, отступающий от этого исхода в одностороннем порядке, будет двигаться от платежа 0 к C. В свою очередь, вторым состоянием служит минимально эффективное сотрудничество, когда количество сотрудничающих лишь незначительно превышает некий порог. Односторонне уклоняющийся от такого исхода игрок-предатель будет двигаться от B к B+C, а сотрудничающий — от B+C к 0. Отсюда можно было бы заключить, что трагедия общин менее трагична, чем ДЗ, но кажется маловероятным, что в естественных ситуациях участники будут знать, находятся ли они уже в точке равновесия минимально эффективного сотрудничества.

Кроме того, в обычной ДЗ всеобщее сотрудничество — оптимальный по Парето результат, т.е. в ней отсутствует исход, при котором каждый игрок находится как минимум в хорошем положении, а некоторые — в более выгодном. Тем не менее, в общинных играх единственные оптимальные по Парето исходы достигаются благодаря минимально эффективному сотрудничеству. Является ли при этом всеобщее сотрудничество желательным, зависит от сути рассматриваемых альтернатив. В медицинском примере может оказаться наилучшим выбором вакцинация каждого. В сельскохозяйственном примере, однако, было бы глупо запретить использовать общинную землю всем. Люди, которые избегают вакцинации, рассматриваются как «безбилетники». Недоиспользованные земли, по-видимому, выступают ярким примером «избыточного сотрудничества».

Версия игры «трагедия общин» с двумя участниками (и порогом, равным одному) порождает матрицу, которая представляет менее схожую с дилеммой ситуацию.

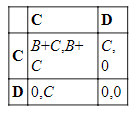
Под схему этой игры подходит пример Дэвида Юма — лодка с одним гребцом на левом борту и другим на правом (при условии, что гребцы Юма должны сделать выбор между покоем и напряжением сил одновременно друг с другом). Взаимное сотрудничество совпадает с минимально эффективным, и поэтому достигаются как равновесный, так и оптимальный по Парето результат. Игры подобной разновидноссти будут разбираться ниже под именем «охота на оленя».

Приведенные нами представления трагедии общин исходят из упрощающих допущений, в соответствии с которыми затраты и выгоды сотрудничества одинаковы для каждого игрока, расходы сотрудничества независимы от количества сотрудничающих игроков, а размер выгоды (0 или B) зависит только от того, превышает ли их число порог. В более общем описании можно заменить C и B функциями C(i,j) и B(i,j), представляющими расходы на сотрудничество игроку i, когда он является одним из ровно j сотрудничающих игроков, и выгоду, которая достается игроку i, когда ровно j игроков сотрудничают, соответственно. Мы предполагаем, что есть некоторый порог t для минимально эффективного сотрудничества, а именно такой, что B(i,j) не определена, если j>t. Мы можем также сделать следующие допущения: дополнительное сотрудничество никогда не уменьшает выгоду, которой i добивается от эффективного сотрудничества, т.е. B(i,j+1)≥B(i,j), когда j>t, а дополнительное предательство никогда не снижает расходы i на сотрудничество, т.е. C(i,j+1)≥C(i,j). Теперь вдобавок к тому предположим, что как только порог эффективного сотрудничества был превышен, расходы на сотрудничество превышают любую выгоды, которой каждый добивается от присутствия дополнительного сотрудничающего, и что затраты неэффективного сотрудничества являются истинными, т.е. для всех игроков i верно, что B(i,j)>(B(i,j+1)+C(i,j+1)), когда j больше t, и 0>C(i,j), когда j меньше или равно t. Наконец, предположим, что выгоды каждому игроку i от эффективного сотрудничества превышают затраты, т.е. для j>t верно, что B(i,j)+C(i,j)>0. В таком случае перед нами игра «трагедия общин», которая представляет знакомую дилемму: предательство выгодно игроку при любых обстоятельствах (кроме того, где точно t других сотрудничают), однако для всех лучше любое состояние эффективного сотрудничества, нежели какое-либо иное. Подобное описание можно с легкостью изменить, позволив порогу минимально эффективного сотрудничества разниться от человека к человеку (например, у i могут быть более жесткие требования к чистоте воды, чем у j) или разрешив B быть определенным всюду (тем самым устраняя порог, так что мы всегда будем извлекать выгоду из чьего-либо сотрудничества). В итоге игра по-прежнему будет иметь вид ДЗ.

Как указал Филип Петтит, примеры, которые могли бы быть представлены как ДЗ со многими участниками, разделяются на две категории. Примеры, разобранные выше, можно назвать проблемами безбилетничества. Искушение для меня состоит в том, чтобы наслаждаться выгодами, получаемыми благодаря усилиям других. Другую разновидность ДЗ со многими игроками Петтит называет проблемами грязной игры. Искушение для меня состоит в том, чтобы принести пользу себе в ущерб другим. Предположим, например, что группа людей, обладающих равной квалификацией, претендует на одну должность. Если все заполняют заявления честно, то все имеют равный шанс на найм. Если, однако, один из них солжет, то он может гарантировать себе занятость, при этом подвергаясь незначительному риску быть уличенным позднее. Если солгут все, речь снова идет о равных шансах, однако теперь каждый подвергается риску разоблачения. Таким образом, лжец-одиночка, обращая малые шансы других в ничтожные, не делает стойкими собственные малые шансы. Как отмечает Петтит, когда минимально эффективный уровень сотрудничества включает в себя весь контингент, возможности для безбилетничества нет (всеобщее сотрудничество необходимо). Таким образом, ДЗ должна принадлежать к разновидности проблем грязной игры. Но (несмотря на заявление Петтита об обратном) отнюдь не все ДЗ с грязной игрой обладают подобными характеристиками. Теперь предположим, что в истории выше речь идет о найме двух человек. Тогда все получат выгоду (шанс на занятость без риска разоблачения), если двое или более игроков не лгут. Тем не менее, лжецы представляются скорее грязными игроками, а не безбилетниками. Лучшее описание дилеммы грязной игры могло бы быть таким: каждый отказ от сотрудничества в целом сильно снижает платежи сотрудничающих, т.е. для каждого игрока i и каждого числа игроков j, превышающего порог, верно, что B(i,j+1)+C(i,j+1)>B(i,j)+C(i,j). Отказ безбилетника приносит ему выгоду, но сам по себе не наносит ущерба сотрудничающим. Отказ грязного игрока приносит ему выгоду и наносит ущерб сотрудничающим.

Игра, обозначенная ДЗ со многими участниками (см. Шеллинг 2016, Molander 1992 и др.), требует, чтобы платеж каждого сотрудничающего и отказывающегося увеличивался в строгом соответствии с количеством сотрудничающих и чтобы сумма платежей для всех сторон росла с числом сотрудничающих (так что переход одной стороны от отказа к сотрудничеству всегда бы увеличивал сумму). Ни одно из указанных условий не выполняется в изложении и примерах, разобранных выше. Они могут, однако, соблюдаться «локально», т.е. для j, близкого к порогу t для минимально эффективного сотрудничества, можно разумно предположить, что:

 — для каждого человека i верно, что B(i,j+1)+C(i,j+1)>B(i,j)+C(i,j) при j>t,

 — для каждого человека i верно, что C(i,j+1)>C(i,j) при j≤t и 

B(1,j+1)+C(1,j+1)+…+B(j+1,j+1)+C(t+1,j+1)+B(j+2,j+1))+…+B(n,j+1) >B(1,j)+C(1,j)+…+B(j,j)+C(j,j)+B(j+1,j)+…+B(n,j). 

Требуя в своих изложениях ДЗ с n игроками, чтобы сотрудничество других всегда приносило выгоду всем и каждому, Шеллинг и Моландер оказываются не в состоянии смоделировать избыточное сотрудничество / явление безбилетника, которые определяют ситуации по типу трагедии общин. Их параметры могли бы, тем не менее, служить правдоподобной моделью некоторых дилемм общего блага. Вполне разумно было бы предположить, что любой вклад в здравоохранение, оборону страны, безопасность дорожного движения или предотвращение загрязнения воздуха ценен для всех независимо от того, сколько вкладов уже было сделано, и что расходы каждого человека на его вклад в достижение таких благ при этом всегда превышают получаемую им выгоду. Подобная перспектива имеет преимущество, поскольку делает упор на дилемматичность игры. Отказ доминирует сотрудничество, в то время как всеобщее сотрудничество единодушно предпочитается всеобщему отказу. Майкл Тэйлор заходит в этом направлении еще дальше. Его версия ДЗ со многими участниками требует соблюдения лишь упомянутых только что двух условий ДЗ и одного дополнительного, в соответствии с которым отказывающимся всегда лучше, когда кто-либо сотрудничает, чем тогда, когда никто этого не делает. (Основным предметом внимания Тэйлора является итеративная разновидность этой игры, которая будет разобрана в дальнейших редакциях этой статьи.)

Версии с одним участником

Обычно считается, что ДЗ наглядно представляет конфликт между индивидуальной и коллективной рациональностью, однако версия ДЗ со многими игроками (или кое-что очень похожее на нее) рассматривалась также как демонстрация затруднений, с которыми сталкиваются стандартные концепции индивидуальной рациональности. Одна из таких трактовок (Quinn 1990) опирается на пример Дерека Парфита. Медицинское устройство позволяет электрическому току воздействовать на тело пациента в приращениях настолько незначительных, что разницу между смежными настройками нельзя заметить. Вы прикреплены к такому устройству. Раз в день на протяжении десяти лет вы можете изменить одну настройку устройства и при этом накопить тысячу долларов либо оставить ее как есть и не получить ничего. Поскольку разницу между смежными настройками заметить нельзя, то, по всей видимости, рационально было бы изменять настройку каждый день. Но по истечении десяти лет боль стала бы настолько сильной, что рациональный человек пожертвовал бы всем своим богатством, чтобы возвратиться к первой настройке.

Мы можем рассмотреть данную ситуацию как ДЗ со многими игроками, в рамках которой «игроками» оказываются состояния одного и того же человека, разнесенные по времени. Понимаемая таким образом, ситуация обладает как минимум двумя характеристиками, которые не обсуждались ранее в связи с ДЗ того же типа. Во-первых, ходы игроков являются последовательными, а не одновременными (и каждый из них имеет сведения о предшествующих ходах). Во-вторых, имеется свойство, связанное с градацией. Увеличение электрического тока от одной настройки к следующей является незаметным, и поэтому незначительным для рационального принятия решения, но в совокупности прирастания тока заметны и имеют огромное значение. Тем не менее, ни одна из указанных характеристик не является специфической для примеров с одним человеком. Так, рассмотрим выбор между загрязняющими и не загрязняющими окружающую среду средствами утилизации отходов. Каждый житель из домов на берегу озера может выбросить мусор в озеро или использовать менее удобное закапывание мусора. Разумно предположить, что каждый действует с пониманием того, как прежде действовали другие. (См. «Асинхронные ходы» ниже.) Также разумно предположить, что выбрасывание одной банки в озеро не влияет на качество воды сколь-либо заметным образом, а следовательно, не оказывает воздействия на благосостояние жителей. Тот факт, что речь по-прежнему идет о дилемме, означает, что схожие с ДЗ ситуации порой вовлекают нечто большее, чем конфликт между индивидуальной и коллективной рациональностью. В примере с одним участником осознание нами того, что мы заботимся скорее о своем итоговом самочувствии, нежели об отдельных временных состояниях, (само по себе) не устраняет аргумент, в соответствии с которым рациональнее продолжить изменять настройку. Точно так же одно лишь решение позволить коллективной рациональности одержать верх над индивидуальной в примере с загрязнениями не отводит аргумент в пользу сброса отходов. Тем не менее, было бы уместно отделить эту проблему от поднимаемых в обычных ДЗ. Градации, которые являются незаметными по отдельности, но существенными в целом, порождают интранзитивные предпочтения. Это вызов стандартным теориям рациональности, и неважно, возникает он в ДЗ (либо сходных с ДЗ ситуациях) или нет.

Вторая трактовка ДЗ, рассматривающая ее как игру с одним участником, предлагается Кавкой (Kavka 1991). В соответствии с ней заключенные являются не различными временными состояниями, а скорее «субагентами», отражающими различные пожелания, которыми я мог бы руководстваться при принятии решения. Представьте, что я голоден и собираюсь приобрести еду. У меня есть четыре варианта:

a. Купить шарик шоколадного желе.

b. Купить шарик апельсинового шербета.

c. Купить батончик мюсли.

d. Не купить ничего.

Сторона моей личности, пекущаяся о здоровье, назовем ее «Арнольд», располагает варианты в следующем порядке: c, b, d, a. Любящая же вкусности сторона, «Эппи», упорядочивает их так: a, b, d, c. Подобный внутренний конфликт предпочтений зачастую разрешается способами, совместимыми с стандартными представлениями об индивидуальном выборе. Мой итоговый порядок предпочтений, к примеру, можно определить посредством взвешенного среднего значения предпочтений, которые Арнольд и Эппи присваивают каждому из вариантов. Также вполне возможно, предполагает Кавка, что разрешение моих внутренних конфликтов подобно результату стратегического взаимодействия среди рациональных субагентов. В этом случае Арнольд и Эппи каждый могут либо настоять (insist) на своем (I), либо согласиться (acquisce) на компромисс (A). Взаимодействие между субагентами тогда можно представить в виде следующей платежной матрице, где Арнольд играет cтроку, а Эппи — cтолбец.

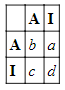
Рассмотрение таблицы и упорядочений предпочтений подтверждает, что перед нами снова внутриличностная ДЗ. Кавка утверждает, что такая история могла бы «предоставить нам правдоподобную в психологическом отношении картину того, как внутренний конфликт может привести к неоптимальному действию». Тем самым также подрывается стандартное воззрение, согласно которому выборы отражают ценности: скорее, они частично отражают «структуру внутреннего конфликта».

Количественные платежи

Если игра определяет абсолютный (в противоположность относительному) платеж, то всеобщее сотрудничество может и не привести к оптимальному по Парето исходу даже в ДЗ с двумя участниками. Поскольку при некоторых условиях оба игрока добиваются большего успеха, придерживаясь смешанной стратегии сотрудничества с вероятностью p и отказа от него с вероятностью (1−p). Этот момент представлен на графиках ниже.

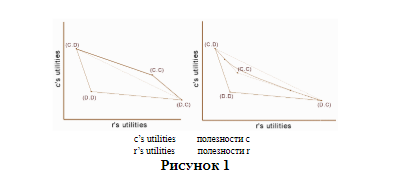
Здесь оси x и y отражают полезности Ряда (r) и Колонки (c). Четыре исхода, вписанные в матрицу второго раздела, представлены обозначенными точками. Условия PD3a и 3b гарантируют, что (C,D) и (D,C) лежат к северо-западу и к юго-востоку от (D,D), а PD3c, в свою очередь, отражено в том обстоятельстве, что (C,C) лежит к северо-востоку от (D,D). Предположим сначала, что (D,D) и (C,C) лежат на противоположных концах линии между (C,D) и (D,C), как на графике слева. Тогда четыре точки формируют выпуклый четырехугольник, и платежи допустимых исходов смешанных стратегий представлены всеми точками в пределах этого четырехугольника. Конечно, в действительности игрок может только получить один из четырех возможных платежей всякий раз, когда играет, но точки в четырехугольнике представляют ожидаемые стоимости платежей двух игроков. Если Ряд и Колонка сотрудничают с вероятностями p и q (и отказываются от сотрудничества с вероятностями p*=1−p и q*=1−q), тогда ожидаемая стоимость платежа Ряда равна p*qT+pqR+p*q*P+pq*S. Рациональный эгоистичный игрок, согласно стандартным теориям, должен предпочесть более высокий ожидаемый платеж более низкому. На графике слева платеж всеобщего сотрудничества (с вероятностью один) оптимален по Парето среди платежей всех смешанных стратегий. На графике справа, однако, где и (D,D), и (C,C) лежат к юго-западу от линии между (C,D) и (D,C), все устроено сложнее. Здесь платежи допустимых исходов лежат в пределах фигуры, ограниченной на северо-востоке тремя различными отрезками кривой (двумя линейными и одним вогнутым). Заметьте, что (C,C) находится теперь на участке области, ограниченной сплошными линиями, а это значит, что имеются смешанные стратегии, которые обеспечивают обоим игрокам более высокий ожидаемый платеж, чем (C,C). Важно отметить, что здесь мы говорим о независимых смешанных стратегиях. Ряд и Колонка используют частные рандомизирующие устройства и никак не коммуницируют. Если бы они были в состоянии скоррелировать свои смешанные стратегии, чтобы гарантировать (C,D) с вероятностью p и (D,C) с вероятностью p*, множество допустимых решений простиралось бы до пунктира между (C,D) и (D,C) включительно. Дело в том, что, даже если ограничить наше рассмотрение играми с независимыми стратегиями, удовлетворяющим перечню условий PD3, среди них есть такие, в которых оба игрока могут добиться большего успеха, чем при всеобщем сотрудничестве. ДЗ, в которой всеобщее сотрудничество является оптимальным по Парето, можно назвать чистой ДЗ. (Это явление зафиксировано в Kuhn and Moresi 1995 и применено к моральной философии в Kuhn 1996.) Чистая ДЗ характеризуется добавлением к перечню PD3 следующего условия:

(P)      (Tr−Rr)(Tc−Rc)≤(Rr−Sr)(Rc−Sc)

В симметричной игре P сводится к более простому условию

(RCA) R≥(T+S)

(названному в честь авторов Рапопорта, Чамма и Аксельрода, которые впервые его применили).

ДЗ с точными копиями и каузальная теория принятия решений

Один спорный аргумент, в соответствии с которым в ДЗ рациональнее сотрудничать, полагается на наблюдение, что мой партнер по преступлению, вероятно, будет думать и действовать во многом как я. (См., например, Davis 1977 и 1985, где этот аргумент излагается в позитивном ключе, и Binmore 1994: ch. 3.4–3.5, где он переформулируется и тщательно опровергается.) В экстремальном случае мой сообщник — точная копия меня, которая мыслит так же, как я — так что мы с необходимостью поступили бы одинаково. В таком случае можно было бы посчитать, будто возможных исходов всего два — либо оба игрока сотрудничают, либо оба предают. Так как платеж награды превышает платеж наказания, мне следует сотрудничать. Если брать шире, даже если мой сообщник не является идеальной копией меня, вероятность его сотрудничества больше, если я сотрудничаю, а отказа — больше, если я предаю. Когда корреляция между нашими поведениями достаточно сильна или разница платежей достаточно велика, мой ожидаемый платеж (в привычном понимании термина) выше в том случае, если я сотрудничаю, а не предаю. Контраргумент, безусловно, состоит в том, что мое действие каузально (т.е. причинно) независимо от поступка моей точной копии. Так как я не могу повлиять на действия моего сообщника и поскольку, независимо от того, что он делает, мой платеж оказывается больше, если я предаю, я должен отказываться от сотрудничества. Эти аргументы во многом схожи с доводами двух позиций относительно парадокса Ньюкома. (Данная головоломка стала известной среди философов благодаря статье Nozick 1969. Степень сходства явно обозначена в Lewis 1979). Парадокс Ньюкома предлагает рассмотреть две коробки, одну прозрачную и одну непрозрачную. В прозрачной коробке мы можем видеть тысячу долларов. Непрозрачная коробка либо содержит миллион долларов, либо пуста. У нас есть два варианта: выбрать непрозрачную коробку с ее содержимым либо обе. Мы знаем перед принятием решения, что надежный предсказатель нашего поведения поместил бы миллион долларов в непрозрачную коробку, если бы предсказал, что мы взяли ее, и оставил бы ее пустой, если бы предсказал, что мы взяли обе. Чтобы понять, как именно каждый участник ДЗ сталкивается с парадоксом Ньюкома, рассмотрите следующую платежную матрицу.

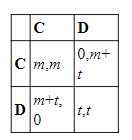
«Сотрудничая» (выбирая непрозрачную коробку), каждый игрок гарантирует, что другой получает миллион долларов (еще тысячу в случае предательства). Решив «предать» (выбрать обе коробки), каждый игрок гарантирует, что он получит тысячу долларов сам по себе (плюс еще миллион, если другие сотрудничают). Пока m>t>0, структура этой игры соответствует обычной ДЗ с двумя игроками и двумя ходами (и любая такая ДЗ может быть представлена в этом виде). Кроме того, аргументы в пользу «одной коробки» и «двух коробок» в обсуждениях парадокса Ньюкомба совпадают с доводами в пользу сотрудничества и предательства при разборе дилеммы заключенного, где есть положительная корреляция между ходами игроков. Две коробки — доминирующая стратегия: две коробки выгоднее, чем одна, полна она или нет. С другой стороны, если предсказатель надежен, ожидаемый платеж для одной коробки больше, чем для двух. [Однако см. Hurley 1991, где утверждаются существенные различия между двумя головоломками. В ДЗ (будь то обычной или же ньюкомовской разновидности) каждый игрок знает, что другой рационален и что тот ранжирует исходы ранее описанными способами. Согласно Хёрли, тем самым раскрывается возможность для совместного действия, которая отсутствует в исходного парадокса Ньюкома.]

Интуиция, согласно которой рациональным выбором в парадоксе Ньюкома (ДЗ с положительной корреляцией ходов игроков) является предпочтение двух коробок (предательство), кажется, вступает в разногласие с идеей, что рациональность требует максимизации ожиданий. Этот очевидный конфликт привел к предположению, что стандартная теория принятия решений должна быть усовершенствована для рассмотрения случаев, в которых действия агента предоставляют сведения о контексте, в котором он действует, без того, чтобы воздействовать на него каузально. В случае ДЗ стандартная теория принятия решений (эвиденциальная, т.е. опирающаяся на сведения) требует, чтобы первый игрок сравнил свои ожидаемые полезности сотрудничества и отказа от него, которые могут быть обозначены как p(C2∣C1)×R+p(D2∣C1)×S и p(C2∣D1)×T+p(D2∣D1)×P (где, например, p(C2∣C1) является условной вероятностью, что второй игрок сотрудничает, если сотрудничает первый). Если ходы игроков жестко скоррелированы, тогда p(C2∣C1) и p(D2∣D1) будут близки к единице, а p(C2∣D1) и p(D2∣C1) — к нулю. В рамках предложенных исправлений эти условные вероятности следует заменить некоторой разновидностью каузально-условных вероятностей, которые могли бы (в некоторых изложениях) быть выраженными такими фразами, как «вероятность, что второй также сотрудничал бы, если бы стал сотрудничать первый». Когда ходы каузально независимы, речь идет лишь о вероятности сотрудничества второго.

Довольно неправдоподобный сценарий, описанный в парадоксе Ньюкома, первоначально заставил некоторых сомневаться относительно значимости различия между каузальной и эвиденциальной теориями принятия решений. Согласно Дэвиду Льюису, связь с ДЗ предполагает, что ситуации, где два решения расходятся, не столь уж редки, и недавние публикации, посвященные каузальной теории принятия решений, содержат много куда менее причудливых примеров, нежели парадокс Ньюкома. (См., напр., Joyce 1999.)

Можно отметить, что рассматриваемая здесь «ДЗ с точными копиями» в литературе обычно именуется «ДЗ с близнецами». Один из доводов в пользу используемого здесь названия состоит в том, чтобы нам следует отличать эти идеи от сообщений об экспериментах, в которых настоящие (одно- или двуяйцевые) близнецы играли в ДЗ. (См., напр., Segal and Hershberger 1999.) Оказывается, что близнецы и правда с большей вероятностью сотрудничают в ДЗ, чем незнакомцы, однако нет никаких свидетельств, указывающих на то, что они руководствуются при этом спорными доводами, изложенными выше.

Охота на оленя и ДЗ

Во введении было упомянуто, что, по мнению некоторых исследователей, ДЗ моделирует проблемы сотрудничества среди рациональных агентов. Подобный взгляд иногда критикуется, поскольку в истинной ДЗ кооперативный результат не совпадает с равновесием Нэша. Любая «проблема» подобного характера, настаивают критики, будет неразрешимой. (См., напр., Sugden 1986 или Binmore 2005: ch. 4.5.) Слегка изменив структуру платежей ДЗ так, чтобы награда превысила искушение, мы получим игру, где обоюдное сотрудничество, равно как и предательство, являются равновесием Нэша. Такая игра известна как «охота на оленя». Она могла бы предоставить более выгодную модель для ситуаций, где сотрудничать затруднительно, но все еще возможно. Также она могла бы подойти для описания других ролей, иногда назначаемых ДЗ. Если говорить более конкретно, охота на оленя — это игра с двумя игроками и двумя ходами; ее платежная матрица сходна с матрицей ДЗ, изображенной выше, где условия PD1 заменены: 

(SH)

a. R>T

b. R>P

c. P>S

Драматическая фабула игры, давшая ей название, взята из «Рассуждения о происхождении неравенства» Жан-Жака Руссо (Руссо 1969: 75). Речь идет об охотничьем походе, а не дознании обитателей тюремной камеры. Два охотника надеются добыть оленя. Успех весьма сомнителен и для своего достижения требует усилий обоих. Тем не менее, любой охотник может оставить партнера и поймать зайца с хорошим шансом на успех. Типичная платежная матрица показана ниже.

Здесь «сотрудничеством» является участие в охоте на оленя с партнером, «предательство» же состоит в охоте на зайца. Платеж «искушения» в охоте на оленя уже не слишком соблазнителен, но мы сохраняем терминологию для простоты описания. В этом случае искушение и штрафы наказания совпадают друг с другом, возможно, отражая то обстоятельство, что выбор моего партнера по добыче не оказывает никакого воздействия на мой успех в охоте на зайца. В другом варианте можно говорить об искушении, которое превышает наказание, по-видимому, поскольку охота на зайца оказывается более полезной, когда проводится совместно, а не поодиночке (хотя все еще менее полезной, разумеется, чем совместная охота на оленя), или о наказании, превышающем искушение, поскольку второй охотник на зайца вступает в бесполезное соревнование. В любой случае суть охоты на оленя остается неизменной. Есть два равновесия, одно единодушно предпочтительнее другого. Охота на оленя становится «дилеммой», когда рациональность требует от обоих игроков выбрать действие, приводящее к низшему равновесию. Само собой, если я уверен, что партнер будет охотиться на оленя, я должен присоединиться к нему, а если я уверен, что он будет охотиться на зайца, я должен поступить так же. По этой причине игры с подобной структурой иногда называют «играми на координацию» или «играми на доверие». Если я не знаю, какие действия предпримет мой партнер, в соответствии со стандартной теорией принятия решений мне следует максимизировать ожидание. А значит, мне нужно неким образом оценить вероятность того, что партнер сделает ход C или D. Если же мне недостает информации для какой бы то ни было оценки, то в соответствии с предполагаемым принципом рациональности («безразличием») я должен рассмотреть все варианты как одинаково вероятные. Согласно данному критерию, мне следует охотиться на зайца, если и только если выполняется следующее условие:

— (SHD) T+P>R+S

Когда SHD имеет место, говорится, что охота на зайца является «доминирующим по риску» равновесием. Будем называть игру «охота на оленя», где выполняется данное условие, дилеммой охоты на оленя (SHD). Матрица, приведенная выше, иллюстрирует один пример.

Другой выдвинутый принцип рациональности («максимин») предполагает, что мне следует рассмотреть наихудший платеж, который я смог бы получить при любом образе действий, и выбрать то действие, которое максимизирует это значение. Так как платеж простаку — худший в охоте на оленя, в соответствии с указанным принципом любая охота на оленя представляет дилемму. Максимин, однако, более пригоден в качестве принципа рациональности для игр с нулевой суммой, где можно допустить, что рациональный противник попробует минимизировать мой счет, чем для игр наподобие охоты на оленя, где рациональный противник будет рад видеть, что я преуспеваю, пока преуспевает он сам.

Охота на оленя может быть обобщена очевидным способом для согласования асимметричных и кардинальных (количественных) платежей. Четырехугольник, образуемый в графическом представлении игр, является выпуклым, а потому различие чистое/нечистое более не применимо. (Другими словами, в охоте на оленя никакие смешанные стратегии не могут предпочитаться взаимному сотрудничеству.) Самый очевидный способ обобщить игру для многих игроков сохранил бы условие, в соответствии с которым должно иметься ровно два равновесия, причем одно из них однозначно предпочтительнее другого. Это могло бы быть хорошей моделью для кооперативной деятельности, в которой успех требует полного сотрудничества. Представим себе, к примеру, что единственный загрязнитель может испортить озеро или единственная утечка — помешать расследованию. Если вовлекается множество агентов и вследствие безразличия или по другим причинам мы оцениваем вероятность, что они будут сотрудничать, в 50%, то эти примеры представляли бы дилеммы охоты на оленя в экстремальной виде. Каждый извлек бы выгоду при всеобщем сотрудничестве, но только очень доверчивый и недалекий человек будет считать, что именно в этом состоит рациональный повод для его непосредственного сотрудничества. Возможно, более широкое обобщение до ситуации со многими участниками представило бы структуру других знакомых нам социальных явлений, однако распространяться на данную тему мы здесь не будем.

Кооперативный исход в охоте на оленя может быть гарантирован многими из средств, уже разобранных нами ранее в контексте ДЗ. Как можно было ожидать, в охоте на оленя с двумя участниками обеспечить сотрудничество несколько легче, чем в ДЗ с двумя участниками. (Мы не будем здесь вдаваться в подробности, однако посоветуем заинтересованному читателю обратиться к работе Skyrms 2004, ответственной за недавний всплеск интереса к этой игре.)

Асинхронные ходы

Зачастую утверждалось, что рациональные эгоистичные игроки могут прийти к кооперативному результату, делая свои ходы с оглядкой на ходы другого игрока. Питер Дэниелсон, в частности, одобряет стратегию взаимного сотрудничества: если другой игрок сотрудничал бы, если вы сотрудничаете, и предавал, если вы этого не делаете, так сотрудничайте, но в противном случае предавайте. Подобные условные стратегии исключены в версиях описанной выше игры, однако могут быть применены в версиях, которые более точно моделируют жизненные ситуации. В настоящем и следующем разделах мы разбираем две таких версии. В этом разделе мы устраняем требование, чтобы два игрока делали ходы одновременно. Возьмем, к примеру, ситуацию фирмы, единственный конкурент которой только что снизил цены. Или предположим, что покупатель автомобиля только что заплатил согласованную покупную цену, а продавец еще не передал право на владение собственностью. Мы можем рассуждать об этих случаях как о ситуациях, в которых один игрок должен сделать выбор: сотрудничать или отказываться от сотрудничества после того, как другой игрок уже сделал подобный выбор. Соответствующая игра называется асинхронной или расширенной ДЗ.

Пример асинхронной ДЗ, как недавно отметили Скирмс (Skyrms 1998) и Вандерскраф (Vanderschraaf 1998), был подвергнут тщательному разбору в сочинениях Дэвида Юма задолго до того, как Флуд и Дрешер описали структуру обычной ДЗ. Юм пишет о двух соседствующих друг с другом фермерах-хлеборобах:

Ваша рожь поспела сегодня; моя будет готова завтра; для нас обоих выгодно, чтобы я работал с вами сегодня и чтобы вы помогли мне завтра. Но у меня нет расположения к вам, и я знаю, что вы также мало расположены ко мне. Поэтому ради вас я не возьму на себя лишней работы, а если бы я стал помогать вам ради себя самого в ожидании ответной услуги, то знаю, что меня постигло бы разочарование и что я напрасно стал бы рассчитывать на вашу благодарность. Итак, я предоставляю вам работать в одиночку; вы отвечаете мне тем же; погода меняется; и мы оба лишаемся урожая вследствие недостатка во взаимном доверии и невозможности рассчитывать друг на друга. (Юм 1996: 560)

Из уважения к Юму Скирмс и Вандерскраф именуют данный вид асинхронной ДЗ «дилеммой фермера». Ее можно наглядно представить с помощью древовидной диаграммы.

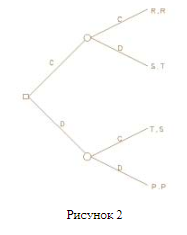
Время на ней течет слева направо. Узел, отмеченный квадратом, указывает точку выбора первого игрока; отмеченные кругами указывают выборы второго. Ходы и платежи каждого игрока точно такие же, что и в обычной ДЗ, но здесь второй игрок может сделать ход с оглядкой на ход первого. Древовидные диаграммы подобного вида являются развернутой формой представления игры, тогда как приведенные ранее платежные матрицы являются нормальной формой представления. Как показывает анализ Юма, если игру сделать асинхронной, дилемма не исчезает. Первый игрок знает, что если он выберет C на первом ходу, второй выберет D на втором (поскольку предпочитает искушение награде), так что самому первому игроку достанется платеж простака. Если же первый игрок выберет D, второй все равно выберет D (поскольку предпочитает наказание платежу простака), и первый игрок закончит с платежом наказания. Поскольку он предпочитает платеж наказания платежу простака, первый игрок выберет D на первом ходу, и в итоге оба получат платеж наказания. Такой вид «обратного» рассуждения, в рамках которого игроки сначала оценивают результат последнего хода при реализации различных игровых историй, а затем определяют, что произойдет на предшествующих ходах, достаточно широко применяется к играм в развернутой форме, а обобщенный вариант подобного подхода будет рассмотрен далее под названием конечная итерация.

При представлении дилеммы фермера в нормальной форме первый игрок считается выбирающим между C и D, а второй — выбирающим сразу между четырьмя условными ходами: безусловным сотрудничеством (Cu), безусловным отказом (Du), копированием хода первого игрока (I) и совершением противоположного хода (O). В итоге речь идет об игре с двумя участниками и со следующей матрицей.

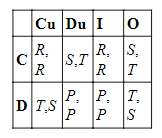
Читатель может заметить, что эта игра представляет собой (многоходовую) равновесную дилемму. Единственное (слабое) равновесие Нэша имеет место в том случае, когда первый игрок выбирает D и второй играк выбирает Du, тем самым получая наиболее низкие платежи P и P. Игра, однако, не является доминирующей ДЗ. Действительно, ни у одного из игроков нет никакого доминирующего хода. Обычно считается, что рациональные эгоистичные игроки достигнут равновесия Нэша, даже если ни один из них не обладает доминирующим ходом. Если это верно, дилемма фермера по-прежнему остается дилеммой.

Для сохранения симметрии между игроками, которая свойственна обычной ДЗ, мы могли бы захотеть изменить асинхронную игру. Пусть расширенная ДЗ играется поэтапно. Сначала каждый игрок выбирает первый (C или D) и второй ходы (Cu,Du,I или O). Затем рефери определяет, кто делает ход первым, давая каждому игроку равный шанс. Наконец, надлежащим образом вычисляется исход. Например, предположим, что Ряд играет (D,O) (откажется от сотрудничества, если совершит ход первым, и сделает противоположный своему противнику ход, если сыграет вторым), а Колонка играет (C,Du). Тогда Ряд получит P, если пойдет первым, и T, если вторым, а значит, его ожидаемый платеж равен (P+T). Колонка получит S, если совершит ход первой, и P, если второй, и потому ее ожидаемый платеж равен (P+S). Это прямой, хотя утомительный способ рассчитать все платежи матрицы размером 8х8. После выполнения этой операции читатель может заметить, что, подобно дилемме фермера, симметричная форма расширенной ДЗ является равновесной, но не доминирующей. Единственное равновесие Нэша возникает, когда оба игрока следуют стратегии (D,Du), получая в конечном итоге самые низкие платежи (P,P).

Стоит отметить, что асинхронная версия охоты на оленя представляет незначительный интерес по сравнению с ДЗ. Если первый игрок вносит свой вклад в охоту на оленя в первый день, второму следует внести свой вклад во второй день. Если он охотится на зайца в первый день, то должен поступить так же во второй день. Первый игрок, понимая это, станет охотиться на оленя в первый день. Таким образом, рациональные игроки без особых затруднений достигнут кооперативного исхода в асинхронной охоте на оленя.

Прозрачность

Другой способ ввода условных ходов в ДЗ опирается на предположение, что игроки обладают свойством, которое Дэвид Готье назвал прозрачностью. Полностью прозрачным является игрок, намерения которого видны другим целиком. Никто не считает, что люди являются полностью прозрачными, но наблюдение, что мы часто можем успешно предсказывать действия других, предполагает, что мы по меньшей мере «просвечиваем». Кроме того, агенты большего масштаба, такие как фирмы или страны, которые могут публично обсуждать образ будущих действий, оказываются более прозрачными, чем мы. А значит, исследования ДЗ с прозрачными игроками представляют теоретический интерес. Предположительно такие игроки могут реализовать условные стратегии, превосходящие по сложности стратегии (непрозрачных) расширенных игроков: к примеру, стратегии, обусловленные чужими условными стратегиями. Однако трудно с точностью определить, какие стратегии являются выполнимыми или допустимыми для таких игроков. Предположим, что Ряд принял стратегию «делаю то же, что и Колонка», а Колонка следует стратегии «поступаю не как Ряд». Данные стратегии никоим образом нельзя осуществить одновременно. С другой стороны, если каждый придерживается стратегии «подражаю другому игроку», есть два способа, посредством которых стратегии можно реализовать, но при этом нельзя определить, какой из них будет претворен в жизнь. Найджел Ховард —вероятно, первый, кто подверг такие условные стратегии систематическому разбору — избегал этого затруднения, настаивая на строго типизированной иерархии игр. На базовом уровне мы имеем обычную ДЗ, где каждый игрок выбирает между C и D. Для любой игры G в иерархии мы можем произвести две новых игры RG и CG. В RG Колонка совершает те же ходы, что в игре G, а Ряд может выбрать любую функцию, которая приписывает C или D каждому из возможных ходов Столбца. Схожим образом в CG Ряд имеет те же ходы, что в G, а Колонка располагает новым множеством условных ходов. Например, если [PD] является игрой базового уровня, то C[PD] является игрой, в которой Колонка выбирает между упоминавшимися выше стратегиями Cu, Du, I и O. Ховард отметил, что в двух трехуровневых играх RC[PD] и CR[PD] (и в каждой игре более высокого уровня) имеется равновесный исход, приносящий каждому игроку R. В частности, такое равновесие достигается, когда один игрок играет I и другой сотрудничает, если его противник играет I, и предает, если его противник играет Cu, Du или O. Заметьте, что описанная стратегия эквивалентна взаимному сотрудничеству Дэниелсона, описанному в последнем разделе.

Неясно, какие отсюда можно сделать выводы в отношении рационального действия. Предположим, что два игрока в ДЗ были достаточно прозрачными, чтобы задействовать условные стратегии высокоуровневых игр. Как они решат, в игру какого уровня играть? Кто выберет копирование хода, а кто взаимное сотрудничество? Совершить ход в высокоуровневой игре означает, по всей видимости, сформировать намерение, наблюдаемое другим игроком. Но почему какой бы то ни было игрок должен ожидать осуществления намерений, если для него может оказаться выгодным их проигнорировать?

Условные стратегии применяются более убедительно, когда мы ставить себе цель не изучить игру в ДЗ, а сконструировать агентов, способных успешно играть в ней против многих вероятных соперников. Такова точка зрения Дэниелсона. (См. также ранний полезный обзор данной позиции в J.V. Howard 1988.) Условная стратегия является не намерением, которое игрок формирует как ход в игре, но детерминистским алгоритмом, определяющим тип игрока. Действительно, один из выводов ДЗ может звучать так: прозрачные агенты преуспевают, если могут сформировать безотзывные «протоколы действия» вместо того, чтобы всегда следовать намерениям, которые у них могут образовываться во время действия. Дэниелсон не ограничивается априорно рассмотрением стратегий, находящихся в пределах иерархии Ховарда. Агентом является просто-напросто компьютерная программа, которая может содержать строки, позволяющие другим программам прочитать и исполнить их. Мы могли бы без особого труда написать две программы, каждая из которых бы определяла, сыграет ее противник C или D, и поступала противоположным образом. Ход их игры в ДЗ зависит от нюансов выполнения, но вполне вероятно, что они окажутся «несогласованными», т.е. войдут в бесконечные циклы и будут неспособны сделать какой бы то ни было ход вообще. Для того чтобы быть успешной, программа должна оказаться в состоянии совершать ходы, будучи спаренной со множеством других программ, в том числе со своими копиями, и получать ценные результаты. Программы, реализующие I и O прямым способом, вряд ли преуспеют, поскольку в паре друг с другом они будут непоследовательными. Программы, реализующие Du, вряд ли преуспеют, поскольку получают только P, оказавшись в паре со своими клонами. Реализующие Cu вряд ли преуспеют, потому что получают только S в соединении с программами, которые распознают и эксплуатируют их безусловно кооперативный характер. Критерии успеха достаточно туманны. В схеме Ховарда можно было сравнить условную стратегию со всеми возможными альтернативами того же самого уровня. В данной же ситуации, когда любые две программы могут быть соединены, такой подход является бессмысленным. Однако некоторые программы, по всей видимости, преуспевают, оказываясь в паре с широким разнообразием игроков. Одна из них является версией стратегии, которую Готье продвигал под названием ограниченной максимизации. Идея состоит в том, что игрок j должен сотрудничать, если другой сотрудничал бы, если j так поступил, а иначе отказаться от сотрудничества. 

Заявляется, что эта стратегия подходит для игр RC[PD] или CR[PD]. Не вполне ясно, как придерживающаяся ее программа совершала бы ходы (и ходила бы вообще) в парном соединении с самой собой. Дэниелсон сумел выстроить приближение к ограниченной максимизации, однако оно сотрудничает с собой. Программа Дэниелсона (и другие реализации ограниченной максимизации) не может быть согласованным образом соединена со всеми структурами. Однако она действительно совершает ходы и показывает хороший результат, сталкиваясь с известными стратегиями. Она сотрудничает с Cu и с собой и предает Du. Если она соединена согласованным образом, то представляется гарантируемым платеж не хуже P.

Вторая успешная программа моделирует взаимное сотрудничество Дэниелсона. Опять же, не вполне ясно, как стратегия (как сформулировано выше) допускает сотрудничество (или прочий ход) с собой, но Дэниелсон в состоянии выстроить аппроксимацию, которая способна к этому. (Приблизительное) взаимное сотрудничество преуспевает в той же мере, что и (приблизительная) ограниченная максимизация, выступая против себя, Du и ограниченной максимизации. Против Cu оно выступает даже лучше, получая T, в то время как ограниченная максимизация получает только R.

Конечная итерация

Многие из ситуаций, которые предположительно имеют структуру ДЗ — такие как ассигнования соперничающих держав на военные расходы или регулировка цен дуополистических фирм — лучше моделируются итеративной версией игры, в которой игроки играют в ДЗ неоднократно, сохраняя доступ в каждом раунде к исходам всех предыдущих. В этих итеративных ДЗ (далее ИДЗ) игроки, которые отказались от сотрудничества в одном раунде, могут быть «наказаны» предательствами в последующих раундах, а сотрудничающие могут быть вознаграждены сотрудничеством. Таким образом, надлежащая стратегия для рационально эгоистичных игроков более не очевидна. Теоретический ответ, как оказывается, во многом зависит от определения задействованной ИДЗ и знания, приписанного рациональным игрокам.

ИДЗ может быть представлена в виде обширной древовидной схемы, подобной рассмотренной выше для дилеммы фермера.

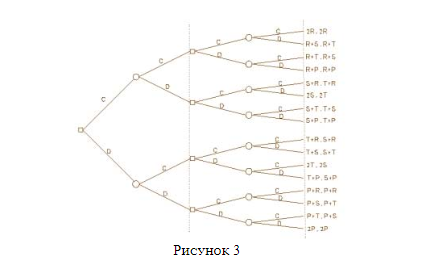
Здесь мы имеем ИДЗ длиной в два раунда. Конец каждого из них отмечен пунктирной вертикальной линией. Платежи каждого из двух игроков (полученные сложением их платежей за два раунда) указаны в конце каждого пути через дерево. Это наглядное представление отличается от предыдущего тем, что два узла на каждой ветви в пределах того же самого деления обозначают одновременные выборы двух игроков. Так как ни один из игроков не знает ход другого в том же самом раунде, ИДЗ никак не может называться одной из «игр с полной информацией», привычных для теоретиков игр. Если игроки совершают ходы последовательно, а не одновременно (что мы могли бы указать, удалив пунктирные вертикальные линии), мы имели бы дело с итеративной дилеммой фермера, которая действительно отвечает привычному теоретико-игровому определению и разделяет многие из функций, делающих ИДЗ интересной.

Подобно дилемме фермера, ИДЗ теоретически может быть представлена в нормальной форме, где ходы игроков становятся стратегиями, сообщающими им, как совершать ходы, если им нужно достичь какого-либо узла в конце раунда игрового дерева. Число стратегий очень быстро растет вместе с длиной игры таким образом, что на деле становится невозможным выписать нормальную форму для всех ИДЗ, кроме самой короткой. Каждая пара стратегий определяет «процесс» игры, т.е. путь через дерево развернутой формы.

В подобной игре понятие равновесия Нэша отчасти теряет свой привилегированный статус. Вспомните, что пара ходов ведет к равновесию Нэша, если каждый из них является лучшим ответом другому. Расширим систему обозначений, используемую в обсуждении асинхронной ДЗ, и позволим Du быть стратегией, которая призывает к отказу от сотрудничества в каждом узле ИДЗ. Легко видеть, что Du и Du образуют равновесие Нэша. Но вопреки Du стратегия, которая призывает к отказу от сотрудничества, если другой игрок не сотрудничал, скажем, в пятнадцатом узле, определит тот же процесс (и поэтому те же самые платежи), что и Du. Компоненты, призывающие к сотрудничеству, в процессе никогда не задействуются, поскольку другой игрок не сотрудничает на пятнадцатом (или любом другом) ходу. Аналогичным образом стратегия, призывающая к сотрудничеству после факта второго сотрудничества, столь же успешна. Таким образом, эти и многие другие стратегии образуют с Du равновесие Нэша. Однако в некотором смысле все же можно сказать, что они не одинаково рациональны. Хотя они приводят к тем же самым платежам в узлах по пути, представляющему процесс игры, они не привели бы к тем же самым платежам, если бы были достигнуты другие узлы. Если первый игрок сотрудничал в прошлом, это для него отнюдь не повод сотрудничать теперь. Равновесие Нэша лишь требует, чтобы эти две стратегии наилучшим образом соответствовали друг другу по мере фактического развития игры. Более сильная концепция решения для игр развернутой формы требует, чтобы эти две стратегии продолжали быть наилучшими ответами друг другу независимо от того, какой узел на дереве игры был достигнут. Это понятие равновесия, совершенного по подыграм, выдвинул и отстаивал Рейнхард Зельтен (Selten 1975). Его можно выразить с помощью утверждения, что пара стратегий составляет равновесие Нэша для каждой подыгры первоначальной игры, где подыгра — результат принятия узла первоначальной игры за корень с полным отсечением всего, что от него не происходит.

В связи с новой, более сильной концепцией решения мы можем задать вопрос о решениях ИДЗ. Есть существенное теоретическое различие по этому вопросу между ИДЗ фиксированной конечной длины, схожих с изображенной выше, и ИДЗ с бесконечной или неопределенной конечной длиной. В играх первого вида можно доказать аргументом, известным как обратная индукция, что Du, Du является единственным равновесием, совершенным по подыграм. Предположим, игроки знают, что игра будет длиться точно n раундов. Тогда независимо от того, какой узел был достигнут, в раунде n−1 игроки сталкиваются перед обыкновенной («одноразовой») ДЗ и будут предавать. В раунде n−2 игроки знают, что независимо от их текущих действий в следующем раунде они оба откажутся от сотрудничества. Таким образом, для них рационально предать и теперь. Повторяя этот аргумент достаточное число раз, рациональные игроки делают вывод, что им следует отказываться от сотрудничества в каждом узле на дереве. Ведь отказ в каждом узле — наилучший ответ на любой ход, а иного равновесия, совершенного по подыграм, быть не может.

На практике нет большого различия между тем, как люди ведут себя в продолжительных ИДЗ фиксированной длины (кроме как в нескольких заключительных раундах) и ИДЗ неопределенной длины. А значит, часть допущений по поводу рациональности и общего знания, используемых в аргументе обратной индукции (и в других местах теории игр), нереалистична. Имеется обширный корпус текстов, авторы которых пытаются сформулировать аргумент тщательно, исследовать его допущения и пронаблюдать, как ослабление нереалистичных допущений могло бы изменить рационально приемлемые стратегии в ДЗ и других играх фиксированной длины. (Небольшую выборку см. в Bovens, Kreps et al., Kreps and Wilson, Pettit and Sugden 1989, Sobel 1993 и Binmore 1997.)

Предположим, первый игрок считает, будто имеется небольшой шанс, что второй станет придерживаться «иррациональной» стратегии, а не будет непрерывно предавать. Тогда рациональным для него будет часто сотрудничать самому. Действительно, даже если бы первый игрок был уверен в рациональности второго, сама его вера в возможность, что второй верит, будто он колеблется, могла бы иметь тот же эффект. А значит, аргумент в пользу непрерывного отказа в ИДЗ фиксированной длины зависит от сложных итеративных притязаний на определенное знание рациональности. Еще более нереалистичное допущение, отмеченное Рабиновичем и другими, звучит следующим образом: каждый игрок продолжает полагать, что другой совершит рациональный выбор на следующем ходу, даже после демонстрации им иррациональной игры на предыдущих ходах. Например, допускается, что в узле, достигнутом после длинного ряда ходов (C, C), …, (C, C), первый игрок выберет D, несмотря на то, что прежде так не поступал.

Некоторые исследователи, опираясь на подобного рода наблюдениях, утверждали, будто бы обратная индукция показывает, что стандартные допущения относительно рациональности (наряду с другими правдоподобными допущениями) являются непоследовательными или сами себя опровергают. Ведь, согласно правдоподобным допущениям, вести себя иррационально — один из способов гарантировать, что рациональный игрок засомневается в вашей рациональности. В ИДЗ фиксированной длины, например, первый игрок может быть в состоянии заключить, что если бы он должен был следовать соответствующей «иррациональной» стратегии, второй игрок реагировал бы рационально, так что в итоге они смогут достигнуть взаимного сотрудничества почти во всех раундах. Таким образом, из наших допущений следует и то, что первый игрок должен непрерывно отказываться от сотрудничества, и то, что он в большей мере преуспеет, если не будет так поступать. (См. Skyrms 1990: 125–139; Bicchieri 1989).

Многоножка и конечная ИДЗ

Многие из трудностей, связанных с ИДЗ фиксированной длины, могут возникнуть в еще более жесткой форме в рамках несколько более простой игры. Рассмотрим ДЗ, в которой платеж наказания равен нулю. Теперь повторим (итерационным путем) асинхронную версию этой игры фиксированное количество раз. Представим, что оба игрока могут следовать лишь «карательным» стратегиям, согласно которым они всегда должны предавать игрока, когда-либо отказывавшегося от сотрудничества. (Одна важная стратегия подобного рода разбирается ниже под обозначением GRIM.) На выходе мы имеем дело с игрой под названием многоножка. Особенно удачная реализация ее дана в Sobel 2005. На столе лежит пачка из n однодолларовых банкнот. Игроки поочередно берут из пачки по одной или две купюры за раз. Игра завершается, когда заканчивается пачка или один из игроков забирает две банкноты (независимо от того, какой исход наступил ранее). Оба игрока сохраняют на руках то, что успели взять. Развернутая форма игры для n=4 изображена ниже.

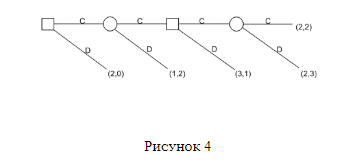
По-видимому, истинная многоножка (англ. centipede, букв. «стоножка») содержала бы 100 «ног», тогда как общую форму, разбираемую здесь, на деле следует называть «n-ножка». Игра обсуждалась впервые в Rosenthal 1981.

Как и в ДЗ фиксированной длины, обратная индукция с легкостью устанавливает, что рациональный игрок должен взять две купюры на первом ходу. Тем самым он получит платеж в 2 или 3 доллара в зависимости от того, ходит он первым или вторым, и оставит прочие n долларов из пачки нераспределенными. В более строгой терминологии единственное равновесие Нэша этой игры имеет место тогда, когда первый игрок берет два доллара на первом ходу, а единственное равновесие, совершенное по подыграм, — когда оба игрока берут по 2 доллара на любом подходе, который они должны совершить. Опять же, здравый смысл и данные экспериментов говорят о том, что в действительности игроки редко поступают таким образом. Это приводит нас к вопросу о том, какие именно допущения задействуются данным рассуждением и являются ли они реалистичными. (В дополнение к выборке, упомянутой в разделе о конечных итеративных ДЗ, см., напр., Aumann 1998, Selten 1978 и Rabinowicz 1998.) Многоножка также поднимает некоторые из тех же вопросов о сотрудничестве и желательном с точки зрения общества альтруизме, что ставит ДЗ, и является любимым инструментом в эмпирических исследованиях игрового процесса.

Бесконечная итерация

Рассмотрение бесконечно повторяющихся ДЗ помогает избежать сомнительного заключения обратной индукции, не погружаясь слишком глубоко в установление условий знания и рациональности. Разумеется, фактически люди не могут играть в бесконечно повторяющуюся игру, однако представляется, что бесконечные ИДЗ вполне способны смоделировать ряд взаимодействий, в рамках которых у участников никогда нет оснований полагать, что текущее их взаимодействие является последним. В такой ситуации пара стратегий определяет бесконечный путь через дерево игры. Если платежи одноразовой игры положительны, их сумма на любом таком пути бесконечна. А следовательно, сравнение стратегий оказывается затруднительным. Во многих случаях средний платеж за раунд достигает предела по мере увеличения числа раундов, так что сам этот предел уместно счесть платежом. (См. доводы в пользу этого тезиса в Binmore 1992: 365.) Например, если мы будем придерживаться лишь тех стратегий, что можно реализовать с помощью механических устройств (обладающих конечной памятью и скоростью вычислений), последовательность платежей каждому игроку после конечного числа раундов будет снова и снова циклически проходить через конкретную конечную последовательность платежей. Предел среднего платежа за раунд тогда будет средним платежом в цикле. В последние годы Пресс и Дайсон показали, что по многим причинам исследование бесконечной ИДЗ может быть ограничено «однопамятными» стратегиями, в которых вероятность сотрудничества в любом раунде зависит только от исхода предыдущей встречи стратегий. Их труд вдохновил много новых работ о бесконечной ИДЗ. (См. ниже Стратегии нулевого детерминанта.) Поскольку последний раунд отсутствует, очевидно, что обратная индукция не может применяться в бесконечной ИДЗ.

Неопределенная итерация

В большинстве современных исследований ИДЗ рассматриваются как имеющие не бесконечную и не фиксированную конечную, а неопределенную длину. Для этого достаточно включить в спецификацию игры такую вероятность p («тень будущего»), что в каждом раунде игра продолжится с вероятностью p. В другом варианте платежи после каждого раунда «дисконтируются» на коэффициент p так, чтобы соседние платежи были оценены более высоко, чем отдаленные. В математическом выражении различие невелико: расценивать p как вероятность продолжения или как дисконтирование платежей. Значение сотрудничества на каждой взятой стадии в ИДЗ явно зависит от вероятности встретить противников в более поздних раундах. (Было принято считать, что тем самым объясняется, почему уровень любезности выше в деревне, чем в столице, и почему клиенты склонны оставлять бо́льшие чаевые в местных ресторанах, чем в отдаленных). По мере того, как p приближается к нулю, ИДЗ становится одноразовой ДЗ, и количество отказов от сотрудничества увеличивается. По мере того, как p приближается к единице, ИДЗ становится бесконечной ИДЗ, и количество предательств уменьшается. Также принято утверждать, что игра обладает обозначенным выше свойством RCA, позволяющим (в симметричной игре) игрокам добиться большего успеха, сотрудничая в каждом раунде, чем если бы они «чередовали ходы» — вы сотрудничаете, в то время как я предаю, а затем я сотрудничаю, в то время как вы предаете.

В соответствии с одним из наблюдений (его источником, по-видимому, является Kavka 1983; более математическая форма дана в Carroll 1987) применение обратной индукции допустимо, пока верхняя граница длины игры является общим знанием. Ведь если такой верхней границей является b, тогда, добравшись до этапа b, игроки знают, что раунд является последним, а значит, им следует отказаться от сотрудничества. Если же они добрались до этапа b−1, они знают, что их поведение в этом раунде не сможет затронуть решение относительно предательства в следующем, и таким образом предадут. И т.д., и т.п. По всей видимости, не слишком трудно вычислить верхние границы по количеству взаимодействий в реальных ситуациях. Например, поскольку владелец магазина Джонс не может совершить больше одной продажи в секунду и будет жить менее тысячи лет, он и клиент Смит могут заключить (по самым осторожным подсчетам), что они сумеют совершить не более 1012 сделок. Полезно будет разобрать этот аргумент, чтобы утрировать допущения, сделанные в стандартных интерпретациях неопределенной ИДЗ и других неопределенно повторяющихся игр. Отметим вначале, что в описанной выше неопределенной ИДЗ не может существовать никакой верхней границы относительно длины игры. Вместо этого имеется некоторая фиксированная вероятность p, что в любой из моментов процесса игры она продолжит разыгрываться с вероятностью p. Если бы взаимодействие Смита и Джонса было смоделировано как неопределенная ИДЗ, то вероятность их взаимодействия через тысячу лет была бы не нулевой, а скорее некоторым числом больше pk, где p является вероятностью их взаимодействия в настоящий момент, а k — количеством секунд в тысяче лет. Более реалистичный способ смоделировать взаимодействие состоит в том, чтобы позволить значению p уменьшаться по мере развития игры. До тех пор, пока p стабильно остается больше нуля, верно, что верхняя граница количества возможных взаимодействий не существует, т.е. нет такого момента, в котором вероятность будущих взаимодействий стала бы равной нулю. Предположим, с другой стороны, будто бы наличествовала такая величина n, что при этом имелась нулевая вероятность продолжения игры до этапа n. Пусть p1, …,pn будут вероятностями, что игра продолжается после этапа 1, …, этапа n. Тогда должно быть наименьшее i, при котором pi становится равной 0. (Это случилось бы при i=n, если не раньше.) В рамках сделанных нами стандартных допущений касательно общего знания игроки знали бы это значение i, так что в итоге ИДЗ имела бы ту или иную фиксированную длину, а вовсе не являлась бы неопределенной ИДЗ. В случае владельца магазина и его клиента мы должны предположить, что оба знают сегодня, что их последнее взаимодействие произойдет, скажем, в полдень 10 июня 2020 года. Весьма правдоподобное соображение, с которого мы начали, а именно —некоторые верхние границы числа взаимодействий являются общим знанием, пускай и нет наименьшей верхней границы — несовместима с допущением, согласно которому мы с самого начала знаем все вероятности продолжения pi.

Как проницательно замечают Беккер и Кадд, мы не нуждаемся в верхней границе числа возможных итераций, чтобы сделать допустимой обратную индукцию в пользу отказа от сотрудничества. Если игроки изначально знают все значения pi, тогда до тех пор, пока значение pi остается достаточно малым, они (и мы) могут вычислить этап k, на котором риск будущего наказания и шанс на будущую награду более не перевешивают выгоду немедленного отказа от сотрудничества. Таким образом, они знают, что их противник будет предавать на этапе k, и начинается индукция. Эта модификация аргумента Кавки/Кэррола, однако, лишь более явно демонстрирует неправдоподобие своих допущений. Мало того, что Смит и Джонс якобы будут полагать, что есть ненулевая вероятность того, что они будут взаимодействовать через тысячу лет, каждый из них якобы будет в состоянии вычислить точный день, в который будущие взаимодействия станут и останутся настолько маловероятными, что их ожидаемый будущий доход перевешивается платежом того дня. Помимо этого каждый из них якобы будет полагать, что другой сделал это вычисление и что другой полагает, что он тоже его сделал, и т.д., и т.п.

Аксельрод

Итеративная версия ДЗ обсуждалась со времен изобретения игры, но интерес к ней значительно возрос после авторитетных публикаций Роберта Аксельрода в начале восьмидесятых. Аксельрод предложил профессиональным теоретикам игр прислать написанные ими компьютерные программы для игры в ИДЗ. Все они вошли в турнир, в рамках которого каждая программа играла со всеми остальными (а также со своим двойником и стратегией, которая сотрудничала и предавала наугад) сотни раз. Легко увидеть, что в подобной игре никакая стратегия не является «наилучшей» в том смысле, что ее счет оказался бы самым высоким по сравнению с любой группой конкурентов. Если бы другие стратегии никогда не рассматривали предыдущую историю взаимодействия при выборе своего следующего хода, был бы наилучшим безусловный отказ от сотрудничества. Если все другие стратегии начинают с сотрудничества и затем «наказывают» любое предательство, отказываясь от сотрудничества во всех последующих раундах, то более выгодна политика безусловного сотрудничества. Тем не менее, как и в прозрачной игре, некоторые стратегии обладают характеристиками, которые, по-видимому, позволяют им преуспевать в разнообразии сред. Стратегия, чей счет на исходном турнире Аксельрода оказался самым высоким, — «зуб за зуб» (далее ЗЗЗ) —предполагает просто сотрудничество в первом раунде и затем копирование предыдущего хода противника. Более существенным, чем изначальная победа ЗЗЗ, возможно, является то обстоятельство, что она выиграла второй турнир Аксельрода, шестьдесят три участника которого все пришли к результатам первого турнира. Анализируя второй турнир, Аксельрод отметил, что каждому из участников можно было бы приписать одну из пяти «представительных» стратегий таким образом, что успех стратегии по сравнению с рядом других оказался бы точно предсказан ее победой над их представителем. В качестве дальнейшей демонстрации силы ЗЗЗ Аксельрод вычислил счет, который каждая стратегия получит на турнирах, где одна из представительных стратегий будет в пять раз более распространена, чем на оригинальном турнире. ЗЗЗ победила с самым высоким счетом во всех гипотетических турнирах, кроме одного.

По мнению Аксельрода, своим успехом ЗЗЗ была обязана четырем свойствам. Она благосклонна, т.е. никогда не призывает первым делом к отказу от сотрудничества. Восемь благосклонных участников на турнире Аксельрода были восемью наиболее преуспевающими стратегиями. Она является ответной, что делает трудным ее использование по неблагосклонным правилам. Она незлопамятна, т.е. проявляет желание сотрудничать даже с теми, кто прежде отказывался от сотрудничества (если предательство не было совершено ими непосредственно в предшествующем раунде). Злопамятное правило в принципе неспособно привести к получению платежа награды после того, как противник однажды предал. И она ясна, т.е. другим стратегиям легче предсказывать ее поведение с тем, чтобы суметь наладить взаимовыгодное взаимодействие.

Аргументация Аксельрода весьма привлекательна. Стоит отметить, тем не менее, что его идеи сформулированы недостаточно точно, чтобы они могли служить строгим доказательством превосходства ЗЗЗ. Никто не знает, например, объем класса стратегий, которые могли бы обладать указанными четырьмя свойствами, или критерии успеха, подразумеваемые при их наличии. Верно, что если противник играет ЗЗЗ (и тень будущего является достаточно большой), тогда максимальный платеж приобретается в соответствии со стратегией, приводящей к взаимному сотрудничеству в каждом раунде. Поскольку ЗЗЗ сама является одной из таких стратегий, отсюда следует, что ЗЗЗ образует равновесие Нэша с собой в пространстве всех стратегий. Однако это не слишком выделяет ЗЗЗ, ведь Du, Du также является равновесием Нэша. Действительно, из «народной теоремы» итеративной теории игр (теперь широко упоминаемой — см., напр., Binmore 1992: 373–377) следует, что для любого p (0≤p≤1) имеется равновесие Нэша, в котором p является интервалом времени, когда возникает взаимное сотрудничество. Действительно, ЗЗЗ в некотором отношении хуже, чем многие другие равновесные стратегии, поскольку народная теорема может быть заострена к схожему результату в отношении равновесия, совершенного по подыграм. ЗЗЗ в общем случае не является совершенной по подыграм. Ведь если один игрок в ЗЗЗ (вопреки ожиданиям) откажется от сотрудничества с другим в единственном раунде, второй добьется большего успеха, сотрудничая безусловно.

Итерация с ошибкой

В обзоре исследовательского поля через несколько лет после обнародования изложенных выше результатов Аксельрод и Дайон отметили несколько успехов ЗЗЗ и ее модификаций. Они заключили, что «исследование показало, что многие из полученных Аксельродом данных… могут быть обобщены до обстоятельств, которые в значительной степени отличаются от исходной итерационной ДЗ с двумя игроками». Однако при некоторых умеренных обстоятельствах ЗЗЗ имеет серьезные недостатки. В одном из таких случаев, отмеченном Аксельродом и Дайоном, речь идет о попытках правдоподобно допустить, что игроки подвержены ошибкам исполнения и восприятия. Такое допущение можно сделать множеством способов. Бендор, например, говорит в этой связи о «шумных платежах». Когда игрок сотрудничает, в то время как его противник отказывается от сотрудничества, его платеж равен S+e, где e является случайной величиной, ожидаемая стоимость которой — 0. Каждый игрок выводит ход других из собственного платежа, так что если e является достаточно высоким, вывод может оказаться ошибочным. Сагден, в свою очередь, рассматривает игроков, которые имеют определенную вероятность совершения ошибки исполнения, которая очевидна для них, но не для их противников (Sugden 1986: 112–115). Такие игроки могут преследовать стратегии, в соответствии с которыми они «заглаживают» ошибочные предательства, будучи в поздних раундах более кооперативными, чем они были бы после намеренного предательства. Если допустить, что сами игроки не могут отличить ошибочный ход или наблюдение от подлинного, самый простой способ смоделировать неизбежность ошибки состоит в полном запрете детерминистических стратегий типа ЗЗЗ и замене их на «несовершенные» аналоги наподобие «копируй последний ход другого игрока с вероятностью 99% и совершай обратный ход с вероятностью 1%». Несовершенная ЗЗЗ является намного менее притягательной, чем ее детерминистский родственник, поскольку когда две несовершенные стратегии ЗЗЗ играют друг против друга, «ошибка» любой из них выделит длинную цепочку ходов, в которых игроки будут поочередно отказываться от сотрудничества. В длинной итерационной игре между двумя несовершенными ЗЗЗ с любой вероятностью ошибки p, где 0<p<, игроки приблизятся к тем же средним платежам, что и в игре, разворачивающейся между двумя стратегиями, которые выбирают беспорядочно между сотрудничеством и предательством, а именно (R+P+S+T). Это значительно хуже, чем платеж R, который игрок получает, когда p=0.

Преобладающее мнение состоит в том, что когда речь идет о неизбежном несовершенстве, успешные стратегии должны будут в большей степени прощать предательства своим противникам (так как эти предательства могли быть непреднамеренными). Как показывает Моландер (Molander 1985), стратегии, сочетающие ЗЗЗ с Cu, действительно приближаются к платежу R, поскольку вероятность ошибки стремится к нулю. Когда такие смеси играют друг против друга, они извлекают выгоду из более высоких соотношений Cu к ЗЗЗ, но если они становятся слишком «щедрыми», они рискуют подвергнуться эксплуатации «скаредными» стратегиями, смешивающими ЗЗЗ с отказом от сотрудничества. Моландер вычислил, что когда смесь установлена таким образом, чтобы после предательства каждый сотрудничал с вероятностью g(R,P,T,S)=min{1−(T−R)/(R−S),(R−P)/(T−P)}, щедрые стратегии получат самый высокий из всех возможных счет в игре друг с другом, не позволяя скаредным стратегиям добиться против них большего успеха, чем ЗЗЗ. Следуя Новаку и Зигмунду, мы называем эту стратегию щедрая ЗЗЗ, или ЩЗЗЗ. Когда платежи имеют общие оценки 5,3,1,0 (как в Axelrod 1984), ЩЗЗЗ сотрудничает после каждого случая сотрудничества противника и после 25% предательств противника.

Идея, что наличие несовершенства стимулирует большее великодушие или большую щедрость, правдоподобна только в отношении низких уровней несовершенства. Как только уровень достигает , несовершенная ЗЗЗ становится неотличимой от случайной стратегии, для которой весьма невеликодушная Du является лучшим ответом. Симуляция Коллока, по всей видимости, подтверждает, что при высоких уровнях несовершенства большая скаредность является лучшей политикой, чем большее великодушие. Но Бендор, Крамер и Свистак отмечают, что стратегии, используемые в симуляции Коллока, не являются представительными, а стало быть, результаты должны интерпретироваться с осторожностью.

Вторая идея состоит в том, что несовершенная среда поощряет стратегии наблюдать за игрой их противника более тщательно. На турнире, подобном турниру Аксельрода (Donninger 1986), в котором ходы каждого игрока были подчинены десятипроцентному шансу на изменение, ЗЗЗ финишировала шестой из двадцати одной стратегии. Сторонники преобладающего представления могли бы заявить, что ее предсказуемо побила более щедрая ЗЗЗ: «зуб за два зуба» (которая сотрудничает, если не предавала два раза подряд). Она также была побита, однако, двумя версиями Downing, программы, которая основывает каждый свой новый ход на своей наилучшей оценке того, насколько внимательным ее противник был к его предшествующим ходам. На двух исходных турнирах Аксельрода программа Downing заняла третье место в нижней части списка представленных программ. Бендор в ряде выводов показывает, что в ходе борьбы против несовершенных стратегий более выгодно основывать оценку вероятности предательства на более длинных историях, чем это делает ЗЗЗ (Bendor 1987).

Идея, согласно которой стратегии в несовершенной среде должны обращать внимание на свои предшествующие взаимодействия, была эффективно воплощена в семействе «павловских» стратегий (исследованных в Kraines and Kraines 1989, 1993). Для каждого натурального числа n верно, что n-Pavlov, или Pn, регулирует его вероятность сотрудничества в единицах в соответствии с тем, насколько успешно все проходило в предыдущем раунде. Более точно, если Pn сотрудничал с вероятностью p в последнем раунде, то в этом раунде он будет сотрудничать с вероятностью p[+], если получил платеж награды на предыдущем раунде, p[−], если получил платеж наказания, p[+], если получил платеж искушения, и p[−], если получил платеж простака. Знаки [+] и [−] обозначают ограниченное сложение и вычитание, т.е. x[+]y является суммой x+y, если это количество не превышает единицу, в противном случае оно равняется единице (или приближается к ней в той мере, насколько возможность ошибки это допускает), а x[−]y аналогичным образом либо равно x−y, либо близко к нулю. Строго говоря, Pn не определен полностью, пока начальная вероятность сотрудничества не задана, но для большинства целей значение этого параметра становится незначительным в достаточно длинных играх и может благополучно игнорироваться. Может выйти так, что Pn потребует гораздо больше вычислительных ресурсов, чем, скажем, ЗЗЗ. Каждый ход последней зависит только от завершающего хода ее противника, тогда как каждый ход Pn — это функция от всей истории предыдущих ходов обоих игроков. Pn, однако, всегда может вычислить свой следующий ход, следя только за текущей вероятностью сотрудничества и последним платежом. Как говорят его авторы, все это напоминает «естественную стратегию в мире животных». Можно вычислить, что при n>1 Pn добивается большего успеха против случайной стратегии, чем это делает ЗЗЗ. Если говорить более широко, Pn достигает того же или большего успеха, чем ЗЗЗ, в борьбе против щедрых безответных стратегий Cp, которые всегда сотрудничают с фиксированной вероятностью p≥ (поскольку случайный платеж искушения может научить его эксплуатировать безответные стратегии). В этих случаях «медленно обучающиеся» версии Павлова с более высокими значениями n добьются несколько лучшего результата, чем «быстро обучающиеся» версии с низкими значениями. В схватке против ответных стратегий, подобных прочим стратегиям Павлова и ЗЗЗ, Pn и его противник в конечном счете достигают состояния (почти) постоянного сотрудничества. Итоговый платеж тогда будет обратно пропорционален «периоду обучения», т.е. количеству раундов, необходимых для достижения этого состояния. Поскольку период обучения Pn экспоненциально зависит от n, Крэйнсы утверждают, что P3 или P4 должны быть предпочитаться другим павловским стратегиям, поскольку они близки к «идеальным» стратегиям ИДЗ. Следует отметить, однако, что когда (детерминистская) ЗЗЗ играет против себя, никакой период обучения не требуется вообще, тогда как когда павловская стратегия играет против ЗЗЗ или другого Павлова, такой период может оказаться очень долгим. Таким образом, убедительность аргумента в пользу превосходства стратегии Павлова над ЗЗЗ определяется наблюдением, согласно которому ее исполнение меньше деградирует под воздействием несовершенств. Следует также помнить, что ни одна стратегия не является наилучшей в любой среде и что критерии, на которые ссылаются при защите различных стратегий в ИДЗ, являются смутными и неоднородными. Одно из преимуществ эволюционных версий ИДЗ, разбираемых в следующем разделе, состоит в том, что они допускают более осторожную формулировку и оценку критериев успеха.

Эволюция

По всей вероятности, эволюционные версии ДЗ — самая активная область исследования игры. Популяция игроков, использующих различные стратегии, играет в ИДЗ между собой. Число стратегий с более низким счетом убывает, а число стратегий с более высоким растет, и процесс все время повторяется. Таким образом, чтобы достигнуть успеха в эволюционной ДЗ (далее ЭДЗ), нужно преуспеть в борьбе с другими успешными стратегиями, а не просто достигать большего успеха по сравнению с широким диапазоном стратегий. Начальная популяция в ЭДЗ может быть представлена рядом пар {(p1,s1), … (pn,sn)}, где p1…pn являются пропорциональми долями популяции, играющими стратегии s1, …,sn соответственно. Описание ЭДЗ, данное выше, не определяет, как именно популяция стратегий будет воссоздаваться после каждой ИДЗ. Согласно обычному допущению (и самому адекватному для биологических применений), результат в любом раунде указывает на относительное число «потомства» в следующем. Предполагается, что размер всей популяции остается неизменным, так что рождения более успешных стратегий в точности возмещаются смертностью менее успешных. Иными словами, соотношение p*i из каждой стратегии si в последующей популяции определяется уравнением p*i=pi(Vi/V), где Vi является результатом si в предыдущем раунде, а V является средним числом всех очков в популяции. Таким образом, количество стратегий, чей счет превосходит среднее число очков по популяции, увеличится, а число стратегий со счетом, уступающим среднему, уменьшится. Этот вид эволюции называется «репликаторной динамикой», или эволюцией согласно правилу «пропорциональной приспособленности». Возможны и другие правила эволюции. Как утверждают Бендор и Свистак утверждают, в отношении социальных применений полезнее считать, что игроки переключаются с одной стратегии на другую, а не появляются и исчезают. Поскольку рациональные игроки предположительно переключились бы только на стратегии, которые получили самый высокий платеж в предыдущих раундах, численно возрастут лишь стратегии с наиболее высоким счетом. Батали и Китчер задействуют динамику, в рамках которой стратегии с низшим счетом заменяются стратегиями, которые смешивают характеристики стратегий с высшим счетом. Множество других возможных разновидностей эволюционной динамики описано и сопоставлено в Kuhn 2004. Настоящий разбор, однако, будет касаться прежде всего ЭДЗ с правилом пропорциональной приспособленности.

Публикации Аксельрода, следующего в данной связи по стопам Триверса и Мэйнарда Смита, включают описание ЭДЗ с пропорциональной приспособленностью и краткий анализ эволюционной версии его турнира ИДЗ. Для Аксельрода ЭДЗ предоставляет еще одно свидетельство в пользу ЗЗЗ:

Стратегия «Зуб за зуб» имела очень незначительное преимущество в первоначальном турнире и ни разу не утрачивала его в симулированных поколениях. К тысячному поколению она стала самым успешным правилом и по-прежнему росла с более высокой скоростью, чем любое другое правило.

Турнир ЭДЗ Аксельрода, однако, обладал рядом свойств, которые можно было бы посчитать искусственными. Во-первых, он допускал детерминистские стратегии в среде без шума. Как было отмечено выше, можно ожидать, что ЗЗЗ меньше преуспеет при условиях, которые моделируют неизбежность ошибки. Во-вторых, турнир стартовал лишь с 63 стратегиями из исходного турнира ИДЗ. Успех в борьбе против стратегий, созданных в башне из слоновой кости, возможно, не подразумевает превосходство над всеми теми стратегиями, которые могли бы быть найдены в природе. В-третьих, конкурировать на данном этапе было разрешено лишь стратегиям, выжившим на предыдущем этапе. Можно возразить, что более реалистичная модель позволила бы новым стратегиям-«мутантам» войти в игру на любом этапе. Изменение этого третьего параметра вполне могло бы нанести ущерб ЗЗЗ. Для большого роста в ЗЗЗ популяция позволила бы мутантам, использующим более наивные стратегии типа Cu, восстанавливаться на исходной позиции, а присутствие наивных игроков в популяции могло бы одобрить более опасные стратегии, подобные Du над ЗЗЗ.

Новак и Зигмунд создали симуляции двух разновидностей турниров, которые избегают трех сомнительных свойств. Первая симуляция исследовала семейство «реактивных» стратегий. Для любых вероятностей y, p, и q верно, что R(y,p,q) является стратегией сотрудничества с вероятностью y в первом раунде и далее с вероятностью p, если другой игрок сотрудничал в предыдущем раунде, или с вероятностью q, если он отказался от сотрудничества. Это широкое семейство, включающее многие из ранее рассмотренных стратегий. Cu, Du, ЗЗЗ и Cp являются R(1,1,1), R(0,0,0), R(1,1,0) и R(p,p,p). ЩЗЗЗ, когда платежи составляют 5,3,1,0, является R(1,1,.25). Чтобы отразить в том числе и неизбежность ошибки, Новак и Зигмунд исключают из турниров детерминистские стратегии, в которых p и q равны 1 или 0. Как и прежде, если игра достаточно длинна (и p и q не целые числа), первый ход может игнорироваться, и может быть идентифицирована реактивная стратегия со значениями p и q. Особое внимание уделяется стратегиям, близким к ЩЗЗЗ Моландера, описанной выше, в которой p=1 и q=min{1−(T−R)/(R−S),(R−P)/(T−P)}. Первые серии турниров ЭДЗ Новака и Зигмунда начинаются с представительных выборок реактивных стратегий. В отношении большинства турниров они обнаружили, что эволюция вела безвозвратно к Du. Стратегии R(p,q), самые близкие к R(0,0), процветали, тогда как остальные погибали. Тем не менее, когда одна из начальных стратегий очень близка к ЗЗЗ, исход меняется.

Кажется, что ЗЗЗ и все другие реципрокные стратегии (вблизи (1,0)) исчезают. Но выдерживающее натиск меньшинство остается и сопротивляется. Перелом наступает, когда «простаки» столь истощены, что эксплуататоры уже не могут ими питаться. Сначала медленно, но постепенно набирая обороты, возвращаются реципрокные игроки, и эксплуататоры приходят в упадок. Однако схожая с ЗЗЗ стратегия, вызвавшая поворот фортуны, не собирается получать из него выгоду: как только эксплуататоры устранены, ее задача выполнена, и на смену ей идет стратегия, наиболее близкая к ЩЗЗЗ. Эволюция после этого останавливается. Даже если мы иногда привносим 1% другой стратегии, она растворяется.

На основе проведенных ими турниров Новак и Зигмунд выдвинули гипотезу, что ЗЗЗ играет важнейшую роль в появлении сотрудничества, однако именно ЩЗЗЗ, скорее, оказывается стратегией, которая на деле обуславливает устойчивые паттерны сотрудничества в биологическом мире.

Вторая серия симуляций с более широким классом стратегий, тем не менее, вынудила их изменить свое мнение. Стратегии, рассмотренные во второй серии, позволили каждому игроку основывать вероятность сотрудничества как на его собственном предыдущем ходу, так и на ходу противника. Стратегия может теперь быть представлена как S(p1,p2.p3,p4), где p1,p2,p3,p4 являются вероятностями сотрудничества после исходов (C,C), (C,D), (D,C) и (D,D) соответственно, т.е. после получения платежей награды, простака, искушения и наказания. (Опять же, мы можем игнорировать вероятность предательства на первом ходу, пока pi не равны нулю или единице.) Начальная популяция на этих турнирах играет против случайной стратегии S(.5,.5,.5,.5), и после каждой сотни поколений вводится небольшое число особей случайно (недетерминистски) выбранного мутанта, и популяция развивается согласно пропорциональной приспособленности. Результаты существенно отличаются от предыдущих. После 107 поколений состояние устойчивого взаимного сотрудничества было достигнуто в 90% запусков симуляции. Но менее чем 8,3 % этих состояний были заселены игроками, использующими ЗЗЗ или ЩЗЗЗ. Оставшиеся 91,7 % доминировались стратегиями, близкими к S(1,0,0,1). Такова лишь павловская стратегия P1 Крэйнсов, которая переигрывает свой последний ход после получения R или T и изменяется к другому ходу после получения P или S. Крэйнсы относились к P1 несколько пренебрежительно. Они вспоминают, что Рапопорт и Чамма, встретившие ее на раннем этапе истории теории игр, обозначили ее словом «простофиля» и заметили, что «название полностью заслужено». Действительно, P1 имеет печальную склонность сотрудничать с Du на каждом следующем витке и в борьбе против ЗЗЗ может оказаться заблокированной в низшей серии повторения платежей T,P,S,T,P,S, …. Но Новак и Зигмунд переименовывают стратегию — теперь она называется «кнут и пряник» — и возвещают ее преимущества. Их симуляции предполагают, что упомянутые здесь отказы от сотрудничества не были столь значимы в эволюционных контекстах. Одна из причин заключается в том, что P1 помогает делать среду неподходящей для его врагов. Du преуспевает в среде с щедрыми стратегиями типа Cu или ЩЗЗЗ. ЗЗЗ, как мы уже видели, позволяет этим стратегиям процветать, что может проложить путь к Du. Таким образом, хотя ЗЗЗ преуспевает в соревновании с Du не так плохо, как P1, P1 больше преуспевает в сохранении среды от Du.

Симуляции во вселенной детерминистских стратегий приводят к результатам, весьма отличным от данных Новака и Зигмунда. Брюс Линстер (Linster 1992, 1994) предполагает, что естественные классы стратегий и реалистичные механизмы эволюции могут быть определены представлением стратегий как простых автоматов Мура. Например, P1 представлена автоматом, изображенным ниже.

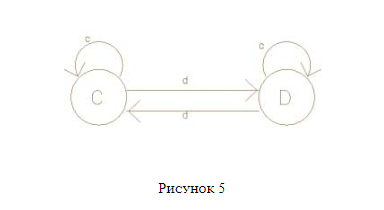
Этот автомат имеет два состояния, обозначенные кругами. Все начинается в крайнем левом состоянии. C в левом круге означает, что автомат сотрудничает на первом ходу. Стрелка, ведущая слева к правому кругу, указывает, что автомат отказывается от сотрудничества (переходит в D) после того, как оно имело место (в состоянии C), и его противник также отказался (стрелка обозначена d). Линстер провел симуляции эволюционной ДЗ среди стратегий, которые могут быть представлены автоматами Мура с двумя состояниями. Оказывается, что они в точности являются детерминистскими версиями стратегий S Новака и Зигмунда. Поскольку стратегии являются детерминистскими, мы должны различать версии, которые сотрудничают в первом раунде, и те, что отказываются от сотрудничества в первом раунде. Среди сотрудничающих в первом раунде S(1,1,1,1), S(1,1,1,0), S(1,1,0,1) и S(1,1,0,0) все представляют стратегию Cu безусловного сотрудничества. Точно так же все четверо отказывающихся представляют Du. Каждый из других S(p1,p2,p3,p4), где p1,p2,p3,p4 являются или нулем, или единицей, представляет уникальную стратегию, и каждый образует две разновидности сообразно тому, сотрудничает он или предает в первом раунде. Удаляя шесть дубликатов из этих 32 детерминистских версий стратегий Новака и Зигмунда, мы получаем 26 стратегий «с двумя состояниями», которые рассматривает Линстер.

Линстер симулировал множество турниров ЭДЗ среди стратегий с двумя состояниями. Некоторые используют «равномерную мутацию», в которой каждая стратегия в популяции имеет равную вероятность m мутирования в любую из других стратегий. Некоторые используют «стилизованную мутацию», в которой единственными разрешенными мутациями являются те, которые могут быть поняты как результат единственной «нарушенной связи» в диаграммах автомата Мура. В некоторых симуляциях мутации происходят у крошечной доли популяции в каждом поколении; в других «мутанты» представляют силу вторжения, составляющую один процент первоначальной популяции. В некоторых турнирах было наложено наказание за увеличившуюся сложность в виде сокращенных платежей для автоматов, требующих большего количества состояний или связей. Как можно было ожидать, в зависимости от условий результаты изменяются. Однако обнаруживаются поразительные различия между всеми результатами Линстера и данными Новака и Зигмунда. На турнирах Линстера ни одна стратегия не доминировала когда-либо выживающие популяции так, как это делали P1 и ЩЗЗЗ у Новака и Зигмунда. Одна стратегия, которая все же сумела охватить более пятидесяти процентов популяции, была изначально-сотрудничающей версией S(1,0,0,0). Это стратегия, несовершенные варианты которой, по всей видимости, являлись весьма неконкурентоспособными для Новака и Зигмунда. Она часто обсуждалась в литературе по теории игр под обозначением GRIM (суровый) или TRIGGER (спусковой механизм). Она сотрудничает, пока противник однажды не предал, и затем предает всю оставшуюся часть игры. Согласно Скирмсу (Skyrms 1998) и Вандерскрафу, Гоббс и Юм рассматривали ее как стратегию, которая лежит в основе нашего кооперативного поведения в важных ситуациях, сходных с ДЗ. Объяснение несоответствия между высокой результативностью GRIM для Линстера и ее низкой результативностью для Новака и Зигмунда, вероятно, так или иначе относится к ее резкому ухудшению при наличии ошибки. В матче с двумя несовершенными GRIM «ошибочный» отказ от сотрудничества любого приводит к длинной череде взаимных отказов. Таким образом, в конечном счете несовершенная GRIM проигрывает самой себе. Другие стратегии, которые пережили (в меньших количествах) турниры Линстера: ЗЗЗ, P1, Cu и изначально-кооперативная S(1,0,1,1). (Заметьте, что несовершенная GRIM также, по всей вероятности, выступит плохо против их несовершенных версий.) Наблюдение, в соответствии с которым эволюция могла бы привести к устойчивой смеси стратегий (вероятно, каждая бы старалась защитить других от захватчиков конкретного типа), а не к единственной доминирующей стратегии, довольно соблазнительно. Столь же соблазнителен результат, полученный при нескольких особых условиях, в которых эволюция приводит к повторению цикла популяционных смесей.

Ожидается, что станет возможно определять стратегии, которые будут преобладать в ЭДЗ с различными условиями, и подкреплять такие предсказания формальными доказательствами. До недавнего времени, однако, математические анализы ЭДЗ страдали от концептуальных неурядиц относительно условия «эволюционной устойчивости», при котором, как говорят Новак и Зигмунд, «эволюция останавливается». В Axelrod 1984 и Axelrod and Hamilton 1981 утверждается, что ЗЗЗ является эволюционно устойчивой. Selten 1983 включает пример игры без эволюционно устойчивой стратегии. Доводы Селтена, согласно которым такой стратегии не существует, явно адресован ЭДЗ и другим эволюционным играм. В Boyd and Lorberbaum 1987, а также в Farrell and Ware 1989 предоставляются другие доказательства, из которых следует, что никакие стратегии для ЭДЗ не являются эволюционно устойчивыми. Как и следовало ожидать, парадокс разрешается очень просто: все три группы авторов применяют отличающиеся друг от друга концепции эволюционной устойчивости. Концептуальная путаница устраняется в ряде статей Бендора и Свистака. Два основных понятия устойчивости описываются и применяются к ЭДЗ ниже. Читатели, которые пожелают сравнить их с некоторыми другими, фигурирующими в литературе, могут обратиться к следующему краткому справочнику:

Концепции устойчивости в эволюционных играх.

Стратегия s для эволюционной игры имеет универсальную сильную узкую устойчивость («USN-устойчивость»), если преследование стратегии s популяцией приводит по любому правилу эволюции к вымиранию любой достаточно малой группы захватчиков, все из которых придерживаются той же стратегии. Эволюционная игра имеет USN-устойчивость лишь в том случае, если отвечает простому условию платежей, установленному Мэйнардом Смитом (MS):

— (MS) Для всех стратегий j верно, что V(i,i)>V(j,i), или же верно, что V(i,i)=V(j,i) и V(i,j)>V(j,j).

(Здесь и далее V(i,j) обозначает платеж стратегии i, когда i играет j.) Согласно MS, любые захватчики добиваются строго меньшего успеха в борьбе против местных, чем сами местные в борьбе против местных. В ином случае они получают точно тот же платеж в схватке с местными, что и сами местные, но местный добивается большего успеха в схватке с захватчиком, нежели сам захватчик.

Для любой стратегии i в ИДЗ (или даже во всякой итерационной конечной игре), однако, имеются отличные от i стратегии j, которые подражают ходам i, когда те играют против i или j. Существование этих «нейтральных мутантов» подразумевает, что MS не может быть удовлетворено, а следовательно, ни одна из ЭДЗ не имеет USN-устойчивости. Этот аргумент, конечно, опирается на допущение, в соответствии с которым любая стратегия в итерационной игре является возможным захватчиком. Вполне может иметься основание для ограничения числа доступных стратегий. Например, если предполагается, что игроки не имеют знания о предыдущих взаимодействиях, приемлемо ограничить область доступных стратегий до безусловных. Поскольку пара игроков тогда получает одни и те же платежи в каждом раунде итеративной игры, было бы уместно также рассматривать каждый раунд эволюционной игры в качестве одноразовой игры между каждой парой игроков, а не как итерационную игру. В самом деле, именно подобного рода эволюционную игру и рассматривал сам Мэйнард Смит. В рамках обозначенного подхода требованию MS удовлетворяет любая стратегия S, в которой (S,S) является строгим равновесием Нэша в соответствующей одноразовой игре (включая безусловный отказ от сотрудничества в ДЗ). Выходит, что MS и USN-устойчивость в некоторых контекстах являются нетривиальными условиями.

Стратегия s имеет ограниченную слабую широкую устойчивость (или RWB-устойчивость), если в том случае, когда эволюция протекает согласно правилу пропорциональной приспособленности и местная популяция играет s, любая (возможно, неоднородная) группа захватчиков достаточно малого размера будет не в состоянии привести местных к вымиранию. Это условие оказывается эквивалентным ослабленной версии MS, сформулированной Бендором и Свистаком (BS).

—(BS) Для всех стратегий j верно, что V(i,i)>V(j,i), или же верно, что V(i,i)=V(j,i) и V(i,j)≥V(j,j).

BS и RWB-устойчивость — нетривиальные условия в более общем эволюционном подходе: стратегии для ЭДЗ, обладающие RWB-устойчивостью, действительно существуют. Однако само это обстоятельство, собственно, не оправдывает ни одну из разобранных выше стратегий. Выводы Бендора и Свистака аналогичны ранее упомянутой народной теореме. Если тень будущего достаточно велика, то существуют RWB-устойчивые стратегии, поддерживающие любую степень сотрудничества от нуля до единицы. Один из способов различить стратегии, которые отвечают BS, состоит в определении размера вторжения, необходимого для того, чтобы повергнуть местных, или (что то же самое) доли местных, требуемой для поддержания устойчивости. Как показывают Бендор и Свистак, это число, т.е. минимальная частота стабилизации, никогда не превышает 1/2: никакая популяция не может сопротивляться любой группе вторжения того же размера, что и она сама. Они утверждают, что этот результат действительно позволяет им предоставить теоретическое обоснование заявлений Аксельрода. Бендор и Свистак демонстрируют, что по мере того как ее достигает тень будущего, любая хорошая (т.е. та, что никогда не предаст первой) и ответная (т.е. та, что всегда незамедлительно предает после того, как предали ее) стратегии имеют минимальную частоту стабилизации, приближающуюся к одной второй. ЗЗЗ обладает обоими указанными свойствами. Фактически они представляют собой первые два из четырех свойств, которые Аксельрод полагал определяющими в успехе ЗЗЗ. Разумеется, есть много других хороших и ответных стратегий, а также имеются стратегии (наподобие P1), которые не являются ответными, но все же удовлетворяют RWB-устойчивости. Но Бендор и Свистак по меньшей мере показывают, что любая «максимально прочная» (минимальная частота стабилизации которой приближается к одной второй) стратегия выбирает сотрудничество во всех ходах, кроме ограниченного их числа, в бесконечно повторяющейся ДЗ.

Выводы Бендора и Свистака должны интерпретироваться с некоторой осторожностью. Во-первых, нужно иметь в виду, что никакие вероятностные или чувствительные к шуму стратегии не могут соответствовать определениям «хорошая» или «ответная». Более того, несовершенные версии ЗЗЗ не удовлетворяют RWB-устойчивости. Они могут быть свергнуты достаточно малыми вторжениями детерминистической ЗЗЗ или даже произвольными небольшими вторжениями любой менее несовершенной ЗЗЗ. Во-вторых, следует помнить, что выводы касательно минимальных частот стабилизации касаются только слабой устойчивости. Если число поколений является большим по сравнению с исходной популяцией (как это зачастую случается в биологических применениях), популяция, которая изначально целиком состояла из игроков, использующих одну и ту же максимально прочную стратегию, вполне может допустить последовательность небольших групп вторжения, которая в конечном счете сокращает объем исходной стратегии до менее чем половины популяции. На данном этапе исходная стратегия может потерпеть крах.

Вероятно, оба эти предостережения играют роль в объяснении очевидного несоответствия между результатами Бендора–Свистака и симуляциями Новака–Зигмунда. Можно было бы ожидать, что минимальная частота стабилизации Бендора–Свистака предоставит указание на период времени, в который популяция играет специфическую стратегию. Стратегия, требующая большого вторжения для свержения, вероятно, будет преобладать дольше, нежели стратегия, требующая лишь небольшого вторжения. Прямой расчет показывает, что P1 имеет относительно низкую минимальную частоту стабилизации. Эта стратегия свергается вторжениями безусловных предателей, превышающими 10% популяции. И все же в симуляциях Новака–Зигмунда стратегии, подобные P1, преобладают над стратегиями, подобными ЗЗЗ. Поскольку симуляции требовали несовершенства и поскольку они породили последовательность мутантов, значительно превышающую исходную популяцию, о действительном противоречии здесь не идет и речи. Однако несоответствие предполагает, что мы еще не обладаем теоретическим пониманием ЭДЗ, достаточным для предсказаний касательно стратегий, которые появятся при различных правдоподобных условиях.

Как и в случае с USN-устойчивостью, понятие RWB-устойчивости может быть более дифференцирующим, если будет соотнесено со специфическим множеством стратегий. Исследование Molander 1992 версии ДЗ со многими участниками Шеллинга, например, ограничивает внимание семейством {S1, …,Sn} стратегий, подобных ЗЗЗ. Игрок, придерживающийся Si, сотрудничает в первом раунде и в каждом последующем раунде после того, как по меньшей мере i других сотрудничают. Рассматривая устойчивость как сопротивление вторжениям других членов семейства, Моландер оказывается в состоянии показать, что существуют такие условия, при которых некоторая смесь двух Si (одна из которых эквивалентна Du) является уникально устойчивой. Значение подобных выводов, тем не менее, зависит от правдоподобия таких ограничений на множестве допустимых стратегий.

Эволюция и опциональная ДЗ

В итерационных и эволюционных версиях опциональных ДЗ мы представляем, что игроки из некоторой популяции неоднократно разделяются на пары и получают возможность сыграть в ДЗ (выбирая C либо D) или выйти из игры (выбор N). Выбирая N, игрок воздерживается от возможности получения награды или платежей искушения до следующего соединения в пару. В большинстве человеческих взаимодействий, которые приходят на ум, отказ взаимодействовать с определенным партнером отнюдь не представляет ту же самую потерю возможности взаимодействовать с другим, которая имеется у принятия участия. Если я покупаю автомобиль у недобросовестного продавца, я должен буду прождать долгое время, прежде чем моя следующая закупка достигнет большего успеха; однако если я отказываюсь взаимодействовать, я могу незамедлительно начать вести переговоры с соседним продавцом. Тем не менее, при взаимодействии людей (а также, что более вероятно, нечеловеческих животных либо наций или корпораций) возникают ситуации, которые вполне могут быть смоделированы эволюционными версиями опциональной ДЗ.

Мы можем обозначить стратегии для эволюционной опциональной ДЗ, которые не требуют памяти о предыдущем взаимодействии, тройками <p,q,r>, где p, q и r являются вещественными числами, прибавляющимися к единице, представляя вероятность сыграть C, D и N. Ни одна из таких стратегий не отвечает условию BS, а следовательно, не является RWB-устойчивой в пределах этого семейства. Если все члены группы безоговорочно отказываются участвовать (придерживаясь <0,0,1>), они могут быть отфильтрованы и в конечном счете заменены небольшими вторжениями более кооперативных стратегий. Кооперативные стратегии, в свою очередь, будут свергнуты предающими стратегиями, и когда концентрация предателей окажется достаточно высокой, отказывающиеся участвовать «одиночки» смогут снова одержать верх. Добавление выбора «не играть» в эволюционную ДЗ позволяет избежать неблагополучного состояния всеобщего предательства, однако приводит к лишь чуть менее нежелательному исходу, в рамках которого популяция циклически проходит через состояния всеобщего неучастия. (Szabó and Hauert 2002 содержит хорошее описание данного явления.)

Среди стратегий, которые допускают зависимость от предыдущего взаимодействия, Батали и Китчер отдают предпочтение аналогу GRIM, который был назван ими Различающий Альтруист (далее РА). РА сотрудничает с любым игроком, ранее его не предававшим, за неимением же такового он отказывается от участия. Батали и Китчер показывают, что в группе пяти простых стратегий имеет место циклический паттерн, схожий с описанным выше: «антисоциальные» (ведущие к предательству) стратегии сменяются «асоциальными» (воздерживающимися от участия), а те, в свою очередь, сменяются «социальными» (РА), которые вновь сменяются «антисоциальными». В ходе анализа, тем не менее, им приходится заключить, что, если популяция ограничена данными пятью стратегиями, эволюция заставит их провести «большую часть их срока в состояниях высокого сотрудничества» (хотя не так много, как в «полностью опциональной» игре, где в каждом раунде соединяются в пару лишь те, кто точно оповещает о своей готовности участвовать). Утверждается, что симуляции с агентами, которым разрешаются любые стратегии, где ход зависит от двух предыдущих ходов его противника, дают этому грубое подтверждение. Здесь необходимо высказать предостережение. Пока еще не ясно, какие же стратегии лежат в основе сотрудничающих популяций в симуляциях, тогда как РА в действительности не является вариантом для агента, память которого распространяется лишь на две игры. Как ни странно, сообщается о несколько меньшей кооперативности полностью опциональной версии игры, чем полуопциональной (хотя в каждом случае, как и ожидалось, кооперативности значительно больше, чем в обычной ДЗ). Проявившиеся в итоге эволюционная динамика и меры кооперативности являются достаточно специфическими, так что сравнение с другими работами затруднительно. Несмотря на предостережения, можно все же сделать следующий вывод: опциональность участия предоставляет другое объяснение того обстоятельства, что всеобщий и неумолимый отказ от сотрудничества редко встречается в паттернах взаимодействия, которые иногда моделируются в качестве эволюционных ДЗ.

Пространственные ДЗ

В предыдущем разделе разбирался спорный аргумент, согласно которому сотрудничество в ДЗ рационально, если каждый игрок знает, что другой достаточно похож на него, чтобы выбрать тот же самый ход. Аналог этого аргумента в эволюционном контексте, очевидно, более убедителен. Если агенты не соединены попарно наугад, а скорее более склонны играть с другими, преследующими схожие стратегии, то с большей вероятностью будет возникать кооперативное поведение.

Есть как минимум три механизма, посредством которых достигается этот вид «ассоциации» игроков. Один такой механизм в эволюционных ДЗ был широко изучен под названием «пространственная ДЗ» (далее ПДЗ). Игроки расположены в некой «географической» конфигурации. Это может быть массив с прямоугольной границей, например, или окружностью, или поверхностью сферы, или поверхностью тора без границы. Из географической конфигурации для каждого игрока установлены два (возможно, тождественных) вида окрестности. Агенты встретят только тех, кто находится в их окрестности «взаимодействия», и эволюционная динамика учитывает только платежи тем, кто находится в их окрестности «сравнения». В общем случае задействованная эволюционная динамика является одной из «имитаций победителя» в пределах окрестности взаимодействия. (Так можно смоделировать либо представление о том, что каждого игрока захватывает его самый успешный сосед, либо идею, согласно которой каждый игрок принимает самую успешную стратегию из тех, что он наблюдает.) Поскольку и эволюция, и взаимодействие являются «локальными», игроки с большей вероятностью (после первого раунда) встретят тех, кто преследует стратегии, схожие с их собственными, в ПДЗ, нежели чем в обычной эволюционной игре. Помимо эффектов «ассоциации» нужно также иметь в виду, что на исход ПДЗ может повлиять динамика имитации победителя, вследствие чего

вымрут стратегии, которые могли выжить — и в конечном счете одержать верх — с динамикой репликатора, чаще используемой в обычных ЭДЗ.

Как водится, интересом к рассмотрению пространственных ДЗ мы обязаны Аксельроду. Четыре копии каждой из 63 стратегий, участвовавших в турнире Аксельрода, были размещены на сетке со сферической геометрией так, чтобы каждая ячейка имела четырех соседей как для взаимодействия, так и для сравнения. Для каждого начального равномерного распределения получающаяся ПДЗ в конечном счете достигла состояния, когда стратегия в каждой ячейке сотрудничает со всеми соседями, после чего дальнейшая эволюция не является возможной. В подобных конечных состояниях остались лишь около десяти из 63 исходных стратегий. Они уже были не равномерно распределены, но разделены на скопления различных размеров. Аксельрод также показал, что при особых обстоятельствах эволюция в ПДЗ может произвести последовательность сложных симметричных паттернов, которые, по-видимому, не достигают какого-либо устойчивого равновесия.

Чтобы понять, почему кооперативное поведение может распространиться в этой и подобных ей структурах, рассмотрим пример с двумя агентами, находящимися по разные стороны границы между сотрудничающими и несотрудничающими субпопуляциями. Кооперативный агент видит кооперативного соседа, чьи четыре соседа сотрудничают, вследствие чего после игры со всеми ими он получает четырехкратный платеж награды. Стало быть, агент будет подражать стратегии этого соседа и оставаться кооперативным. Несотрудничающий агент, напротив, видит своего кооперативного коллегу, который получает три платежа награды от кооперативных соседей и один платеж простака. Он сравнивает это с платежами своих некооперативных соседей. Лучшее, чего они могут добиться, — получить три наказания и искушение. Так, пока 3R+S превышает 3P+T, некооперативный агент на границе примет стратегию своего кооперативного соседа. Платежи Аксельрода 5, 3, 1 и 0 для T, R, P и S действительно отвечают этому условию.

Новак и Мэй более подробно разбирали ПДЗ, в которых единственными разрешенными стратегиями являются Cu и Du. (Подобные стратегии адекватны для людей, испытывающих недостаток памяти или навыков распознавания.) Они обнаружили, что для множества пространственных конфигураций и распределений стратегий эволюция зависит от относительных платежей единообразно. Когда платеж искушения достаточно высок, группы Du растут, а группы Cu сокращаются; когда он достаточно низок, группы Du сжимаются, а группы Cu растут. Для узкого диапазона промежуточных значений мы получаем последовательности сложных паттернов, схожих с теми, которые были отмечены Аксельродом. 

Развивающиеся паттерны демонстрируют большое разнообразие. Для данной пространственной конфигурации, однако, соотношение стратегии Cu к Du, по-видимому, приближается к одинаковому постоянному значению для всех начальных распределений стратегий и всех платежей искушения в пределах особого диапазона. Представление, в соответствии с которым эти симуляции частично объясняют живучесть явлений сотрудничества в природе, подвергалось сомнению на том основании, что симуляции допускают детерминистские (безошибочные) ходы и обновления. Но авторы сообщают о присутствии схожих явлений при разнообразии условий ошибки, хотя в этом случае для выживания сотрудничающих требуются более низкие относительные значения искушения, а уровень ошибки не может превысить определенный порог. (См. Mukherjii et al. 1996 и незамедлительный ответ Nowak et al. там же.)

Грим, Мар и Сен-Дени сообщают о множестве симуляций ПДЗ с более высоким разнообразием начальных стратегий. В целом их наблюдения подтверждают правдоподобную гипотезу, согласно которой кооперативные исходы более типичны в ПДЗ, нежели в обычных ЭДЗ. Во всех симуляциях, начинавшихся со всеми без исключения чистыми реактивными стратегиями Новака и Зигмунда (т.е. всеми стратегиями по типу R(y,p,q), описанному выше, где y, p, и q принимают значение 0 или 1), выжил лишь вариант ЗЗЗ — т.е. R(1,1,0). (Хотя другие исходы, включая тот, при котором Du является единственным выжившим, а Cu и ЗЗЗ перемешиваются, также очевидно возможны). В симуляциях, начинавшихся со всеми 64 возможными чистыми стратегиями, в которых ход может зависеть от предыдущих двух ходов противника, выжили смешанные популяции, задействующие целое множество стратегий, подобных ЗЗЗ. Они все отказываются от сотрудничества после двойного отказа (DD), хотя необязательно после единственного (CD или DC); сотрудничают после двойного сотрудничества, хотя необязательно после единственного; сотрудничают во втором раунде игры, хотя необязательно в первом. (Опять-таки, возможны и иные исходы.) В симуляциях, начинавшихся со многими (например, 100) равномерно распределенными образцами смешанных реактивных стратегий Новака и Зигмунда, как правило, одерживала верх R(.99,.1), которая является разновидностью щедрой ЗЗЗ с великодушием, чей коэффициент ниже половины великодушия ЩЗЗЗ. Симуляции, начинавшиеся со случайного отбора нескольких (к примеру, 8) подобных стратегий, обычно приходили к смешанному устойчивому или циклическому паттерну, в котором преобладала единственная версия щедрой ЗЗЗ со значительно большим великодушием, чем у ЩЗЗЗ. R(.99,.6), который в два раза более щедр, чем ЩЗЗЗ, являлся частым победителем.

Пространственные разновидности опциональной ДЗ были достаточно подробно исследованы в Szabó and Hauert 2002. Помимо прочего авторы выяснили, что для особого (промежуточного) диапазона платежей популяция агентов, играющих «чистые» стратегии на квадратной решетке, будет развиваться по направлению к уникальному равновесию, в котором присутствуют все три стратегии. Такая ситуация прямо противоположна непрерывным циклам в непространственных версиях эволюционной опциональной ДЗ, рассмотренным выше. Как и ранние наблюдения, данный вывод может помочь в объяснении того, как группа могла бы достигнуть какого бы то ни было состояния помимо всеобщего предательства, хотя вопрос о том, как она могла бы достигнуть состояния всеобщего сотрудничества, остался бы открытым.

«Географический» аспект ПДЗ нельзя принимать слишком буквально. Ведь социальные применения и, вероятно, даже многие биологические, по-видимому, не нуждаются в какой бы то ни было геометрической конфигурации. (Почему бы вместо сетки, где у каждого агента четверо или восемь соседей, не использовать структуру наподобие «сот», к примеру, где соседей шесть?) Интерес к ПДЗ, по всей вероятности, обусловлен тем, что мои «окрестности» взаимодействия и сравнения намного меньше, чем популяция в целом, даже если на ситуации никак не влияют нюансы физической географии. Тем не менее, ПДЗ-модели эволюции сотрудничества в конкретных геометрических конфигурациях предоставили нам привлекательные образы для рассмотрения. Некоторые из примеров доступны по ссылкам в конце настоящей статьи.

ДЗ и социальные сети

Один из способов представить идею относительно локального взаимодействия более реалистической для некоторых применений состоит в том, чтобы позволить агентам выбирать партнеров, основываясь на платежах в прошлых взаимодействиях. В Skyrms 2004 исследуются итерационные ДЗ среди популяции безусловно сотрудничающих и безусловно отказывающихся от сотрудничества. Первоначально, как обычно, каждый агент выбирает партнера случайным образом из остающихся членов популяции. Для последующих взаимодействий, однако, вероятность выбора того партнера устанавливается в соответствии с платежами предыдущих раундов, когда партнер был выбран, или (более реалистично) платежами предыдущих раундов, в рамках которых наличествовало взаимодействие с тем партнером (независимо от того, кто именно был «выбирающим»). В типовой ДЗ, где платежи искушения, награды, наказания и простака — 3, 2, 1 и 0, как сотрудничающие, так и отказывающиеся в конечном счете выбирают только сотрудничающих. По этой причине сотрудничающие играют чаще, чем отказывающиеся, которые играют только тогда, когда совершают выбор. Если мы допускаем, что доли сотрудничающих и отказывающихся равны, то сотрудничающие могут ожидать доход одного платежа награды, когда совершают выбор, или смесь платежей награды и простака один к одному, когда выбирают их. Таким образом, ожидаемый платеж для каждого взаимодействия равен (3R+S)/2. Отказывающиеся могут ожидать доход одного платежа искушения за игру, но они играют в два раза реже. С обозначенной структурой платежей 3R+S>T сотрудничающие добиваются большего успеха даже в условиях подобной «односторонней» ассоциации.

История может развернуться несколько по-другому в том, что Скирмс называет «ослабленной» ДЗ, где платежи составляют 2,01, 2, 1,98 и 0. (Мы могли бы назвать такую игру «Не окажись в простаках».) Здесь, как и прежде, сотрудничающие быстро учатся не выбирать в качестве партнеров отказывающихся от сотрудничества. Отказывающиеся получают примерно те же платежи, выбирают ли они в качестве партнеров сотрудничающих или отказывающихся. Так как сотрудничающие быстро прекращают их выбирать, однако, их доходы от взаимодействия с сотрудничающими будут меньше, чем доходы от отказывающихся, и они скоро станут выбирать лишь других отказывающихся. (Здесь важно понять, что алгоритм обучения, определяющий вероятность «я буду взаимодействовать с агентом a» зависит от общего дохода от взаимодействия с a (или общего количества недавних доходов от взаимодействия с a), а не от среднего дохода от взаимодействия с a. Так ослабленная игра завершается совершенной ассоциацией: отказывающиеся играют с отказывающимися, а сотрудничающие играют с сотрудничающими. Так как платеж награды несколько превышает платеж наказания, сотрудничающие вновь добиваются большего успеха, чем отказывающиеся.

Рассмотренные выше игры для социальных сетей в действительности не являются эволюционными ДЗ в описанном выше смысле. Паттерны взаимодействия развиваются, но стратегический профиль популяции остается неизменным. Естественно допустить, что и стратегии, и вероятности взаимодействия развиваются одновременно с распределением платежей. Доминирование популяции сотрудничеством или отказом (либо ни одним из них) при таких условиях зависит от множества факторов: стоимостей платежей, начального распределения стратегий, относительной скорости корректировок стратегии и вероятностей взаимодействия, а также других свойств указанных двух эволюционных динамик. В Skyrms 2004 содержится общий разбор таких игр и множество привлекательных примеров, однако автор не предоставляет нам (или же не стремится предоставить) ни исчерпывающее рассмотрение социально-сетевых ДЗ, ни тщательный анализ точных формулировок, которые бы должным образом моделировали конкретные явления. Многое остается неизвестным.

Стратегии нулевого детерминанта

В социально-сетевой игре агенты выбирают из популяции потенциальных противников; в версии ИДЗ, занимавшей Аксельрода, агенты должны играть с каждым другим членом популяции, в состав которой они входят. Исходное описание ИДЗ у Дрешера и Флуда, однако, касалось единственной пары игроков, которые неоднократно играют в ту же ДЗ. В краткой, но влиятельной статье пара выдающихся физиков, Уильям Пресс и Фриман Дайсон, недавно вновь привлекла внимание к этой исходной версии ИДЗ или, скорее, к ее бесконечно повторяющейся разновидности.

Назовем эту игру (бесконечной) ИДЗ с двумя игроками, или 2ИДЗ. В других версиях ИДЗ, где пары от большей популяции объединяются неоднократно, чтобы играть в игру, успешной является та стратегия, которая приносит хороший счет. «Хороший» может означать (в случае эволюции с репликаторной динамикой) по меньшей мере «выше среднего балла по популяции» или (в случае эволюции с имитационной динамикой) «столь же высокий, что и баллы множества самых успешных агентов в популяции». При таких условиях в конкретном раунде игры гораздо важнее поднять свой счет, нежели понизить очки противника. Аксельрод неоднократно (и не без основания) советовал участникам его турниров не быть завистливыми. В 2ИДЗ, однако, размер популяции равен двум игрокам. В этом случае понизить платеж вашего противника, чтобы поднять собственный, столь же ценно. Может даже оказаться более выгодным снижение своего платежа, если в результате платеж вашего противника окажется еще меньше.

Другое примечательное свойство 2ИДЗ (строго доказанное в Press and Dyson 2012: app. A), состоит в том, что для хорошей игры в ней не требуется длинная память. Предположим, что я принимаю однопамятную стратегию, т.е. обусловливаю каждый ход только нашим последним взаимодействием. Пресс и Дайсон показывают, что в таком случае вы не сможете извлечь выгоду при использовании более длинной памяти: безотносительно стратегии, которую вы принимаете, есть эквивалентная однопамятная стратегия, которую вы могли бы принять и которая принесла бы нам обоим то же самое количество очков. Принимая такую стратегию самостоятельно, я гарантирую, что более длинная память не будет иметь никакой выгоды для вас. Поэтому мы безо всякой потери общности можем рассматривать 2ИДЗ в качестве игры между агентами с однопамятными стратегиями.

2ИДЗ с однопамятными агентами (и в целом любая игра с двумя однопамятными участниками и двумя ходами) может быть представлена примечательно ясным образом. Пусть O1,O2,O3,O4 будут четырьмя исходами CC,CD,DC и DD. Однопамятные стратегии (как отмечено в обсуждении эволюции выше) — S(p1,p2,p3,p4) сотрудничества с вероятностью p1,p2,p3,p4 после исходов O1,O2,O3,O4. (Если мы допускаем, что игра повторяется бесконечно много раз и что 0<pi<1 для i=1,2,3,4, то начальный ход может игнорироваться.) Пусть S(p1,p2,p3,p4) и S(q1,q2,q3,q4) будут стратегиями первого и второго игроков соответственно. 

(Подстрочные индексы переключены для второго игрока так, чтобы p2 и q2 оба дали вероятность сотрудничества после получения платежа простака, а p3 и q3 — вероятность сотрудничества после получения искушения). Пусть p'i=1−pi и q'i=1−qi (для i=1,2) (так что p'i и q'i являются шансами отказа). Тогда мы можем представить 2ИДЗ между первым и вторым игроками как «переходную матрицу Маркова», которая определяет вероятность перемещения из одного состояния в другое.

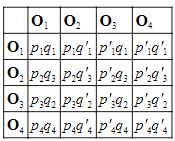
Например, вероятность перемещения из состояния O2, где первый игрок сотрудничает, а второй отказывается, в O4, где оба игрока предают, представлена во второй строке четвертого столбца: p'2q'3.

Такое рассмотрение игры позволяет применить аппарат матричной алгебры и цепей Маркова, что привело Пресса и Дайсона к установлению класса стратегий нулевого детерминанта (НД). (Более простое доказательство основного результата Пресса и Дайсона с использованием более скромного математического аппарата приводится в Hilbe et al. 2013: app. A.) В соответствии со стратегией НД игрок может обеспечить фиксированную линейную зависимость между своим долгосрочным средним платежом и платежом противника. Например, ЗЗЗ (=S(1,0,1,0)) оказывается подобной стратегией для любой ДЗ. Если я преследую ЗЗЗ, я гарантирую, что независимо от выбранной вами стратегии мы получим равный платеж. Если вы выбираете безусловное сотрудничество (=S(1,1,1,1)) или ЩЗЗЗ (=S(1,.25,1,.25)), мы получаем платеж награды; если вы выбираете безусловный отказ, мы приближаемся к среднему наказанию. Что касается остальных выборов, вы можете получить платеж между наказанием и наградой. Что бы вы ни выбрали, вы все равно получите тот же платеж, что и я.

Имеется целое множество стратегий НД для ИДЗ (и в целом для большинства игр с двумя ходами и двумя игроками). Для стандартной ДЗ с платежами 5, 3, 1, 0 тремя другими представительными стратегиями НД оказываются следующие:

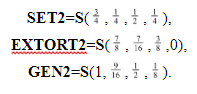
Пресс и Дайсон особо выделяют стратегии по типу SET2 и EXTORT2. Если первый игрок принимает SET2, тогда второй получит платеж 2 независимо от того, какой стратегии придерживается сам. В однопамятной 2ИДЗ игрок может приписать стратегии противника любое значение между платежами наказания и награды. В Hilbe et al. 2013 такие стратегии называются «уравнивающими», но в нашем контексте их уместнее было бы обозначить как «диктующие». Если первый игрок знает о диктующих стратегиях и знает, что второй игрок будет наивным максимизатором полезности, то первый сумеет обмануть второго, преследуя стратегию, подходящую ему за счет увеличения уровня, на котором он устанавливает платеж второго, когда недавняя игра последнего отвечает его желаниям. Конечно, более осведомленный второй игрок мог бы понять, что те же самые диктующие стратегии доступны и для него. Тем не менее, они окажутся бесполезными, если не приведут к изменению в поведении первого игрока. Если существование диктующих стратегий входит в общее знание этих двух игроков, то они могли бы с обоюдной выгодой согласиться установить друг другу платеж награды. Поскольку каждый преследует диктующую стратегию, ни один из них не сможет извлечь выгоду в ближайшей перспективе при отклонении. Если кто-либо отклоняется в надежде на долгосрочную выгоду, другой сумеет это обнаружить по изменению в платеже партнера или собственном платеже и затем предпринять ответное действие. Устойчивость такого соглашения, разумеется, зависит от того, смогут ли игроки сделать угрозы по применению ответных мер убедительными.

EXTORT2 является примером «вымогательской» стратегии НД. Если первый игрок принимает EXTORT2, тогда платеж V(2,1) второго всегда будет 2V(1,2)−1 (где V(1,2) является платежом первого). Второй игрок может, конечно, обеспечить себе по меньшей мере доход в 1 постоянным отказом. Однако вследствие линейной зависимости, которая связывает их платежи, если второй игрок добивается большего успеха, он обязательно проиграет первому. Действительно, любое приращение к счету второго игрока будет только половиной приращения противнику. В игре против наивного максимизирующего полезность противника EXTORT2 является даже более эффективной, чем SET2. Никакие уловки не требуются. Всякий раз, когда наивный противник получает больше, чем платеж наказания, он проигрывает вымогателю. Все, что он только делает, чтобы увеличить свой платеж, по необходимости увеличит доход вымогателя вдвое. Лучшее, что он может сделать против EXTORT2, так это безусловно сотрудничать. В итоге пара придет к результатам CC и DC в отношении три к одному,

средний платеж второго игрока составит 2,25, в то время как доход вымогателя составит 3,5. Единственная надежда второго игрока на спасение состоит в том, чтобы оставить максимизацию полезности и прийти к тому, что Пресс и Дайсон назвали «теорией сознания» (theory of mind). Если второй игрок поймет, что его действия могли бы заставить вымогателя отклониться от его стратегии, то он сумел бы сам принять вымогательскую стратегию. Это понизило бы оба их платежа в краткосрочной перспективе, но он мог бы надеяться на выгодные результаты в долгосрочной. Развязка, согласно Прессу и Дайсону, заключается в том, что в то время как стратегия вымогателя будет всегда побеждать наивного максимизатора полезности, 2ИДЗ с вымогателем и более смышленым агентом становится ультимативной игрой. Вымогатель предлагает несправедливое деление совместных платежей, которое оставляет его противника с неприятным вариантом принятия такого расклада или же приводит к неуспеху обоих. (Вероятно, следует отметить, что данный анализ исключает возможность того, что вымогающая сторона знает о платежах ее противника, равно как и своих, и, понимая, что ИДЗ разыгрывается только между двумя агентами, стремится минимизировать различие между собственным платежом и платежом противника. Принятие такой установки, по-видимому, привело бы к стратегии безусловного отказа. Платежи обоих игроков тогда приблизились бы к значению наказания — платеж вымогателя снизу, а жертвы вымогателя сверху.)

Ни диктующие, ни вымогательские стратегии, по всей видимости, не преуспевают в эволюционных играх с большими популяциями. По определению, успешные стратегии становятся более банальными в эволюционной структуре, и поэтому для них более вероятно смотреть на других, как на себя. Поскольку диктаторы и вымогатели не преуспевают против себя, любой успех, который они имеют в эволюционном контексте, подвергнется самоограничению. Эти интуитивные предположения были подтверждены в Hilbe et al. 2013. Авторы показывают, что когда весьма малая популяция общих однопамятных стратегий подвергается мутации и эволюции, время, которое агенты затрачивают на аппроксимацию стратегии НД, довольно велико в сравнении с количеством таких стратегий, которые являются возможными. Относительное время, затраченное на аппроксимацию стратегии диктатора, существенно больше, а относительные затраты времени на аппроксимацию вымогательской стратегии еще выше. Однако по мере увеличения размера популяции соотношение времени, затраченного на аппроксимацию всех трех категорий, быстро сокращается. Когда членов популяции более десяти, затраченное на эти стратегии время становится почти нулевым. На приблизительно том же самом уровне популяции средние компоненты x и z стратегий S(x,y,z,w) выживающих агентов (которые представляют вероятность сотрудничества после получения платежей награды и наказания) возрастают быстро, в то время как средние компоненты y и w уменьшаются медленно, так что в больших популяциях среднее число стратегий похоже на S(1,.9,.1,.1) — несовершенную версию P1. (Как можно было бы ожидать, по мере того, как среднее число стратегий приближается к P1, средний платеж увеличивается и приближается к значению награды. Отсюда следует, что при некоторых обстоятельствах известное нам представление, согласно которому сотрудничество более затруднительно среди больших групп, чем среди малых, ошибается с точностью до наоборот.)

Хотя вымогательские стратегии НД не слишком хорошо справляются в условиях эволюции, согласно Hilbe et al. 2013, они все же играют важную эволюционную роль как «катализаторы» эволюции сотрудничества. Авторы достаточно подробно исследуют направление эволюции агентов, ограниченных небольшим выбором стратегий, включая безусловный отказ, вымогательскую стратегию НД и уже знакомую нам (относительно кооперативную) стратегию P1. В отсутствие вымогателей безусловный отказ преобладает в популяции любого размера. При их наличии, однако, более успешной по мере увеличения размера популяции становится P1. Она преобладает в популяциях, где участников больше пятидесяти. Те же основные результаты сохраняются, когда в качестве стратегического выбора добавляется безусловное сотрудничество. В отсутствие вымогательских стратегий ЗЗЗ может играть схожую роль катализатора, позволяя P1 одержать верх над безусловным отказом (будь то при наличии безусловных сотрудничающих или в их отсутствие). Краткое объяснение состоит в том, что и ЗЗЗ, и вымогательские стратегии могут дрейфовать в популяцию безусловно отказывающихся в качестве нейтральных мутантов, при этом доля ЗЗЗ какое-то время может расти. В конечном счете, однако, большего успеха добьется P1, а не что-либо другое.

Следует отметить, что в Hilbe et al. 2013 отстаивается и применяется модель эволюции «попарное сравнение», которая заметно отличается от видов эволюционной динамики, расмотренных ранее в статье. На каждом этапе произвольно выбирается пара агентов, и первый принимает стратегию второго с вероятностью, которая увеличивается вместе с разницей их платежей. В условиях подобной динамики, если частота мутаций достаточно мала, популяция всегда будет двигаться к «фиксации», т.е. к состоянию, в котором каждый агент преследует одну и ту же стратегию. Время, необходимое для достижения фиксации, увеличивается с размером популяции, и если каждая стратегия получает одинаковые платежи в борьбе против кого-либо другого, то вероятность фиксирования стратегии s пропорциональна той части популяции, которая преследует s. Эти характеристики соответствуют знакомым свойствам в популяционной генетике, но они не проявляются, например, при репликаторной динамике.

В комментарии к статье, вводящей представление о стратегиях НД (Stewart and Plotkin 2012), указывается, что Пресс и Дайсон в значительной степени пренебрегают более щедрыми стратегиями НД по типу GEN2. Если первый игрок принимает GEN2 в 2ИДЗ с традиционной матрицей платежей, тогда платеж V(2,1) второго равен 2V(1,2)−3. Второй игрок в таком случае может позволить первому любой платеж между значением наказания 1 и значения награды 3, в то же время гарантируя себе еще больший платеж. Его самый высокий платежный ответ — Cu, который приводит к платежу награды 3 обоим игрокам. Стюарт и Плоткин сообщают, что стратегия по типу GEN2 фактически получает самый высокий балл среди девятнадцати стратегий на симулируемом турнире ИДЗ, схожем с турниром Аксельрода, который включает ЗЗЗ, ЩЗЗЗ, P1, GRIM и другие стратегии, побеждавшие ранее. Счет версии EXTORT2 предпоследний по списку. Важно заметить, что версия EXTORT2 заняла второе место по победам в состязаниях один на один, а версия GEN2 заняла четвертое с конца. Как подчеркивал Аксельрод в связи с ЗЗЗ, избиение противников на турнире ДЗ не ведет к успеху. Несмотря на всю свою привлекательность, замечания Стюарта и Плоткина оставляют открытым вопрос о том, является источником успеха стратегий по типу GEN2 их НД-характер или же нет.

В более поздней работе Stewart and Plotkin 2013 приводится доказательство, которое с некоторой оговоркой дает утвердительный ответ. Авторы опираются на детальное математическое исследование бесконечной ИДЗ, выполненное Этаном Акином. Акин (Akin 2013, Другие интернет-ресурсы) сосредотачивает внимание на стратегиях, которые точно отвечают желательным для нас условиям морально приемлемого «решения» 2ИДЗ: (1) их применение обоими игроками гарантирует кооперативный платеж; (2) оно также составляет равновесие Нэша, т.е. пару стратегий, дающих каждому игроку платеж, который он не может улучшить, отклоняясь от своей стратегии в одностороннем порядке; (3) наконец, оно предотвращает эксплуатацию — любая перемена в стратегии любого игрока, которая сокращает платеж его противника, также уменьшит его собственный платеж. Акин называет такие стратегии «хорошими» и выводит примечательно простое их описание. Стратегия S(p1,p2,p3,p4) хороша, если и только если она отвечает следующим условиям:

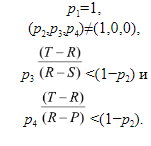
Легко убедиться, что со стандартными платежами ДЗ GRIM, ЗЗЗ, ЩЗЗЗ и GEN2 все отвечают этим условиям, в отличие от EXTORT2, SET2 и P1. (P1 отвечает условиям, когда платежи удовлетворяют R>12(T+P).)

Стюарт и Плоткин показывают, что хорошие стратегии, которые являются также стратегиями НД, — это в точности щедрые стратегии НД, т.е. подобные GEN2, которая уступает большую долю платежей между наказанием и вознаграждением противнику. Когда выводы исследования Hilbe et al. 2012 расширяются в применении до хороших стратегий и, в частности, щедрых стратегий НД, проявляющиеся паттерны оказываются совсем другими. В небольших популяциях стратегии тратят немного времени на эти стратегии в обозначенных двух группах (относительно шанса), а в больших популяциях они требуют намного больше времени. В больших популяциях очень высока доля стратегий, наиболее явно одобряемых эволюцией; таковы хорошие стратегии НД. Как бы то ни было, история не так проста. Стратегии, которые являются хорошими, но не НД, умеренно одобряются эволюцией, но несколько стратегий, которые не являются ни НД-стратегиями, ни хорошими, также весьма одобряются.

Нет сомнения, что идентификация стратегий НД вдохнула новую жизнь в исследования простых игр и, в частности, ИДЗ. Ее следствия, касающиеся эволюционных ДЗ и возникновения сотрудничества, поняты еще далеко не полностью.

Групповой выбор и модель стога сена в ДЗ

Третий механизм, с помощью которого игроков можно заставить с наибольшей вероятностью встретить похожих на себя, должен учитывать более сложную динамику эволюции, которая работает как в группах игроков, так и в отношении индивидов в пределах этих групп. Среди биологов и философов биологии велись жаркие дискуссии касательно того, что можно считать надлежащими «единицами [естественного] отбора». Представление, в соответствии с которым во многих случаях уместно принимать за эти единицы группы людей (а не гены или индивидов или не только их), недавно было возвращено к жизни и сочтено достойной и правдоподобной позицией. (См. его историю и ярую защиту в Sober and Wilson 1998 или Wilson and Sober 1994.) Эта идея также справедлива в отношении культурной эволюции — внутригрупповое поведение может находиться в равновесии, но равновесие, достигнутое различными группами, может быть разным. Менее успешные группы могут подражать более успешным, сменяться ими или отдавать им своих членов. Собер и Уилсон иногда отмечают, что если эволюционная теория игр является альтернативной точкой зрения на групповой отбор, то важно понимать, что это верно только для простых эволюционных моделей наподобие ранее представленных. Могут существовать и более сложные эволюционные игры. Рассмотрите, например, простую версию модели стога сена, первоначально описанную Джоном Мэйнардом Смитом. Пары игроков от большой популяции соединяются случайным образом. Каждая пара колонизирует один стог сена. Пара играет ДЗ, и платежи индивида определяют число его потомков в следующем поколении. (Родители умирают, когда рождаются дети.) На протяжении некоторого фиксированного количества поколений одни члены колонии соединяются в пары с другими случайным образом и играют в ДЗ.

Затем стоги сена разрушаются, популяция смешивается, а случайные пары колонизируют стоги сена следующего сезона. Один простой способ представить ДЗ стога сена с n поколениями, как мы могли бы назвать эту ДЗ, состоит в том, чтобы рассмотреть ее в качестве игры между двумя начальными основателями стога сена с таким платежом основателю, который равняется числу живущих потомков, использующих его стратегию. (Эта идея выдвигается в Bergstrom 2002 и излагается в Skyrms 2004). Например, предположим, что n=3 и что искушение, награда, наказание и простак составляют 5, 3, 1, 0. Тогда, если первый игрок сотрудничает, а второй предает, платеж первого составит 0, потому что сотрудничающий получает 0 потомков во втором и любом последующем поколении. Платеж второго игрока составит 5, поскольку предатель имеет пять (аналогично мыслящих) потомков среди второго поколения и каждый из них имеет по одному в третьем поколении, так как больше не остается сотрудничающих. Полная матрица платежа для четырех поколений ДЗ по типу «стог сена» с платежами 3,2,1 и 0 представлена ниже.

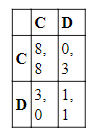
Как отметил Скирмс (Skyrms 2004), матрица описывает обычную охоту на оленя в определении, данном выше. Фактически, наблюдение Скирмса в общем случае верно. Для любой игры ДЗ g, если n достаточно велико, версия g по типу «стог сена» в поколении n является охотой на оленя. Простой аргумент в пользу этого утверждения приводится в следующем кратком дополнительном документе:

ДЗ «стоги сена» становятся охотами на оленя.

Библиография

Руссо, Жан-Жак, 1969, «Рассуждение о происхождении и основаниях неравенства между людьми», Трактаты, Москва, Наука.

Шеллинг, Томас, 2016, Микромотивы и макроповедение, Москва, Издательство Института Гайдара.

Юм, Дэвид, 1996, «Трактат о человеческой природе», Соч.: В 2 тт., Москва, Мысль, т. 1.

Aumann, Robert, 1995, “Backward Induction and Common Knowledge of Rationality,” Games and Economic Behavior, 8: 97–105.

–––, 1998, “Note on the Centipede Game,” Games and Economic Behavior, 23: 97–105.

Axelrod, Robert, 1981, “The Emergence of Cooperation Among Egoists,” The American Political Science Review, 75: 306–318.

–––, 1984, The Evolution of Cooperation, New York: Basic Books.

Axelrod, Robert and Douglas Dion, 1988, “The Further Evolution of Cooperation,” Science, 242 (December 9): 1385–1390.

Axelrod, Robert and William Hamilton, 1981, “The Evolution of Cooperation,” Science, 211 (March 27): 1390–1396.

Batali, John and Philip Kitcher, 1995, “Evolution of Altruism in Optional and Compulsory Games,” Journal of Theoretical Biology, 178: 161–171.

Becker, Neal and Ann Cudd, 1990, “Indefinitely Repeated Games: A Response to Carroll,” Theory and Decision, 28: 189–195.

Bendor, Jonathan, 1987, “In Good Times and Bad: Reciprocity in an Uncertain World,” American Journal of Political Science, 31: 531–558.

–––, 1993, “Uncertainty and the Evolution of Cooperation,” Journal of Conflict Resolution, 37: 709–733.

Bendor, Jonathan, and Piotr Swistak, 1995, “Types of Evolutionary Stability and the Problem of cooperations,” Proceedings of the National Academy of Sciences, 92 (April): 3596–3600.

Bendor, Jonathan, and Piotr Swistak, 1996, “The Controversy about the Evolution of Cooperation and the Evolutionary Roots of Social Institutions,” in Gasparski, Wojciech et al (eds), Social Agency, New Brunswick, N.J.: Transaction Publishers.

Bendor, Jonathan, and Piotr Swistak, 1997, “The Evolutionary Stability of Cooperations,” American Political Science Review, 91 (2): 290–307.

Bendor, Jonathan, and Piotr Swistak, 1998, “Evolutionary Equilibria: Characterization Theorems and Their Implications,” Theory and Decision, 45: 99–159.

Bendor, Jonathan, Roderick Kramer and Piotr Swistak, 1996, “Cooperation Under Uncertainty: What is New, What is True and What is Important?” American Sociological Review, 61 (April): 333–338.

Bergstrom, T., 2002, “Evolution of Social Behavior: Individual and Group Selection Models,” Journal of Economic Perspectives, 16: 231–238.

Bicchieri, Cristina, 1989, “Self-refuting Theories of Strategic Interaction,” Erkenntinis, 30: 69–85.

Binmore, Kenneth, 1992, Fun and Games, Lexington, MA: D.C. Heath and Company.

–––, 1994, Playing Fair: Game Theory and the Social Contract 1, Cambridge, MA: MIT Press.

–––, 1997, “Rationality and Backward Induction,” Journal of Economic Methodology, 4: 23–41.

–––, 2005, Natural Justice, New York, NY: Oxford Univsity Press.

Boyd, Robert and Jeffrey Lorberbaum, 1987, “No Pure Strategy is Evolutionarily Stable in the repeated Prisoner's Dilemma Game,” Nature, 327 (May 7): 58–59.

Carroll, J.W., 1987, “Indefinite Terminating Points and the Iterated Prisoner’s Dilemma,” Theory and Decision, 22: 247–256.

Cambell, Richmond and Lanning Snowden, 1985, Paradoxes of Rationality and Cooperation, Vancouver: University of British Columbia Press.

Danielson, Peter, 1992, Artificial Morality: Virtual Robots for Virtual Games, London: Routledge.

Davis, Laurence, 1977, “Prisoners, Paradox and Rationality,” American Philosophical Quarterly, 14: 319–327; reprinted in Campbell and Snowden, 45–58.

–––, 1985, “Is the Symmetry Argument Valid?,” in Campbell and Snowden 1985, 255–262.

Donninger, Christian, 1986, “Is It Always Efficient to be Nice?” in Dickman and Mitter (eds.), Paradoxical Effects of Social Behavior, Heidelberg: Physica Verlag, 123–134.

Farrell, Joseph, and Roger Ware, 1989, “Evolutionary Stability in the Repeated Prisoner's Dilemma,” Theoretical Population Biology, 36: 161–167.

Gauthier, David, 1986, Morals by Agreement, Oxford: Clarendon Press.

Grim, Patrick, Gary Mar and Paul St. Denis, 1998, The Philosophical Computer, Cambrige, Mass: MIT Press.

Hardin, Garret, 1968, “The Tragedy of the Commons,” Science, 162 (December 13): 1243–1248.

Hilbe, Christian, Martin A. Nowak, and Karl Sigmund, 2013, “Evolution of extortion in Iterated Prisoner's Dilemma games,” Proceedings of the National Academy of Sciences, 110 (17): 6913–6918.

Howard, Nigel, 1971, Paradoxes of Rationality, Cambridge, MA: MIT Press.

Howard, J.V., 1988, “Cooperation in the Prisoner's Dilemma,” Theory and Decision, 24: 203–213.

Hurley, S.L., 1991, “Newcomb's Problem, Prisoners' Dilemma, and Collective Action,” Synthese, 86: 173–196.

Joyce, James, 1999, The Foundations of Causal Decision Theory, Cambridge University Press.

Kavka, Gregory, 1983, “Hobbes War of All Against All,” Ethics, 93: 291–310.

–––, 1986, Hobbesean Moral and Political Theory, Princeton: Princeton University Press.

–––, 1991, “Is Individual Choice Less Problematic than Collective Choice?” Economics and Philosophy, 7: 291–310.

Kitcher, Philip, 1993, “The Evolution of Human Altruism” Journal of Philosophy, 90: 497–516.

–––, 2011, The Ethical Project, Cambridge, MA: Harvard University Press.

Kollock, Peter, 1993, “An Eye For an Eye Leaves Everybody Blind: Cooperation and Accounting Systems,” American Sociological Review, 58: 768–786.

Kraines, David and Vivian Kraines, 1989, “Pavlov and the Prisoner's Dilemma,” Theory and Decision, 26: 47–79.

–––, 1993, “Learning to Cooperate with Pavlov: an Adaptive Strategy for the Iterated Prisoner's Dilemma with Noise,” Theory and Decision, 35: 107–150.

Kreps, David, Paul Milgrom, John Roberts and Robert Wilson, 1982, “Rational Cooperation in the Finitely Repeated Prisoner's Dilemma,” Journal of Economic Theory, 27: 245–252.

Kuhn, Steven, 1996, “Agreement Keeping and Indirect Moral Theory” Journal of Philosophy, 93: 105–128.

–––, 2004, “Reflections on Ethics and Game Theory” Synthese, 141: 1–44.

Kuhn, Steven, and Serge Moresi, 1995, “Pure and Utilitarian Prisoner's Dilemmas” Economics and Philosophy, 11: 123–133.

Lewis, David, 1979, “Prisoner's Dilemma Is a Newcomb Problem,” Philosophy and Public Affairs 8: 235–240.

Linster, Bruce, 1992, “Evolutionary Stability in the Infinitely Repeated Prisoners' Dilemma Played by Two-State Moore Machines,” Southern Economic Journal, 58: 880–903.

–––, 1994, “Stochastic Evolutionary Dynamics in the Repeated Prisoners' Dilemma,” Economic Inquiry, XXXII: 342–357.

Maynard Smith, John, 1978, “The Evolution of Behavior,” Scientific American, 239: 176–192.

Molander, Per, 1985, “The Optimal Level of Generosity in a Selfish, Uncertain Environment,” Journal of Conflict Resolution, 29 (December): 611–619.

–––, 1992, “The Prevalence of Free Riding,” Journal of Conflict Resolution, 36 (December): 756–771.

Mukherji, Arijit, Vijay Rajan and James Slagle, 1996, “Robustness of Cooperation,” Nature, 379 (January 11): 125–126.

Nowak, Martin, and Robert May, 1992, “Evolutionary Games and Spatial Chaos,”Nature, 359 (October 29): 826–829.

Nowak, Martin and Karl Sigmund, 1992, “Tit for Tat in Heterogeneous Populations,” Nature, 355 (January 16): 250–253.

–––, 1993, “A Strategy of Win-stay, Lose-shift that Outperforms Tit-for-tat in the Prisoner's Dilemma Game,” Nature, 364 (July 1): 56–58.

Nowak, Martin, Robert May, and Karl Sigmund, 1995, “The Arithmetics of Mutual Help,” Scientific American, (June): 76–81.

Nozick, Robert, 1969, “Newcomb's Problem and Two Principles of Choice”, in N. Resher (ed.), Essays in Honor of Carl G. Hempel, Dordrecht: D. Reidel, 114–146; reprinted in Cambell and Snowden 1985, 107–132.

Orbell, John, and Robyn Dawes, 1993, “A ‘Cognitive Miser Miser’ Theory of Cooperative Advantage,” American Political Science Reveiw, 58: 787–800.

Orbell, John, and Robyn Dawes, 1993, “Social Welfare, Cooperators' Advantage and the Option of Not Playing the Game,” American Sociological Reveiw, 58: 787–800.

Pettit, Phillip, 1986, “Free Riding and Foul Dealing,” Journal of Philosophy, 83: 361–379.

Pettit, Phillip and Robert Sugden, 1989, “The Backward Induction Paradox,” Journal of Philosophy, 86: 169–182.

Poundstone, William, 1992, Prisoner's Dilemma New York: Doubleday.

Press, William and Freeman Dyson, 2012, “Iterated Prisoner's Dilemma Contains Strategeis That Dominate Any Evolutionary Opponent,” Proceedings of the National Academy of Sciences, 109: 10409–10413.

Quinn, Warren, 1990, “The Paradox of the Self-Torturer,” Philosophical Studies, 59: 79–90.

Rabinowicz, Wlodek, 1998, “Grappling with the Centipede: Defense of Backward Induction for BI-Terminating Games,” Economics and Philosophy, 14: 95–126.

Rosenthal, R., 1981, “Games of Perfect Information, Predatory Pricing, and the Chain Store,” Journal of Economic Theory, 25: 92–100.

Segal, Nancy and Scott Hershberger, 1999, “Cooperation and Competition Between Twins: Findings from a Prisoner's Dilemma Game,” Evolution and Human Behavior, 20: 29–51

Selten, Reinhard, 1975, “Reexamination of the Perfectness Concept of Equilibrium in Extensive Games,” International Journal of Game Theory, 4: 25–55.

–––, 1978, “The Chain-Store Paradox,” Theory and Decision, 9: 127–159.

–––, 1983, “Evolutionary Stability in Extensive Two-person Games,” Mathematical Social Sciences, 5: 269–363.

Sigmund, Karl, 1993, Games of Life: Explorations in Ecology Evolution and Behavior, Oxford: Oxford University Press.

Skyrms, Brian, 1990, The Dynamics of Rational Deliberation, Cambridge, MA: Harvard University Press.

–––, 1996, Evolution of the Social Contract, Cambridge, Cambridge University Press.

–––, 1998, “The Shadow of the Future,” in Coleman and Morris (eds.), Rational Commitment and Social Justice: Essays for Gregory Kavka, New York, Cambridge University Press.

–––, 2004, The Stag Hunt and the Evolution of Social Structure, Cambridge, Cambridge University Press.

Sobel, J.H., 2005, “Backward Induction Without Tears?,” in D. Vanderveken (ed.), Logic, Thought and Action, Berlin: Springer, 433–461.

–––, 1993, “Backward Induction Arguments: A Paradox Regained,” Philosophy of Science, 60: 114–133.

Sober, Elliott and David Sloan Wilson, 1998, Unto Others: The Evolution and Psychology of Unselfish Behavior, Cambridge, MA: Harvard University Press.

Stewart, Alexander and Joshua Plotkin, 2012, “Extortion and Cooperation in the Prisoner's Dilemm,” Proceedings of the National Academy of Sciences, 109: 10134–10135.

–––, 2013, “From Extortion to Generosity, Evolution in the Iterated Prisoner's Dilemm,” Proceedings of the National Academy of Sciences, 110: 15348–15353.

Sugden, R., 1986, The Economics of Rights, Cooperation and Welfare, New York, Basil Blackwell; 2nd edition, 2004, Basingstoke, UK: Palgrave MacMillan.

Szabó:, György and Christoph Hauert, 2002, “Evolutionary Prisoner's Dilemma Games with Optional Participation,” Physical Review E, 66: 062903.

Taylor, Michael, 1987, The Possibility of Cooperation, Cambridge: Cambridge University Press.

Trivers, Robert, 1971, “The Evolution of Reciprocal Altruism,” Quarterly Review of Biology, 46: 35–57.

Vanderschraaf, Peter, 1998, “The Informal Game Theory in Hume's Account of Convention,” Economics and Philosophy, 14: 215–247.

Williamson, Timothy, 1992, “Inexact Knowledge,” Mind, 101: 217–242.

Wilson, D.S. and E. Sober, 1994, “Reintroducing Group Selection to the Human Behavioral Sciences,” Behavioral and Brain Sciences, 17: 585–654.