математика

Поделиться статьей в социальных сетях:

в избранное

Санкт-Петербургский парадокс

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Первая публикация: 04.11.1998; основательная переработка: 17.06.2013 

Санкт-Петербургский парадокс основан на игре, где подбрасывается монета до того момента, пока не выпадает орёл. Общее количество подбрасываний $(n)$ определяет выигрыш, который высчитывается по формуле $\$2^n$. Таким образом, если орёл выпадает при первом же броске, выигрыш составляет $\$2^1 =\$2$ и игра заканчивается. Если же в первый раз выпадает решка, монетка подбрасывается еще раз. Если в этот раз выпадает орёл, выигрыш составляет $\$22$, то есть $\$4$, и игра завершается. Если же решка выпадает во второй раз, монетка подбрасывается еще раз. И так далее. Существует бесконечное множество возможных последовательностей, когда выпадает орёл после того, как несколько раз подряд выпадает решка. Вероятность последовательности n бросков $(P(n))$ высчитывается по следующей формуле: $\$1$ делится на $2^n$, и ожидаемый общий выигрыш после каждой последовательности вычисляется по формуле, где сумма выигрыша умножается на его вероятность. Следующая таблица отображает цифры для последовательности, где $n$ равняется от 1 до 10. 

Это лишь начало таблицы, которая может быть бесконечной. Математическое ожидание в игре – это сумма ожидаемого общего выигрыша всех последовательностей. Поскольку ожидаемый общий выигрыш каждой возможной последовательности составляет $\$1$, а их может быть бесконечное количество, данная сумма составляет бесконечное количество долларов. Разумный игрок (который ценит только деньги и чья жажда денег не зависит от удачи), вступит в игру, если и только если вступительный взнос окажется меньше математического ожидания. В игре, на которой основывается Санкт-Петербургский парадокс, любой конечный вступительный взнос меньше ожидаемого математического ожидания, выраженного в денежном эквиваленте. Таким образом, разумный игрок вступил бы в игру, каким бы большим ни оказался конечный вступительный взнос. Но кажется очевидным тот факт, что определенная цена окажется слишком высокой для разумного игрока. Многие соглашаются с мнением Хакинга (1980: 563), что «немногие из нас заплатили бы даже $25$ за участие в этой игре». Если это верно, и если многие из нас разумны, то с этим мнением что-то пошло не так. Парадокс впервые был обнаружен швейцарским математиком XVIII века Николаем Бернулли и опубликован его братом Даниэлем в Трудах Санкт-Петербургской академии (1738-й год, английский перевод от 1954-го года). Вот почему это явление и называется «Санкт-Петербургский парадокс».

Предел полезности

Мнение Бернулли об этом парадоксе состояло в том, что необходимо определить полезность (степень желательности или удовлетворения потребностей) выигрыша, выраженного в долларах. Мы остановимся на его подходе позже, а сейчас рассмотрим следующий (не его) вариант решения данной задачи. Допустим, человек достигает предела насыщения полезности, то есть в определенный момент дополнительная порция какого-либо блага не приносит наслаждения ни на каплю больше. Рассмотрим человека, который любит шоколадное мороженое, и каждая столовая ложка лакомства, съеденного им, приносит ему одинаковое удовольствие, равное одной единице полезности. Но когда он съел целую пинту мороженого (32 столовые ложки), он не может насладиться дополнительным, даже крошечным кусочком. Таким образом, 16 столовых ложек даёт ему 16 единиц полезности, а 32 столовые ложки – 32 единицы полезности. Но если бы он получил больше мороженого, он бы насладился лишь 32 столовыми ложками, то есть получил бы 32 единицы полезности. Теперь представим игру Санкт-Петербургского парадокса, где выигрыши такие же, как обозначены выше, но теперь они измеряются в столовых ложках шоколадного мороженого. Вот начало соответствующей таблицы единиц полезности: 

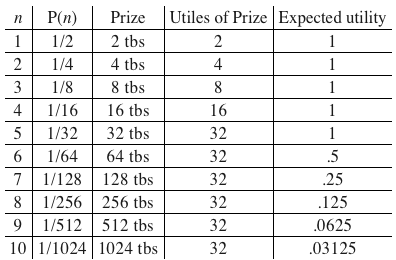
Теперь сумма в последней колонке не бесконечна: она асимптотически приближается к 6. В конечном итоге, игрок может ожидать средний выигрыш в размере 6 единиц полезности. Разумный любитель мороженого заплатил бы вступительный взнос в эквиваленте 6 столовых ложек шоколадного мороженого.

В качестве примера мы выбрали мороженое, потому что достижение максимума полезности данного вида может показаться менее невероятным, чем при участии прочих объектов. Сравним с первоначальным случаем, где платёж измеряется в долларах. Замена (Х долларов вместо Х столовых ложек) показывает максимальную полезность, которая достигается при выигрыше больше $32, а справедливый взнос за участие в игре составляет $6. Но применение максимальной величины означало бы, что $10 000 не стоит больше (при условии, что больше нет единиц полезности), чем $32. Однако никто так не думает. Итак, должны ли мы поднимать уровень, на котором у дополнительного доллара уже нет дополнительной ценности?

Лучше установить этот уровень на отметке (допустим) $17 млн.

Это настолько огромный выигрыш, что может показаться, что никакая сумма, превышающая его, не принесёт больше радости.

Между прочим, установка максимального уровня на этой отметке означает, что максимальный и разумный справедливый взнос за игру должен слегка превышать $25, что подтверждает интуитивное мнение Хакинга о рациональном максимальном взносе. Итак, именно ли это уровень, на котором полезность доходит до предела в денежном эквиваленте?

Мы уже определились, что это много денег и некоторым из нас потребуется недюжее воображение, чтобы определиться, что делать с суммой больше. Однако большинство людей, кажется, думает, что нет такого уровня, на котором дополнительный доллар буквально ничего не значит, то есть не представляет совсем никакой полезности. Кажется, желания в стиле «чем больше, тем лучше» вполне имеют право на существование, и даже довольно широко распространены.

Но это не означает, что математическое ожидание Санкт-Петербургского парадокса должно быть бесконечным. Есть возможности подойти к этому вопросу с таким предположением, что каждый дополнительный доллар приносит дополнительную полезность, но сумма бросков подряд не бесконечна. Первое подобное предположение высказал сам Бернулли.

Тот же документ, где математик раскрывает данную задачу, содержит первое опубликованное толкование «Принципа снижения предельной полезности», который он разработал для решения Санкт-Петербургского парадокса.

Данный принцип, который позже был широко принят в теории экономического поведения, устанавливает, что предельная полезность (полезность, полученная от потребления дополнительной доли блага) уменьшается по мере увеличения употребленного блага.

Иными словами, каждая дополнительная доля употребленного блага приносит меньше удовлетворения, чем предыдущая доля. Далее он утверждает, что реалистичную меру полезности денег можно высчитать через логарифм суммы. Ниже приведено начало таблицы игры, где единица полезности равна log($):

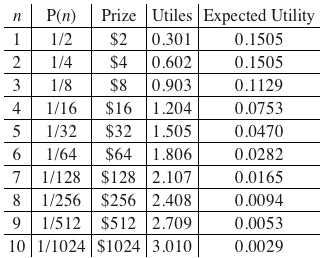
Сумма ожидаемых единиц полезности не бесконечна: она достигает предела на уровне 0,602 единиц полезности (что эквивалентно $4,00).

Это означает, что разумный игрок заплатил бы вступительный взнос в размере любой суммы, меньше $4,00.

Но не существует максимальной полезности любого результата: любой возможный результат в списке даёт больше полезности, чем тот, что находится выше.

Некоторым такой ответ на парадокс показался неудовлетворительным, поскольку Бернулли связывает полезность с логарифмом денежной суммы, что для многих выглядит ошибочным.

По его мнению, полезность, приобретенная удвоением какой-либо суммы денег, остается одинаковой.

Таким образом, разница в полезности $2 и $4 такая же, что и разница в полезности $512 и $1024.

Однако есть и другие способы понижения полезности, когда общая сумма растёт, что интуитивно может показаться более похожим на правду (см. работы Хардина от 1982-го года, Густасона от 1994-го года, Джеффри от 1983-го года). Главный фактор здесь заключается в том, что, если сумма единиц полезности в правой колонке достигает предела, то задача Санкт-Петербургского парадокса решена. Разумная сумма вступительного взноса – это любая сумма меньше данного предела. В своём классическом решении задачи Менгер (1967 [1934]) утверждает, что предположение о существовании высшего предела полезности чего-либо является единственным способом решения этого парадокса.

Однако снижение предельной полезности и её приближение к пределу могут не решить задачу.

Согласимся, что у денег есть понижающаяся предельная полезность, и допустим (в целях дискуссии), что разумный расчет полезности любой суммы в долларах выполняется через логарифм суммы в долларах. Тогда игра Санкт-Петербургского парадокса, как предполагается, не представляет никакого парадокса, однако можно с легкостью создать еще одну игру в стиле Санкт-Петербургского парадокса, которая действительно станет парадоксальной.

Для этого нужно лишь изменить выигрыши в долларах. Предположим, например, что вместо выплаты $2 в степени n за n бросков монетки, выигрыш составит $10 в степени 2 в степени n. Вот начало таблицы для такой игры:

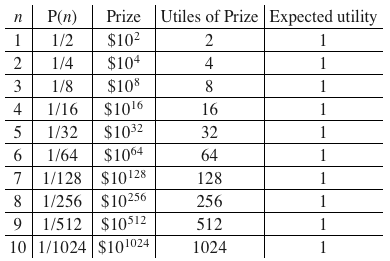
Математическое ожидание в этой игре – сумма бесконечных последовательностей цифр в последней колонке – бесконечное, а не просто очень большое. Это означает, что никакую сумму денег нельзя назвать слишком большой для вступительного взноса. Парадокс возвращается.

Логарифмическая функция Бернулли – не единственный способ соотнести ценность доллара с единицей полезности.

Существует еще и общее возражение им всем. Представим обобщенную игру Санкт-Петербургского парадокса (предложенную Полом Вейричем (1984: 194) вслед за Менгером (1967 [1934])), которая предлагает выигрыши в единицах полезности при коэффициенте 2 в степени n единиц полезности за n бросков (однако данное количество единиц полезности переводится в доллары или прочие блага). В этой игре было бы бесконечное математическое ожидание, и разумный игрок заплатил бы вступительный взнос любого размера, каким бы огромным он ни был.

Но можем ли мы сказать, что существует предел тому количеству единиц полезности, которое человек может употребить?

Создается впечатление, что не можем. Даже если полезность на единицу какого-либо определенного блага уменьшается с количеством, это не означает, что способность употреблять дополнительные единицы полезности уменьшается каким-либо образом. Если вас уже тошнит от мороженого, вы всё ещё можете наслаждаться музыкой Моцарта.

Нет такого закона, который бы предписывал уменьшение полезности единиц полезности. Чтобы стало проще, опустим обобщенную версию игры и продолжим обсуждать её в контексте оригинального выигрыша в долларах, при этом, однако, признавая, что уменьшающаяся предельная полезность долларов может внести изменения в выигрыши, необходимые для создания парадоксального результата.

Предотвращение риска

Рассмотрим следующее мнение. Игра Санкт-Петербургского парадокса предлагает возможность огромных выигрышей.

Например, последовательность из 40 выпадений решки подряд может привести к умопомрачительному выигрышу в размере $1,1триллиона. Конечно, такой выигрыш выпадает редко: только один раз из 1,1 триллионов.

В половине случаев выигрыш составляет лишь $2. Есть 75% возможности закончить игру с выигрышем $4 или меньше.

Шансы получить выигрыш больше $25 (именно эту сумму Хакинг называл разумным и максимальным вступительным взносом) меньше вероятности 1 к 25.

Очень низкие выигрыши очень вероятны, а очень высокие – очень редкие.

Глупым риском будут вложения в эту игру больше $25.

Размышления подобного рода вполне логичны и могут объяснить интуитивное мнение, соответствующее Хакингу. Многие из нас склонны избегать риск и не желают участвовать в игре с очень малыми шансами получить очень большой выигрыш.

Существует пара способов учёта этого избегания рисков.

Один из них – это встраивание его в функцию полезности, чтобы полезность, например, гарантированных $10 оказалась выше, чем полезность $20, которые можно выиграть с вероятностью в 50%.

Другой способ считает их одинаковыми, но добавляет отрицательную полезность беспокойства из-за априорной неопределённости. Вейрич (1984), утверждая, что учёт избегания риска решает Санкт-Петербургский парадокс, предлагает сложный способ (в который мы не будем здесь углубляться) включения фактора избегания риска в расчёт ожидаемой полезности с таким результатом, при котором существует конечный верхний предел разумного вступительного взноса в игру.

Но и этому подходу есть возражения. Прежде всего, избегание риска не является обычно применимым рассуждением при принятии разумных решений, поскольку некоторые люди не склонны избегать риск. Фактически, некоторые люди могут наслаждаться риском.

Что нам следует сказать о тех людях, которые, например, регулярно участвуют в государственных лотереях или играют в азартные игры в казино? (В таких играх вступительный взнос гораздо больше ожидаемой полезности).

Можно просто отвергнуть такое поведение как попросту нерациональное, но иногда такие игроки предлагают объяснение, что они наслаждаются волнением, испытываемым при риске.

Различия среди людей относительно их отношения к риску (и заодно относительно того, какое понижение предельной полезности денег они ощущают) можно изучить, допуская функции полезности, соответствующие индивидуальным особенностям каждого человека. Но в любом случае, совсем не очевидно, что избегание риска может объяснить, почему игра Санкт-Петербургского парадокса интуитивно воспринимается многими людьми, как игра со справедливо малым максимальным разумным вступительным взносом, хотя так много людей желают рисковать очень большими суммами денег ради огромных выигрышей, которые могут выпасть с гораздо меньшей вероятностью в других играх.

Но даже если мы предположим в целях дискуссии, что избегание риска приводит к интуитивному мнению, что подходящий вступительный взнос в игру Санкт-Петербургского парадокса является конечным и малым, это не устранит парадокс, поскольку мы опять же можем отрегулировать суммы выигрышей с учетом этого избегания рисков. Кажется вероятным, что люди, которые обычно не любят играть в азартные игры, вступили бы в данную игру, если бы выигрыш оказался достаточно большим.

Это доказывает факт, что гораздо больше людей участвуют в лотереях, когда те обещают большие выигрыши, несвойственные им ранее, при сохранении риска более или менее постоянным.

Однако, возможно, эти размышления не применяются ко всем аспектам игры Санкт-Петербургского парадокса. Если в этой игре есть бесконечная полезность, то даже очень большой вступительный взнос оправдан, а риск потерять эту сумму очень высок.

Самые убедительные примеры разумного непринятия риска при любой, даже очень большой сумме выигрыша, - это такие примеры, в которых вступительный взнос высок, а выигрыш маловероятен. Представим, например, что вы – человек, избегающий риск. Вас приглашают в игру, где вступительный взнос – все ваши пожизненные накопления (например, $100 000), а вероятность выигрыша составляет 1 к миллиону. Здесь отказ от игры выглядит разумно, каким бы огромным ни был возможный выигрыш.

Вероятно, именно это объясняет нежелание вкладывать большие деньги в игру Санкт-Петербургского парадокса.

Но обратим внимание, что это может оказаться недостаточным, неудовлетворительным ответом на этот парадокс.

Подобное избегание риска также предоставляет психологическое объяснение, почему (некоторые) люди отказываются играть на большие деньги, когда конечная ожидаемая полезность больше изначального взноса.

Таким образом, например, многие отказались бы рисковать одной тысячей долларов за выигрыш в размере $200 000, вероятность которого составляет 1 к 100 (математическое ожидание составляет $2 000). Если риск – это не отрицательная полезность, которую можно компенсировать увеличением выигрыша, то, возможно, поведение таких людей противоречит теории о математическом ожидании разумного выбора.

А если они разумны, то, возможно, это показывает, что теория неверна. Однако парадокс, который поднимает Санкт-Петербургская игра, не полностью изучается именно таким образом.

Это не просто случай (где прочие, подобные ему хорошо известны), в котором явно разумное поведение противоречит рекомендации максимизировать математическое ожидание. Парадокс здесь состоит в том, что его математическое ожидание бесконечно!

Конечное множество последовательностей

Густасон предполагает, что для избегания задачи Санкт-Петербургского парадокса следует ограничить законодательно разрешенные игры до (а) имеющих последовательности с верхним пределом значения (именно эту возможность мы и рассматривали) или (б) имеющих правила, где у каждого действия есть только конечное количество последовательностей.

Рассмотрим возможность второго ограничения.

Представим договор страхования жизни, приобретенный для кого-то с самого момента рождения.

Страховая компания выплачивает за имущество после смерти этого человека $100 за каждый день рождения, прожитый им, без ограничения. Какая цена должна быть у такого договора страхования?

Стандартные графики смертности, основанные на исследованиях, указывают шансы прожить еще один год при том или ином возрасте. Конечно, они не дают шанс прожить еще один год в возрасте 140 лет, поскольку не существует эмпирических доказательств этой возможности, но можно неопределенно выполнить разумное продление кривой смертности за пределы данных, предоставленных эмпирическими исследованиями. Эта кривая асимптотически спускается до нуля. На основе этого обычные математические вычисления могут показать математическое ожидание этого договора страхования.

Однако обратим внимание, что он обещает выплаты без каких-либо ограничений.

Если представить, что в каждом возрасте существует (большая или малая) вероятность прожить еще один год, то возникает бесконечно большое количество последовательностей, обязательных к рассмотрению при выполнении расчетов, но математика может вычислить предел этой бесконечной последовательности; и, (опуская прочие факторы) страховая компания получит свою прибыль, в конечном итоге, выставив цену договора выше данной суммы.

Математическое ожидание здесь вычислить совсем не сложно.

Это не «игра», конечно, но данная ситуация ставит под сомнение необходимость ограничения рассмотрения вероятностей и выплат случаями с конечным числом последовательностей.

Поскольку часто настаивают на том, что игра Санкт-Петербургского парадокса, как она описывается, не подпадает под рассуждения об обычных играх, внимательное рассмотрение требует изменений в механизме игры – изменения, которые мы бы ожидали, если бы данная игра действительно предлагалась в казино. Один способ осуществить это заключается в предположении, что механизм игры не проходил бы в точности так, как его описывают. Например, казино могло бы остановить игру после определенного количества выпадений решки подряд (назовём это количество N) и выплатить за N раз, даже если данная последовательность не завершилась выпадением орла. Тогда будет лишь конечное количество возможных последовательностей. Если N было бы установлено на 25, то математическое ожидание игры составило бы $25, и эта сумма и стала бы максимальным вступительным взносом, который разумный игрок согласился бы заплатить (что соответствует интуитивному предположению Хакинга). Предполагаем ли мы, возможно, бессознательно, что казино ограничили бы количество выпадений решки подряд до 25 раз? Почему именно 25?

Многие авторы отметили, что, практически говоря, должен быть некий предел количеству выпадений решки подряд без появления завершающего орла.

Во-первых, терпение участников игры должно когда-нибудь закончиться. Если может показаться, что это устанавливает слишком низкий предел числу N, рассмотрим значительно более высокий предел числу N, установленный на всю продолжительность жизни участников, или на длительность жизни всего человечества, или до того момента далёкого будущего, когда солнце взорвётся, испарив Землю.

Любой из этих пределов производит конечное математическое ожидание в игре, но при этом устанавливает число N, которое существенно выше 25. Что же тогда объясняет интуитивное предположение Хакинга о $25?

Более реалистичный предел числу N можно установить относительно конечности денежных средств, необходимых для поддержки игры. Любое казино, предлагающее игры, должно, как кажется, быть готовым к прекращению любой игры, если её продолжение будет стоить ему больше общей суммы денежных средств, доступных для выплаты выигрышей.

Последовательность из 25 бросков требовала бы выплату выигрыша в размере $33 554 432. Возможно, это приемлемо для крупного казино. Последовательность в 40 бросков требовала бы выигрыш в размере 1,1 триллионов долларов. Поэтому любое казино, предлагающее игру Санкт-Петербургского парадокса, должно ограничивать слишком большую последовательность бросков.

Может ли казино обойти эти практические трудности в соответствии с предположением Майкла Кларка (2002), что огромный выигрыш может быть предложен победителю только в качестве кредита? Поверит ли кто-нибудь такому обещанию? 

Разумеется, это верно, что какая-либо реальная игра установила бы определенный верхний предел числу N, производя конечное число возможных последовательностей игры. Но это не решает Санкт-Петербургскую задачу, поскольку эти конечные игры не являются Санкт-Петербургскими. Наш же вопрос касался игры Санкт-Петербургского парадокса, а не схожей с ней игры с ограниченным числом N. 

Парадокс брадобрея Рассела решается ответом, что искомого брадобрея попросту не существует. Могут ли реалистичные рассуждения решить Санкт-Петербургский парадокс, указав, что такой игры тоже не существует? Джеффри (1983: 154) утверждает, что «любой, кто предлагает игроку участвовать в игре Санкт-Петербургского парадокса, лжёт, поскольку притворяется, будто у него есть неопределенно большой денежный фонд».

Внося правки в идею, он представляет неопределенно большой банк правительства, способного печатать деньги по своему желанию, но указывает, что затем инфляция придаст конечность математическому ожиданию игры.

Если же кто-то, не имеющий поддержки правительства, создаёт впечатление, что предлагает эту игру, то Джеффри утверждает, что это предложение должно быть «иллюзорным»: на самом деле он предлагает не настоящую игру Санкт-Петербургского парадокса, а скорее её подобие, в котором будет установлен верхний предел выигрыша. 

Итак, это правда, что кто-либо, высказывающий это предложение, должен осознавать, что оно включает некоторые очень маловероятные последовательности, которыми этот человек не сможет управлять, но это не есть ложь.

Тот, кто не осознает, что его конечный финансовый резерв не может покрыть возможные последовательности, возможно, предлагает игру искренне, как и тот, кто понимает это, но берёт на себя риск задолжать победителю ту сумму, которую не сможет выплатить сразу.

Совет «Не делай такую ставку, которую не сможешь оплатить», иными словами, «Никогда не делай ставку без возможности выплатить самую большую сумму» имеет здесь смысл, поскольку иногда люди действительно делают слишком большие ставки. Ставка, сделанная в игре Санкт-Петербургского парадокса, не может быть покрыта, но при этом её могут предлагать со всей серьезностью.

Когда кто-то предлагает сделать ставку, но не выплачивает её, потому что не может, мы не приходим к выводу, что данное предложение было «иллюзорным». Мы настаиваем, что такое предложение является искренним. 

Возможно, точка зрения Джеффри действительно должна объяснить, почему люди (предположительно) не заплатили бы больше скромной суммы ($25?) за участие в игре. Потому что они бы не поверили, что им предлагают настоящую игру Санкт-Петербургского парадокса.

Однако это никоим образом не приближается к «Решению парадокса» (Название Джеффри, которое он дал данной части своей книги, стр. 154). Парадокс заключается в том, что настоящая Санкт-Петербургская игра обладает бесконечной привлекательностью и предлагает ставку, которая не может быть покрыта предложением человека. Тот факт, что мы не доверились бы тому, кто, видимо, высказывает нам данное предложение, ничего не решает. 

Средний выигрыш

Математическое ожидание – это действующая средняя окупаемость в конечном итоге. Рассмотрим график средних выигрышей при последовательности в простой игре, где мы получим $12, если выпадет 6, и не получим ничего при любом другом исходе.

По завершении первого раунда средний показатель выигрыша либо $12, либо $0.

По мере продолжения игры линия, отображающая средний показатель, будет идти вверх и вниз, но по мере увеличения количества раундов линия будет всё приближаться к $2.

Если стоимость каждого раунда $1 и проводится очень много раундов, можно рассчитывать на приближение к чистому выигрышу

(общий выигрыш минус стоимость участия в игре) в размере $1 за каждый раунд.

Какое-нибудь нестандартное казино, предлагающее эту игру, вероятно, будет терять сумму, близкую к $1 за каждый раунд, поскольку посетители играют в одну или сразу в несколько игр каждый.

Этот средний показатель в конечном итоге и является тем, что мы должны рассматривать при расчёте разумности участия в одной игре.

Почему средний результат соотносится с разумностью участия в одной игре – вот интересный философский вопрос о любом виде игры, и мы не будем останавливаться на нём здесь.

Но даже если каждый посетитель участвует только в одной игре, мы можем видеть, что в конечном итоге казино потеряет деньги, а его клиенты (как целая группа) приобретут. 

Можно ожидать, что линия графика средних выигрышей за последовательность бросков в этой игре в кости будет подниматься и опускаться с понижающейся амплитудой, сужаясь к отметке в $2.

Но линия графика последовательности в игре Санкт-Петербургского парадокса будет вести себя совершенно иначе.

Характерным образом она начинается с довольно низкого уровня.

В конце концов, за три четверти продолжительности игры общая сумма выигрыша составит либо $2, либо $4. Но с течением времени мы увидим внезапный и зрелищный скачок вверх, когда будет достигнут маловероятный, но огромный выигрыш. Затем линия графика будет постепенно понижаться, а далее прыгнет еще на моменте очередного огромного выигрыша.

Эти значительные прыжки будут встречаться всё реже и реже, но они повысят общую тенденцию графика. Типичный график предложен ниже (Хью, 2005). 

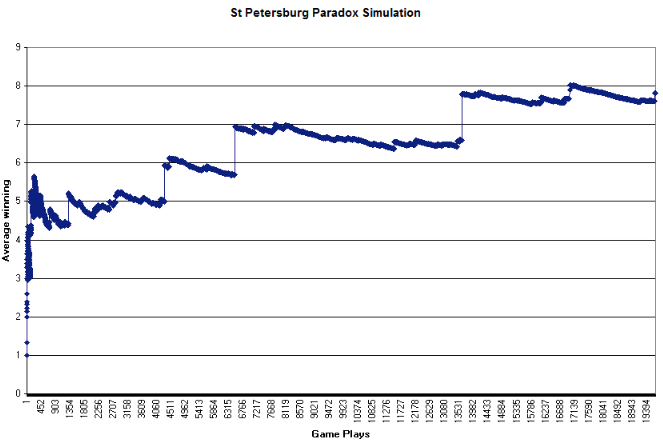
В отличие от графика игры в кости, график игры Санкт-Петербургского парадокса не приближается ни к какому пределу.

Чем дольше последовательность бросков, тем больше средний показатель выигрыша (грубо говоря).

Чем выше количество игр, в которых играют в казино, тем больше средняя выплата казино за каждую игру. В конечном итоге казино проиграет, а его посетители, как единая группа, выиграют, независимо от цены участия в игре. 

Всё вышесказанное есть лишь переработка того, о чем мы говорили ранее, просто с немного иной точки зрения.

Но этот способ восприятия вещей предполагает определенные выводы, которые ему соответствуют, и другие, которые не соответствуют. 

Во-первых, обратим внимание, что, если вы собираетесь принять участие в игре Санкт-Петербургского парадокса за достаточный вступительный взнос за каждую игру, вероятнее всего, вам придется играть очень-очень долго перед тем, как выйдете с положительным чистым выигрышем.

Подобным образом применяются обычные практические рассуждения, как мы видели, но в теории вы бы набрали чистый выигрыш, если бы продолжили игру достаточно долго. 

В этом отношении участие в игре Санкт-Петербургского парадокса скорее напоминает стратегию Мартингейла в азартных играх. Вот версия Мартингейла.

Заранее устанавливается желаемый уровень чистого выигрыша (выигрыш минус проигрыш). В первом раунде сделайте ставку, которая бы в случае выигрыша соответствовала вашей цели. Если вы выиграли, идите домой.

Если вы проиграли, в следующем раунде сделайте ставку, которая бы в случае выигрыша составила сумму вашего предыдущего проигрыша и целевого выигрыша.

Если вы выиграли, идите домой. Если проиграли, в следующем раунде сделайте ставку, которая в случае выигрыша составила бы сумму всех ваших проигрышей и целевого выигрыша.

Продолжайте эти действия до выигрыша.

Одна победа принесёт вам целевой чистый выигрыш. 

Данная стратегия Мартингейла всегда бы работала, если бы игра продолжалась достаточно длительное время. Но, разумеется, существуют практические трудности.

Возможно, вам придется играть очень долго перед первым выигрышем. Что еще хуже, при последовательности проигрышей сумма, необходимая для следующей ставки, растёт.

Сколько денег вам бы потребовалось, чтобы гарантировать успех в соответствии с Мартингейлом?

Сколько денег вы бы ни взяли с собой в казино, всегда остается вероятность, что их количества не будет достаточно для успешного осуществления стратегии Мартингейла. Схожим образом можно сказать, что, сколько денег ни было бы у казино, есть вероятность, что их не хватит на выплату победителю крупной суммы в игре Санкт-Петербургского парадокса. 

Итак, необходимо прояснить как Санкт-Петербургский парадокс, так и стратегию Мартингейла. При конечном и очень крупном денежном резерве игрок, осуществляющий стратегию Мартингейла, может с большой вероятностью победить, но есть и шанс, что у него закончатся деньги для вложения в игру перед выигрышем.

Практически говоря, игрок, выполняющий рекомендации Мартингейла, мог бы быть уверен в выигрыше, только если он мог бы быть уверен в том, что его денежный резерв продержится любое количество проигрышей подряд. А в этом он не может быть уверен.

Таким же образом при конечном очень огромном денежном резерве казино с большой вероятностью могло бы заработать, предлагая высокий вступительный взнос за игру Санкт-Петербургского парадокса, но есть вероятность, которая увеличивается с количеством раундов, что у казино окажется недостаточно денежных средств. 

Бесконечная сумма?

Иногда игре Санкт-Петербургского парадокса не уделяют должного внимания, потому что её математическое ожидание бесконечно, что означает, как утверждается, что эта игра не только попросту невозможна практически, но и теоретически неприемлема, находясь даже вне досягаемости умозрительного эксперимента. Но так ли это на самом деле? 

Представьте, что вам предложили следующую сделку. За договорную цену вы получите в постоянное владение кассовый аппарат со следующим необычным свойством: каждый раз, когда вы пробиваете на нём ту или иную сумму в долларах, кассовый аппарат выдаёт эту сумму.

Это не будет вычтено с вашего счёта и вам не придётся возмещать её позже.

Вы можете получать деньги из этого кассового аппарата так часто, как только захотите.

А теперь вопрос: сколько вы бы заплатили за этот кассовый аппарат? Вам кажется невозможным выполнить данный умозрительный эксперимент или найти ответ? Возможно, ваш ответ таков: вы готовы заплатить любую цену. При условии, что вы сможете отсрочить оплату первоначальной стоимости до подходящего момента, уже после приобретения кассового аппарата, потому что тогда вы сможете собрать любую необходимую для оплаты сумму денег из самого кассового аппарата. 

Конечно, возникают практические рассуждения: как долго вам бы пришлось собирать из кассового аппарата огромную сумму за его покупку?

Износится ли он или прекратится ваша жизнь, прежде чем вы соберёте всю сумму?

Любой банк был бы безумным, если бы согласился продавать вам кассовый аппарат с бесконечными деньгами (и, к сожалению, мы, кажется, потеряли адрес этого безумного банка, предлагающего такое оборудование).

Что же из этого? Главное здесь то, что в этом умозрительном эксперименте нет ничего, что невозможно было бы представить.

Он требует представить действие (приобретение кассового аппарата) при полном отсутствии верхнего предела математического ожидания. 

Кажется маловероятным, что ваша интуиция подскажет вам предложить, например, $25 в качестве предельной цены этого кассового аппарата.

Но единственная разница между ним и игрой Санкт-Петербургского парадокса в один раунд состоит в том, что кассовый аппарат гарантирует неопределенно большое количество выплат, а игра предлагает единовременную лотерею из неопределенно большого количества возможных выплат, каждая из которых обладает определенной долей вероятности.

Единственная разница между ними – это фактор вероятности. Та же разница существует между игрой, которая даёт вам гарантированный выигрыш в размере $5, и игрой, которая даёт вам $10 с долей вероятности в 50% и $0 с долей вероятности в 50%.

Математическое ожидание в игре Санкт-Петербургского парадокса и бесконечного кассового аппарата одинаково неопределенно велики. Вы бы предложили совершенно любую цену за любой из обоих объектов. Однако мы бы предположили, в реальной жизни, что предложение любого из них иллюзорно. Но, тем не менее, создается впечатление, что понятие бесконечного математического ожидания по меньшей мере подвластно размышлению. 

Разумеется, это понятие создает путаницу. Предположим, вы назначаете бесконечное значение за переход в рай. Бог говорит вам, что вы могли бы увеличить свои шансы, которые в данный момент равны нулю, на 1% за каждое доброе дело, совершаемое вами с настоящего момента.

Таким образом, ваш переход в рай будет твердо гарантирован после сотого доброго дела. Математическое ожидание при выполнении лишь одного доброго дела составляет .01 × ∞. Но это равняется математическому ожиданию при выполнении 100 добрых дел: 1.00 × ∞. Это означает, что вам лишь нужно один раз помочь старушке перейти дорогу, а затем вернуться к старому доброму эгоизму. Но этот вывод безумен. (Джеффри (1984: 153) предлагает подобный пример под названием De contemptu mundi”.)

Неограниченные параметры тоже могут внести путаницу в размышления о разумном выборе. Вот практический пример из реальной жизни. С момента своего появления домашние компьютеры становятся всё лучше и дешевле.

Следует ли вам купить новый прямо сейчас?

Нет, лучше довольствоваться имеющимся и подождать несколько месяцев, когда появятся компьютеры еще лучше и еще дешевле. Но при условии, что подобная ситуация никогда не изменится, ожидание всегда останется хорошей идеей, поэтому вы никогда не купите новый компьютер, каким бы хорошим и дешевым он ни оказался. Где же ошибка в этом рассуждении?

Мы можем избежать этого парадокса, привнеся некоторые «реалистичные» рассуждения, не обозначенные в данной истории, как и в случае с Санкт-Петербургским парадоксом. Но если мы не изменяем историю или не вводим дополнительные данные, из истории с компьютерами и из Санкт-Петербургского парадокса следуют безумные вещи. Вот почему две эти ситуации – парадоксы. 

Теория и практика

Игра Санкт-Петербургского парадокса –один из многих примеров, противоречащих стандартной (неограниченной) байесовской теории принятия решений. Каждый пример, как предполагается, является контр-примером теории по следующим причинам или по одной из них:

1. Теория в применении, предложенном примером, приводит к выбору, который люди на самом деле не делают или не сделали бы; таким образом, это описательно неверно.

2. Теория в применении, предложенном примером, приводит к выбору, который люди на самом деле не должны делать или который всецело, идеально разумный человек никогда бы не сделал; таким образом, это нормативно неверно.

Если вы считаете стандартную теорию нормативной, вы можете опустить возражения первого типа.

Люди не всегда разумны, а некоторые люди редко разумны, и верная описательная теория должна брать в расчет различные неразумные пути принятия решений. Неудивительно, что классическая, а скорее априористическая, теория не может быть описательно верной, и её критика на этой основе явно опускает её нормативную сторону. 

Возражения второго пункта следует рассмотреть более серьезно, и мы уже рассматривали ответы на Санкт-Петербургский парадокс как случаи именно этого вида.

Различные вариации «реалистичных» размышлений были приведены с целью показать, что результат, который предсказывает теория о поведении разумного игрока в Санкт-Петербургском парадоксе, неверен. Возникает вывод, что неограниченная теория ошибочна и что её необходимо ограничить для предотвращения парадокса. 

При рассмотрении правдоподобности ограничения расчётов математического ожидания различными способами с целью решить парадокс Амос Натан (1984: 133) обозначает, что необходимо помнить, что важное и менее свободное применение игр [с неограниченным математическим ожиданием] не имеет ничего общего с азартными играми и находится в физическом мире, где практические ограничения могут добавить совсем другое измерение. 

Натан не обозначает какое-либо физическое применение подобного расчета бесконечного математического ожидания. Но, тем не менее, остаётся правдоподобным предположение, что наложение ограничений на теорию для решения Санкт-Петербургского парадокса может привести к тому, что вместе с грязной водой мы выплеснем и ребенка. 

Любая теоретическая модель – это идеализация, что оставляет в стороне какое-либо конкретное практическое применение. «С математической и логической точек зрения, - размышляет Ресник (1987: 108), - Санкт-Петербургский парадокс непогрешим». Но с этой точки зрения мы оцениваем теорию как таковую (хотя это не единственная точка зрения на теорию).

По аналогии эстетическая оценка фильма не рассматривает такие факты, что единственный кинотеатр, показывающий фильм, находится очень далеко, а найти няню для ребенка на момент просмотра достаточно трудно. Если эстетическая теория говорит нам, что фильм прекрасен, но прочие рассуждения сообщают нам, что идти на него не следует, это не является дефектом эстетической теории.

Таким же образом математическая/логическая теория, объясняющая обыкновенные игры в казино, не имеет недостатков, поскольку она опускает практическую сторону, которая вмешивается в принятие решения в реальной азартной игре. Например, при решении о последующем шаге в покере: поднять ставку, пропустить ход или обналичить выигрыш и пойти домой –нужно принять во внимание, что сейчас пять утра, а вы уже окосели от усталости и алкоголя. Но эти материи нисколько не интересны математической теории, которая рассматривает лишь ценность ставки и возможность выигрыша. Дёринг и Фегер (2010: 93–94) видят теорию принятия решений как нормативную теорию об оценке действий при рассмотрении ожидаемой прибыли.

Соответственным образом, они утверждают, что «реализм», который привлекает практические рассуждения, например, ограничения реальной жизни на количество денег или времени, или возможность, что кто-нибудь вообще пригласит поучаствовать в этой игре, неуместен. 

Теория о принятии решений подобного вида утверждает, что никакую сумму нельзя назвать слишком большой для идеального, разумного и приемлемого вступительного взноса для участия в игре Санкт-Петербургского парадокса.

Это довольно странный результат, но он не приводит нас к выводу, что с теорией что-то не так. Мы лишь могли бы постараться принять этот странный результат. Как говорил Кларк (2002: 176): «Кажется, это один из тех парадоксов, который нам остаётся просто принять». 

Библиография 

Цитируемые работы

1. Bernoulli, Daniel, 1954 [1738], “Exposition of a New Theory on the Measurement of Risk”, Econometrica, 22: 23–36.
2. Clark, Michael, 2002, “The St. Petersburg Paradox”, in Paradoxes from A to Z, London: Routledge, pp. 174–177.
3. Döring, Sabine and Fretz Feger, 2010, “Risk Assessment as Virtue”, in Emotions and Risky Technologies (The International Library of Law and Technology 5), Sabine Röser, ed, New York: Springer, 91–105.
4. Gustason, William, 1994, Reasoning from Evidence, New York: Macmillan College Publishing Company.
5. Hacking, Ian, 1980, “Strange Expectations”, Philosophy of Science, 47: 562–567.
6. Hardin, Russell, 1982, Collective Action, Baltimore: The Johns Hopkins University Press.
7. Jeffrey, Richard C., 1983, The Logic of Decision, Second Edition, Chicago: University of Chicago Press.
8. Menger, Karl, 1967 [1934], “The Role of Uncertainty in Economics”, in Essays in Mathematical Economics in Honor of Oskar Morgenstern (ed. Martin Shubik), Princeton: Princeton University Press.
9. Nathan, Amos, 1984, “False Expectations”, Philosophy of Science, 51: 128–136.
10. Resnik, Michael D., 1987, Choices: An Introduction to Decision Theory, Minneapolis: University of Minnesota Press.
11. Weirich, Paul, 1984, “The St. Petersburg Gamble and Risk”, Theory and Decision, 17: 193–202.

Другие дискуссии

1. Arntzenius, Frank, Adam Elga, and John Hawthorne, 2004, “Bayesianism, Infinite Decisions, and Binding,” Mind, 113: 251–283
2. Ball, W. W. R. and H. S. M. Coxeter., 1987, Mathematical Recreations and Essays, 13th ed., New York: Dover.
3. Bernstein, Peter, 1996, Against The Gods: the Remarkable Story of Risk, New York: John Wiley & Sons.
4. Cowen, Tyler and Jack High, 1988, “Time, Bounded Utility, and the St Petersburg Paradox”, Theory and Decision: An International Journal for Methods and Models in the Social and Decision Sciences, 25: 219–223.
5. Gardner, Martin, 1959, The Scientific American Book of Mathematical Puzzles & Diversions. New York: Simon and Schuster.
6. Kamke, E, 1932, Einführung in die Wahrscheinlichkeitstheorie. Leipzig: S. Hirzel.
7. Keynes, J. M. K., 1988, “The Application of Probability to Conduct”, in The World of Mathematics, Vol. 2 (K. Newman, ed.), Redmond, WA: Microsoft Press.
8. Kraitchik, M., 1942, “The Saint Petersburg Paradox”, in Mathematical Recreations. New York: W. W. Norton, pp. 138–139.
9. Todhunter, I., 1949 [1865], A History of the Mathematical Theory of Probability, New York: Chelsea.