математика

Поделиться статьей в социальных сетях:

в избранное

Курт Гёдель

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 13 февраля 2007 года; содержательно переработано 11 декабря 2015 года.

Курт Фридрих Гёдель (1906–1978) был одним из главных основоположников современной метаматематической эпохи в математической логике. Он широко известен прежде всего своими теоремами о неполноте, которые относятся к числу значительных разделов математики XX века, но его работа коснулась также каждой области математической логики, даже если в большинстве случаев он не стоял у их истоков. В своих философских трудах Гёдель сформулировал и отстаивал математический платонизм, в соответствии с которым математика представляет собой сугубо описательную науку, — иными словами, представление о том, что понятие математической истины объективно. Опираясь на него, Гёдель заложил основу программы концептуального анализа в теории множеств (см. ниже). В математике Гёдель придерживался «оригинальной рационалистической концепции» Гильберта (как он ее называл) и был в некотором смысле провидцем, поскольку сумел предвосхитить и подчеркнуть важность больших кардинальных чисел в теории множеств еще до того, как их значение стало очевидным.

Биографический очерк

Курт Гёдель родился 28 апреля 1906 года в австро-венгерском городе Брюнн (в настоящее время — Брно в Чешской Республике).

Отец Гёделя Рудольф Август был коммерсантом, а его мать Марианна была высокообразованной и культурной женщиной, с которой Гёдель оставался близок на протяжении всей жизни, о чем свидетельствует долгая и обширная переписка между ними. Семья была успешной, и детство Гёделя было весьма однообразным за одним важным исключением, а именно: примерно с четырехлетнего возраста Гёдель часто болел, и проблемы со здоровьем, которые он испытывал, а также прочие негативные обстоятельства сопровождали его всю жизнь.

Несмотря на проблемы со здоровьем, Гёдель оказался образцовым учеником в начальной школе, а затем в гимназии, особенно в области математики, языков и религии. После окончания гимназии в Брно в 1924 году Гёдель поступил в Венский университет, где посещал лекции по физике, изучая область своих изначальных интересов, лекции по философии Генриха Гомперца и лекции по математике. Во времена студенчества Гёдель прослушал ряд курсов физики, о чем свидетельствует его приложение к диплому; это примечательно в связи с последующим вкладом Гёделя в теорию относительности в 1947 году. Филипп Фуртвенглер, двоюродный брат великого немецкого дирижера Вильгельма Фуртвенглера, был одним из его профессоров математики, и, конечно же, курс Фуртвенглера по теории поля фактически вынудил Гёделя продолжить занятия по теме. Гёдель изучал логику у Рудольфа Карнапа и Ханса Хана, и в конечном итоге под руководством Хана в 1929 году получил степень доктора философии в области математики. Основной темой его диссертации была теорема о полноте для логики первого порядка (Gödel 1929). 

Университетские годы Гёделя также ознаменовали начало его участия во встречах Венского кружка — сплотившейся вокруг Морица Шлика группы, которая вскоре стала известна как «логические позитивисты», термин, придуманный Фейглом и Блумбергом в их манифесте 1931 года «Логический позитивизм: новое течение в европейской философии» (Feigl and Blumberg 1931). Хотя Гёдель сам по себе не был логическим позитивистом, эти дискуссии оказали на него жизненно важное формирующее влияние. 

1930-е годы стали для Гёделя блистательным десятилетием. После публикации в 1930-м своей диссертации 1929 года он опубликовал свои основополагающие теоремы о неполноте в 1931-м, на основании которых в 1932-м ему была присуждена хабилитация, а в 1933-м он получил должность приват-доцента в Венском университете.

Среди его математических достижений на рубеже десятилетия — доказательства непротиворечивости как аксиомы выбора, так и континуум-гипотезы Кантора с аксиомами Цермело–Френкеля для теории множеств, полученные в 1935 и 1937 годах соответственно. Гёдель также опубликовал ряд важных статей по модальной и интуиционистской логике и арифметике в течение этого периода, главной из которых является его работа «Об интуиционистской арифметике и теории чисел» (Gödel 1933), в которой он показал, что классическая арифметика первого порядка интерпретируется в арифметику Гейтинга простым переводом. Другие публикации 1930-х годов затронули проблему разрешимости для исчисления предикатов, длину доказательств, а также дифференциальную и проективную геометрии.

К концу десятилетия научный руководитель Гёделя Ханс Хан и Мориц Шлик скончались (последний был убит бывшим его студентом). Эти два события привели Гёделя к личному кризису. Кроме того, его деятельность в университете в качестве приват-доцента была изменена на позицию доцента нового порядка (Dozentur neuer Ordnung), предоставляемую кандидатам только после установления расовой принадлежности. Три поездки Гёделя в США в течение 1930-х инициировали расследование. (См. Sigmund 2006.) Наконец, в 1939 году Гёдель был признан годным к военной службе нацистским правительством.

Данные события сыграли решающую роль в его решении покинуть Австрию в 1940 году, когда Гёдель вместе с супругой Адель в конечном итоге эмигрировали в Соединенные Штаты. Этот длинный и сложный эпизод в их жизни описан Джоном Доусоном в биографии Гёделя под названием «Логические дилеммы» (Dawson 1997), а также Соломоном Феферманом в «Жизни и работе Гёделя» (Feferman 1986), к которым мы отсылаем читателя.

По прибытии Гёдель принял назначение в качестве ординарного члена в Институте перспективных исследований; он станет постоянным членом Института в 1946 году и получит профессуру в 1953-м. (Гёдель и его супруга получили американское гражданство в апреле 1948-го.) Он оставался в Институте до выхода на пенсию в 1976-м. В Европу Гёдель больше не возвращался.

Ранние годы Гёделя в Институте отличились его тесной дружбой с повседневным спутником по прогулкам Альбертом Эйнштейном, а также его поворотом к философии математики, области, на которой Гёдель начал сосредотачиваться почти исключительно с 1943 года. Начальный период его последующей пожизненной деятельности в философии был исключительно плодотворным (с точки зрения публикаций): в 1944-м он опубликовал свою первую философскую статью под названием «Расселовская математическая логика» (Гёдель 1944), а через три года вторую — «Что такое континуум-гипотеза Кантора?» (Gödel 1947). В 1949-м он опубликовал третью работу («Замечание о взаимосвязи теории относительности и идеалистической философии», Gödel 1949a). Последняя статья совпала с результатами о вращающихся вселенных в теории относительности, полученными им в 1949 году, которые были впервые опубликованы в статье под названием «Пример нового типа космологических решений полевых уравнений гравитации Эйнштейна» (Gödel 1949).

К другим значимым философским трудам Гёделя 1940-х годов следует отнести его лекцию «В каком смысле интуиционистская логика является конструктивной?» (Gödel *1941), в которой вводится понятие «вычислимая функция конечного типа». Статья, которая опиралась на идеи его лекции «О еще неиспользованном расширении конечной точки зрения» (Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes), была опубликована только в 1958-м, а интерпретация арифметики Гейтинга в бескванторном исчислении T в ней стала впоследствии называться «интерпретацией „Диалектики“» в честь журнала Dialectica, где была опубликована статья (Gödel 1958). (Пересмотренную редакцию статьи от 1972 года см. в Gödel 1995.) Наконец, в течение этого десятилетия началось интенсивное изучение Гёделем Лейбница, которое, по сообщениям Гёделя, заняло период с 1943 по 1946 годы.

В 1950-е годы Гёдель все глубже вовлекался в философию. Гёдель выступил с философской лекцией в Университете Брауна, которую обычно называют Гиббсовской лекцией («Некоторые основные теоремы в основаниях математики и их следствия», Гёдель 1951). С 1953 по 1959 годы Гёдель работал над статьей для посвященного Рудольфу Карнапу сборника Шильппа под названием «Является ли математика синтаксисом языка?» (Gödel 1953). Он не опубликовал при жизни ни одной из этих двух важных рукописей, хотя обе они появились в двух списках, которые были обнаружены в «Наследии Гёделя», озаглавленном «Was ich publizieren könnte». («Что я смог опубликовать». Обе рукописи в конечном итоге появились в Gödel 1995.) К концу десятилетия Гёдель проявил серьезный интерес к феноменологии Эдмунда Гуссерля.

Последние годы Гёделя отмечены тиражированием двух его рукописей: «Некоторые соображения, приводящие к вероятному выводу о том, что истинная мощность континуума составляет ℵ2» (Gödel *1970a, *1970b), — попытка вывести значение континуума из так называемых аксиом масштаба Хаусдорфа; «Онтологические данные» (Gödel *1970), которую он доверил Дане Скотту в 1970 году (хотя, похоже, они были созданы ранее). Взятые вместе, две рукописи представляют собой подходящие заключительные ремарки для того, кто в течение пятидесяти лет занимался математикой и философией, преследовал или, точнее, искал основания для сосредоточения внимания на этих двух предметах в рамках единого понятия: «строгой науки» (strenge Wissenschaft) — воззрения, которым руководствовался Гёдель в 1929 году, когда в возрасте двадцати трех лет он начал свою докторскую диссертацию с некоторых философских замечаний.

Гёдель скончался в Принстоне 14 января 1978 года в возрасте 71 года. В его свидетельстве о смерти в качестве причины смерти указаны «голод и истощение вследствие расстройства личности». Его жена Адель пережила его на три года. 

Дополнительные биографические материалы см. в Gödel 1987, Kleene 1987, Kreisel 1980, Taussky-Todd 1987 и Yourgrau 2005.

Математическая деятельность Гёделя

Ниже приведена оценка некоторых из главных вкладов Гёделя в теорию множеств и логику. Настоящий анализ формальных работ Гёделя не является исчерпывающим, в частности, мы обходим вниманием деятельность Гёделя в области физики и его труды по проблеме разрешимости. Они будут рассмотрены в дальнейших статьях.

Полная хронология работ Гёделя приведена Джоном Доусоном в первом томе англоязычного собрания сочинений Гёделя (Gödel 1986: 37).

Теорема о полноте

Введение

Вопрос о полноте исчисления предикатов первого порядка был поставлен в точной форме и впервые опубликован в 1928 году Гильбертом и Аккерманом в работе «Основы теоретической логики» (Гильберт, Аккерман 1928), с текстом которой Гёдель был достаточно знаком.

Вопрос, поставленный Гильбертом и Аккерманом, заключается в том, является ли определенная эксплицитно заданная система аксиом для исчисления предикатов первого порядка «полной в том смысле, что из нее можно вывести все логические формулы, верные для каждой области объектов…» (van Heijenoort 1967: 48).

Доказательство теоремы полноты

Мы приводим краткое изложение собственного доказательства Гёделя в его докторской диссертации (Gödel 1929). Существенное отличие от предыдущих усилий (обсуждаемых ниже и в других местах, см., напр., Zach 1999) заключается в том, что Гёдель тщательно определяет все основные соответствующие понятия.

«Логическое выражение» в терминологии Гёделя — это правильно построенная формула первого порядка без тождества. Выражение «опровержимо», если его отрицание доказуемо, «общезначимо», если истинно во всех интерпретациях, и «выполнимо», если оно истинно в некоторой интерпретации. Теорема о полноте гласит:

Теорема 1. 

Каждое общезначимое логическое выражение доказуемо. Эквивалентно: каждое логическое выражение является либо выполнимым, либо опровержимым. 

Доказательство Гёделя основано на тексте Гильберта и Аккермана. Принято, что выражение представлено в нормальной форме, если все кванторы стоят в начале. Степень выражения или формулы — это число чередующихся блоков кванторов в начале формулы, которые по допущению начинаются с кванторов всеобщности. Гёдель показывает, что если теорема о полноте справедлива для формул степени k, то она должна выполняться для формул степени k + 1. Таким образом, вопрос о полноте сводится к формулам степени 1. То есть следует показать, что любая нормальная формула (Q)φ степени 1 является либо выполнимой, либо опровержимой, где «(Q)» обозначает (непустой) блок кванторов всеобщности, за которым следует (возможно, пустой) блок кванторов существования.

Гёдель определяет систему учета, предполагающую идеальную упорядоченность всех кортежей переменных, что обусловлено необходимостью соответствовать φ, как этого требует (Q). Например, если (Q)φ представляет собой ∀x0∃x1ψ(x0, x1), мы перечисляем бескванторные формулы ψ(xn, xn+1). (Или, точнее, их конечные конъюнкции возрастающей длины; см. ниже.) Тогда в любой области, состоящей из значений различных xn, в которых каждое ψ(xn, xn+1) истинно, предложение (Q)φ очевидно истинно. Важнейшая лемма утверждает, что для каждого k доказуема формула (Q)φ → (Qk)φk, где бескванторная формула φk утверждает истинность ψ для всех кортежей до k-го кортежа переменных, возникающих из (Q), и (Qk)φk — экзистенциальное замыкание φk. (Ниже см. пример, где дается определение φk). Эта лемма является основным шагом, который отсутствует в различных предыдущих попытках доказательства, предпринятых Лёвенгеймом и Скулемом, и в контексте теоремы о полноте для логики первого порядка делает связь между синтаксисом и семантикой выраженной полностью эксплицитно.

Рассмотрим пример того, как определенная формула окажется или выполнимой, или опровержимой, по методу Гёделя. Рассмотрим φ = ∀x0∃x1ψ(x0, x1), где ψ(x0, x1) бескванторна. Мы покажем, что либо она выполнима, либо доказуемо ее отрицание. Мы вводим следующие определения:

φ0 является выражением ψ(x0, x1)

φ1 является выражением ψ(x0, x1) ∧ ψ(x1, x2)

…

φn является выражением ψ(x0, x1) ∧ …∧ ψ(xn, xn+1).

Важная лемма, о которой говорилось выше, показывает, что из φ для каждого n можно вывести ∃x0…∃xn+1φn. 

Случай 1: φn не выполнимо для некоторых n. Тогда, прибегая к уже известной теореме о полноте для логики высказываний, Гёдель утверждает, что ¬φn доказуемо, а значит, и ∀x0,…, xn+1¬φn. Таким образом, ¬∃x0…∃xn+1φn доказуемо и, следовательно, ¬φ доказуемо, то есть φ в системе Гильберта — Аккермана опровержимо. (Некоторые частичные результаты, касающиеся пропозициональной логики, в дополнение к уже упомянутым включают в себя семантическую полноту исчисления высказываний (Post 1921), а также более общую теорему о полноте по Бернайсу; последняя появляется в неопубликованной докторской диссертации Бернайса 1918 года, см. также Bernays 1926.)

Случай 2: Каждое φn выполнимо. Существует только конечное число возможных моделей с универсумом {x0,…, xn+1}. Гёдель упорядочивает их как дерево, определяя модель М ниже модели М', если М является подмоделью М'. Таким образом, мы получаем дерево, которое конечно разветвляется, но само бесконечно. Согласно лемме Кёнига, существует бесконечная ветвь B. (В доказательстве Гёдель эксплицитно строит ветвь, заданную леммой Кёнига, а не просто отсылает к ней.) Объединение моделей на B образует модель M с универсумом {x0, x1,…}. Поскольку M удовлетворяет каждому φn, то исходная формула φ действительна в M. Следовательно, φ выполнимо, что и требовалось показать.

Заметим, что модель в случае выполнимости доказательства Гёделя всегда счетна. А значит, это доказательство теоремы о полноте дает также теорему Лёвегема — Скулема (см. ниже). Гёдель расширяет результат до счетного числа формул и до случая логики первого порядка с тождеством. Он также доказывает независимость аксиом.

В 1930 году Гёдель опубликовал статью, основанную на его диссертации (Gödel 1930), примечательную из-за включения теоремы о компактности, которая лишь вкратце изложена в диссертации. Гёдель формулирует теорему следующим образом: счетно бесконечное множество кванторных формул выполнимо тогда и только тогда, когда каждое конечное подмножество этих формул является выполнимым. Гёдель использует компактность для того, чтобы вывести обобщение теоремы о полноте.

Теорема о компактности была распространена на случай несчетных словарей Мальцевым в 1936 году (см. Mal’cev 1971), из чего сразу следует теорема Лёвенгейма — Скулема о повышении мощности. Теорема о компактности станет одним из основных инструментов в теории моделей, которая была тогда еще совсем молодой областью.

Важное следствие теоремы о полноте

Говорят, что теория категорична, если она имеет только одну модель с точностью до изоморфизма; она λ-категорична, если имеет только одну модель мощности λ с точностью до изоморфизма. Одно из главных следствий теоремы о полноте состоит в том, что категоричность терпит неудачу в случае арифметики Пеано и теории множеств Цермело–Френкеля.

Более конкретно, что касается аксиом Пеано первого порядка (далее PA), существование нестандартных моделей из них на самом деле следует из полноты вместе с компактностью. Эти модели, содержащие бесконечно большие целые числа, выстраиваются следующим образом: в язык арифметики добавляется символ новой константы c. PA расширяется до новой теории PA* посредством добавления бесконечной совокупности аксиом: {c > 0, c > 1, …}, где, например, 3 является S(S(S(0))). PA* конечно непротиворечиво (то есть каждое конечное подмножество PA* непротиворечиво), следовательно, оно непротиворечиво и поэтому по теореме о полноте имеет модель. 

Этот простой факт о моделях арифметики Пеано не был отмечен Гёделем ни в одной из публикаций, связанных с теоремой о полноте того времени, и, похоже, никто из общего сообщества логиков не обращал на него внимание еще очень долгое время. Конструкция Скулема с определимой ультрастепенью (см. Skolem 1933) дает прямое построение нестандартной модели истинной арифметики (которая расширяет арифметику Пеано, являющуюся множеством арифметических предложений, которые истинны для натуральных чисел). Но Скулем никогда не говорит о том, что существование подобных моделей следует из теорем о полноте и компактности. Гёдель в своем обзоре (Gödel 1934c) статьи Скулема также не упоминает этот факт, скорее отмечая, что невыполнение категоричности для арифметики вытекает из теоремы о неполноте. 

Что касается теории множеств, то невыполнение категоричности уже была замечено Скулемом в 1923 году, поскольку она вытекает из теоремы Лёвенгейма — Скулема: любая теория первого порядка в счетном языке, имеющая модель, имеет счетную модель. 

Наблюдение Скулема, в соответствии с которым категоричность не выполняется для теории множеств, потому что она имеет счетные модели, теперь известно как парадокс Скулема. Наблюдение четко акцентируется в статье Скулема, озаглавленной «Наблюдение об аксиоматических основах теории множеств». Как Скулем пишет в заключении, он не указывал относительность в теории множеств уже в 1915 году в силу того, что

В качестве отступления следует заметить, что в доказательстве теоремы Лёвенгейма — Скулема, в частности, той части теоремы, в которой выстраивается модель для выполнимого предложения, конструкция дерева Лёвенгейма и Скулема была более или менее такой же, как в диссертации Гёделя. В письме к Хао Вану от 1967 года Гёдель обращает внимание на то, что его доказательство полноты было почти получено Скулемом в 1923 году. Хотя Ван Хейенорт и Дребен отмечают, что «в течение большей части 1920-х годов основной проблемой при изучении теории квантификации была не семантическая полнота, но проблема разрешимости для квантификационной валидности, вытекающая из работ Шрёдера и Лёвенгейма» (Dreben and van Heijenoort 1986; примеры таких результатов будут включать разрешающую процедуру для исчисления одноместного предиката первого порядка по Бехману, Behmann 1922), по словам Гёделя, причины, по которым Скулем не получил полного доказательства, совершенно иные и весьма важны в философском плане, поскольку имеют отношение к тогдашнему широкому предубеждению против семантики и нефинитных методов:

Теорема о полноте в математическом отношении действительно является почти тривиальным следствием Skolem 1923. Однако факт заключается в том, что в то время никто (в том числе сам Скулем) не сделал такой вывод ни из Skolem 1923, ни из своих аналогичных соображений, как поступил я… Подобная слепота (или предрассудок, или как ее не назови) логиков в самом деле удивительна. Но я думаю, что объяснение лежит на поверхности. Оно кроется в широко распространенной нехватке верной эпистемологической установки по отношению к метаматематике и к нефинитным рассуждениям. (Gödel 2003)

Вопрос вклада Скулема в теорему о полноте широко обсуждался в van Atten and Kennedy 2009, а также в van Atten 2005.

Теоремы о неполноте

Гёдель упомянул о возможной неразрешимости вопроса о вещественных числах уже в своей диссертации 1929 года, выступая против формалистского принципа Гильберта, согласно которому непротиворечивость служит критерием существования. Фактически предоставление финитного доказательства непротиворечивости анализа выступало ключевой целью того, что тогда называлось программой Гильберта, наряду с доказательством его полноты. Соответственно, к этим вопросам обратился Гёдель, особенно к первому, который привел его к двум теоремам о неполноте. (Для обсуждения программы Гильберта см. стандартные ссылки: Sieg 1990, 1988, 1999; Mancosu 1998; Tait 1981, 2002; а также статью «Программа Гильберта».)

Первая теорема о неполноте дает контрпример к полноте, представляя арифметическое утверждение, которое не доказуемо и не опровержимо в арифметике Пеано, хотя и истинно в стандартной модели. Вторая теорема о неполноте показывает, что непротиворечивость арифметики не может быть доказана в рамках самой арифметики. Таким образом, теоремы Гёделя продемонстрировали неосуществимость программы Гильберта, если она характеризуется этими конкретными нерешенными задачами, связанными с непротиворечивостью и полнотой.

Следует отметить, что фон Нейман понимал обе теоремы именно в таком ключе даже до того, как к этому пришел Гёдель. На самом деле фон Нейман пошел гораздо дальше, взглянув на то, что они в совокупности показали неосуществимость классической математики. Как он писал Карнапу в июне 1931 года:

Таким образом, сегодня я придерживаюсь мнения, что, во-первых, Гёдель показал нереализуемость программы Гильберта. Во-вторых, больше нет оснований отвергать интуиционизм (если не учитывать эстетическую проблему, которая на практике также будет для меня решающим фактором). Поэтому я считаю, что состояние дискуссии об основаниях в Кёнигсберге устарело, поскольку фундаментальные открытия Гёделя выдвинули вопрос на совершенно другой уровень. 

И предыдущей осенью фон Нейман обратился к Гёделю с еще более жесткими словами:

Таким образом, я полагаю, что ваш результат решил вопрос оснований отрицательно: согласно ему строгого обоснования классической математики не существует. (Gödel 2003: 339). 

Самому Гёделю понадобилось несколько лет, чтобы увидеть, что эти аспекты программы Гильберта были решительно опровергнуты его результатами (Mancosu 2004).

Первая теорема о неполноте

В своем «Логическом путешествии» (Logical Journey, Wang 1996) Хао Ван опубликовал полный текст материала, который Гёдель написал (по просьбе Вана) на тему своего открытия теорем о неполноте. Этот материал лег в основу работы Вана «Некоторые факты о Курте Гёделе» и был прочитан и одобрен Гёделем:

Летом 1930 года я начал изучать проблему непротиворечивости классического анализа. Не вполне понятно, почему Гильберт хотел напрямую доказать непротиворечивость анализа финитными методами. Я отчетливо видел две отдельные проблемы: доказать непротиворечивость теории чисел с помощью финитной теории чисел и доказать непротиворечивость анализа по теории чисел. <…> Поскольку область финитной теории чисел не была четко определена, я начал с решения второй проблемы. <…> Я представлял вещественные числа предикатами в теории чисел… и обнаружил, что должен был использовать понятие истины (в теории чисел) для проверки аксиом анализа. Перечислением символов, предложений и доказательств в рамках данной системы я быстро обнаружил, что в арифметике понятие арифметической истины определить нельзя. Если бы можно было определить истину в самой системе, у нас вышло бы нечто наподобие парадокса лжеца, показывающего противоречивость системы… Обратите внимание, что данный аргумент можно формализовать, чтобы показать существование неразрешимых пропозиций, не приводя каких-либо отдельных примеров. (Если бы не было неразрешимых пропозиций, все (и только) истинные пропозиции были бы доказуемы в системе. Но тогда мы бы пришли к противоречию.) <…> В отличие от истины, доказуемость в данной формальной системе является эксплицитным комбинаторным свойством некоторых предложений системы, которое формально определяется подходящими элементарными средствами…

Мы видим, что Гёдель сначала попытался редуцировать проблему непротиворечивости анализа к аналогичной проблеме, связанной с арифметикой. Для этого ему потребовалось определение истины для арифметики, что в свою очередь привело к парадоксам, таким как парадокс лжеца («Это предложение ложно») и парадокс Берри («Наименьшее число, не определенное выражением, состоящим всего из четырнадцати английских слов»). Гёдель заметил, что такие парадоксы необязательно возникнут, если истина будет заменена доказуемостью. Но это означает, что арифметическая истина и арифметическая доказуемость не равнообъемны — из чего вытекает первая теорема о неполноте.

Приведенное описание открытия Гёделя было передано Хао Вану существенно позже свершения самого открытия; но в переписке Гёделя с Бернайсом и Цермело дается идентичное описание его пути к теоремам. (См. Gödel 2003a и 2003b соответственно.) Из этих данных мы видим, что неопределимость истины в арифметике, результат, приписываемый Тарскому, по всей вероятности, был получен в той или иной форме Гёделем еще в 1931 году. Но он не публиковал результат; предвзятость мнений логиков в то время в отношении понятия истины, уверенно вышедшая на первый план (когда Тарский в 1935 году объявил о своих результатах в отношении неопределимости истины в формальных системах), возможно, послужила сдерживающим фактором для публикации Гёделем своей теоремы.

Доказательство первой теоремы о неполноте

Теперь мы рассмотрим доказательство двух теорем, которое формулирует результаты Гёделя в арифметике Пеано. Сам Гёдель использовал систему, связанную с той, что была определена в «Основаниях математики» (Principia Mathematica) Рассела и Уайтхеда, но содержащую арифметику Пеано. В нашем изложении первой и второй теорем о неполноте мы обозначим ссылки на арифметику Пеано как на Р, следуя обозначениям Гёделя.

Прежде чем перейти к деталям формального доказательства, определим понятие ω-непротиворечивости, используемое Гёделем в первой теореме о неполноте: P ω-непротиворечива, если P ⊢ ¬φ(n) для всех n влечет P ⊬ ∃xφ(x). Естественным образом из понятия следует непротиворечивость; само же оно вытекает из предположения, что натуральные числа удовлетворяют аксиомам арифметики Пеано.

Одним из основных технических инструментов, используемых в доказательстве, служит нумерация Гёделя, механизм, который присваивает натуральные числа термам и формулам нашей формальной теории Р. Существуют разные способы сделать это. Наиболее распространенным является единственное представление натуральных чисел как произведений степеней простых чисел. Каждому символу s теории чисел присваивается положительное натуральное число #(s) фиксированным, но произвольным образом, например:

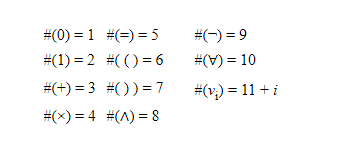
Натуральное число, соответствующее последовательности w = < w0,…, wk > символов, равно

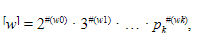
где pk является k+1-м простым числом. Оно называется гёделевым номером и обозначается ⌈w⌉. Таким образом, мы можем присвоить гёделевы номера формулам, последовательностям формул (как только нами принимается метод, позволяющий установить, когда заканчивается одна формула и начинается другая) и, самое главное, доказательствам.

Существенный момент: когда формулу интерпретируют в качестве натурального числа, то цифра, соответствующая этому числу, может рассматриваться как аргумент формулы, что позволяет синтаксису, так сказать, «ссылаться» на себя (т.е. когда нумерал подставляется в формулу с гёделев номером, который представляет нумерал). В конечном итоге это позволит Гёделю формализовать парадокс лжеца (с «доказуемостью» вместо «истины»), подставив в формулу «формула, код которой х, недоказуема» ее собственный код натурального числа (или, точнее, соответствующий нумерал).

Еще одним понятием, требуемым для формализации, является нумерическая выразимость теоретико-числовых предикатов. Теоретико-числовая формула φ(n1, …, nk) нумерически выразима в P, если для каждого кортежа натуральных чисел (n1,…,nk):

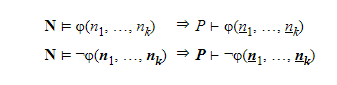
где n — формальный терм, обозначающий натуральное n. (В P это S(S(… S(0)…), где n — число итераций функции следования, применяемых к символу постоянной 0.) Одной из основных целей выступает нумерическое выражение предиката

Prf(x, y): «последовательность с гёделевым номером x служит доказательством предложения с гёделевым номером y». 

Достижение этой цели включает в себя определение сорока пяти отношений, каждое из которых определяется предыдущими. Все они примитивно-рекурсивны. Необходимыми отношениями являются, среди прочего, те, которые для данного натурального числа утверждают, что оно кодирует последовательность, формулу или аксиому, или что это код, обозначаемый Sb(ru1…unZ(x1)…Z(xn)), формулы, полученной из формулы с кодом r подстановкой xi-го нумерала для i = 1, …, n вместо свободной переменной ui. Сорок пятое примитивно-рекурсивное отношение определяется как Prf(x, y), а сорок шестое — 

Prov(y): «предложение с гёделевым номером y доказуемо в P»,

которое, не будучи примитивно-рекурсивным, получается из Prf(x, y) путем экзистенциальной квантификации x. (Prov(y) удовлетворяет только «положительной» части нумерической выразимости, а не отрицательной; однако отрицательная часть не требуется.)

В теореме V своей статьи Гёдель доказывает, что любой теоретико-числовой предикат, являющийся примитивно-рекурсивным, нумерически выразим в Р. Таким образом, поскольку Prf(x, y) и подстановка примитивно-рекурсивны, они разрешаются P, когда замкнутые термы заменяются свободными переменным x и y. Как мы увидим, здесь и заключается вся суть дела. Другим ключевым моментом для нумерической выразимости является то, что, хотя мы неформально интерпретируем, например, Prov(Sb(ru1…unZ(x1)…Z(xn))), следующим образом: «формула с гёделевым номером r доказуема при подстановке гёделевого номера для xi-го числа вместо i-й переменной», — ни формальное утверждение в теории P, ни все, что мы доказываем по поводу нее, не отсылает к таким значениям. Напротив, Prov(Sb(ru1…unZ(x1)…Z(xn))), представляет собой бессмысленную цепочку логических и арифметических символов. Как указывает Гёдель в введении к своей теореме V: «Тот факт, что можно неопределенно сформулировать утверждение, что каждое рекурсивное отношение определимо в системе P (если формулам системы придается обычное значение) и выражается в точном языке, без каких-либо ссылок на любую интерпретацию формул Р, согласно следующей теореме (V)» (Gödel 1986: 171, курсив Гёделя).

Гёдель в теоремах о неполноте использует метод, примененный в теореме Гёделя о неподвижной точке, как она называется в наши дни. Хотя Гёдель и конструирует неподвижную точку в ходе доказательства теоремы о неполноте, он не формулирует теорему о неподвижной точке эксплицитно. Теорема о неподвижной точке гласит:

Теорема 2 (теорема Гёделя о неподвижной точке)

Если φ(v0) — формула теории чисел, то существует такое предложение ψ, что P ⊢ ψ ↔ φ(⌈ψ⌉), где ⌈ψ⌉ — формальный терм, соответствующий натуральному числовому коду ⌈ψ⌉. 

Доказательство. Пусть σ(x,y,z) — формула, которая нумерически выражает теоретико-числовой предикат «y — это гёделев номер формулы, полученной путем замены переменной v0 в формуле, чей гёделев номер x, на терм z». Пусть θ(v0) будет формулой ∃v1(φ(v1) ∧ σ(v0,v1,v0)). Пусть k = ⌈θ(v0)⌉ и ψ = θ(k). Теперь можно непосредственно построить P ⊢ ψ ↔ φ (⌈ψ⌉). 

Предложение теории опровержимо, если его отрицание доказуемо. Первая теорема о неполноте в формулировке Гёделя гласит:

Теорема 3 (первая теорема Гёделя о неполноте) 

Если P ω-непротиворечива, то существует предложение, которое недоказуемо и неопровержимо в рамках P.

Доказательство. Путем осмотрительного кодирования синтаксиса, упомянутым выше, запишем формулу Prf(x, y) теории чисел, представимую в P, так что

n кодирует доказательство φ ⇒ P ⊢ Prf(n, ⌈φ⌉). 

и

n не кодирует доказательство φ ⇒ P ⊢ ¬Prf(n, ⌈φ⌉). 

Обозначим через Prov(y) формулу ∃x Prf(x,y). Согласно теореме 2, есть предложение φ со свойством

P ⊢ (φ ↔ ¬Prov(⌈φ⌉)). 

Таким образом φ сообщает «я недоказуемо». Заметим теперь, что если P ⊢ φ, то в силу (1) найдется n такое, что P ⊢ Prf(n, ⌈φ⌉), следовательно, P ⊢ Prov(⌈φ⌉), а значит, в силу (3) P ⊢ ¬φ , поэтому P противоречива. Таким образом 

P ⊬ φ 

Кроме того, в силу (4) и (2) имеем P ⊢ ¬Prf(n, ⌈φ⌉) для всех натуральных чисел n. По ω-непротиворечивости, P ⊬ ∃x Prf(x, ⌈φ⌉). Таким образом, (3) дает P ⊬ ¬φ. Мы показали, что если P ω-непротиворечива, то φ независима от P.

Завершая доказательство первой теоремы, Гёдель замечает: «…легко заметить, что приведенное только что доказательство конструктивно; а именно… метод доказательства интуиционистски неоспорим…» (Gödel 1986: 177). Это связано с тем, что, как он указывает, все экзистенциальные утверждения основаны на его теореме V (обеспечивающей нумерическую выразимость примитивно-рекурсивных отношений), которая интуиционистски неоспорима.

Вторая теорема о неполноте

Вторая теорема о неполноте устанавливает недоказуемость в теории чисел непротиворечивости теории чисел. Сначала мы должны записать теоретико-числовую формулу, которая выражает непротиворечивость аксиом. Это удивительно просто. Допустим, что Con(P) — предложение ¬Prov(⌈0 = 1⌉). 

Теорема 4 (вторая теорема Гёделя о неполноте)

Если P непротиворечива, то Con(P) недоказуемо в рамках P.

Доказательство. Пусть φ будет как в (3). Рассуждение, используемое для вывода «если P ⊢ φ, то P ⊢ 0 ≠ 1», не выходит за рамки теории элементарных чисел, и поэтому, хотя и с большими усилиями (см. ниже), формализуется в P. Это дает: P ⊢ (Prov(⌈φ⌉) → ¬Con(P)), и таким образом, по (3), P ⊢ (Con(P) → φ). Поскольку P ⊬ φ, мы должны получить P ⊬ Con(P).

Вышеприведенное доказательство (в схематическом виде) второй теоремы о неполноте обманчиво просто, поскольку оно избегает формализации. Строгое доказательство должно было бы установить доказательство «если P ⊢ φ, то P ⊢ 0 ≠ 1» в P.

Стоит отметить, что при доказательстве второй теоремы Гёделя о неполноте ω-непротиворечивость не нужна. Отметим, что ¬Con(P) также недоказуемо в силу непротиворечивости P и того факта, теперь известного как теорема Лёба, что P ⊢ Prov(⌈φ⌉) влечет P ⊢ φ.

Допущение ω-непротиворечивости в первой теореме о неполноте было устранено Россером в 1936 году и заменено более слабым понятием непротиворечивости. Обобщение Россера включает применение теоремы о неподвижной точке к формуле R(x): «для всех z: либо z не является гёделевым номером доказательства формулы с гёделевым номером x, либо существует доказательство короче, чем z, отрицания (формулы с гёделевым номером) x» (см. Rosser 1936).

Что касается второй теоремы о неполноте, то, как мы видели, аргументация частично основана на формализации доказательства первой теоремы о неполноте. Этот шаг опущен в публикации Gödel 1931. Гёдель планировал включить его во вторую часть. Но вместо того, чтобы ее написать, он обратился к проблеме континуума. (В части II должны были быть также проработаны и другие вопросы: «истинная причина неполноты» и применимость двух теорем к другим системам.) Возможно, он не желал предпринимать то, что выглядело как упражнение в формализации, полагаясь вместо этого для убедительности на неформальные доводы (в чем он преуспел). Однако данный шаг оказался несколько нетривиальным. Как пишет Клини в своем введении к Gödel 1931 о неформальном изложении: «Конечно, идея аргумента для теоремы XI (о непротиворечивости) была очень убедительной; но оказалось, что проработка подробностей потребовала несколько больших трудов и забот, чем ожидалось». (См. Gödel 1986: 126–141.) В итоге полное доказательство второй теоремы было дано Гильбертом и Бернайсом (Гильберт, Бернайс 1982). Более компактное рассмотрение теоремы представил Лёб в Löb 1956, а затем Феферман в работе «Арифметизация метаматематики в общей постановке» (Feferman 1960/1961) выдвинул краткий и полностью обобщенный подход как к первой, так и к второй теоремам. 

Более подробное обсуждение этой проблемы можно найти в статье о теоремах Гёделя о неполноте.

Теоремы об ускорении

В теореме Гёделя об ускорении, опубликованной в реферате «О длине доказательств» (Gödel 1936), говорится, что хотя некоторые предложения арифметики истинны, но недоказуемы, существуют другие предложения, которые доказуемы, но даже кратчайшее доказательство длиннее, чем любая граница, заданная заранее как рекурсивная функция предложения. Более точно:

Теорема 5. 

Для любой рекурсивной функции f существуют доказуемые предложения φ арифметики такие, что кратчайшее доказательство превышает f(⌈φ⌉) по длине. 

Доказательство, которое мы опишем, чувствительно к конкретному понятию, которое мы используем для установления длины доказательства. Другая возможность, которую и имеет в виду Гёдель, — это количество формул в доказательстве. Басс (см. ниже) доказывает теорему для обоих случаев, поэтому оба разрешены.

Доказательство. Пусть f — общерекурсивная функция. По теореме Гёделя о неподвижной точке, существует формула φ(n), утверждающая, что «φ(n) не имеет доказательств в PA короче, чем f(n)». Это допустимо, если длина измеряется числом символов, так как нам нужно искать только конечное число доказательств короче f(n). Заметим, что φ(n) истинно для всех n, так как если φ(n) были ложными, то было бы короткое доказательство φ(n), и потому, по состоятельности, φ(n) было бы истинным, что является противоречием: φ(n) будет истинным и ложным. Это можно формализовать в PA, следовательно, мы получаем результат, согласно которому для каждого n предложение φ(n) доказуемо в PA. Так как φ(n) истинно для всех n, оно не может иметь доказательства в PA, которое было бы короче f(n). 

Теорема об ускорении является результатом рассмотрения и разработки доказательства теоремы о неполноте. Она применяет метод неподвижной точки к понятию недоказуемости коротким доказательством, а не к простой недоказуемости, как в исходной идее. Доказательство выстраивается в том же ключе, что и доказательство теоремы о неполноте. Интересно, что оно датируется тем же годом, что и построение Россера, которое исключает использование ω-непротиворечивости в первой теореме о неполноте; как и теорема Гёделя об ускорении, построение Россера обращается к вопросу коротких и длинных доказательств. Гёдель никогда не отдавал доказательство теоремы об ускорении на публикацию. На протяжении нескольких лет было обнародовано несколько связанных с ним доказательств, однако первое полное доказательство изначального результата Гёделя было дано только в 1994 году Сэмом Бассом в его работе «О теоремах Гёделя о длинах доказательств I: Количество строк и ускорений для арифметики». (Buss 1994). Басс также дает второе доказательство теоремы, которое позволяет избежать самореференции, следуя технике Стейтмана. Гёдель измеряет длину доказательств числом формул; но есть и другие возможности, такие как количество символов в доказательстве. Случай теоремы об ускорении, где длина доказательства измеряется числом символов, был доказан Мостовским в 1952 году (Mostowski 1982). Доказательства схожих результатов см. в Ehrenfeucht and Mycieleski 1971 и Parikh 1971. Хотя оба способа служат одинаково естественными мерами длины доказательства, доказательство теоремы для длины, измеряемой числом символов, позволяет избежать технического усложнения, вносимого другой мерой: существует только конечное число доказательств с заданным количеством символов, в то время как число доказательств с заданным количеством формул бесконечно.

Гёдель сформулировал теорему об ускорении иначе, чем это сделали выше мы. Пусть Sn — система логики n-го порядка, причем переменные первого уровня рассматриваются как пробегающие натуральные числа. В этой настройке переменные второго уровня пробегают множества натуральных чисел и т.д. В формулировке Гёделя:

Теорема 6.

Пусть n — натуральное число > 0. Если f — вычислимая функция, то существует бесконечно много формул A, доказуемых в Sn, таких, что если k — длина кратчайшего доказательства A в Sn, а l — длина кратчайшего доказательства А в Sn+1, то k > f(l).

Схема доказательства. Идея заключается в следующем: пусть φ(x) — формула, как и выше, для которой φ(m) не имеет короткого доказательства в Sn для любого m. Предположим, что мы имеем систему более высокого типа Sn+1, в которой можем доказать ∀xφ(x). Это доказательство имеет постоянную длину. Таким образом, каждая φ(m) выводится из этого всеобщего утверждения одним применением логического правила ∀xφ(x) → φ (t). Следовательно, φ(m) имеет в данной системе для всех m краткое доказательство. 

Какова разновидность более строгой системы, в которой ∀xφ(x) доказуемо? Мы можем рассмотреть логику второго порядка, в которой определим предикат N(x) для множества натуральных чисел и, кроме того, доказуемо, что новый предикатный символ Tr(x) отвечает индуктивным частям определения истинности формул первого порядка арифметики, релятивизированных к N. Тогда более строгая система сможет доказать, что доказуемые первопорядковые предложения арифметики удовлетворяют предикату Tr. Согласно приведенному выше рассуждению, мы можем доказать в более строгой системе, что ∀xφ(x) удовлетворяет Tr. Затем, добавив нескольких строк, мы можем доказать, что каждая φ(n) отвечает Tr. Из-за природы φ(n) отсюда вытекает, что более строгая система имеет (короткое) доказательство φ(n). Альтернативной системой являются аксиомы Пеано (PA) в расширенном языке, где имеется новый предикатный символ Tr и аксиомы, в которых указано, что предикат Tr кодирует отношение удовлетворительности для всех предложений словаря, не содержащих Tr.

Труды Гёделя в области теории множеств

Непротиворечивость гипотезы о континууме и аксиомы выбора

Гёделевское доказательство согласованности континуум-гипотезы с аксиомами теории множеств Цермело-Френкеля является шедевром и, возможно, величайшим достижением его математической жизни. Это связано с тем, что помимо арифметизации практически все технические средства, используемые в доказательстве, должны были быть изобретены с нуля.

Континуум-гипотеза (далее CH) была сформулирована Георгом Кантором и была первой в списке из двадцати трех нерешенных проблем Гильберта, приведенных в его знаменитом обращении к Международному математическому конгрессу в Париже в 1900 году. Проблема изложена Гильбертом следующим образом. Пусть А — бесконечное множество вещественных чисел. Тогда A либо счетно, либо имеет мощность 2ℵ0, то есть A находится во взаимно однозначном соответствии либо с набором натуральных чисел, либо с множеством всех вещественных чисел (иначе именуемым континуумом). Другой способ сформулировать CH состоит в том, что (первое несчетно бесконечное кардинальное число) ℵ1 = 2ℵ0.

Еще в 1922 году Скулем предположил, что CH не зависит от аксиом теории множеств, предложенных Цермело в 1908-м. Тем не менее в 1926-м Гильберт опубликовал (ложное) доказательство. В 1937 году Гёдель доказал, что CH не входит в противоречие с аксиомами теории множеств ZF. (В дальнейшем мы используем стандартные сокращения для теории множеств Цермело-Френкеля, ZF, и Цермело-Френкеля с аксиомой выбора, ZFC.) Непротиворечивость отрицания CH была показана Полом Коэном в 1961 году (см. Cohen 1963), и вместе с результатом Гёделя отсюда можно сделать вывод, что CH не зависит от ZF (и ZFC).

Коэн изобрел важную новую технику, называемую форсингом, в процессе доказательства своего результата; этот метод в настоящее время является основным методом, используемым для построения моделей теории множеств. Форсинг привел к возрождению интереса к формализму среди специалистов, занимающихся теорией множеств, и разнообразие моделей стало признаком «сущностной вариативности теории множеств» (Dehornoy 2004). Также форсинг искоренил представление о том, что существует предполагаемая модель теории множеств — точку зрения, которую Гёдель отстаивал по крайней мере с 1947 года, если не раньше. В последнее время появились признаки того, что CH может вновь рассматриваться как проблема, которую следует решить математически (с помощью, конечно, новых очевидных аксиом, расширяющих ZF). (См., напр., Woodin 2001 и Foreman 1998). Если какое-либо из предложенных решений получит признание, это подтвердит мнение Гёделя о том, что CH в конечном итоге будет решена путем нахождения явного расширения аксиом ZF для теории множеств. Программа, связанная с этим представлением, называется гёделевой программой больших кардинальных чисел.

Гёделевское доказательство согласованности континуум-гипотезы и аксиомы выбора с аксиомами теории множеств Цермело–Френкеля

Проблема континуума решается путем нахождения перечисления вещественных чисел, которое индексируется счетными порядковыми числами, — стратегия, которая уже была признана Гильбертом как многообещающая. Трудная задача (и интуиция) доказательства состоит в том, чтобы построить «малую» модель, в которой допускается абсолютное минимальное количество вещественных чисел и которая при этом была бы достаточно велика, чтобы быть закрытой относительно всех операций, чье существование утверждается аксиомами ZF.

Идея Гёделя является доказательством относительной непротиворечивости, полученным путем построения так называемой «внутренней модели» для ZF совместно с CH. Внутренняя модель представляет собой подмножество M набора V всех множеств (см. ниже), которое удовлетворяет аксиомам ZF, когда рассматриваются только множества в M. Внутренняя модель Гёделя называется внутренней моделью конструируемых множеств (см. ниже), и обозначается L. Все, что истинно во внутренней модели, не противоречит ZF по той же причине, по которой непротиворечива любая теория с моделью. Артефактом построения выступает то, что аксиома выбора (здесь и далее AC) выполняется во внутренней модели Гёделя, и, следовательно, Гёделем была установлена согласованность АС с ZF. Позднее Серпинский показал, что AC на самом деле является следствием обобщенной континуум-гипотезы (или GCH), которая гласит, что для каждого κ, 2κ = κ+ (см. Sierpinski 1947).

Гёдель опубликовал две версии этих теорем в 1939 и 1940 годах, озаглавленные «Доказательство непротиворечивости обобщенной континуум-гипотезы » и «Согласованность аксиомы выбора и обобщенной континуум-гипотезы с аксиомами теории множеств» соответственно. Хотя в версии 1939 года совершенно определенно отсутствует множество подробностей — прежде всего аргументы, показывающие, что если L построена внутри самой L, то получается та же самая L; то есть так называемые аргументы абсолютности отсутствуют. Также отсутствуют подробности доказательств того, что аксиомы ZF имеют место в L. Однако, в отличие от второй теоремы о неполноте, Гёдель впоследствии дал полное подробное доказательство двух вышеуказанных теорем в монографии 1940 года. (Доказательство 1940 года существенно отличается от первой версии. Подробнее о двух доказательствах и различии между ними см. в Solovay 1990 и Kanamori 2006.)

Изобразим теперь схему доказательства согласованности CH и AC с ZFC с использованием современной терминологии. Некоторые предварительные понятия: сначала мы задаем стратифицированный теоретико-множественный универсум, обозначаемый V. (V также известен как кумулятивная иерархия). Его можно получить путем итерирования операции показательного множества (℘), начиная с пустого множества:

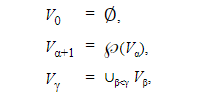
где α, β — любые порядковые числа, γ — предельное порядковое число, а ℘(x) обозначает показательное множество x. Наконец

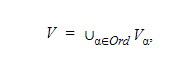
где Ord обозначает класс всех порядковых чисел. 

Конструируемая иерархия L схожим образом определяется рекурсией по порядковым числам. Но в то время как операция показательного множества повторяется для получения кумулятивной иерархии, уровни конструируемой иерархии определяются строго предикативно, то есть путем включения на следующем уровне только тех множеств, которые первопорядково определимы с использованием параметров предыдущего уровня. Точнее, пусть Def(A) обозначает множество всех подмножеств A, определимых в структуре <A,∈> формулами первого порядка с параметрами в A. (Дальнейшие сведения об определимости см. в статье о теории моделей в настоящей энциклопедии.) 

С помощью этих обозначений конструктивная иерархия определяется индукцией над порядковыми числами следующим образом:

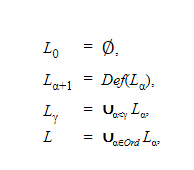
Множество x называется конструируемым, если x ∈ L. Аксиома, утверждающая, что все множества конструируемы, обозначается V = L и называется аксиомой конструируемости. Заметим, что L — собственный класс, а не множество; хотя, как мы увидим, каждая Lα является множеством, а предикат «x конструируемо» на самом деле представляет собой определимый терм языка. 

Дальнейшая наша задача состоит в том, чтобы показать, что L служит моделью ZF. Множество или класс транзитивны, если их элементы также являются подмножествами. С помощью тщательной трансфинитной индукции можно продемонстрировать, что Lα транзитивна для каждого α; а потому и сама L транзитивна. Этот факт наряду с замечанием, что некоторые элементарные свойства замыкания имеют место в L, достаточны, чтобы показать, что L выступает моделью ZF. (Действительно, как оказывается, L служит минимальной транзитивной моделью аксиом ZF, содержащей все порядковые числа, а значит, в этом смысле она канонична.)

Более конкретно, доказательство того, что аксиомы ZF за исключением аксиомы выделения истинны в L, сводится к тому, что, упрощенно говоря, любое множество со свойством P, чье существование утверждает аксиома ZF, можно обнаружить в L, если учитывать релятивизацию PL свойства P к L. (Свойство P релятивируется к внутренней модели M заменой каждого квантора ∃xφ на ∃x(x ∈ M ∧ φ) и каждого квантора ∀xφ на ∀x(x ∈ M → φ).) Что касается аксиомы выделения, то для ее проверки необходимо показать, что множество, чье существование утверждается, построено на некотором уровне следования Lα + 1. Чтобы это доказать, требуется важный принцип теории множеств, который на современном техническом жаргоне называется принципом отражения Леви (или принципом отражения ZF). Этот принцип гласит, что любое утверждение в языке ZF, которое истинно в V, уже истинно на каком-то уровне любой непрерывно растущей иерархии, такой как L. (Историю принципа см. в Kanamori 2006.) Принцип отражения Леви дает уровень α, на котором построены все элементы множества. Гёдель фактически не использовал принцип отражения Леви, но использовал аргумент, лежащий в основе доказательства принципа Леви.

Как только установлено, что L является моделью ZF, становится возможным доказать, что и CH, и AC имеют место в L. С этой целью сначала должно быть показано, что определение L является абсолютным для L. Абсолютность определяется следующим образом: при данном классе M предикат P(x) называется абсолютным для M, если и только если для всех x ∈ M, P(x) ↔ PM(x).

Доказательство абсолютности предиката «x конструируемо» требует формализации понятия «определимость», что в свою очередь требует формализации понятия «выполнимость». Это связано с тем, что предикат «x конструируемо» говорит о множестве, в котором для некоторого порядкового числа α и для некоторой формулы φ с параметрами в Lα верно, что x = {y ∈ Lα | Lα ⊨ φ(y)}. Данная часть доказательства утомительна, но беспроблемна. 

Как только абсолютность L установлена, отсюда следует, что ZF удовлетворяет аксиоме конструируемости, если релятивизирована к L; то есть ZF ⊢ (V=L)L. В частности, аксиома V=L непротиворечива, если ZF непротиворечива.

Приведем теперь идею доказательства CH и AC в ZF + V = L. (Подробное изложение доказательства можно найти в стандартных источниках. См., напр., главу Девлина о конструируемости в Barwise 1977; см. также Kunen 1983 и Jech 2003.)

Что касается CH, то идея доказательства ее наличия в L состоит в следующем: Гёдель показал, что в предположении V = L каждое вещественное число встречается на некотором счетном уровне L-иерархии. Так как каждый счетный уровень сам является счетным (в конце концов, существует только счетное число возможных определяющих формул) и существуют счетные уровни ω1, то должны быть только вещественные числа ω1.

Трудность данного пункта, если не всего доказательства в целом, заключается в том, чтобы показать, что каждое вещественное число уже построено на счетном уровне L-иерархии. С этой целью Гёдель утверждал: пусть А — вещественное число, рассматриваемое как множество натуральных чисел. По принципу отражения Леви и теореме Лёвенгейма — Скулема, существует счетная подмодель < M, ∈ > из < L, ∈ >, удовлетворяющая достаточно большой конечной части аксиом ZF + V = L, так что A принадлежит M. Посредством простой процедуры < M, ∈ > можно преобразовать в транзитивную модель < N, ∈ >. Эта процедура, использованная Гёделем уже в 1937 году, была эксплицитно выделена Мостовским (Mostowski 1949). Полученная модель называется теоремой Мостовского о транзитивном коллапсе.

Обсудим эту важную методику. Предположим, что < M, E > —хорошо обоснованная модель аксиомы экстенсиональности. Вследствие хорошей обоснованности двуместного предиката E на M и принципа трансфинитной рекурсии уравнение π(x) = {π(y) | y ∈ M ∧ yEx} определяет единственную функцию на M. Область значений N оператора π транзитивна, поскольку если π(a) ∈ N и y ∈ π(a), то y = π(b) для некоторого b ∈ M с bEa, откуда π(b) ∈ N. То, что π представляет собой изоморфизм между < M, E > и < N, ∈>, можно доказать с помощью трансфинитной индукции на элементах на M, вновь опирающейся на обоснованность E. Обоснованность < M, E > на практике зачастую вытекает из того, что < M, E > служит подмоделью некоторого < Vα, ε >.

Вернемся теперь к доказательству CH в L. Для построения транзитивного множества N мы использовали теорему Мостовского о транзитивном коллапсе. Как оказалось, вещественное число A все еще остается элементом из < N, ∈>. По основным свойствам L, < N, ∈> должно быть < Lα , ∈ > для некоторого α. Поскольку N счетно, α также счетно. (Можно показать, что |Lα| = |α| + ℵ0.) Таким образом, A конструируемо на счетном уровне, что и требовалось показать.

Что касается AC, то Гёдель демонстрирует определимое вполне упорядочение, то есть формулу теории множеств, которая определяет в L вполне упорядочение всех L. Формула сложна для записи, но идея проста. Множество x предшествует множеству y в упорядочении, если и только если x встречается в L-иерархии на более раннем уровне Lα , чем y, либо они встречаются на одном уровне, но x определяется более короткой формулой, чем y, либо они определяются по одной и той же формуле, но параметры в определении x встречаются в L раньше, чем параметры y. Это вполне упорядочение L показывает, что AC имеет место в L.

Тем самым завершается доказательство непротиворечивости AC и CH в L.

Отметим, что Гёдель в Gödel 1939 и 1940 доказал больше того, что показано здесь, а именно обобщенную континуум-гипотезу в L и, следовательно, ее согласованность с ZF.

Следствия непротиворечивости

Как отмечалось выше, уже в 1920-х годах было высказано предположение, что CH может быть независима от ZF или ZFC. Вначале допустив, что аксиома конструируемости может быть «абсолютно непротиворечивой», то есть не фальсифицируемой никаким дальнейшим расширением модели ZF + V = L, в работе 1947 года «Что такое континуум-гипотеза Кантора?», Гёдель впоследствии предположил, что CH окажется независимой. Таким образом, главным следствием результата Гёделя в том, что касается вопроса о доказательстве независимости CH, было указание математикам на необходимость добавления неконструируемых множеств к модели теории множеств с целью установления непротиворечивости отрицания CH. В 1961 году Дана Скотт доказал, что отказ от аксиомы конструируемости следует из существования измеримого кардинального числа, что противоречит гипотезе, предложенной Гёделем в 1940 году (Cм. Scott 1961. Кардинальное число κ считается измеримым, если существует неглавный κ-полный ультрафильтр в показательной булевой алгебре κ). В 1963 году, как отмечалось, Пол Коэн доказал непротиворечивость отрицания CH путем добавления неконструируемых множеств к внутренней модели.

Какие другие открытые вопросы теории множеств могут быть решены методом Гёделя? Сам Гёдель отметил некоторые последствия. Они связаны с так называемыми проективными множествами вещественных чисел и конечными последовательностями вещественных чисел. Простейшими проективными множествами являются замкнутые множества, также называемые Π10-множествами. Множество Σ1n+1, если оно является проекцией Π1n-подмножества вещественной плоскости. Множество Δ1n+1, если оно и его дополнение являются Σ1n+1. Гёдель заметил, что существует как измеримое нелебеговское множество Δ12, так и несчетное Π11-множество без совершенного подмножества в L. (Множество вещественных чисел совершенно, если оно замкнуто, непусто и не имеет изолированных точек. Такие множества имеют мощность континуума.) Гёдель дал схему доказательства в 1951 году во втором издании Gödel 1940. 

Впоследствии выяснилось, что аксиома V = L дает практически полное расширение ZFC. Это означает, что помимо предложений, вытекающих из теорем о неполноте Гёделя, по существу все теоретико-множественные вопросы могут быть решены с помощью аксиом V = L. Отсюда не следует, что результаты тривиальны в каком бы то ни было смысле. Действительно, оказалось, что L — довольно сложная структура, несмотря на ее относительно простое описание. Что касается решения открытых теоретико-множественных вопросов в L, значительным событием стало появление теории Дженсена о тонкой структуре L (Jensen 1972). Если вспомнить, что шаг следования Lα +1 в определении конструируемой иерархии добавляет к L все подмножества Lα , определимые формулами первого порядка φ над (Lα, ∈), теория тонкой структуры, грубо говоря, разветвляет шаг от Lα to Lα+1 на более мелкие этапы в соответствии со сложностью определяющей формулы φ. Дженсен посредством тонкой структуры ввел понятие усиления CH, обозначенное ◊, которое он применил для построения дерева Суслина в L, и комбинаторный принцип □, который он использовал, чтобы показать, что гипотеза Суслина не противоречит CH.

Взгляд Гёделя на аксиому конструируемости

Если бы он не думал таким образом с самого начала, Гёдель вскоре пришел бы к выводу о том, что аксиома конструируемости была неправдоподобной. Как он заметил в конце своей статьи 1947 года «Что такое континуум-гипотеза Кантора?»:

…очень подозрительно, что в отличие от многочисленных правдоподобных пропозиций, влекущих отрицание гипотезы о континууме, не известно ни одного правдоподобной пропозиции, которая бы влекла континуум-гипотезу. (Gödel 1990: 186)

Гёдель был склонен рассматривать L в подобном ключе из-за лейбницианского представления о том, что вместо того, чтобы считать универсум достаточно «малым», то есть содержащим минимальное число множеств, более естественно было бы думать о том, что теоретико-множественный универсум столь велик, сколь возможно. Это воззрение отражалось в его интересе к принципам максимизации, то есть к принципам, которые ориентированы на поддержку интуитивной идеи о том, что теоретико-множественный универсум максимален в том смысле, что в него ничто не может быть добавлено; а также в убеждении Гёделя, что принципы максимизации в конечном итоге урегулируют такие положения, как CH. Как высказался Гёдель в письме к Уламу в конце 1950-х годов о принципе максимальности фон Неймана:

Большой интерес к этой аксиоме заключается в том, что она выступает принципом максимальности, в чем-то схожим с аксиомой Гильберта о полноте в геометрии. Ибо, грубо говоря, в ней говорится, что любое множество, которое не влечет противоречивость каким-либо конкретным определенным образом, существует. Ее совпадение с принципом максимума также объясняет тот факт, что эта аксиома влечет аксиому выбора. Я считаю, что основные проблемы теории множеств, такие как проблема континуума Кантора, будут решены удовлетворительно только с помощью более сильных аксиом такого рода, которые в определенном смысле противоположны или дополнительны по отношению к конструктивистской интерпретации математики. (Ulam 1958, цит. по Gödel 1990: 168. Заметим, что эта цитата отличается от весьма похожего отрывка Gödel 2003: 295)

Двадцатью годами ранее, в 1938 году, Гёдель как будто бы иначе писал об аксиоме конструируемости:

Пропозиция A (т.е. V = L), добавленная как новая аксиома, как кажется, дает естественное завершение аксиом теории множеств, поскольку она задает расплывчатое понятие произвольного бесконечного множества определенным образом. (Gödel 1986: 27)

Возможно, под «естественным завершением» Гёдель здесь понимал «правильное завершение», а возможно, он лишь хотел сообщить, что аксиома конструируемости определенным образом задает понятие множества. В любом случае в 1972 году в дискуссиях с Ваном о конструируемости он использовал термин «естественный» в ином смысле:

Гёдель больше рассказывал о связи между аксиомами бесконечности и конструируемой вселенной… [он заметил, что] предварительные понятия, такие как конструируемые множества, необходимы для того, чтобы прийти к естественному понятию, например, к множеству. (Wang 1996: 144)

Это напоминает замечание Хью Вудина о том, что изучение форсинга приводит к лучшему пониманию V — общий принцип заключается в том, что изучение моделей теории полезно не только для понимания самой теории, но и для лучшего представления о V (Woodin, 1988).

Дальнейшие сведения о программе Гёделя и ее отношении к CH см., напр., в Steel, Feferman et al. 2000. О результатах Гёделя, их истории и значимости см. в Floyd/Kanamori 2006 и Kennedy 2006. 

Труды Гёделя в области интуиционистской логики и арифметики

Интерес Гёделя к интуиционизму был глубоким и длительным. Хотя сам он не разделял эту позицию, он внес ряд важных вкладов в интуиционистскую логику. Возможно, значимость, которую он придает понятию свидетельства (см. ниже), побудила его пристально рассмотреть данную область.

Обсудим достижения Гёделя в области интуиционистской логики в хронологическом порядке.

Интуиционистская пропозициональная логика не является конечнозначной

И многозначная логика, введенная Лукасевичем в 1920-е годы (Łukasiewicz 1970), и интуиционистская логика, формализованная Гейтингом в 1930 году, не удовлетворяют закону исключенного среднего. Поэтому вполне естественно было задаться вопросом, можно ли представить интуиционистскую логику в качестве многозначной, и действительно, многие логики в 1920-х годах предполагали именно это. В статье Gödel 1932 Гёдель предложил простой аргумент, который показывает, что интуиционистскую пропозициональную логику нельзя рассматривать как конечнозначную логику. А именно, Гёдель доказал две теоремы:

Теорема 7. 

Не существует реализации с конечным числом элементов (значений истинности), для которых выполняются (то есть дают обозначенные значения для произвольного присваивания) те формулы и только те, которые доказуемы в H. 

H — интуиционистская пропозициональная логика, условно обозначаемая так в честь Гейтинга (Heyting).

Теорема 8.

Между Н и системой А обычного исчисления высказываний находится бесконечно много систем; иными словами, существует монотонно убывающая последовательность систем, каждая из которых включает Н в качестве подмножества и входит в А в качестве подмножества.

В своем доказательстве он рассматривал для каждого натурального числа n > 0 предложение

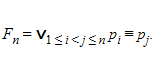
Он заметил, что в n-значной логике предложения Fm должны быть выводимыми для m > n. Однако Гёдель показал, что Fn не выводимо из аксиом Гейтинга для любого n.

Впоследствии Яськовский (Jaśkowski 1936) показал, что интуиционистской пропозициональной логике можно дать многозначную семантику посредством бесконечного числа истинностных значений. Дальнейший разбор многозначных логик см., напр., в статье о многозначной логике в этой энциклопедии, а также статью Ван Стигта об интуиционистской логике в Mancosu 1998.

2.5.2 Интерпретируемость классической арифметики в арифметике Гейтинга

Теперь рассмотрим статью (Gödel 1933e), в которой Гёдель показал, по сути, что интуиционистская или гейтинговская арифметика лишь на первый взгляд слабее классической арифметики первого порядка. Дело в том, что последнюю можно интерпретировать в первой посредством простого перевода, и, таким образом, чтобы убедиться в непротиворечивости классической арифметики, достаточно убедиться в непротиворечивости арифметики Гейтинга. Арифметика Гейтинга определяется как классическая арифметика за исключением того, что лежащая в ее основе логика предикатов задается интуиционистскими аксиомами и правилами вывода (см. ниже).

Этот результат приводит к тому же утверждению для пропозиционального случая. Обозначим через H интуиционистскую пропозициональную логику, а через A — ее классический аналог (как указано выше). Индуктивно определим:

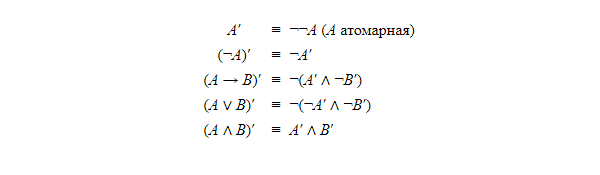
Тогда:

Теорема 9. 

Пусть F — пропозициональная формула. Тогда H ⊢ F, если и только если A ⊢ F′.

Теорему легко вывести из результата Glivenko 1929, согласно которому ¬F следует из H тогда и только тогда, когда ¬F следует из A для любой пропозициональной формулы F.

Так называемая интерпретация двойного отрицания Гёделя расширяет теорему 9 до редукции классической логики первого порядка к интуиционистской логике предикатов. В этом случае перевод можно произвести для отображения А' в А для атомарной А. Более того, пусть ∀xA(x)′ = ∀xA′(x): 

Теорема 10. 

Пусть А — формула первого порядка. Если A доказуема в классической логике первого порядка, то A' доказуема в интуиционистской логике первого порядка.

Вышеуказанный результат был получен независимо Генценом (с Бернайсом), но, услышав о результате Гёделя, Генцен снял свою статью с публикации. Его также предвидел Колмогоров в 1925 году в своей статье «О принципе tertium non datur» (Колмогоров 1925), но эта его статья была в основном неизвестна логикам, которые пребывали вне круга Колмогорова.

По словам Бернайса (см. статью Бернайса о Давиде Гильберте в Edwards 1967), данный результат Гёделя привлек внимание школы Гильберта к двум наблюдениям: во-первых, интуиционистская логика выходит за рамки финитизма, а во-вторых, финитистские системы не могут быть единственно приемлемыми с точки зрения оснований.

Из теоремы 10 вытекает следующая теорема для случая арифметики:

Теорема 11. 

Пусть А — формула первого порядка арифметики. Если A доказуема в классической арифметике Пеано, то A' доказуема в интуиционистской арифметике первого порядка. 

Список аксиом и правил интуиционистской логики первого порядка см. в Gödel 1958, переиздание с подробным вступительным примечанием А.С. Троэлстра см. в Gödel 1990. См. также Troelstra 1973 и «Аспекты конструктивной математики» Троэлстра в Barwise 1977. Подробное доказательство вышеуказанной теоремы читатель найдет в последнем материале.

Интерпретируемость интуиционистской пропозициональной логики в S4

Этот результат Гёделя (Gödel 1933), знаменующий начало логики доказуемости, устанавливает точное различие между понятиями «доказуемость в определенной формальной системе» и «доказуемость с помощью каких-либо надлежащих средств».

Гёдель уже отмечал это различие во введении к своей диссертации 1929 года. Контекст заключался в следующем: Гёдель считал, что его доказательство теоремы о полноте может основываться на порочном круге, так как для ее доказательства использовался закон исключенного среднего. Это связано с тем, что, хотя теорема о полноте утверждает «своего рода разрешимость», то есть каждая количественная формула либо доказуема, либо ей может быть дан контрпример, «принцип исключенного третьего, по-видимому, не выражает не что иное, как разрешимость каждой проблемы»:

Гёдель рассматривает интуиционистскую пропозициональную логику (далее IPL); он также рассматривает вторую систему, классическую пропозициональную логику, обогащенную оператором «В», где предполагаемым значением «В» является «доказуемо». Система аксиом, в настоящее время известная как S4 (список этих аксиом см. в статье о модальной логике), добавляется к стандартным аксиомам для классической логики высказываний вместе с новым правилом доказательства: из A может быть выведено BA. Назовем эту вторую систему G. Теорема Гёделя гласит, что IPL интерпретируется в G посредством следующего перевода:

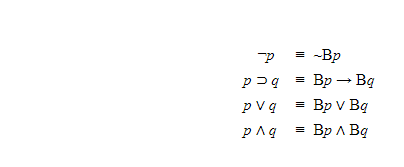
Таким образом:

Теорема 12. 

Пусть A — формула IPL и пусть A' — ее перевод. Тогда IPL ⊢ A подразумевает G ⊢ A'.

Гёдель предполагает, что обратная импликация должна быть истинной, и это действительно было показано в McKinsey and Tarski 1948.

Различие между двумя понятиями доказуемости — «доказуемость в рамках данной формальной системы S» и доказуемость любыми надлежащими средствами — проявляет себя в качестве следствия второй теоремы Гёделя о неполноте следующим образом. Пусть S содержит арифметику Пеано и оператор B интерпретируется как «доказуемо в S». Если аксиомы S4 справедливы для интерпретаций B, то, по B(0 ≠ 1) → (0 ≠ 1), предложение ¬B(0 ≠ 1) было бы доказуемо, что противоречило бы второй теореме о неполноте.

Дальнейшее обсуждение теоремы Гёделя, ее предшественников и ее расширений, а также ее философского значения см. во введении Троэлстра к статье Gödel 1933f.

Интерпретируемость арифметики Гейтинга в вычислимых функционалах конечного типа

Так называемая интерпретация «Диалектики» Гёделя (Gödel 1958) обеспечивает доказательство относительной непротиворечивости и обоснование гейтинговской арифметики посредством конкретной интерпретации, включающей систему T вычислимых функционалов конечного типа. Если взять ее вместе с публикацией Gödel 1933e, допускающей сведение классической арифметики первого порядка к гейтинговской арифметике, то подобное обоснование также было получено для классической арифметики первого порядка.

Индуктивное определение Гёделем понятия «функция конечного типа» заключается в следующем:

Функционалы 0-го типа являются натуральными числами. 

Если t0, …, tk представляют собой типы, и мы уже определили, каковы функционалы типов t0,…, tk, то (t0,…, tk) представляет собой тип, чей функционал присваивается каждому k-кортежу функционалов соответствующих типов t1,…, tk, и это функционал типа t0. 

(Gödel 1990: 245)

Гёдель рассматривает бескванторную теорию этих функционалов конечного типа, обозначаемую Т. Эта теория Т имеет следующие особенности: язык T содержит переменные каждого типа, постоянные для выделенных типов и трехместный предикат =σ равенства для типа σ. Равенство между термами одного и того же типа разрешимо. Внелогические аксиомы и правила для T включают аксиомы классической арифметики для 0 и следования, а также правило индукции:

для бескванторных формул F(x0). Как отмечает Гёдель (Gödel 1990, стр. 247), аксиомы для T по существу такие же, как и для примитивно-рекурсивной арифметики, за исключением того, что переменные могут быть любого конечного типа.

Перевод Гёделя связывает с каждой формулой F (x) языка арифметики Пеано формулу F'(x) = ∃y∀zA(y, z, x) языка теории T, где A является бескванторной и (выделенные полужирным шрифтом) связанные переменные представляют собой конечные последовательности переменных, пробегающих функционалы конечного типа и определяемые типом переменной. Интуитивно y является конкретным аналогом абстрактного понятия построения, конституирующего значение F.

Теорема Гёделя гласит:

Теорема 13. 

Пусть F′ = ∃y∀zA(y, z, x). Если F доказуемо в интуиционистской арифметике первого порядка, то существуют вычислимые функционалы Q конечного типа такие, что A(Q(x), z, x) доказуемо в T.

Доказательство проводится индукцией по структуре доказательства F в интуиционистской арифметике первого порядка. (Подробный разбор доказательства см. в Troelstra 1986.)

Невозможно переоценить важность этой теоремы для оснований математики. Однако обсуждение ее обобщений, последующих работ Крейзеля, Тейта, Говарда, Фефермана и др. над функциональными интерпретациями, вдохновленных ею; ее значения для оснований математики и для философии; и в конечном итоге ее отношения, в частности, к ее ранней неформальной доказательной интерпретации Гейтингом и Колмогоровым, здесь предпринято не будет. Соответственно, в литературе имеется множество работ по данной теме, см., напр., вышеупомянутые публикации Troelstra 1986, Tait 1967, Feferman 1993 и Avigad and Feferman 1998. Интересные недавние разработки, например, в области связывания интерпретации «Диалектики» Гёделя и модифицированной реализуемости Крайзеля отражены в Oliva 2006. См. также van Oosten 2008. 

Замечание относительно философского контекста, в котором Гёдель представил свой перевод, а именно финитизма. Вопрос, затронутый во введении к статье, заключается в том, какие абстрактные понятия должны быть добавлены к финитной математике, чтобы было получено доказательство непротиворечивости арифметики. Эквивалентно: какое из предположений финитной позиции следовало бы отбросить в свете второй теоремы о неполноте, если необходимо получить доказательство непротиворечивости:

В любом случае замечание Бернайса учит нас различать две составляющие финитного подхода. А именно, во-первых, конструктивный элемент, заключающийся в том, что нам разрешено говорить о математических объектах только постольку, поскольку мы можем их представлять или фактически производить с помощью построения. Во-вторых, особый финитистский элемент, который дополнительно требует, чтобы объекты, в отношении которых мы производим утверждения, с которыми выполняются построения и которые мы получаем с помощью этих построений, являлись «интуитивными», то есть представляли бы собой в конечном анализе пространственно-временные конфигурации элементов, характеристики которых, помимо их тождественности или нетождественности, не имели бы значения… <…> Именно второе требование необходимо отбросить. Данный факт ранее принимался во внимание нашей примыкающей к финитной математике частью интуиционистской логики и теорией порядковых чисел. В дальнейшем мы покажем, что для доказательства непротиворечивости теории чисел мы можем вместо этого использовать понятие вычислимой функции конечного типа на натуральных числах и некоторые достаточно элементарные принципы построения таких функций. (Gödel 1990: 245)

Публикация Gödel 1958/72 представляет собой не только сугубо технический вклад, но и одну из важнейших философских работ Гёделя; она примечательна своим анализом природы финитной математики, а также анализом понятий «интуитивный», как в «интуитивном знании», и оппозиции абстрактного и конкретного свидетельств. 

В следующем разделе мы обратимся к философским взглядам Гёделя.

Философские воззрения Гёделя

Философские взгляды Гёделя могут быть в целом охарактеризованы двумя сферами интересов или, говоря современным языком, обязательств (commitments). Во-первых, имеется в виду реализм, то есть вера в то, что математика является описательной наукой в том же смысле, что и эмпирические науки. Второе обязательство касается разновидности лейбницианского рационализма в философии; и в самом деле основное философское влияние на Гёделя в этом отношении и не только оказали Лейбниц, Кант и Гуссерль. (Дальнейшее обсуждение того, как эти философы повлияли на Гёделя, см. в van Atten and Kennedy 2003).

Термины «реализм Гёделя» и «рационализм Гёделя» должны быть предварены разъяснительным замечанием: нет единого воззрения, которое можно было бы связать с каждым из них. Гёделевский реализм претерпел сложные изменения с течением времени, как по характеру его онтологических заявлений, так и по степени приверженности им Гёделя. Подобным же образом рационализм Гёделя подвергся сложному развитию с течением времени — от предварительной версии его в начале к тому, что было признано его довольно сильной версией в 1950-х годах. Примерно в 1959-м и некоторое время спустя Гёдель объединил собственную рационалистическую программу разработки точной философии с феноменологическим методом, развитым Гуссерлем. 

Мы рассмотрим эти два направления мышления Гёделя ниже.

Рационализм Гёделя

Гёделевский рационализм уходит своими корнями в лейбницианские представления о том, что мир — не тот, который мы имманентно переживаем, а именно тот, который сам создает имманентный опыт, — совершенен и прекрасен, а потому рационален и упорядочен. Обоснование Гёделем этого убеждения частично опирается на индуктивное обобщение совершенства и красоты математики:

Рационализм связан с платонизмом, поскольку он направлен скорее на концептуальный аспект, чем на (реальный) мир. Некто использует индуктивные свидетельства… Математика имеет форму совершенства… Мы можем ожидать, что мир понятий будет совершенным, и, кроме того, эта объективная реальность прекрасна, блага и совершенна. (Wang 1996: 9.4.18)

Наши реальность и опыт в целом прекрасны и значимы — это тоже лейбницианская мысль. Мы должны судить о реальности по тому малому, что действительно знаем о ней. Поскольку эта малая часть, которую мы знаем благодаря понятиям, полностью оказывается столь прекрасной, то и реальный мир, о котором мы так мало знаем, также должен быть прекрасен. (Wang 1996: 9.4.20)

Хотя истоки веры Гёделя в рационализм имеют метафизический характер, его давние устремления в этой области всегда были практическими. То есть необходимо разработать точные методы в философии; превратить ее в точную науку или strenge Wissenschaft (строгую науку), если воспользоваться выражением Гуссерля.

На практике это означает принятие самого строгого из возможных взгляда на то, что составляет диалектическую основу для принятия утверждения; иными словами, в философских рассуждениях достигается тот уровень строгости, который свойственен математическим доказательствам. Формулировку воззрения — с некоторой феноменологической окрашенностью (см. ниже) — можно найти в Gödel Nachlass. Это список из четырнадцати пунктов, который Гёдель создал примерно в 1960 году под названием «Моя философская точка зрения». Здесь указаны две позиции списка:

Существуют систематические методы решения всех проблем (также в искусстве и т.п.). 

Существуют научные (точные) философия и теология, которые работают с понятиями наивысшей абстрактности; и это также очень полезно для науки. 

(Список был транскрибирован Шерил Доусон и опубликован в Wang 1996: 316.)

Ранняя концепция рационализма Гёделя отсылает к математической строгости и включает в себя понятие наличия подлинного доказательства, поэтому она в некотором смысле более радикальна, чем та, которой он придерживался позднее. Ее можно увидеть в действии в конце Гиббсовской лекции Гёделя после ряда аргументов в пользу реализма:

Конечно, я не утверждаю, что такого рода рассужденияравносильны реальному доказательству этого взгляда оприроде математики. Самое большее, что я могу утверждать, состояло бы в опровержении номиналистическоговзгляда, который рассматривает математику как состоящую лишь из синтаксических конвенций и их следствий.Больше того, я выдвинул сильные аргументы против болееобщего взгляда, что математика есть наше собственноетворение. Однако есть и другие альтернативы платонизму,в частности психологизм и аристотелевский реализм.Для установления платонистского реализма эти теорииследует опровергнуть одну за другой, и в этом случае будут исчерпаны все возможности. Я не в состоянии сделатьэто, однако я хотел бы наметить основные моменты в этомнаправлении. (Гёдель 1951: 198)

(Более глубокий анализ этого фрагмента см. в Tait 2001.) Такой анализ должен основываться на концептуальном анализе:

Я нахожусь под впечатлением, что после достаточногопрояснения упомянутых понятий будет возможно проводить подобные обсуждения с математической строгостью и что в результате… платонистский взгляд есть единственная приемлемая альтернатива. (Гёдель 1951: 199; пер. изм.)

Наряду с методологической составляющей, как видно из пунктов списка Гёделя, в рационализме Гёделя присутствовала также и «оптимистичная»: как только будут разработаны соответствующие методы, такие философские проблемы, как, например, вопросы этики (см., напр., позицию 9 в списке: «Формальные права составляют настоящую науку»), могут быть точно решены. Что касается математических утверждений, таких как континуум-гипотеза в теории множеств, то как только концептуальный анализ будет проведен правильно, то есть когда основные понятия, такие как «множество», будут полностью прояснены, континуум-гипотеза должна быть разрешена. 

Хотя во времена лекции Гиббса аналогия в понимании Гёделя между философским и математическим рассуждением, возможно, была очень близкой, и точка зрения Гёделя в другие периоды времени заключалась в том, что предполагаемые методы не будут иметь математическую природу. Необходима была общая неформальная наука концептуального анализа.

Философия имеет более общий характер, чем наука. Уже теория понятий имеет более общий характер, чем математика… Истинная философия является точной, но не специализированной. 

Возможная причина, по которой не достигнут прогресс в математике (и существует столь много нерешенных проблем), заключается в том, что она ограничивается экст[енсиональным], а отсюда следует чувство разочарования в случае многих теорий, например, пропозициональной логики и формализации вообще. (Wang 1996: 9.3.20, 9.3.21) 

(См. записную книжку Max IV: 198 (Gödel Nachlaß, Firestone Library, Princeton, item 030090). Транскрипция Шерил Доусон; перевод с немецкого наш; добавление наше. Гёдель датирует Max IV с мая 1941-го по апрель 1942-го. См. также письмо Гёделя Бернайсу, Gödel 2003a: 283.)

Важным источником для понимания продвижения Гёделя к общей теории понятий служат замечания Гёделя о концептуальном анализе, опубликованные Хао Ваном в «Логическом путешествии». Например, Гёдель выражает убеждение в том, что экстенсиональность не соответствует понятиям, вопреки тому замечанию, которое он высказал в «Расселовской математической логике» ранее (Гёдель 1942), и от которого он теперь желает отстраниться:

Я (больше) не верю, что тождества диапазона значений в целом достаточно, чтобы исключить раздельность двух понятий. (Wang 1996: 8.6.10)

В некоторых последующих обсуждениях Гёделя появляется еще одна составляющая концептуального анализа, а именно проект нахождения так называемых примитивных терминов или понятий и их отношений. Грубо говоря, это термины или понятия, которые составляют теоретическую «отправную точку» из-за своего полностью определенного и ясного значения. Например, понятие «применение понятия к другому понятию» является примитивным термином наряду с понятием «усилие» (Wang 1996: 9.1.29).

Он говорил Вану об общем проекте в 1972 году:

Феноменология — не единственный подход. Другой подход состоит в том, чтобы найти перечень основных категорий (напр., причинность, субстанция, действие) и их взаимосвязей, которые, однако, должны быть получены феноменологически. Задача должна быть выполнена надлежащим образом. (Wang 1996: 5.3.7)

Гёдель беседовал с Сью Толедо в период между 1972 и 1975 годами о проекте поиска примитивных терминов, а также других аспектах феноменологии. См. Toledo 2011.

Современные философы отнеслись к гёделевскому рационализму недоброжелательно (см., напр., Gödel 1995: 303–304). Однако сам Гёдель оставался настроен оптимистически. Как он заметил Вану:

Нельзя сказать, что философия как строгая наука не может быть реализована в обозримом будущем. Время не является решающим фактором; это может произойти в любое время, когда появляется правильная идея. (Wang 1996: 4.3.14)

Гёдель завершил свою статью о Расселе (Гёдель 1942) на схожей оптимистичной ноте.

Реализм Гёделя

Реалистические взгляды Гёделя были сформулированы главным образом в контексте оснований математики и теории множеств.

Мы упомянули выше список «Во что я верю», который, как полагают, был составлен в 1960 году или около того. Из 14 позиций лишь две обращаются к теме реализма, замечания 10 и 12:

Материализм ложен. 

Понятия имеют объективное существование. 

Гёдель впервые опубликовал свои взгляды на реализм в Гёдель 1942. Ниже приведено одно из его наиболее часто цитируемых утверждений на эту тему:

Классы и понятия могут, однако, рассматриватьсятакже и как реальные объекты, а именно классы — как«множественности вещей» или как структуры, состоящиеиз множественности вещей, а понятия — как свойства и отношения вещей, существующих независимо от нашихопределений и построений.

Мне кажется, что предположения о таких объектахстоль же допустимы, как и предположения о физическихтелах, и имеется столь же много причин верить в их существование. Они в том же самом смысле необходимы дляполучения удовлетворительной системы математики, какфизические тела необходимы для получения удовлетворительной теории наших чувственных восприятий, и в обоихслучаях невозможно интерпретировать пропозиции, которые мы желаем утверждать о таких сущностях, как пропозиции о «данных», то есть в последнем случае как о действительно наличествующих чувственных восприятиях. (Гёдель 1942: 142–143; пер. изм.)

Ссылка Гёделя на невозможность интерпретации эмпирических законов, а точнее, их инстанциаций — положений, «которые мы желаем утверждать», — как положений, касающихся чувственных восприятиях, по всей вероятности является свидетельствует о его приверженности современной (ему) критики феноменализма. Критика опиралась на наблюдение, что чувственные данные настолько неразрывно связаны с условиями, в которых они переживаются, что не может быть соответствия между заявлениями о них и заявлениями вида «мы желаем утверждать» (см., напр., Chisholm 1948). В более общем плане Гёдель выступал против верификационизма, а именно представления о том, что значение утверждения — это его способ верификации.

Аналогичная позиция в первой части утверждения была усилена Гёделем в черновике рукописи «Является ли математика синтаксисом языка?»:

Трактовка формулировок типа «это красное» как касающихся непосредственных данных является произвольной, но нельзя с той же произвольностью трактовать пропозицию, выражающую modus ponens или полную индукцию (или, возможно, некоторые более простые пропозиции, из которых следуют последние). (Gödel 1995: 359)

Некоторые авторы интерпретировали эти и схожие пассажи Гёделя прагматически, приписывая ему мнение, согласно которому, поскольку эмпирические утверждения служат парадигмальным примером успешной референции, референция для абстрактных понятий должна быть смоделирована каузально. (См. Maddy 1990.) Утверждается, что такая интерпретация указания на абстрактные объекты преодолевает основные трудности, связанные с реализмом, а именно сложность получения знаний об абстрактных объектах. Другие утверждали, что Гёдель не имел в виду парадигмальный пример и что для него как эмпирический, так и абстрактный случаи либо одинаково проблематичны, либо одинаково беспроблемны. (См. Tait 1986.) Последний взгляд именуется эпистемологическим паритетом в van Atten and Kennedy 2003. (См. также Kennedy и van Atten 2004.)

В своей работе 1947-го «Что такое проблема континуума Кантора?» Гёдель излагает мнение о том, что в случае значимых пропозиций математики всегда имеется вопрос, который должен решаться по принципу «да» или «нет». Это прямое следствие реализма, ведь если существует область математических объектов или понятий, тогда любая содержательная пропозиция по поводу них должна быть либо истинной, либо ложной. Континуум-гипотеза — пример значимого вопроса по Гёделю. Понятие «сколько» приводит «однозначно» к определенному значению (meaning) гипотезы, и поэтому оно должно быть разрешимым — по крайней мере в принципе. Что наиболее поразительно, Гёдель не останавливается на этом и предлагает практическую стратегию установления значения (value) континуума, а также значения истинности других аксиом, расширяющих ZFC. В частности, он предлагает два критерия для их разрешимости: первый предполагает концептуальный анализ и связан с рационалистической программой Гёделя. (См. выше раздел о рационализме Гёделя.) Во-вторых, нужно держать в поле зрения так называемую успешность аксиомы в качестве удостоверения или показателя того, в каком направлении следует искать решение ее истинности. Например, Гёдель отмечает в своей статье, что ни одно из следствий аксиомы конструируемости не является достаточно правдоподобным. В таком случае, по всей вероятности, они ложны. Обсуждение внутренних (intrinsic) и внешних (extrinsic) обоснований новых аксиом теории множеств см. в Maddy 2011 и Koellner 2014. 

Библиография

Сочинения Гёделя

Избранные работы на русском языке

Гёдель К. (1933) Современное положение дел в основаниях математики // Хинтикка Я., Гёдель К. О Гёделе. Статьи. М.: Канон+, 2014. С. 108–124.

–—. (1944) Расселовская математическая логика // Хинтикка Я., Гёдель К. О Гёделе. Статьи. М.: Канон+, 2014. С. 125–165.

–—. (1951) Некоторые основные теоремы в основаниях математики и их следствия // Хинтикка Я., Гёдель К. О Гёделе. Статьи. М.: Канон+, 2014. С. 166–200.

–—. (1961) Современное развитие оснований математики в свете философии // Хинтикка Я., Гёдель К. О Гёделе. Статьи. М.: Канон+, 2014. С. 201–211.

Избранные работы на других языках

(1929) “I”, Dissertation, University of Vienna. Reprinted in Gödel 1986, pp. 60–101.

(1930) “Die Vollständigkeit der Axiome des logischen Functionenkalküls”, Monatshefte für Mathematik und Physik, 37: 349–360. Reprinted in Gödel 1986, pp. 102–123.

(1931) “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I”, Monatshefte für Mathematik und Physik, 38: 173–198. Reprinted in Gödel 1986, pp. 144–195.

(1932) “Zum intuitionistischen Aussagenkalkül”, Anzeiger der Akademie der Wissenschaften in Wien, 69: 65–66. Reprinted in Gödel 1986, pp. 222–225.

(1933e) “Zur intuitionistischen Arithmetik und Zahlentheorie”, Ergebnisse eines mathematischen Kolloquiums, 4: 34–38. Reprinted in Gödel 1986, pp. 286–295.

(1933f) “Eine Interpretation des intuitionistischen Aussagenkalküls”, Ergebnisse eines mathematischen Kolloquiums 4, 39–40. Reprinted in Gödel 1986, pp. 300–301.

(1933i) “Zum Entscheidungsproblem des logischen Functionenkalküls”, Monatshefte für Matematik und Physik, 40: 433–443. Reprinted in Gödel 1986, pp. 306–326.

(1934c) Review of Skolem (1933). Zentralblatt für Mathematik und ihre Grenzgebiete, 7: 193–194. Reprinted in Gödel 1986, pp. 379–380.

(1936a) “Über die Länge von Beweisen”, Ergebnisse eines mathematischen Kolloquiums, 7: 23–24. Reprinted in Gödel 1986, pp. 395–399.

(1939a) “Consistency proof for the generalized continuum hypothesis”, Proceedings of the National Academy of Sciences, U.S.A., 25: 220–224. Reprinted in Gödel 1990, pp. 28–32.

(1940) “The Consistency of the Continuum Hypothesis”, Annals of Mathematics Studies, Volume 3, Princeton: Princeton University Press. Reprinted in Gödel 1990, pp. 33–101.

(*1941) “In what sense is intuitionistic logic constructive?”, lecture manuscript. Printed in Gödel 1995, pp. 189–200.

(*1946/9-B2) “Some observations about the relationship between theory of relativity and Kantian philosophy”, manuscript. Printed in Gödel 1995, pp. 230–246.

(*1946/9-C1) “Some observations about the relationship between theory of relativity and Kantian philosophy”, manuscript. Printed in Gödel 1995, pp. 247–259.

(1947) “What is Cantor's continuum problem?”, Amer. Math. Monthly, 54: 515–525. Reprinted in Gödel 1990, pp. 176–187.

(1949a) “A remark on the relationship between relativity theory and idealistic philosophy”, Albert Einstein: Philosopher-Scientist (Library of Living Philosophers), P. Schilpp (ed.), La Salle, IL: Open Court, 1949, pp. 555–562. Reprinted in Gödel 1990, pp. 202–207.

(1949) “An Example of a New Type of Cosmological Solutions of Einstein's Field Equations of Gravitation,” Reviews of Modern Physics, 21: 447–450. Reprinted in Gödel 1990, pp. 190–198.

(*1953/9-III) “Is mathematics a syntax of language?”, lecture manuscript. Printed in Gödel 1995, pp. 334–356.

(*1953/9-V) “Is mathematics a syntax of language?,” lecture manuscript. Printed in Gödel 1995, pp. 356–362.

(1958) “Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes”, Dialectica, 12: 280–287. Reprinted in Gödel 1990, pp. 240–251.

(1964) “What is Cantor's continuum problem?”, revised version of Gödel 1947, in Benacerraf, P. and Putnam, H. (eds.), 1983, Philosophy of mathematics: selected readings (2nd ed.), Cambridge: Cambridge University Press. Reprinted in Gödel 1990, pp. 254–270.

(*1970) “Ontological proof”, manuscript. Printed in Gödel 1995, pp. 403–404.

(*1970a) “Some considerations leading to the probable conclusion that the true power of the continuum is ℵ2”, manuscript. Printed in Gödel 1995, pp. 420–422.

(*1970b) “A proof of Cantor's continuum hypothesis from a highly plausible axioms about orders of growth”, manuscript. Printed in Gödel 1995, pp. 422–423.

Собрание сочинений на английском языке

1986, Collected Works. I: Publications 1929–1936. S. Feferman, S. Kleene, G. Moore, R. Solovay, and J. van Heijenoort (eds.), Oxford: Oxford University Press.

1990, Collected Works. II: Publications 1938–1974. S. Feferman, J. Dawson, S. Kleene, G. Moore, R. Solovay, and J. van Heijenoort (eds.), Oxford: Oxford University Press.

1995, Collected Works. III: Unpublished essays and lectures. S. Feferman, J. Dawson, S. Kleene, G. Moore, R. Solovay, and J. van Heijenoort (eds.), Oxford: Oxford University Press.

2003a, Collected Works. IV: Correspondence A-G. S. Feferman, J. Dawson, S. Kleene, G. Moore, R. Solovay, and J. van Heijenoort (eds.), Oxford: Oxford University Press.

2003b, Collected Works. V: Correspondence H-Z. S. Feferman, J. Dawson, S. Kleene, G. Moore, R. Solovay, and J. van Heijenoort (eds.), Oxford: Oxford University Press.

Другие источники

Больцано Б. (2003) Учение о науке (избранное). М.: Наука. §§ 349–391.

Гильберт Д. (1948) О бесконечном // Он же. Основания геометрии. М.; Л.: Гостехиздат. С. 338–364.

Гильберт Д., Аккерман В. (2010) Основы теоретической логики. М.: Издательская группа URSS.

Гильберт Д., Бернайс П. (1979) Основания математики. М.: Наука. Т. 1: Логические исчисления и формализация арифметики.

–—. (1982) Основания математики. М.: Наука. Т. 2: Теория доказательств.

Гуссерль Э. (1994) Философия как строгая наука. Новочеркасск: Агентство «Сагуна».

Колмогоров А.Н. (1925) О принципе tertium non datur // Математический сборник. Т. 32. № 4. С. 646–667.

Avigad, J. and S. Feferman, 1998, “Gödel's Functional (‘Dialectica’) Interpretation”, in Handbook of Proof Theory (Studies in Logic and the Foundations of Mathematics, Volume 137), Samuel Buss (ed.), Amsterdam: North-Holland, pp. 337-405.

Awodey, S. and A. W. Carus, 2010, “Gödel and Carnap”, in Kurt Gödel: Essays for his Centennial, Solomon Feferman, Charles Parsons & Stephen G. Simpson (eds.), Cambridge: Cambridge University Press.

Baaz, M., and C. Papadimitriou, D.Scott, H. Putnam, and C. Harper (eds.), 2011, Kurt Gödel and the Foundations of Mathematics: Horizons of Truth, Cambridge: Cambridge University Press.

Badesa, C., and P. Mancosu, and R. Zach, 2009, “The Development of Mathematical Logic from Russell to Tarski, 1900–1935”, in Leila Haaparanta (ed.), The History of Modern Logic. New York and Oxford: Oxford University Press:318–470..

Barwise, Jon (ed.), 1977, Handbook of Mathematical Logic (Studies in Logic and the Foundations of Mathematics, Volume 90), Amsterdam: North-Holland Publishing Co.

Behmann, Heinrich, 1922, “Beiträge, Algebra, Logik, insbesodere zum Entscheidungsproblem”, Mathematische Annalen, 86: 419–432.

Benacerraf, P. and H. Putnam (eds.), 1983, Philosophy of Mathematics: Selected Readings, Cambridge: Cambridge University Press, 2nd edition.

Bernays, Paul, 1926, “Axiomatische Untersuchung des Aussagen-Kalkuls der ‘Principia Mathematica’”, Mathematisches Zeitschrift, 25(1): 305–320.

Bezboruah, A., and J.C. Sheperdson, 1976, “Gödel's second incompleteness theorem for Q”, Journal of Symbolic Logic, 41 (2): 503–512.

Burgess, John, 2009, “”Intuitions of Three Kinds in Gödel's Views on the Continuum“”, in Interpreting GödelKennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Buss, Samuel R., 1994, “On Gödel's Theorems on Lengths of Proofs. I. Number of Lines and Speedup for Arithmetics”, Journal of Symbolic Logic, 59(3): 737–756.

Chisholm, R., 1948, “The Problem of Empiricism”, The Journal of Philosophy, 45: 512–7.

Cohen, Paul, 1963, “The Independence of the Continuum Hypothesis”, Proceedings of the National Academy of Sciences of the U.S.A., 50: 1143–1148.

Crocco, G., 2003, “Gödel, Carnap and the Fregean Heritage”, History and Philosophy of Logic, 27: 171–191.

–––, 2006, “Gödel on Concepts”, Synthese, 137(1,2): 21–41.

Dawson, Jr., John W., 1997, Logical dilemmas: The Life and Work of Kurt Gödel, Wellesley, MA: A. K. Peters, Ltd.

Dehornoy, Patrick, 2004, “Progrès récents sur l'hypothèse du continu (d'après Woodin)”, Astérisque, 294: viii, 147–172.

Detlefsen, Michael, 1986, Hilbert's Program: An essay on mathematical instrumentalism, Dordrecht: D. Reidel.

–––, 2001, “What Does Gödel's Second theorem Say?”, Philosophia Mathemathica, 9(1): 37–71.

–––, 2014, “Completeness and the Ends of Axiomatization”, in Interpreting Gödel, Kennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Dreben, B. and J. van Heijenoort, 1986, “Introductory Note to 1929, 1930 and 1930a”, in Gödel 1986, pp. 44–59.

Edwards, Paul (ed.), 1967, The Encyclopedia of Philosophy, New York: MacMillan.

Ehrenfeucht, A. and J. Mycielski, 1971, “Abbreviating Proofs by Adding New Axioms”, Bulletin of the American Mathematical Society, 77: 366–367.

Feferman, Solomon, 1960/1961, “Arithmetization of Metamathematics in a General Setting”, Fundamenta Mathematicae, 49: 35–92.

–––, 1993, “Gödel's Dialectica Interpretation and Its Two-way Stretch”, in Computational Logic and Proof Theory (Lecture Notes in Computer Science, Volume 713), G. Gottlob, A. Leitsch, and D. Mundici (eds.), Berlin: Springer, pp. 23–40.

–––, 1986, “Gödel's Life and Work”, in Gödel 1986, pp. 1–34.

–––, 1988, “Hilbert's Program Relativized: Proof-Theoretical and Foundational Reductions”,Journal of Symbolic Logic, 53: 364–384.

–––, 1996, “Proof Theory”, in The Encyclopedia of Philosophy Supplement, D. Borchrt (ed.), New York: MacMillan, pp. 466–469.

Feferman, S., and H. Friedman, P. Maddy, and J. Steel, 2000, “Does Mathematics Need New Axioms?”, Bulletin of Symbolic Logic, 6(4): 401–446.

Feferman, S., C. Parsons, and S. Simpson (eds.), 2010, Kurt Gödel: Essays for his Centennial(Lecture Notes in Logic, 33), Cambridge: Cambridge University Press.

Feigl, H. and A. Blumberg, 1931, “Logical Positivism. A New Movement in European Philosophy”, Journal of Philosophy, 28: 281–296.

Floyd, J. and A. Kanamori, 2006, “How Gödel Transformed Set Theory”, Notices of the American Mathematical Society, 53(4): 419–427.

Folina, Janet, 2014, “Gödel on How to Have your Mathematics and Know it Too”, in Interpreting Gödel, Kennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Føllesdal, Dagfinn, 1995, “Gödel and Husserl”, in From Dedekind to Gödel (Synthese Library, Volume 251), J. Hintikka (ed.), Dordrecht, Boston: Kluwer, pp. 427–446.

Foreman, Matthew, 1998, “Generic Large Cardinals: New Axioms for Mathematics?”, in Documenta Mathematica, Extra Volume, Proceedings of the International Congress of Mathematicians, II, pp. 11–21 [available online (in compressed Postscript)].

Franks, Curtis, 2009, “The Autonomy of Mathematical Knowledge: Hilbert's Program Revisited”, Cambridge: Cambridge University Press.

–––, 2011, “Stanley Tennenbaum's Socrates”, in Set Theory, Arithmetic and Foundations of Mathematics: Theorems, Philosophies, Kennedy, J. and Kossak, R., (eds.), Lecture Notes in Logic, 36, Cambridge: Cambridge University Press, 2011.

–––, 2014, “Logical Completeness, Form and Content: An Archaeology”, in Interpreting Gödel, Kennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Gaifman, H., 2000, “What Godel's Incompleteness Result Does and Does Not Show”, Journal of Philosophy, 97 (8): 462–471.

Garson, James, 2003, “Modal Logic”, in The Stanford Encyclopedia of Philosophy, Fall 2003 Edition, Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/fall2003/entries/logic-modal/>.

Glivenko, V., 1929, “Sur quelques points de la logique de m. Brouwer.”, Académie Royale de Belgique, Bulletin de la Classe des Sciences, 15: 183–188.

Gottwald, Siegfried, 2004, “Many-valued Logic”, in The Stanford Encyclopedia of Philosophy, Winter 2004 Edition, Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/win2004/entries/logic-manyvalued/>.

Gödel, Rudolf, 1983, “History of the Gödel Family”, Susan Simonsin (trans.), in Weingartner and Schmetterer 1987, pp. 11–27.

Hauser, Kai, 2006, “Gödel's Program Revisited, Part 1: the Turn to Phenomenology”, Bulletin of Symbolic Logic, 12 (4): 529–590.

Heyting, Arendt, 1930, “Die formalen Regeln der intuitionistischen Logik”, Sitzungsberichte der Preussischen Akademie der Wissenschaften, physikalisch-mathematische Klasse, II, pp. 42–56.

Hodges, Wilfrid, 2005, “Model Theory”, in The Stanford Encyclopedia of Philosophy, Fall 2005 Edition, Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/fall2005/entries/model-theory/>.

Jaśkowski, Stanisław, 1936, “Investigations into the System of Intuitionist Logic”, Studia Logica, 34(2) (1975): 117–120. (Translated by S. McCall from the French “Rechereches sur le système de la logique intuitioniste” in Actes du Congrés International de Philosophie Scientifique, Volume VI, Hermann, Paris, 1936, pp. 58–61.)

Jech, Thomas, 2003, Set theory, (Springer Monographs in Mathematics), Berlin: Springer-Verlag. 3rd millennium edition, revised and expanded.

Jensen, R. Björn, 1972, “The Fine Structure of the Constructible Hierarchy” (with a section by Jack Silver), Annals of Mathematical Logic, 4: 229–308; Erratum, 4 (1972): 443.

Kanamori, Aki, 1996, “The Mathematical Development of Set theory from Cantor to Cohen.” Bulletin of Symbolic Logic, 2(1): 1–71.

–––, 2006, “Levy and Set Theory”, Annals of Pure and Applied Logic, 140(3): 233–252.

Kennedy, Juliette, 2006, “Incompleteness — A Book Review,” Notices of the American Mathematical Societ, 53(4): 448–455.

–––, 2011, “Gödel's Thesis: An Appreciation” in Kurt Gödel and the Foundations of Mathematics: Horizons of Truth, M. Baaz, C. Papadimitriou, D. Scott, H. Putnam, and C. Harper (eds.), Cambridge: Cambridge University Press 95–110.

–––, 2013, “On Formalism Freeness: Implementing Gödel's 1946 Princeton Bicentennial Lecture”,Bulletin of Symbolic Logic, 19(3): 351–393.

–––, 2014, “Gödel's 1946 Princeton Bicentennial Lecture: An Appreciation”, in Interpreting Gödel: Critical Essays, Cambridge: Cambridge University Press.

Kennedy, Juliette (ed.), 2014, Interpreting Gödel: Critical Essays, Cambridge: Cambridge University Press.

Kennedy, J. and van Atten, M., 2003, “On the Philosophical Development of Kurt Gödel”, Bulletin of Symbolic Logic, 9(4): 425–476. Reprinted in Kurt Gödel: Essays for his Centennial, Solomon Feferman, Charles Parsons and Stephen G. Simpson (eds.), Cambridge: Cambridge University Press.

–––, 2004, “Gödel's Modernism: On Set-theoretic Incompleteness”, Graduate Faculty Philosophy Journal, 25(2): 289–349. (See the Erratum in Graduate Faculty Philosophy Journal, 26(1) (2005), page facing contents.)

–––, 2009, “Gödel's Modernism: On Set-theoretic Incompleteness, Revisited”, in Logicism, Intuitionism and Formalism: What has become of them?, S. Linström, E. Palmgren, K. Segerberg, and V. Stoltenberg-Hansen (eds.), Berlin: Springer: 303–356.

–––, 2009, “Gödel's Logic”, in D. Gabbay and J. Woods (eds.), The Handbook of the History of Logic: Logic from Russell to Gödel, Volume 5, Amsterdam: Elsevier: 449–509.

Kleene, S. C., 1987, “Gödel's Impression on Students of Logic in the 1930s”, in Weingartner and Schmetterer 1987, pp. 49–64.

Koellner, Peter, 2014, “Large Cardinals and Determinacy”, The Stanford Encyclopedia of Philosophy (Spring Edition), Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/spr2014/entries/large-cardinals-determinacy/>.

Kreisel, Georg, 1980, “Kurt Gödel, 28 April 1906 – 14 January 1978”, Biographical Memoirs of Fellows of the Royal Society, 26: 148–224. Corrigenda, 27 (1981): 697; further corrigenda, 28 (1982): 697.

–––, 1988, “Review of Kurt Gödel: Collected works, Volume I”, Notre Dame Journal of Formal Logic, 29(1): 160–181.

–––, 1990, “Review of Kurt Gödel: Collected Works, Volume II”, Notre Dame Journal of Formal Logic, 31(4): 602–641.

–––, 1998, “Second Thoughts Around Some of Gödel's Writings: A Non-academic Option”, Synthese, 114(1): 99–160.

Kripke, Saul, 2009, “The collapse of the Hilbert program: why a system cannot prove its own 1-consistency”, Bulletin of Symbolic Logic, 15 (2): 229–231.

Kunen, Kenneth, 1983, Set Theory: An Introduction to Independence Proofs, (Studies in Logic and the Foundations of Mathematics, Volume 102), Amsterdam: North-Holland Publishing Co. Reprint of the 1980 original.

Löb, M. H., 1956, “Formal Systems of Constructive Mathematics”, Journal of Symbolic Logic, 21: 63–75.

Löwenheim, L., 1915, “Über Möglichkeiten im Relativkalkül”, Mathematische Annalen, 76(4): 447–470.

Łukasiewicz, Jan, 1970, Selected works, (Studies in Logic and the Foundations of Mathematics), L. Borkowski (ed.), Amsterdam: North-Holland Publishing Co.

Maddy, Penelope, 1990, Realism in Mathematics, New York: Clarendon Press.

Maddy, Penelope, 2011, Defending the Axioms, Oxford: Oxford University Press.

Mal'cev, Anatoli Ivanovic, 1971, The Metamathematics of Algebraic Systems. Collected Papers: 1936–1967 (Studies in Logic and the Foundations of Mathematics, Volume 66), translated, edited, and provided with supplementary notes by Benjamin Franklin Wells, III, Amsterdam: North-Holland Publishing Co.

Mancosu, Paolo, 1998, From Brouwer to Hilbert. The Debate on the Foundations of Mathematics in the 1920s, Oxford: Oxford University Press.

–––, 2004, “Review of Kurt Gödel, Collected Works, Volumes IV and V”, Notre Dame Journal of Formal Logic, 45: 109–125.

Martin, D.A., 2005, “Gödel's Conceptual Realism”, Bulletin of Symbolic Logic, 11: 207–224.

McKinsey, J. C. C. and A. Tarski, 1948, “Some Theorems About the Sentential Calculi of Lewis and Heyting”, Journal of Symbolic Logic, 13: 1–15.

Mostowski, Andrzej, 1949, “An Undecidable Arithmetical Statement”, Fundamenta Mathematicae, 36: 143–164.

–––, 1982, Sentences Undecidable in Formalized Arithmetic: An Exposition of the Theory of Kurt Gödel, Westport, CT: Greenwood Press. Reprint of the 1952 original.

Oliva, Paulo, 2006, “Unifying Functional Interpretations”, Notre Dame Journal of Formal Logic, 47(2): 263–290.

Parikh, Rohit, 1971, “Existence and Feasibility in Arithmetic”, Journal of Symbolic Logic, 36: 494–508.

Parsons, Charles, 1995a, “Platonism and Mathematical Intuition in Kurt Gödel's Thought”, Bulletin of Symbolic Logic, 1(1): 44–74.

–––, 1995b, “Quine and Gödel on Analyticity”, in On Quine: New Essays, Cambridge: Cambridge University Press, pp. 297–313.

–––, 2000, “Reason and Intuition”, Synthese, 125(3): 299–315.

–––, 2002, “Realism and the Debate on Impredicativity, 1917–1944”, in Reflections on the Foundations of Mathematics: Essays in Honor of Solomon Feferman, (Lecture Notes in Logic, Volume 15), W. Sieg, R. Sommer, and C. Talcott (eds.), Urbana, IL: Association of Symbolic Logic, pp. 372–389.

–––, 2010, “Gödel and Philosophical Idealism”Philosophia Mathematica, 18 (2): 166–192.

–––, 2014, “Analyticity for Realists”, in Interpreting Gödel, Kennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Poonen, Bjorn, 2014, “Undecidable Problems: A Sampler”, in Interpreting Gödel: Critical Essays, Cambridge: Cambridge University Press.

Post, Emil L., 1921, “Introduction to a General Theory of Elementary Propositions”, American Journal of Mathematics, 43(3): 163–185.

Pudlák, Pavel, 1996, “On the lengths of proofs of consistency: a survey of results”, Annals of the Kurt Gödel Society, 2: 65-86.

Raatikainen, P., 2005, “On the Philosophical Relevance of Gödel's Incompleteness Theorems”, Revue Internationale de Philosophie, 59 (4): 513–534.

Rogers, Jr., Hartley, 1967, Theory of Recursive Functions and Effective Computability, New York: McGraw-Hill Book Co.

Rosser, J.B., 1936, “Extensions of Some Theorems of Gödel and Church”, Journal of Symbolic Logic, 1(3): 87–91.

Scott, Dana, 1961, “Measurable Cardinals and Constructible Sets”, Bulleint de l'Academie Polonaise des Sciences (Série des Science, Mathématiques, Astronomiques et Physiques), 9: 521–524.

Shelah, Saharon, 2014, “Reflecting on Logical Dreams”, in Interpreting Gödel: Critical Essays, Cambridge: Cambridge University Press.

Sieg, Wilfried, 1988, “Hilbert's Program Sixty Years Later”, Journal of Symbolic Logic, 53(2): 338–348.

–––, 1990, “Relative Consistency and Accessible Domains”, Synthese, 84(2): 259–297.

–––, 1999, “Hilbert's Programs: 1917–1922”, Bulletin of Symbolic Logic, 5(1): 1–44.

–––, 2006, “Gödel on Computability”, Philosophia Mathematica, 14: 189–207.

Sierpinski, Wacław, 1947, “L'hypothèse généralisée du continu et l'axiome du choix”, Fundamenta Mathematicae, 34: 1–5.

Sigmund, Karl, 2006, “Pictures at an Exhibition”, Notices of the American Mathematical Society, 53(4): 428–432.

Skolem, Thoralf, 1920, “Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeit mathematischer Sätze nebst einem Theoreme über dichte Mengen”, Skrifter utgit av Videnskappsselskapet i Kristiania, I. Matematisk-naturvidenskabelig klasse, Number 4, pp. 1–36. Reprinted in Skolem 1970, pp. 103–136.

–––, 1923, “Einige Bemerkungen zur axiomatischen Begründung der Mengenlehre”, Matematikerkongressen i Helsingfors den 4–7 Juli 1922, Den femte skandinaviska matematikerkongressen, Redogörelse, Helsinki, pp. 217–232. Reprinted in Skolem 1970, pp. 137–152.

–––, 1933, “Über die Unmöglichkeit einer vollständigen Charakterisierung der Zahlenreihe mittels eines endlichen Axiomensystems”, Norsk Matematisk forenings skrifter, 10: 73–82.

–––, 1970, Selected Works in Logic, Jens Erik Fenstad (ed.), Oslo: Universitetsforlaget.

Smith, David Woodruff, 2005, “Phenomenology”, in The Stanford Encyclopedia of Philosophy(Winter Edition), Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/win2005/entries/phenomenology/>.

Solovay, Robert, 1990, “Introductory Note to 1938, 1939, 1939a, 1940”, in Gödel 1990, pp. 1–25.

Steel, John, 2000, “Mathematics Needs New Axioms”, Bulletin of Symbolic Logic, 6(4): 422–433.

Steel, John, 2014, “Gödel's Program”, in Interpreting Gödel, Kennedy, J. (ed.) Cambridge: Cambridge University Press, 2014.

Tait, William, 1967, “Intensional Interpretations of Functionals of Finite Type I,” Journal of Symbolic Logic, 32(2): 198–212.

–––, 1981, “Finitism”, Journal of Philosophy, 78: 524–556. Reprinted in Tait 2005, pp. 21–42.

–––, 1986, “Truth and Proof: The Platonism of Mathematics”, Synthese, 69(3): 341–370. Reprinted in Tait 2005, pp. 61–88.

–––, 2001, “Gödel's Unpublished Papers on Foundations of Mathematics”, Philosophia Mathematica, 9(1): 87–126. Reprinted in Tait 2005, pp. 276–313.

–––, 2002, “Remarks on Finitism”, in Reflections on the Foundations of Mathematics: Essays in Honor of Solomon Feferman (Lecture Notes in Logic, Volume 15), W. Sieg, R. Sommer, and C. Talcott (eds.), Urbana, IL: Association of Symbolic Logic, pp. 410–419. Reprinted in Tait 2005, pp. 43–53.

–––, 2005, The Provenance of Pure Reason: Essays in the Philosophy of Mathematics and its History (Logic and Computation in Philosophy), New York: Oxford University Press.

–––, 2006, “Gödel's correspondence on proof theory and constructive mathematics”Philosophia Mathematica, 14 (1): 76–111.

–––, 2006, “Gödel's interpretation of intuitionism”,Philosophia Mathematica, 14 (2): 208–228.

Taussky-Todd, Olga, 1983, “Remembrances of Kurt Gödel”, in Weingartner and Schmetterer 1987, pp. 29–41.

Tieszen, Richard, 1992, “Kurt Gödel and Phenomenology”, Philosophy of Science, 59(2): 176–194.

–––, 2002, “Gödel and the Intuition of Concepts”, Synthese, 133 (3): 363–391.

–––, 2005, Phenomenology, Logic and the Philosophy of Mathematics, Cambridge: Cambridge University Press.

–––, 2011, After Gödel: Platonism and Rationalism in Mathematics and Logic, Oxford: Oxford University Press.

Toledo, Sue, 2011, “Sue Toledo's Notes of her Conversations with Kurt Gödel in 1972-5”, in Set Theory, Arithmetic and Foundations of Mathematics: Theorems, Philosophies (Lecture Notes in Logic, 36), Kennedy, J. and Kossak, R., (eds.), Cambridge: Cambridge University Press, forthcoming.

Tragesser, Robert, 1977, Phenomenology and Logic, Ithaca: Cornell University Press.

–––, 1984, Husserl and Realism in Logic and Mathematics, (Series: Modern European Philosophy), Cambridge: Cambridge University Press.

–––, 1989, “Sense Perceptual Intuition, Mathematical Existence, and Logical Imagination”, Philosphia Mathematica, 4(2): 154–194.

Troelstra, A. S., 1986, “Note to 1958 and 1972”, in Gödel 1990, pp. 217–241.

Troelstra, A. S. (ed.), 1973, Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, (Lecture Notes in Mathematics, Volume 344), Berlin: Springer-Verlag.

Turing, A. M., 1937, “On Computable Numbers, with an Application to the Entscheidungsproblem”, Proceedings of the London Mathematical Society (Series 2), 42: 230–265.

van Atten, Mark, 2005, “On Gödel's Awareness of Skolem's Helsinki Lecture”, History and Philosophy of Logic, 26(4): 321–326.

–––, 2006, “Two Draft Letters from Gödel on Self-knowledge of Reason”, Philosophia Mathematica, 14(2): 255–261.

–––, 2015, “Essays on Gödel's Reception of Leibniz, Husserl and Brouwer”, Springer.

van Heijenoort, J. (ed.), 1967, From Frege to Gödel: A sourcebook in mathematical logic, 1879–1931, Cambridge, MA: Harvard University Press.

van Oosten, Jaap, 2008, Realizability: An Introduction to its Categorical Side (Studies in Logic and Foundations of Mathematics: Volume 152), Amsterdam: Elsevier.

von Neumann, John, 2005, John von Neumann: Selected Letters (History of Mathematics, Volume 27), foreword by P. Lax, introduction by Marina von Neumann Whitman, preface and introductory comments by Miklós Rédei (ed.), Providence, RI: American Mathematical Society.

Väänänen, Jouko, 2014, “Multiverse Set Theory and Absolutely Undecidable Propositions”, in Interpreting Gödel, J. Kennedy (ed.), Cambridge: Cambridge University Press, 2014.

Wang, Hao, 1957, “The Axiomatization of Arithmetic”, Journal of Symbolic Logic, 22: 145–158.

–––, 1973, From Mathematics to Philosophy, London: Routledge.

–––, 1981, “Some Facts about Kurt Gödel”, Journal of Symbolic Logic, 46(3): 653–659.

–––, 1987, Reflections on Kurt Gödel, Cambridge, MA: MIT Press.

–––, 1993, Popular Lectures on Mathematical Logic, New York: Dover Publications Inc., 2nd edition.

–––, 1996, A Logical Lourney: From Gödel to Philosophy (Representation and Mind), Cambridge, MA: MIT Press.

Weingartner, P., and L. Schmetterer (eds.), 1987, Gödel Remembered: Salzburg 10–12 July 1983, (History of Logic, Number 4), Naples: Bibliopolis.

Wilkie, Alex, and J.B. Paris, 1987, “On the scheme of induction for bounded arithmetic formulas”, 35: 261–302.

Woodin, W. Hugh, 1988, “Supercompact Cardinals, Sets of Reals, and Weakly Homogeneous Trees”, Proceedings of the National Academy of Sciences of the U.S.A., 85(18): 6587–6591.

–––, 2001a, “The Continuum Hypothesis. I”, Notices of the American Mathematical Society, 48(6): 567–576.

–––, 2001b, “The Continuum Hypothesis. II”, Notices of the American Mathematical Society, 48(7): 681–690.

–––, 2002, “Correction: ‘The Continuum Hypothesis. II’”, Notices of the American Mathematical Society, 49(1): 46.

Yourgrau, Palle, 2005, A World Without Time. The Forgotten Legacy of Gödel and Einstein, New York: Basic Books.

Zach, Richard, 1999, “Completeness Before Post: Bernays, Hilbert, and the Development of Propositional Logic”, Bulletin of Symbolic Logic, 5(3): 331–366.