теории

Поделиться статьей в социальных сетях:

в избранное

Логика кондиционалов

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 18 сентября 2007 года.

В настоящей статье предлагается обзор недавних достижений в условной логике. Мы рассматриваем три основные традиции: первая из них работает с онтическими моделями, вторая сосредотачивается на вероятностных моделях, а третья задействует эпистемические модели кондиционалов.

Введение

Хотя условная логика интенсивно изучалась лишь в последние пятьдесят лет, эта область уходит корнями в античность и Средние века (начиная как минимум со стоицизма, как подробно объясняется в монографии Sanford 1989). Тем не менее все современные труды так или иначе ведут свое происхождение от наблюдения, высказанного Фрэнком Рамсеем в примечании к его статье «Общие пропозиции и причинность» (“General Propositions and Causality”, 1929; Рамсей 2003). Этот отрывок трактовался и перетолковывался (порой с противоположных точек зрения) многими исследователями с самого момента издания трудов Рамсея.

Исследование кондиционалов — довольно обширная область, из-за чего тщательный ее обзор представляется трудной задачей, однако по меньшей мере можно выделить первую волну современных работ, таких как Chisholm 1946, Goodman 1955, Rescher 1964 и др., которая длилась с конца 1940-х по начало 1960-х годов. Принято считать, что данная волна охватывает так называемые теории со-допустимости кондиционалов. Основная идея состоит в том, что кондиционал утверждаем, если из его антецедента наряду с подходящими (со-допустимыми) предпосылками вытекает его консеквент. В каком-то смысле работа над этими теориями предвосхитила дискуссии, которые начнутся в конце 1960-х годов. Собственно, при подобном подходе условия истинности кондиционалов можно оценить следующим образом: кондиционал является истинным, если существует вывод из антецедента и подходящих со-допустимых предпосылок к заключению кондиционала. А стало быть, такие теории нейтральны в отношении вопроса о том, обладают ли кондиционалы истинностными значениями. Теории со-допустимости предоставляют нам и теорию утверждаемости, и теорию истинности кондиционалов.

Так, разновидность анализа кондиционалов, представленная подходом Гудмена, обеспечивает для кондиционалов условия истинности в форме следующего теста: a > b истинно, если b вытекает согласно правилам из a наряду со множеством Γ истинных предложений c таким образом, что нельзя утверждать a > ¬ c. Данный подход проблематичен, если учесть, что в рамках него условия истинности кондиционалов производятся посредством условий истинности других кондиционалов. Из круга Гудмена нельзя выйти, не предоставив независимое описание Γ. В 1980-е предлагались изощренные описания подобного толка (см., напр., Kvart 1986). В связи с этим идеи Гудмена и других теоретиков со-допустимости в последние годы развивались исследователями, которые взялись за тщательный анализ каузальной и темпоральной структуры событий с тем, чтобы дать независимое описание гудменовского Γ. Однако данные теории в большинстве своем не внесли значительного вклада в дебаты о логике кондиционалов.

За десятилетний период (приблизительно с 1968 по 1978 годы) было выдвинуто три альтернативных логических подхода. В статье Сталнакера 1968 года (Stalnaker 1968) для кондиционалов применяется семантика возможных миров, а также предлагается система аксиом. Это в чистом виде теоретико-истинностный подход, который был затем поддержан влиятельной монографией Льюиса (Lewis 1973). Дэвид Льюис вдохновлялся той же онтической интерпретацией кондиционалов, которой руководствовался Сталнакер.

Адамса (Adams 1975) выдвигает совершенно иной подход. В нем формально рассматриваются представления о том, что вероятность (не вложенных) кондиционалов имеет вид соответствующей условной вероятности. Подход был изложен в статьях, которые предшествовали работе Сталнакера (Stalnaker 1968). Он сосредотачивается на (вероятностной) теории приемлемости, а не истинности, кондиционалов.

В статье Герденфорса (Gärdenfors 1978) предлагается третье направление исследований, главная идея которого состоит в том, чтобы предоставить условия приемлемости кондиционалов посредством (не-вероятностных) процедур по пересмотру убеждений. Данная традиция во многом была предвосхищена в работах Маки (Mackie 1962, 1972), а также их комментаторами (см., напр., Harper 1975, 1976; Levi 1977). Более того, работа Леви (Levi 1988) представляет собой важнейший очерк, дополняющий труды Герденфорса.

Большинство современных трудов по условной логике так или иначе относится к работе, выполненной в одной или нескольких из указанных традиций. Однако, разумеется, учитывая колоссальный объем работ в данной области, существуют также статьи или даже книги, которые не вполне вписывающиеся в обозначенные разделения или же их сочетания. Некоторые из них, к примеру, сосредоточены на (не-вероятностном) изучении индикативных кондиционалов; также стоит упомянуть важные труды, сочетающие темы случайности, времени и кондиционалов. Ряд замечаний и рекомендаций относительно дополнительных литературы на данную тему будет предоставлен в последнем разделе настоящего обзора.

Другим источником важных трудов по условной логике в последнее время стала информатика и теория вычислений. Часть из них связана с моделями каузальных кондиционалов, а другая относится к разработкам в области немонотонной логики. В силу ограничений объема мы не будем обсуждать здесь оба направления, однако оставим библиографические указания по первой теме и предоставим краткий обзор по второй теме, дополнив его сопоставлением с более типичными подходами в рамках философской логики.

Тест Рамсея и современные теории кондиционалов

Рамсей предлагает нам рассмотреть следующий сценарий. У человека есть пирожное, и он решает не есть его, поскольку в результате, по его мнению, у него заболит живот. Мы, с другой стороны, оцениваем его поведение и решаем, что он неправ.

Рамсей анализирует ситуацию так:Уверенность (belief), в соответствии с которой действует этот человек и которая состоит в том, что если он съест пирожное, то заболеет, берется, согласно представленному выше рассмотрению, как материальная импликация.

Мы не можем противоречить этой пропозиции ни до, ни после события, ибо она является истинной при условии, что человек не ел пирожное и до события у нас не было причины думать, что он его съест, а после события мы знаем, что он его не ел. Поскольку он не мыслил ничего ложного, почему же мы спорим с ним или осуждаем его?До события мы отличаемся от него вполне очевидным образом; дело не в том, что он верит в p, а мы в не-p, но в том, что он имеет отличную от нашей степень уверенности в q при условии p, и мы, очевидно, пытаемся склонить его к нашей точке зрения. Но после события мы оба знаем, что он не ел пирожное и что он не заболел.

Различие между нами в том, что он думает, что если бы он съел, то он бы заболел, тогда как мы считаем, что он бы не заболел. Но это prima facie не различие в степенях уверенности в какой-то пропозиции, ибо мы оба согласны относительно всех фактов. (Рамсей 2003: 193. — пер. измен.)В примечании 4 мы находим дополнительные разъяснения: Если два человека спорят «Если р, то будет ли q?» и оба сомневаются относительно р, они в качестве условия добавляют р к сумме своего знания и на этой основе спорят относительно q; так что в этом смысле «Если р, то q» и «Если р, то не-q» являются противоречивыми.

Мы можем сказать, что они фиксируют свои степени уверенности в q при условии р. Если р оказывается ложным, эти степени уверенности становятся пустыми. Если же какая-то из сторон уверена в не-р наверняка, вопрос перестает подразумевать для нее нечто еще, кроме вопроса относительно того, что следует из определенных законов или гипотез. (Рамсей 2003: 193. — пер. измен.)Данные фрагменты вдохновили немало последних теоретических трудов о природе кондиционалов и условиях их приемлемости или истинности. Сам Рамсей не считал, что кондиционалы являются носителями значений истинности. Тем не менее он полагал, что существуют рациональные условия, определяющие принятие или отвержение нами кондиционалов.

Примечание в статье Рамсея предоставляет нам рациональный способ проверки или тест, устанавливающий принятие или отвержение такого рода. И все-таки многие авторы отталкивались от идей Рамсея с тем, чтобы предложить условия истинности для кондиционалов. Вероятно, наиболее явный пример такого подхода представлен в статье Сталнакера (Stalnaker 1968)

От условий приемлемости к условиям истинности

Вот как Сталнакер подошел к идеям Рамсея в статье 1968 года:В соответствии с его решением, ваше рассуждение… должно состоять в простом мысленном эксперименте: добавьте антецедент (в качестве гипотезы) к сумме ваших знаний (или уверенностей), а затем проверьте истинность или ложность консеквента.

При таких условиях ваша уверенность в кондиционале должна равняться вашей гипотетической уверенности в консеквенте.Разумеется, Сталнакер прекрасно осознает, что такого рода процедура у Рамсея полностью определена лишь в случае, когда агент не имеет мнения относительно истинностного значения антецедента кондиционала, который находится в рассмотрении. И поэтому он задается вопросом: как придать процедуре, описанной Рамсеем, более общий характер? Сталнакер предлагает следующее решение:

Во-первых, добавьте антецедент (в качестве гипотезы) к сумме ваших уверенностей; во-вторых, внесите все корректировки, требуемые для поддержания общей согласованности (без того, чтобы при этом изменилась гипотетическая уверенность в антецеденте); наконец, проверьте итоговое значение истинности консеквента.

После того, как он сформулировал свою версию теста Рамсея, Сталнакер перешел от условий уверенности к условиям истинности, применив понятие «возможного мира»:Для того, чтобы совершить такой переход, нам требуется именно понятие возможного мира, поскольку возможный мир суть онтологический аналог суммы гипотетических уверенностей. Приведенный ниже набор условий истинности, в котором применяется данное понятие, является первым приближением к подходу, который я собираюсь предложить:Рассмотрим возможный мир, в котором a истинно и который в остальных аспектах минимально отличается от действительного мира. «Если a, то b» истинно (ложно) именно в том случае, когда b истинно (ложно) в таком возможном мире.

Анализ, обращающийся к возможным мирам, обладает также следующим преимуществом: он дает нам готовый понятийный аппарат, позволяющий построить семантическую теорию.Сталнакер предлагает переход от эпистемологии к метафизике, который основывается на использовании решающего понятия возможного мира. Ниже, однако, мы увидим, что предложенный им переход равносилен смене темы. Рамсей полагал, что кондиционалы не служат носителями истинностных значений, однако имеют точные условия приемлемости. К точному логическому и семантическому анализу также может привести интерпретация идей Рамсея, более верная им по духу и совместимая с представлением о том, что кондиционалы не выступают носителями значений истинности. Однако подобного рода кондиционалы имеют совершенно иные структурные свойства, в отличие от онтологических кондиционалов, рассматриваемых в тесте Сталнакера.Логике кондиционалов, выступающих носителями истинностных значений, посвящено немало исследований. В целях изучения подобных кондиционалов стандартный аппарат теории моделей можно расширить, включив в него техники, схожие с теми, что используются в модальной логике. В первом разделе настоящего обзора мы сосредоточим внимание на работах, принадлежащих данной традиции. Основная наша задача заключается в том, чтобы установить, какой именно семантический подход способен отразить параметры главных синтаксических систем, выдвигавшихся в научной литературе (включая слабые ненормальные системы, которые сыграли любопытную роль в ряде применений из информатики и теории вычислений).

Условия приемлемости: какого рода?

Существуют две основные традиции, ставящих себе целью обеспечение кондиционалов условиями приемлемости, а не истинности. Они отталкиваются от (расходящихся) интерпретаций исходного теста Рамсея. Одна из них опирается на выражение «степени уверенности» из примечания. Главная мысль состоит в том, что агенты «фиксируют свои степени уверенности в q при условии p», вводя последнее посредством классической байесовской кондиционализации. В общих чертах такой подход соответствует исследовательской программе, в рамках которой работают Эрнст Адамс (Adams 1965, 1966, 1975), ряд его учеников и целое множество последователей. Их цель состоит в разработке вероятностной семантики кондиционалов. Раздел 4 ниже посвящен рассмотрению данной разновидности семантики кондиционалов.

Согласно подходу Адамса, Макги и др., Рамсей предоставляет нам способ проверки приемлемости вероятностного толка, позволяющий вывести вероятность кондиционала в виде соответствующей условной вероятности. В статье Льюса (Lewis 1976) излагается хорошо известное опровержение допустимости данной идеи. Мы рассмотрим полученный Льюисом результат ниже, после чего обсудим его значение для исследователей, работающих в рамках данной традиции.

Существует также альтернативное направление исследований, начало которому было положено в статье Герденфорса (Gärdenfors 1978). В ней применяется теория приемлемости кондиционалов, не основанная на вероятности, и вместе с тем во многих важных отношениях она примыкает к программе Сталнакера и Льюиса, учитывающей онтологические соображения. Но, в отличие от Сталнакера, Герденфорс полагает, что тест Рамсея служит лишь способом проверки приемлемости, а вовсе не плацдармом для построения семантики возможных миров для кондиционалов.

Тест Рамсея

Герденфорс разработал семантическую теорию когнитивного толка, а затем применил ее для формализации идей Рамсея (Gärdenfors 1988). В пику большинству классических семантических теорий Герденфорс заявляет, что «предложение получает свое значение не из соответствия миру; нет, значение можно определить лишь в отношении к системе убеждений, или уверенностей (belief system)». Система убеждений, по Герденфорсу, образуется из следующих элементов: (1) класса моделей эпистемических состояний; (2) функции оценки, которая определяет эпистемические установки в состоянии для каждого эпистемического состояния; (3) класса эпистемических вводов (то есть входных данных); (4) функции принятия эпистемического обязательства *, которая для каждого состояния убеждения K и каждого эпистемического ввода a определяет новое суппозитивное (предположительное) состояние K*a.

Семантическая теория состоит в отображении структуры языка на систему убеждений. Если мы сосредоточимся на булевом языке L0, в котором нет модальных или эпистемических операторов, и допустим, что состояния уверенности моделируются дедуктивно замкнутым множеством предложений (множествами убеждений), тогда можно выделить три характеристики. Для любого предложения a ∈ L0 и множества убеждений K ∈ L0

a принимается в соответствии с K, если и только если a ∈ K.

a отвергается в соответствии с K, если и только если ¬a ∈ K.

a подвешивается в соответствии с K, если и только если a ∉ K, ¬a ∉ K.

Принятие — это важнейшая эпистемическая установка в семантической теории Герденфорса. Собственно, выражения обретают значение в L0 в силу критериев приемлемости, а не условий истинности. Тест Рамсея можно с легкостью использовать в контексте семантики Герденфорса, чтобы обеспечить критерии приемлемости предложениям вида «Если a, то b» (в записи «a > b»), выраженных в языке L> ⊇ L0. Разумеется, в этом случае нам необходимо будет обратиться к функции принятия эпистемического обязательства *. Для каждых a, b ∈ L0:

(Принять >)

a > b принимается в соответствии с K, если и только если b ∈ K*a.

При досистематическом рассмотрении кондиционалов как носителей истинностных значений вполне естественно было бы выразить принятие, как оно фигурирует в (Принять >), в виде уверенности в истинности соответствующего кондиционала. Более того, поскольку текущее множество убеждений K содержит все предложения, в которых агент полностью уверен, принятие «если a, то b» неизбежно отражается в его принадлежности K. Данную идею можно представить в виде условия редукции.

(УР)

a > b принимается в соответствии с K, если и только если a > b ∈ K.

Итак, (Принять >) можно переписать следующим образом:

(ГТР)

a > b ∈ K, если и только если b ∈ K*a.

(ГТР) в действительности представляет собой герденфорсовскую версию теста Рамсея. Разумеется, семантическая теория Герденфорса, взятая в сочетании с подходящими эпистемическими вариантами классических понятий выполнения, валидности и следования, окажется способной предоставить эпистемические модели условных операторов. (ГТР) в рамках такой теории будет служить «соединительной конструкцией», соотносящей (однозначным образом) свойства * со свойствами >.

В своей книге Герденфорс особенно концентрировался на изучении поведения таких эпистемических моделей в случаях, когда * следует ограничениям качественной версии кондиционализации, которую принято называть АГМ (см.: Gärdenfors 1988: ch. 1–5; Alchourrón, Gärdenfors, and Makinson 1985). Тем не менее, как показывает сам Герденфорс, лишь тривиальные модели удовлетворяют этим ограничениям. Собственно, Герденфорс доказал, что (ГТР) и три весьма интуитивных постулата смены убеждений под угрозой тривиальности оказываются противоречивыми. Этот результат сыграл в данной исследовательской программе роль, сходную с ролью льюисовского доказательства невозможности в рамках вероятностной исследовательской программы.

Ниже мы продемонстрируем, что (ГТР) вступает в разногласие с более слабыми ограничениями *, на необходимость которых однозначно указал Рамсей в своей формулировке «теста Рамсея». Тем самым мы докажем очень сильную разновидность так называемой теоремы невозможности Герденфорса.

(ГТР) предоставляет теорию принятия кондиционалов, которые при досистематическом рассмотрении оказываются носителями значений истинности и поэтому имеют мало общего с кондиционалами Рамсея. Герденфорс сам пришел к этому заключению в книге Gärdenfors 1988, хотя и не предоставил (ГТР) никакой альтернативы в целях дальнейшего развития семантической программы Рамсея. В следующем разделе мы представим возможную альтернативу.

Пересмотр теста Рамсея: более утонченная концепция принятия

К настоящему моменту читатель должен был убедиться: чтобы изложить идеи Рамсея должным образом, нам требуется гораздо более утонченная концепция принятия. Разумеется, в случаях пропозиций с истинностным значением в L0 различать принятие и полную уверенность не требуется. Однако нам также требуется концепция принятия, способная описать принятие предложений, которые не имеют значений истинности и при этом выражают важные когнитивные установки. Кондиционалы Рамсея представляют собой прекрасный пример таких предложений. Леви (Levi 1988) предлагает теорию принятия, отвечающую данным условиям.

Пусть L0 будет булевым языком, в состав которого не входят модальные и эпистемические операторы. Полные уверенности агента Х будут представлены множеством предложений L0, принятых X в определенный момент времени t. Это множество K предложений L0 должно быть замкнутым относительно логического следования.

С точки зрения X все составляющие K в момент t являются истинными. Они выступают основанием модальных суждений касательно серьезной возможности, которые, в свою очередь, не обладают истинностными значениями. К примеру, если a принимается в K, можно сказать, что ¬a не является серьезной возможностью с точки зрения X в момент t. Точно так же «если a, то b» служит оценкой серьезной возможности b, относящейся к преобразованию K (посредством добавления a), а не самому K. У таких эпистемических кондиционалов нет истинностных значений, и поэтому они «паразитируют» на K и его динамике. Принятие их не может быть формально отражено в их принадлежности K. Тем не менее отсюда еще не следует неспособность распознать производный (выразимый в расширенном языке L>) массив тех предложений L>, чья приемлемость зависит от приверженности K и обязательств агента по изменению в момент t.

Кондиционалы, принимаемые X в момент t, могут быть размещены во «вспомогательном множестве» s(K) ⊇ K. Леви вдобавок предлагает замкнуть s(K) относительно логического следования. Наконец, всякое предложение, принадлежащее s(K), также принадлежит K.

Теперь тест Рамсея можно выразить в следующем виде:

(ЛТР)

Если a, b ∈ L0, то a > b ∈ s(K) тогда и только тогда, когда b ∈ K*a, независимо от противоречивости или непротиворечивости K.

Возможность дополнения теста Рамсея его «отрицательной версией», способной разобраться с отрицаемыми кондиционалами, подробно исследовалась в рамках герденфорсианской традиции. Герденфорс и его коллеги (Gärdenfors et al. 1989) пришли к выводу, что при наличии очень слабых ограничений * (ГТР) нельзя дополнить отрицательной версией, имеющей вид:

(ОТР)

¬(a > b) ∈ K, если и только если b ∉ K*a.

Результат не кажется неожиданным. Обратите внимание на то, что из (ГТР) и (ОТР) следует, что a > b отвергается, если и только если a > b не принимается. Иными словами, агент X не может оставить кондиционал подвешенным. Данный результат, весьма контринтуитивный в случае кондиционалов, выступающих носителями истинностных значений, все же оказывается менее проблематичным (и, можно добавить, естественным) в отношении кондиционалов, у которых нет значений истинности. Поэтому вполне ожидаемо, что (ГТР) нельзя дополнить соответствующим (ОТР) из-за природы кондиционалов, рассматриваемых в тесте. Также не следует удивляться, что как только мы устраняем условие редукции, добавление следующей отрицательной версии (ГТР) не представляет совершенно никакой опасности:

(ЛОТР)

Если a, b ∈ L0, то ¬(a > b) ∈ s(K) тогда и только тогда, когда b ∉ K*a, независимо от противоречивости или непротиворечивости K.

Мы завершим данный очерк обзором логических систем, валидность которых подтверждается данными двумя тестами. Теорию также можно расширить, чтобы включить в нее условия приемлемости итерированных эпистемических кондиционалов. Когда язык-основа достаточно богат, чтобы включить в себя итерированные кондиционалы, а также булеву вложенность кондиционалов, возникает ряд новых условных систем, которые ранее не изучались в онтической традиции. Однако сначала мы обсудим основные логические системы, исследовавшиеся в онтической традиции, а также некоторые наиболее значимые проекты объединенной семантики (задействующей условия истинности).

Для начала рассмотрим набор важных правил вывода условной логики. Правила содержат символ, обозначающий материальную импликацию →, используемую в классической логике, а также символ ↔, который обозначает материальную двустороннюю импликацию (эквиваленцию). Они также содержат символ для конъюнкции в стандартном смысле.

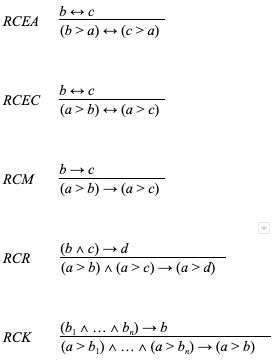
Переменная n должна быть больше или равна 0 в формулировке RCK. Условные логики, замкнутые относительно RCEA и RCK, называются нормальными. Условные логики, замкнутые относительно RCEA и RCEC, называются классическими. Условная логика, замкнутая относительно RCEA, называется монотонной или регулярной, если она замкнута относительно RCM или RCK. Наименования приведены по источнику Chellas 1980.

Правила RCEC и RCEA вводят очень слабое требование, согласно которому подстановки логически эквивалентных формул возможны соответственно в антецедентах и консеквентах кондиционалов. Хотя это лишь только имплицитно содержится в нотации, правила предполагают сохранение свойства теоремности, то есть мы подавляем появление синтаксического «турникета» (знака выводимости) как в антецедентах, так и в консеквентах.

Правило RCM в других контекстах (в немонотонной логике) называется «правым ослаблением» (‘Right Weakening’). Его идея заключается в том, чтобы разрешить выведение кондиционалов с логически более слабыми ограничениями из кондиционалов с тем же антецедентом и логически более сильными антецедентами. Мы выскажем несколько замечаний касательно регулярной и нормальной условных логик после того, как введем следующий перечень значимых аксиом.

PC  Любая аксиоматизация пропозиционального исчисления

ID a > a

MP (b > c) → (b → c)

CS (b ∧ c) → (b > c)

MOD (¬a > a) → (b > a)

CSO [(a > b) ∧ (b > a)] → [(a > c) ↔ (b > c)]

CC [(a > b) ∧ (a > c)] → (a > (b ∧ c))

RT (a > b) → (((a ∧ b) > c) → (a > c))

CV [(a > c) ∧ ¬(a > ¬b)] → ((a ∧ b) > c)

CMon [(a > c) ∧ (a > b)] → ((a ∧b) > c)

CEM (a > b) ∨ (a > ¬b)

CA [(a > c) ∧ (b > c)] → ((b ∨ a) > c)

CM (a > (b ∧ c)) → [(a > b) ∧ (a > c)]

CN (a > T)

Некоторые из этих аксиом достаточно спорны для ряда трактовок понятия кондиционала, а некоторые являются для него основополагающими. Пример вторых — аксиома ID, которая синтаксически выражает идею о том, что результат суппозиции какого-либо термина всегда успешен. Когда мы получаем новую информацию, нам не всегда требуется изменить взгляд для того, чтобы найти ей место. Один из возможных выходов в случае, когда новая информация нас крайне удивляет, состоит в приоритизации фоновой информации. Однако результат суппозиции термина предполагает, что рассматриваемая информация составляет часть суппозитивного сценария, созданного суппозицией термина.

В случае монотонных систем можно утверждать: система монотонна, если и только если она содержит CM и замкнута относительно RCEC. Есть два альтернативных способа описания регулярных систем, которые были введены выше сугубо через правила вывода при использовании аксиом. Условная система регулярна, если и только если она содержит CC и замкнута относительно RCM. Либо же система регулярна, если и только если она содержит CC и CM, а также замкнута относительно RCEC.

Аксиома CN интуитивно утверждает, что суппозитивный сценарий, открытый при предположении термина, всегда содержит все логические истины. Аксиома MP для modus ponens устанавливает связь между материальной импликацией (→) и более общей кондициональностью (>). Идея заключается в том, что всякий кондиционал влечет за собой соответствующую материальную импликацию. Большинство остальных аксиом будут разобраны в контексте конкретных логических систем.

Наименьшая классическая условная логика будет называться CE, а наименьшая нормальная условная логика — CK. Разумеется, имеются важные классические и ненормальные условные системы наподобие CEMN, которые, как мы увидим позже, могут быть использованы для выражения кондиционалов высокой вероятности. CE — очень слабая условная система, в которой отсутствует большая часть допущений по поводу кондициональности — даже тех, которые называются нами основополагающими для кондициональности, наподобие аксиомы ID. CK — даже будучи сильнее, чем CE, — тем не менее тоже представляет собой слабую систему (в которой аксиомы наподобие ID по-прежнему не принимаются).

В литературе исследовалась слабая система B, которая была предложена в Burgess 1981. Это наименьшая монотонная система, в состав которой входят ID, CC, CA и CSO. Если мы добавим CV в B, то получим систему V — слабейшую систему кондиционалов, которая была изучена в Lewis 1973. Хотя книга Льюиса посвящена контрфактическим системам, обзор системы V продиктован интересом к теме условной обязанности. Также выясняется, что система V, равно как и B, имеет интересные приложения в сфере искусственного интеллекта (так как они являются слабейшими условными системами, чьи невложенные фрагменты совпадают с хорошо известными системами немонотонной логики — мы разберем этот вопрос ниже). Специалисты по информатике и теории вычислений рассматривали также систему, которую Хэлперн называет AXcond (см. Halpern 2003). В ее состав входят аксиомы ID, CC, CA, CMon, и она замкнута относительно modus ponens RCEA и RCM. Далее мы убедимся, что она во многих важных аспектах связана с системой P немонотонной логики (см. раздел 4.4 ниже).

Многие философы, которые работают с онтическими кондиционалами в целом и контрфактическими высказываниями в частности, полагают, что MP требуется для моделирования этой разновидности кондиционалов, и некоторые из них также считают, что для этого требуется и CS. В число последних входят Поллок (Pollock 1981), который предложил систему SS, полученную при добавлении MP и CS в B, а также Дэвид Льюис, чья «официальная» аксиоматизация логики контрфактических высказываний представляет собой систему VC, полученную при добавлении MP и CS в V. Льюис все же рассматривает и более слабую систему VW, образованную путем добавления лишь MP в V. Другая значимая система — C2 Сталнакера, которая формируется из VC посредством замены CS на более сильное правило CEM (условное исключенное третье, conditional excluded middle). Лучше всего подобный выбор аксиом описывается через семантические соображения, которые будут представлены в последующих разделах.

Другая важная система, фигурировавшая в недавних дискуссиях на тему кондиционалов, была предложена в Delgrande 1987 — это система NP. Мы вернемся к ней в ходе (краткого) обзора связей с немонотонной логикой несколько позднее и опишем ее в семантическом ключе ниже.

Объединенная семантика классического семейства условных логик

Одна из наиболее известных семантик для кондиционалов может быть построена (в соответствии с идеями, впервые изложенными в Stalnaker 1968) при помощи функций выделения. Чтобы оценить кондиционал a > b в мире w, семантика использует функцию f:W×2W → W. Идея, легшая в основу семантики Сталнакера, была неформально представлена ранее:

 Рассмотрим возможный мир, в котором a истинно и который в остальных аспектах минимально отличается от действительного мира. «Если a, то b» истинно (ложно) именно в том случае, когда b истинно (ложно) в таком возможном мире.

 Таким образом, функция выделения f(w, |a|M) даст нам «ближайший» a-мир к w — где |a|M обозначает пропозицию, выраженную предложением a в модели M. Подобная семантика обобщается множеством способов. Один из них был выдвинут Льюисом, который предложил использовать функцию f:W×2W → 2W. Стало быть, в данном обобщении допускается существование различных a-миров, которые одинаково близки к w.

Однако это обобщение нельзя использовать для формирования объединенной семантики целого класса классических условных логик. Она все еще слишком сильна для описания таких систем, как B. В работе Burgess 1981 мы находим одну из первых попыток разработать единую семантику, охватывающую системы наподобие B.

Упорядочивающая семантика

Бёрджесс указал, что семантика, опирающаяся на функции выделения, не срабатывает для его системы B, и выдвинул альтернативу, которая основывалась на трехместных отношениях упорядочивания:

 Определение 1. Упорядочивающая модель представляет собой триплет M = ⟨W, R, P⟩, где W — непустое множество миров, R — тернарное отношение на W, а P — классическая функция оценки, которая приписывает пропозицию (множество миров) каждому атомарному предложению. Мы используем запись |a|M для обозначения множества истинности a, то есть множества миров в модели, в которой a истинно. Так, множества истинности кондиционалов задаются следующим образом:

Для x ∈ W мы устанавливаем Ix = {y : ∃z Rxyz ∨ Rxzy}. Тогда |a > b|M — множество всех миров x ∈ W таких, что ∀y ∈ (Iz ∩ |A|M) (∀z ∈ (Ix ∩ |A|M) ¬Rxzy) → y ∈ |B|M.

 Теперь укажем набор ограничений упорядочивающих моделей, которые окажутся полезными при дальнейшем обсуждении:

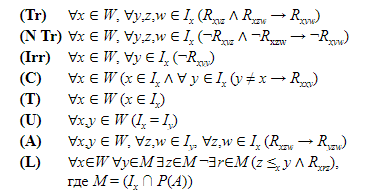
С помощью этих ограничений мы можем описать следующие важные системы:

 Теорема 1

(а) Множество упорядочивающих моделей, ограниченное (Tr), (Irr) и (L), является состоятельным и полным в отношении системы B.

(б) Множество упорядочивающих моделей, ограниченное (Tr), (Irr), (L) и (N Tr), является состоятельным и полным в отношении системы V.

(в) Множество упорядочивающих моделей, ограниченное (Tr), (Irr) и (N Tr), является состоятельным и полным в отношении системы NP.

Функции выделения множества

Второй проект по объединению был предложен Брайаном Челласом (Chellas 1980), который, в свою очередь, отталкивается от идей, впервые изложенных для одноместных модальностей Дэной Скоттом (Scott 1970) и Ричардом Монтегю (Montague 1970).

Идея состоит в получении функции, которая для данных пропозиции и мира выводит множество пропозиций вместо единичной пропозиции. Итоговое множество пропозиций может быть проинтерпретировано различными способами. К примеру, Челлас рассматривает их как необходимые пропозиции с учетом антецедента. А значит, записи a > b мы могли бы предпочесть запись [a]b. Или же рассматриваемые нами пропозиции могут быть пропозициями высоковероятного кондиционала с антецедентом a и т.д., и т.п. Мы будем использовать запись F(i, X), где X — пропозиция, i — мир референции, а F(i, X) — множество множеств миров. Назовем это функциями выделения множества, или функциями выделения окрестности.

Вслед за обозначениями Челласа можно ввести модель минимального кондиционала ⟨W, F, P⟩, где W — множество примитивных точек, F — функция F: W×2W → 22W, а P — оценка. Условия истинности такого кондиционала имеют вид

 (MC)

M, w ⊨ a > b, если и только если |b|M ∈ F(w, |a|M)

 Это не единственное возможное определение истинности при подобной настройке, однако именно его использует Челлас в книге по модальной логике. Одну из альтернатив можно представить следующим образом:

 (MC)

M, w ⊨ a > b, если и только если существует Z ∈ F(w, |a|M) и Z ∈ |b|M

 Два определения коэкстенсиональны до тех пор, пока кондициональные окрестности замкнуты относительно надмножеств (то есть монотонны). Однако в общем случае они не совпадают. Патрик Жирар (Girard 2006) отстаивает второе определение.

Система CE — наименьшая условная логика, замкнутая относительно правил RCEA и RCEC. CE задана всеми минимальными условными базисами. Система CM — наименьшая условная система, замкнутая относительно RCM. CM задана классом минимальных базисов, для которых выполняется следующее условие (где буквы Y, X и Z, а также их версии со штрихом обозначают пропозиции):

 (cm)

Если Y ∩ Y′ ∈ F(w, X), то Y ∈ F(w, X) и Y′ ∈ F(w, X)

CR — наименьшая условная логика, замкнутая относительно RCR. CR задается классом базисов, в котором выполняются и (cm), и условие вида

 (cc)

Если Y ∈ F(w, X) и Y′ ∈ F(w, X), то Y ∩ Y′ ∈ F(w, X)

 Логика, которая содержит классическую пропозициональную логику наряду с правилами RCEA и RCK, называется нормальной. Наименьшая нормальная условная логика — это система CK. CK задается классом базисов, удовлетворяющих (cm), (cc) и

 (cn)

W ∈ F(w, X)

 Очевидно, что мы можем располагать ограничениями или условиями, которые напрямую соответствуют перечню аксиом, изложенному в предыдущих разделах. К примеру, у нас есть

 (сa)

Если X ∈ F(w, Y) и X ∈ F(w, Z), то X ∈ F(w, Y ∪ Z)

(cso)

Если X ∈ F(w, Y) и Y ∈ F(w, X), то Z ∈ F(w, X) тогда и только тогда, когда Z ∈ F(w, Y)

(id)

X ∈ F(w, X)

Система B, выдвинутая Бёрджессом в любопытной статье Burgess 1981, описывается через условия (cc), (ca), (cso), (id) и (cm). Собственно, эта система содержит аксиомы ID, CC, CA, CSO и замкнута относительно правила RCM. Слабейшая условная система по иерархии Льюиса — система V — может быть получена при добавлении ограничения на функции выделения, соответствующего аксиоме CV:

 (cv)

Если X ∈ F(w, Y) и Zc ∉ F(w, Y), то X ∈ F(w, Y ∩ Z)

 Если мы вычтем условие (cm) из перечня условий, описывающего V, мы получим систему NP, впервые выдвинутую в работе Delgrande 1987.

Функция выделения класса F является пополненной тогда и только тогда, когда соблюдается следующее условие:

 Пополнение

X ∈ F(w, Y), если и только если ∩F(w, Y) ⊆ X.

 Для каждой пополненной функции выделения множества F можно задать обычную функцию выделения f, устанавливая f(w, X) = ∩F(w, X).

Сильные нормальные системы

Вероятно, основными нормальными системами являются системы C2 Сталнакера, VC Льюиса, SS Поллока и некоторые из более слабых по иерархии Льюиса условных систем, такие как VW. Интуитивно все эти системы представляются нам теориями минимального изменения, если воспользоваться терминологией из Cross and Nute 2001. Согласно такой точке зрения, кондиционал истинен просто в случае, если его консеквент истинен относительно каждого члена некоего выделенного множества миров, в котором истинен антецедент. Для того чтобы определить подходящее множество миров, где антецедент истинен, задействуется некоторое представление о минимальности. Поскольку мы обсуждаем онтические кондиционалы, как правило, минимизируется некоторое онтологическое понятие, такое как дистанция между действительным миром и множеством миров, где антецедент истинен.

Согласно Сталнакеру, всегда существует один и только один мир, более всего подобный действительному миру, где антецедент истинен. Потому получает поддержку сильное ограничение — так называемое условное исключенное третье. Льюис допускает существование множества миров, наиболее подобных действительному миру, и поэтому отвергает CEM, хотя и по-прежнему придерживается таких сильных аксиом, как CS и CV.

Семантика Льюиса лучше всего формулируется через системы моделей сфер. Мы представим такие модели в следующем же подразделе и затем сопоставим их с моделями, которые опираются на функции выделения.

Системы моделей сфер

Система модели сфер — это упорядоченный триплет M = ⟨W, $, P⟩, где W — это множество точек, P — функция оценки, а $ — функция, которая приписывает каждому i в W вложенное множество $i подмножеств W (сфер вокруг i). В соответствии с терминологией Cross and Nute (2001) для описания VC нам потребуются следующие ограничения систем моделей сфер:

 Центровка

{i} ∈ $i

SOS

i ∈ |a > b|, если и только если ∪$i ∩ |a| пусто или существует S ∈ $i такой, что S ∩ |a| не пусто и S ∩ |a| ⊆ |b|

 Сфера S ∈ $i будет называться a-разрешающей, если и только если ∪$i ∩ |a| ≠ ∅ (для краткости мы опустим соотнесенность каждой пропозиции с соответствующей моделью M). Так называемое граничное допущение (ГД) устанавливает, что если ∪$i ∩ |a| ≠ ∅, то существует наименьшая A-разрешающая сфера. Льюис выступил против граничного допущения как ограничения системы моделей сфер. Обратите внимание, однако, что его условия истинности не нуждаются в определении наименьшей a-разрешающей сферы для оценки a > b.

Какова связь между семантикой, опирающейся на системы моделей сфер, и семантикой, основанной на функциях выделения? В рамках подхода систем сфер мы всегда можем задать производную функцию выделения: пусть f(a, w) будет множеством a-миров, принадлежащих каждой a-разрешающей сфере в $i, если таковые существуют; если нет, речь идет о пустом множестве. Тогда, если мы используем стандартные условия истинности для функций выделения, условия истинности, определенные функциями выделения, которые были выведены из систем сфер, удовлетворяющих ГД, совпадают с условиями истинности, которые были определены для систем сфер. (По этой причине в работе Кросса и Ньюта (Cross and Nute 2001) теория кондиционалов Льюиса характеризуется как теория минимального изменения.) Но если функция выделения выведена из системы сфер, в которой не выполняется ГД, тогда два типа условий истинности расходятся (кондиционалы вида a > b такие, что функция f(a, w) пустая, будут обладать пустой истинностью в соответствии с семантикой функций выделения, однако этого не происходит в случае, когда семантика определяется через систему сфер).

Следует заметить, что Льюис все же придерживается граничного допущения в слабой его форме. Мы увидим это, если обратим внимание на то, что системе VC можно дать аксиоматизацию посредством аксиом ID, MP, MOD, CSO, CV и CS с RCEC и RCK в качестве правил вывода. Искомая нами аксиома — MOD, которая порождает следующее ограничение на функциях выделения:

 (mod)

Если f(a, w) = ∅, то f(b, w) ∩ |a| = ∅

 Даже если производная функция f подчиняется (mod), отсюда еще не следует, что в системе сфер, из которой она была выведена, выполняется граничное допущение. Ведь, разумеется, если f(b, w) ∩ |a| ≠ ∅, то a должна быть допустимой (entertainable), но не наоборот. И все же обратите внимание: согласно (mod), выполняется равенство f(a, w) ≠ ∅, когда a слабо допустима в том смысле, что f(b, w) ∩ |a| ≠ ∅. Вот каковы требования синтаксиса VC. Ниже я приведу перечень стандартных ограничений, которые окажутся полезными в дальнейшем:

 (L) Граничное допущение

∀a ∈ L ∀i ∈ W, если |a| ∩ ∪$i ≠ ∅, то существует наименьший член $i, который покрывает |a|.

(T) Полная рефлексивность

∀i ∈ W, i ∈ ∪$i

(A) Абсолютность

∀i, j ∈ W, $i = $j

(U) Единообразие

∀i, j ∈ W, ∪$i = ∪$j

(UT) Всеобщность

∀i ∈ W, ∪$i = W

Другие значимые нормальные системы

Поллок выдвигает аргументы против CV, вследствие чего его понятие минимальности отличается от льюисовского, хотя семантика Поллока по-прежнему представляет образчик теории минимального изменения. В одном из контрпримеров Поллока речь идет о двух лампочках L и L′, трех простых переключателях A, B, C и источнике питания. Элементы смонтированы так, что лампочка L загорается в точности тогда, когда замкнут переключатель A или же замкнуты переключатели B и C, в то время как L' загорается тогда, когда замкнут A или B. В момент начала обе лампочки не горят и все переключатели разомкнуты. То есть мы имеем

 (1) ¬(L′ > ¬L)

(2) ¬[(L′ ∧ L) > ¬(B ∧ C)]

 Обоснование первого кондиционала состоит в том, что приведение в действие L' подразумевает приведение в действие A, но истинно A > L; обоснование второго — загорание обеих лампочек требует замыкания и B, и C. Затем Поллок утверждает, что следующее контрфактическое высказывание также истинно:

 (3) L′ > ¬(B ∧ C)

 Его довод заключается в том, что L' требует лишь A или B, а приведение в действие C представляет собой неоправданное изменение, которое не следует допускать. Мнение Поллока не бесспорно. Вот как выступили против него Кросс и Ньют: 

 …это чрезмерно упрощенный подход. Задействованы не только A, B и C. Чтобы зажглась L', следует произвести также и другие изменения, например, заставить ток пройти на определенные расстояния в кабеле, где в данный момент он не проходит и т.д. Какой путь изберет ток, если L' горит? Вероятно, мы будем вынуждены выбирать между прохождением тока через определенный участок проволоки и замыканием переключателя C. Трудно сказать с уверенностью, какие опции имеются в нашем распоряжении при условии, что у нас нет диаграммы цепи, которую представляет себе Поллок. Но и без схемы проводки нелегко сказать, является ли замыкание C в случае (3), как утверждает Поллок, неоправданным. (Cross and Nute 2001)

 Другая трудность состоит в том, что этот пример описывает совершение действий, которые приводят к установлению определенного положения вещей, а такой язык нельзя должным образом отразить в графике цепи без оператора, который бы имел дело с соответствующими вмешательствами. Более значимая причина для отвержения CV заключается в нежелании работать с полным упорядочиванием миров, взятых в трактовке Льюиса и Сталнакера. Действительно, поллоковский анализ представления о подобии миров производит частичное, а не полное упорядочивание миров. Система Поллока SS — это собственное расширение системы B Бёрджесса, полученное путем добавления к его аксиоматике аксиом MP и CS.

Другая важная система — VW Льюиса. Если условия истинности даны через семантику сфер, условие центровки должно быть ослаблено: 

 Слабая центровка

Для каждого i ∈ W верно, что i принадлежит каждому непустому члену $i, причем существует по меньшей мере один такой член.

 Если, напротив, мы применяем производные функции выделения, то центровка выражается как

 f-центровка

Если i ∈ |a|, то f(a, i) = {i}.

А слабая центровка, в свою очередь, имеет вид

f-слабая центровка

Если i ∈ |a|, то i ∈ f(a, i).

 Подобное условие рационализируется двумя возможными способами. Либо мы прибегаем к «огрубленной» минимальной интерпретации —вокруг мира референции i имеется «ореол» миров, которые связаны в своем подобии i в соответствии с огрубленным понятием подобия. Либо мы изменяем интерпретацию функции выделения и заявляем, будто бы выделенные миры «достаточно» подобны миру референции, а не более всего подобны. Обе трактовки дают нам основание для принятия VW. 

Роберт Нозик (Nozick 1981) выдвигает независимые аргументы в пользу отвержения CS в своем знаменитом эссе о знании как «отслеживании истины». Большинство его примеров касаются стохастических ситуаций. Вот один из них: выпускается фотон, который пролетает через щель B (он мог пролететь через две щели, A и B). Отсюда не следует, что у нас есть основания утверждать: «Если фотон выпустить, он пройдет через щель B». Решение Нозика заключается в принятии VW как кодировки контрфактической логики.

Дональд Ньют (Nute 1980) соединил критику центровки (и дальнейшего принятия слабой центровки) с независимыми аргументами против CV. Он предлагает логику (назовем ее N), которая замкнута относительно всех правил и содержит все положения VW помимо CV. Разумеется, логика Поллока SS — это собственное расширение N.

Теории локального изменения

Говоря неформально, до сих пор мы рассматривали два вида трактовок функций выделения, используемые в анализе кондиционалов. С одной точки зрения, оценка a > b в i требует от нас удостовериться, является ли консеквент b истинным для класса a-миров, более всего подобных i. Согласно второй интерпретации функции выделения f(w, |a|M), функция выделяет множество миров, которые достаточно близки i. Мы также убедились, что VW занимает двойственное положение в иерархии условных систем. Она валидируется подходящим набором ограничений функций выделения, и эти ограничения могут быть рационализированы при каждой интерпретации функции выделения.

Существует третий способ интерпретации содержания функции выделения f(w, |a|M), а именно понять ее получение множества миров, которые в минимальных аспектах локально сходны с w, но вместе с тем могли бы отличаться от w в любой степени. Собственно, в той мере, в какой эти миры локально сходны с w, как нам требуется, они могут максимально отличаться от мира референции. 

Хрестоматийный пример теорий подобного толка приводится в Gabbay 1972. Упрощенная модель Габбая — это триплет M = ⟨W, g, P⟩, где первый и третий параметры ведут себя как в предыдущих моделях, а g — тернарный оператор, который приписывает предложениям a, b и миру i подмножество g(a, b, i) множества W. Кондиционал a > b истинен для i в такой модели, когда g(a, b, i) ⊆ |a → b|M, где «→» представляет материальную импликацию. Итак, вместо того, чтобы следовать более привычному паттерну подобия в оценке онтических кондиционалов, Габбай принимает совершенно иную установку касательно определения условий истинности подобных кондиционалов. Грубо говоря, его идея состоит в сохранении тех характеристик действительного мира, которые релевантны относительно эффекта, оказываемого a на истинность b.

Габбай накладывает ряд основных ограничений на тернарные функции выделения:

 (G1) i ∈ g(a, b, i)

(G2) Если |a| = |b| и |c| = |d|, то g(a, c, i) = g(b, d, i)

(G3) g(a, c, i) = g(a, ¬c, i) = g(¬a, c, i)

 С ними семантика Габбая определяет наименьшую условную логику, замкнутую относительно RCEC, RCEA и правила RCE, которое указывает, что из a → b следует выводить a > b (см. Nute 1980 и Butcher 1978, 1983). В соответствии с терминологией Cross and Nute 2001 мы называем эту логику G. Она является слабой, но не слабейшей среди рассматриваемых нами логик. До сих пор наименьшей среди затронутых систем была CE Челласа, которая представляет собой наименьшую условную логику, содержащую классическую пропозициональную логику и замкнутую относительно RCEA и RCEC.

Разумеется, можно предоставить G семантику, основанную на функции выделения окрестности. Нам требуется лишь добавить условие

 (rce)

Если |a| ⊆ |b|, то |b| ∈ F(i, |a|)

 Итак, G можно охарактеризовать через класс минимальных моделей, ограниченных (rce). Относительно того, как можно усилить G в рамках той разновидности семантики локального изменения, что используется Габбаем, ведутся дискуссии. К примеру, мы желаем добавить условия CC и CM. Один из способов это сделать заключается в наложении

 (G4) g(a, c, i) = g(c, a, i)

 Однако, как отмечается в статье Кросса и Ньюта (Cross and Nute 2001), тем самым мы уничтожаем наиболее характерную черту семантики Габбая. В работе Бутчера (Butcher 1978), однако, указывается, что CC и CM можно обеспечить посредством добавления более слабых, нежели (G4), условий. Разумеется, CC и CM можно параметрически и непроблематически ввести через добавление ограничений (cc) и (cm) к классу моделей окрестностей, ограниченных (rce). 

Другие семантики кондиционалов (в особенности тех кондиционалов, которые применяются в формулировке каузальных законов), следующие представлению о локальном изменении, изложенном в данном разделе, обсуждаются в работах Ньюта (Nute 1981) и Фетцера и Ньюта (Fetzer and Nute 1978, 1980).

Логика вероятностных кондиционалов

Существует множество разновидностей кондиционалов, относительно которых исследователи не пришли к единому мнению в вопросе о том, можно ли считать их носителями истинности. В некоторых случаях мы имеем положительные аргументы — наподобие выдвинутых в статье Гиббарда (Gibbard 1981): целый (грамматический или логический) класс кондиционалов не может обладать истинностными значениями (у Гиббарда речь идет об индикативных кондиционалах). Как мы можем предоставить для них семантику?

В начале данной статьи говорилось, что одним из вариантов здесь является развитие вероятностной семантики. Почему? Философская привлекательность вероятностной семантики объясняется не только мотивами, стоящими за тестом Рамсея для кондиционалов, — ее объяснение обнаруживается также в ряде пассажей из ранней статьи Сталнакера, посвященной вероятности и кондиционалам:

Эрнест Адамс (Adams 1975, 1965, 1966) предоставил базис для подобной оценки кондиционалов, и в последние годы ученые работали над улучшением данной теории (McGee 1994, Stalnaker and Jeffrey 1994). Прежде всего заслуживает внимания то обстоятельство, что большинство недавних исследований, посвященных вероятности и кондиционалам, а также часть ранних работ Адамса указывают в направлении, которое не согласуется с ожиданиями Сталнакера. Основная мысль указанного пассажа и остальной статьи Stalnaker 1970, равно как и последующих трудов, заключается в следующем: нужно задействовать нечто менее спорное, нежели сами кондиционалы, если мы хотим разрешить вопросы их семантики. Когда Сталнакер ссылается на «устоявшуюся математическую теорию», он, судя по всему, подразумевает аксиоматический подход Колмогорова, связывающий теорию вероятности с теорией меры.

По всей видимости, Сталнакер предполагает, что по меньшей мере это математическое ядро теории вероятности является фиксированным и благоприятственным в его применении к семантике кондиционалов. Тем не менее в недавних работах по вероятностной семантике кондиционалов исследователи отказываются от колмогоровской вероятности и сосредотачиваются вместо этого на доколмогоровских представлениях. Так, де Финетти изучал представление, в соответствии с которым аддитивная условная вероятность является примитивной и одноместная вероятность задается посредством нее. Сам Адамс пишет, скорее, об утверждаемости, нежели вероятности, оставляя нерешенным не только вопрос об интерпретации ее понятия, но и вопрос о ее математическом ядре.

Несмотря на то, что Сталнакера четко прописывает исходную мысль об исследовании кондиционалов с точки зрения зрелой теории вероятности колмогоровского толка, дальнейшие разработки увели это исследование в совершенно ином, более дискуссионном направлении. Как мы увидим далее, понятие вероятности, кажущееся подходящим для развития семантики кондиционалов, оказывается более схожим с идеей вероятности, распространенной в теории принятия решений, а также разделяемой Леонардом Сэвиджем и Бруно де Финетти (De Finetti 1990): речь идет о конечно аддитивной (примитивной) условной вероятности (в аксиоматизации Лестера Дабинса, см. Dubins 1975).

В данной области особую значимость имеет вывод Дэвида Льюиса (1976), который демонстрирует, что вероятность кондиционалов не является условной вероятностью. Прежде всего я представлю обзор основополагающих элементов аргументации Льюиса, а затем опишу семантический подход, который первоначально был разработан Адамсом, и его множество расширений, улучшений и заключений о возможности. Наконец, я перейду к анализу условных логик, получивших валидность через вероятностную семантику. 

Условная вероятность и вероятность кондиционалов

Следует представить главный парадокс (заключение о невозможности), первоначально изложенный в статье Льюиса 1976 года (Lewis 1976). Как это зачастую делается в данной области исследований, мы начинаем с функции вероятности, определенной над предложениями. На всем протяжении раздела 4 в соответствии с устоявшейся конвенцией мы будем обозначать предложения строчными буквами, а выражаемые ими пропозиции — заглавными. Итак, ‘a’ будет обозначать правильно построенную формулу, ‘A’ — множество точек в пространстве, где предложение ‘a’ истинно. Используемые пространство и модель будут проясняться в каждом конкретном случае. Это значительно упростит упростит запись. Следующие аксиомы описывают идею функцию вероятности: 

(1) 1 ≥ P(a) ≥ 0

(2) Если a и b эквивалентны, то P(a) = P(b)

(3) Если a и b несовместимы, то P(a ∨ b) = P(a) + P(b)

(4) Если a — теорема внутренней логики, P(a) = 1

Льюис далее сосредотачивается на классе таких функций вероятности, которые замкнуты относительно обусловливания. Когда P(b) положительна, существует такая P′, что P′(a) всегда равняется P(a | b), и Льюис утверждает, что P′ образуется из P через обусловливание на b. Класс функций вероятности замкнут относительно обусловливания, если и только если всякая функция вероятности, которая образуется через обусловливание из функции класса, сама принадлежит этому классу.

Теперь мы можем ввести несколько важных определений. Кондиционал > представляет собой кондиционал вероятности для P (или кондиционал всеобщей вероятности), если и только если > интерпретируется так, что для некоторой функции вероятности P и для любых предложений a и c

(CCCP)

P(a > c) = P(c | a), если P(a) положительно

‘CCCP’ означает кондициональное толкование условной вероятности (conditional construal of conditional probability). Терминология взята из Hájek and Hall 1994.

Теперь предположим для довода от обратного, что ‘>’ — кондиционал всеобщей вероятности. Обратите внимание, что если это верно, то мы получим

(5) P(a > c | b) = P(c | a ∧ b), если P(a ∧ b) положительно

Если ‘>’ — кондиционал вероятности для класса функций вероятности, и если класс замкнут относительно обусловливания, то (5) выполняется для каждой функции вероятности в классе и для всех a и c.

Теперь выделим любую функцию P, такую, что и P(a ∧ c), и P(a ∧ ¬c) положительны. Тогда P(a), P(c) и P(¬c) также положительны. По (CCCP) мы имеем P(a > c) = P(c | a). И по (5), подставляя b на место c или ¬c и упрощая правую сторону выражения, мы получаем следующее:

(6) P(a > c | c) = P(c | a ∧ c) = 1

(7) P(a > c|¬c) = P(c | a ∧ ¬c) = 0

Теперь, согласно теории вероятности, для каждого предложения d мы можем совершить разложение по случаям:

(8) P(d) = P(d | c) · P(c) + P(d|¬c) · P(¬c)

Подставив a > c вместо d и посредством очевидных замещений получаем

(9) P(c | a) = 1 · P(c) + 0 · P(¬c) = P(c)

Итак, мы пришли к заключению, что a и c независимы в вероятностном смысле относительно P, если и P(a ∧ c), и P(a ∧ ¬c) положительны, что представляет собой очевидный абсурд.

Расширения и заключения о возможности

Сам Льюис внес уточнения в результат (Lewis 1991), и в юбилейном сборнике статей, посвященном Эрнесту Адамсу (Eells and Skyrms 1994), был опубликован ряд расширений и доработок, к примеру, Hájek and Hall 1994.

Алан Хайек рассматривает несколько возможных ограничений (CCCP) и доказывает для них обобщенные формы льюисовской тривиальности. В частности, он рассматривает

Ограниченное CCCP

P(a > c) = P(c | a) для всех a, c в классе S.

Хайек затем приступает к обзору операций над функциями вероятности, которые называет пертурбациями. Эти операции охватывают и другие интересные операции — в том числе обусловливание и обусловливание Джеффри. Предположим, у нас есть функция P, а также предложения a и b такие, что мы получаем

Совпадение

P(a > c) = P(c | a).

Затем допустим, что другая функция P' приписывает иную вероятность кондиционалу:

(1) P′(a > c) ≠ P(a > c)

Теперь, если P' приписывает ту же условную вероятность, что и P:

(2) P′(c | a) = P(c | a)

Мы немедленно приходим к

(3) P′(a > c) ≠ P′(c | a)

И точно так же, если P и P' сходятся в вероятности кондиционала, но расходятся в условной вероятности, их нельзя приравнять друг к другу. По крайней мере, не для такого выбора a и c. По словам Хайека, такие пары функций вероятности легко обнаружимы.

Я покажу, что существуют значимые способы соотнесения P и P', которые приводят к отрицательному результату для [ограниченного CCCP].

В самом деле, Хайек доказывает, что если P' представляет пертурбацию P относительно данного ‘>’, тогда не более чем одна функция из P и P' является CCCP-функцией для ‘>’ (см. Hájek 1994).

Тем не менее ван Фраассен (van Fraassen 1976) продемонстрировал, что ограниченное CCCP выполняется для некоторых подходящих пар антецедентных и консеквентных пропозиций a и c. Эрнест Адамс и Ван Макги рассматривают следующее особое сильное синтаксическое ограничение CCCP:

Исходная гипотеза Адамса (ИГА)

P(a > c) = P(a ∧ c)/P(a)

если P(a) ≠ 0

P(a > c) = 1

в иных случаях

где и a, и c являются фактическими (свободными от кондиционалов) предложениями (McGee 1994: 189)

Если трактовать кондиционал (вслед за стоиками) как замаскированное следование и не считать, что кондиционалы обладают истинностными значениями или что их интерпретация в некотором объективном смысле зафиксирована за множеством субъектов верований, исходная гипотеза Адамса представляется вполне оправданной — по крайней мере, за исключением предельного случая P(a) = 0, как будет указано ниже.

Дэвид Льюис во многих отношениях подходит к вопросу иначе. Прежде всего он считает итерации кондиционалов адекватными — и он ищет интерпретацию кондиционала, зафиксированную относительно разных субъектов верований:

Даже если существует кондиционал вероятности для всякой функции вероятности в классе, отсюда еще не следует, что имеется кондиционал вероятности для всего класса. Разные члены класса могут потребовать различных интерпретаций >, чтобы вероятности кондиционалов и условные вероятности совпали. Но наш индикативный кондиционал предположительно имеет фиксированную интерпретацию, одинаковую для носителей различных убеждений и для одного из носителей до и после смены его убеждений. А иначе как могут возникать разногласия или происходить перемены во мнениях относительно кондиционала? (Lewis 1976)

Льюис был убежден, что интерпретация кондиционала, не зависящая от убеждений высказывающего его лица, не поддерживается его теорией. Это легко увидеть, если обратить внимание, что кондиционалы и их семантика могут обладать «скрытой индексальностью». Как правило, считалось, что аргумент ван Фраассена предоставляет вероятностную семантику для кондиционалов, понятых как индексальные выражения, основанные на убеждениях высказывающих их лиц. Чем больше мы разделяем эпистемическое представление о кондиционалах, тем больше их интерпретация будет опираться на текущие убеждения (причем необязательно с помощью отсылки к скрытой индексальности).

В контексте данной статьи исходная гипотеза Адамса послужит хорошей отправной точкой. В дальнейших разделах мы увидим, что исходный его тезис также сталкивается с внутренними трудностями, не зависящими от проблем, вытекающих из парадоксов Льюиса и их продолжений.

Исходная гипотеза Адамса и связанные с ней трудности

Чтобы оценить некоторые из проблем, связанных с ИГА, нам следует для начала отделить друг от друга два вероятностных критерия валидности, о которых писал Макги (McGee 1994):

Вероятностная валидность

Вывод вероятностно валиден, если и только если для каждого положительного ε существует положительное δ такое, что при любом приписывании вероятности, в рамках которого каждая из посылок будет вероятна более, чем 1−δ, заключение будет иметь вероятность по меньшей мере 1−ε.

Вдобавок существует альтернативный критерий валидности, который, судя по всему, даже более интуитивен:

Строгая валидность

Вывод строго валиден, если и только если заключение имеет вероятность 1 при любом приписывании вероятности, в рамках которого вероятность каждой из посылок равна 1.

Ван Макги предлагает тонкий анализ того, как ведет себя ИГА при использовании ее в сочетании с этими критериями. Основная проблема здесь состоит в том, что наша теория английских кондиционалов при использовании критерия вероятностной валидности оказывается крайне скупой: к примеру, транзитивность, контрапозиция и прочие правила вывода в этом случае не работают. Однако:

Строго валидные выводы описываются не теорией Адамса, а обычной теорией, в которой английский кондиционал трактуется как материальная импликация. 

Это вызывает нехорошее подозрение. Классические валидные способы вывода терпят неудачу лишь тогда, когда мы из посылок, менее чем достоверных (то есть их вероятность менее 1), приходим к заключению, которое также менее чем достоверно. Как только посылки оказываются для нас достоверными, можно с уверенностью вывести классически разрешимые следствия…

При установлении того, что строго валидные выводы являются классическими, наиболее важную роль играет не главный тезис Адамса, а… состояние по умолчанию, приписывающее вероятность 1, когда условная вероятность не определена. Состояние по умолчанию никак не отражает английский узус, да и не должно его отражать… Напротив, как замечает Адамс, состояние по умолчанию лишь «произвольно постулировано» в качестве меры по устранению особого случая, который максимально удален от главного предмета наших интересов. И тем не менее это состояние причинило немало ущерба, так что нам пора отыскать ему замену. (McGee 1994) 

И замена эта, по словам Макги, находится прямо под рукой. Нам нужно обратить внимание на исходное представление об условной вероятности, которое имелось у нас уже давно в различных исторических вариантах. Макги сосредотачивается на одной из таких версий, а именно — на условной вероятности в аксиоматизации Карла Поппера (Поппер 2005: приложения). Функция Поппера над языком L для классического исчисления высказываний — это функция P: L×L → R, где R обозначает вещественные числа, которая подчиняется следующим аксиомам:

1. Для любых a и b существуют c и d такие, что P(a | b) ≠ P(c | d)

2. Если P(a | c) = P(b | c) для каждого c, то P(d | a) = P(d | b) для всех d

3. P(a | a) = P(b | b)

4. P(a ∧ b | c) ≤ P(a | c)

5. P(a ∧ b | c) = P(a | b ∧ c)·P(b | c)

6. P(a | b) + P(¬a | b) = P(b | b), если не P(b | b) = P(c | b) для любого c

Аксиома (5) крайне важна — и куда старше своего применения в теории Поппера. Она уходит корнями по меньшей мере в труды Джеффриса, где, в свою очередь, она была представлена как правило произведения У.Э. Джонсона (см. Jeffreys 1961: 25). В наши дни оно называется также аксиомой умножения.

С помощью такого представления об условной вероятности мы теперь можем установить новую форму гипотезы Адамса:

Улучшенная гипотеза Адамса

P(a > c) = P(c | a), где и a, и c — фактические (свободные от кондиционалов) предложения.

Посредством гипотезы Адамса в новой формулировке Макги показывает (см. McGee 1994: theorem 3), что вероятностная валидность и строгая валидность совпадают, как и должны. Это лишь один из признаков того, что верная формулировка гипотезы Адамса требует обращения вовсе не к классическому представлению об условной вероятности, которое было выражено в аксиомах Колмогорова, а к аксиоматизации ее посредством правила произведения Джонсона (далее просто правила произведения) и других подходящих аксиом.

Условная вероятность: две традиции

В теории условной вероятности имеются как минимум две основные традиции, которые способны работать с событиями обусловливания нулевой меры. Одна представлена принципом условной согласованности Дабинса (Dubins 1975): для всех пар событий A и B таких, что A ∩ B ≠ ∅:

(1) Q(.) = P(. | A) — конечная аддитивная вероятность,

(2) Q(A) = 1,

(3) Q(. | B) = Q[B](.) = P(. | A ∩ B)

Когда P(A ∩ B) > 0, условная согласованность отражает некоторые аспекты идеи де Финетти об условной вероятности при данном событии, а не при данном σ-поле. 

Небезызвестная колмогоровская альтернатива первому представлению действует следующим образом. Пусть ⟨Ω, B,P⟩ — это пространство с мерой, где Ω — множество точек, B — σ-поле множеств подмножеств Ω с точками w (множество B замкнуто относительно дополнения и счетного объединения его членов). Если P(A) > 0, A ∈ B, условная вероятность над B при A определяется так: P(. | A) = P(. ∩ A)/P(A). Разумеется, это не дает нам указаний, если P(A) = 0. Зато общепринятое представление применяет следующую стратегию. Пусть A будет под-σ-полем B. Тогда P(. | A) — это равномерное условное распределение (РУР) B при данном A, если верно, что

(4) Для любого w ∈ Ω, P(. | A)(w) — вероятность на B

(5) Для любого B ∈ B, P(B|A)(.) — A-измеримая функция 

(6) Для любого A ∈ A, P(A ∩ B) = ∫A P(B|A)(w) dP(w)

Колмогоров показывает с помощью своей версии парадокса Бореля, что P(. | A) — это вероятность не при данном событии, но при σ-поле. Блэквелл и Дабинс обсуждают условия собственности для РУР (Dubins 1975). Равномерное условное распределение P(. | A)(w) на B при A является собственным в w, если P(. | A)(w) = 1, всякий раз, когда w ∈ A ∈ A. В иных случаях P(. | A)(w) является несобственным. Недавние исследования показали, что когда B порождается счетно, почти наверное в отношении P, РУР на B при A оказываются максимально несобственными (Seidenfeld, Schervish, and Kadane 2006). Это верно в двух смыслах. С одной стороны, множество точек, где не выполняется собственность, имеет меру 1 при P. С другой стороны, мы получаем P(a(w)|A)(w) = 0, когда для собственности требуется P(a(w)|A)(w) = 1.

Представляется, будто бы провалы собственности никак не стыкуются с каким бы то ни было приемлемым эпистемологическим истолкованием той разновидности вероятности, которая широко применяется во многих направлениях математической экономики, философии и информатики. Разумеется, конечно аддитивная вероятность, подчиняющаяся принципу условной согласованности, несвободна от проблем оснований, однако, в соответствии со второй строкой принципа, каждая согласованная конечно аддитивная вероятность является собственной. Вдобавок, Дабинс (Dubins 1975) показывает, что каждая безусловная конечно аддитивная вероятность обладает полным множеством согласованных условных вероятностей.

В данном разделе я буду рассматривать лишь собственные вероятности. Я начну с обсуждения принципа условной согласованности и добавлю аксиому счетной аддитивности лишь к ограниченным применениям, где область Ω, будучи бесконечной, является счетной. Затем я определю качественную уверенность исходя из условной вероятности, прибегнув к процедуре, изученной в работах van Fraassen 1976, Arló-Costa 2001 и Arló-Costa and Parikh 2005. Обратите внимание, что аксиоматизация, предложенная Поппером и применяемая Макги, также имеет дело с конечно аддитивной вероятностью. Различие между конечно аддитивной вероятностью и счетно аддитивной вероятностью играет важную роль в языках, которые достаточно выразительны для его установления. Мы проясним это ниже при введении языков с бесконечным, но счетным количеством атомарных пропозиций. 

Макги представляет аксиомы Поппера как «естественное обобщение обычного представления об условной вероятности, в терминах которого сингулярности, возникающие на краю достоверности в других случаях, более не возникают» (McGee 1994: 190). Под таким представлением он подразумевает, судя по всему, определение через обычное соотношение. И Макги имеет в виду ту разновидность определения, которая берет за основу понятие одноместной вероятности, являющейся в себе конечно аддитивной. Однако это не обычное представление об условной вероятности, которое можно вывести из трудов Колмогорова. Подобное представление опирается на понятие одноместной вероятности, для которого важнейшей аксиомой выступает счетная аддитивность (она требует, чтобы сумма вероятностей P(Xi) счетного семейства событий Xi с объединением X равнялась P(X)). До тех пор, пока область, над которой определяется вероятность, является бесконечной (и остальные части статьи Макги — касающиеся бесконечно малой вероятности — по всей видимости, указывают на его интерес к бесконечным областям), конечно аддитивное понятие условной вероятности, предлагаемое им, выступает расширением не классической колмогоровской концепции, а конечно аддитивной одноместной вероятности. Итоговое представление конечно аддитивной условной вероятности — это доколмогоровское понятие вероятности, аксиоматизированное Дабинсом.

Наша первая аксиома предоставит нам как ресурсы для отслеживания противоречивости, так и совместимое с условной согласованностью интуитивное ограничение условной вероятности:

(I) Для любого фиксированного A функция P(X | A) в качестве функции от X либо выступает мерой (конечно аддитивной) вероятности, либо имеет постоянное значение 1.

(II) P(B ∩ C | A) = P(B | A)P(C | B ∩ A) для всех A, B, C в F.

Вероятность (simpliciter) A — pr(A) — представляет собой P(A | U). Как можно увидеть, аксиома (II) соответствует правилу произведения (или аксиоме умножения), упомянутому ранее. Поскольку мы имеем дело с событиями, аксиомы оказываются более простыми, нежели в изложении аксиом Поппера (которые приписывают вероятности предложениям, а не событиям).

Если P(X | A) — вероятностная мера как функция от X, то A нормально, в противном случае A абнормально. Обусловливание с абнормальными событиями помещает агента в состояние несогласованности, представленное функцией с постоянным значением 1. Таким образом, A нормально, если и только если P(∅|A) = 0. Van Fraassen 1976 показывает, что надмножества нормальных множеств нормальны и что подмножества абнормальных множеств абнормальны. Если допустить, что полное пространство нормально, абнормальные множества имеют меру 0, хотя обратное не выполняется. В дальнейшем мы будем рассматривать случаи, при которых U нормально.

Теперь можно ввести понятие ядра вероятности. Ядро — множество K, которое нормально и удовлетворяет сильному условию превосходства (SSC): если A — непустое подмножество K, а B не пересекается с K, то P(B | A ∪ B) = 0 (и поэтому P(A | A ∪ B) = 1). Следовательно, любое непустое подмножество K вызывает большую «уверенность», нежели любое множество, не пересекающееся с K. В таком случае мы можем установить, что все непустые подмножества ядра нормальны.

Когда универсум точек не более чем счетен, проявляются изящные свойства ядер и условных мер, которые могут быть использованы для определения полной уверенности и ожидания без парадоксов. 

Лемма 1 (Нисходящие цепи) (Arló-Costa 1999). Когда универсум точек не более чем счетен, цепь ядер убеждений, вызванная счетно аддитивной условной функцией P, не может содержать бесконечно нисходящую цепь ядер.

В общем случае можно продемонстрировать, что для каждой функции P существуют как наименьшее, так и наибольшее ядро, и что наименьшее имеет меру 1. К тому же, когда универсум счетен, мы можем добавить счетную аддитивность, не нарушая собственности. В этом случае получается, что наименьшее ядро образуется именно теми точками, которые обладают положительной вероятностью. Все ядра имеют вероятность 1, но, разумеется, лишь у самых глубоких ядер нет подмножеств с нулевой мерой. Вдобавок существует поразительное различие между наибольшим и наименьшим ядрами (а также между наибольшим и любым другим). В самом деле, любое множество S, содержащее наибольшее ядро, устойчиво в отношении к суппозициям, а именно: P(S | X) = 1 для всех X, и дополнение S абнормально. Так что наибольшее ядро кодирует сильное доксическое понятие достоверности, или полной уверенности, тогда как наименьшее — более слабое понятие «почти достоверности», или ожидания. Итак, когда универсум счетен и выполняется счетная аддитивность, можно определить две основные установки: Событие ожидается, если оно содержит наименьшее ядро, и в нем полностью уверены, если оно содержит наибольшее ядро.

В общем случае имеется достаточно структур для определения обеих установок. Собственно, в такой ситуации существование глубочайшего ядра не может быть гарантировано. Но определение полной уверенности не нуждается в преобразовании, а понятие ожидания можно описать так: Событие ожидается, если оно подразумевается каким-либо ядром.

Логика предпочтений и рациональная логика: модель КЛМ

Понятие счетной ядерной логики, которое было выведено из вероятностной семантики и представлено в предыдущем разделе, имеет много важных точкек соприкосновениями с логикой предпочтений и рациональной логиками, введенными в работе Крауса, Леманна и Магидора (Kraus, Lehmann and Magidor 1990). Эти логики описывают представление о немонотонном следовании, а не кондиционалах, однако ниже мы увидим, что существуют любопытные и немаловажные пересечения между невложенной условной логикой и логикой предпочтений.

Определение 2. Если P ⊆ S и ‘<’ — это бинарное отношение на S, P — это гладкое подмножество S тогда и только тогда, когда ∀t ∈ P, либо существует s, минимальное в P, такое что s < t, или t само минимально в P.

Определение 3. Модель предпочтений M для универсума U — это триплет ⟨S, l, < ⟩, где S — множество, элементы которого будут называться состояниями, l: S → U — функция разметки, которая приписывает мир из универсума референции U каждому состоянию, а ‘<’ — это строгая частичная упорядоченность на S (то есть нерефлексивное, транзитивное отношение), которая удовлетворяет следующему условию гладкости: для всех a, принадлежащих пропозициональному языку-основе L, множество всех состояний â = {s : s ∈ S, s ⫢ a} гладкое; где s ⫢ a (читается как «s удовлетворяет a»), если и только если l(s) ⊨ a, где ‘⊨’ — это классическое логическое следование («влечет»).

Введенные выше определения позволяют преобразовать классические понятия следования (entailment) и истины в манере, схожей с идеями семантики, исследованными в разделе 3. Следующее определение показывает, как это можно сделать:

Определение 4. Даны модель M = ⟨S, l, <⟩ и a, b ∈ L. Отношение следования (entailment), заданное M, будет обозначаться как M и определяться в виде: a M b, если и только если для всех s, минимальных в â, s ⫢ b.

Модели предпочтений использовались в Kraus, Lehmann and Magidor 1990 для установления семейства логик предпочтения. В Lehmann and Magidor 1988 упор делался на подсемействе моделей предпочтения — так называемых ранжированных моделей.

Определение 5. Ранжированная модель R — это модель предпочтений ⟨S, l, <⟩, где строгая частичная упорядоченность < задается следующим образом: существует вполне упорядоченное множество W (строгая упорядоченность на W будет обозначаться ∠) и функция r: S → W такие, что s < t, если и только если r(s) ∠ r(t).

Действие функции r состоит в ранжировании состояний; так, состояние меньшего ранга более нормально, чем состояние высокого ранга. Здесь интуиция заключается в том, что для r(s) = r(t) состояния s и t находятся на одном уровне во внутреннем упорядочивании. Ранжирование станет более понятным, если обратить внимание, что > выступает частичной упорядоченностью на множестве T и условие ранжирования, которое было представлено выше, эквивалентно следующему свойству:

(Отрицательная транзитивность)

Для любых s, t, u в T таких, что s < t, верно либо u < t, либо s < u.

Леманн и Магидор помимо прочего ввели ранжированные модели, где упорядочивание не нуждается в выполнении требования гладкости.

Определение 6. Грубо ранжированная модель V — это модель предпочтений ⟨S, l, <⟩, для которой ранжируется строгая частичная упорядоченность < и опущеное требование гладкости.

С точки зрения синтаксиса, Краус, Леман и Магидор доказали теорию репрезентации в терминах приведенных выше моделей предпочтений для следующей системы P:

LLE обозначает «левую логическую эквивалентность» (left logical equivalence), RW — «правое ослабление» (right weakening) и CM — «осторожную монотонность» (cautious monotony). Леман и Магидор доказали, что система R, полная в отношении ранжированных моделей, может быть получена путем добавления к данному набору правил следующего правила рациональной монотонности:

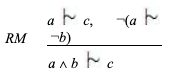
Естественным образом получается, что если добавляется RM, то более не необходимо CM. В статье Леманна и Магидора (Lehmann and Magidor 1988) предполагается, что синтаксическая система RR, полученная из R путем устранения правила CM, является состоятельной и полной в отношении грубо ранжированных моделей. Они выводят эту гипотезу из трудов Джеймса Делгранда по условной логике.

Легко заметить сходство между правилами, представленными в этом разделе, и условными аксиомами и правилами, обсуждавшимися ранее. К примеру, R соответствует аксиоме ID, RM — аксиоме CV и т.д., и т.п. Возникает вопрос: какова логическая связь между рациональными логиками и логиками предпочтениями, с одной стороны, и подходящими невложенными фрагментами условных систем, рассмотренных нами ранее, с другой. Данный вопрос будет затронут в разделе 4.6.

4.5 Счетная ядерная логика и вероятностные модели

S = ⟨U, F⟩ — вероятностное пространство, где U счетен и F является булевой подалгеброй множества всех подмножеств U. Нельзя обойтись без допущения относительно размера U; на протяжении всего раздела мы будем прибегать к нему в версии Arló-Costa and Parikh 2005.

Определение 7. M = ⟨S, P, V⟩ — это вероятностная модель, если S = ⟨U, F⟩ — вероятностное пространство, U — счетное множество, а F — булева подалгебра множества всех подмножеств U. V — это классическая оценка, отображающая все атомарные предложения L в измеряемые события на F, а P — это двухместная функция на U, для которой выполняются условия:

(I) для каждого фиксированного A функция P(X | A) в качестве функции от X выступает мерой (конечно аддитивной) вероятности или имеет постоянное значение 1.

(II) P(B ∩ C | A) = P(B | A) · P(C | B ∩ A) для всех A, B, C в F.

Мы используем буквы A, B и др. для обозначения событий в F.

Определение 8. Вероятностная модель счетно аддитивна, если и только если для каждого фиксированного A функция P(X | A) в качестве функции от X выступает мерой счетно аддитивной вероятности или имеет постоянное значение 1.

Пусть упорядочивание < на U будет определено для всех (отдельных) пар точек p, q таких, что {p, q} нормально при условии: p < q, если и только если P({p}|{p, q}) = 1; то есть если мы знаем, что мы выбрали одну из p, q, то это должна быть p. Точно так же, пусть p ≅ q, если и только если 0 < P({p}|{p, q}) < 1. Теперь мы можем назвать упорядочивание <, произведенное вероятностной моделью M, ранжирующим упорядочиванием для M. Обратите внимание на королларий леммы нисходящих цепей:

Лемма 2. Ранжирующее упорядочивание < для счетно аддитивной вероятностной модели M вполне фундированно.

Теперь мы можем установить: a < M b, если и только если для каждого u ∈ U такого, что u минимально в A, в соответствии с ранжирующим упорядочиванием для M, u ∈ B. Важно отметить, что есть также альтернативное вероятностное определение. Согласно ему, a PM b, если и только если P(B | A) = 1. Эти два способа определения надклассического отношения следования тесно связаны друг с другом, однако ниже мы установим, что они совпадают не во всех случаях.

С этого момента важно проводить четкие различения касаемо природы языка-основы L, используемого для определения немонотонных отношений. Если множество примитивных пропозициональных переменных, задействованных в определении L, является конечным, то язык можно назвать логически конечным. В таком случае мы можем установить следующий результат:

Теорема 2. Если язык-основа логически конечен, то при условии, что a R b, существует счетно аддитивная вероятностная модель M такая, что a < M b.

Когда L счетно, ситуация становится несколько более сложной. В этом случае R более не полна в отношении счетно аддитивных вероятностных моделей. Такой исход прекрасно демонстрирует следующая лемма (опирающаяся на технику, задействованную в лемме 1 из Lehmann and Magidor 1988):

Лемма 3. Когда L счетно, существует рациональное отношение, которое задается не счетно аддитивной вероятностной моделью.

Эта лемма весьма важна для нашего изложения. Она показывает, что даже если мы ограничиваемся бесконечными, но счетными вероятностными областями и даже если язык обладает достаточной выразительностью, счетная аддитивность не может быть добавлена в качестве ограничения на вероятностные модели, поскольку в противном случае мы окажемся неспособны прийти к описанию интересующего нас рационального отношения. В контексте тесной связи между условными логиками и немонотонными отношениями следования это означает, что интересующее нас понятие вероятности точно не выводимо из трудов Колмогорова — речь идет о доколмогоровской конечно аддитивной вероятности.

Отсюда следует естественное предложение рассмотреть вероятностные модели, где необязательно требуется счетная аддитивность. Мы можем назвать такие модели конечно аддитивными.

Лемма 4. Если язык-основа содержит многие счетные буквы пропозиций, то существует конечно аддитивная вероятностная модель M такая, что a PM b, если a R b.

Нетрудно увидеть, что a PM b также состоятельно в отношении a R b. Тем не менее, a < M b оказывается несостоятельным в отношении a R b. Все нижеследующие результаты опираются на допущение, что язык-основа счетен.

Лемма 5. Когда M конечно аддитивна, < M оказывается несостоятельным в отношении R.

Тем не менее состоятельность выполняется в отношении системы RR, введенной в Lehmann and Magidor 1988.

Лемма 6. Когда M — это конечно аддитивная вероятностная модель, < M состоятельно в отношении RR.

Определение 9. Вероятностная модель M = ⟨S, P,V ⟩ является гладкой, если и только если для каждого предложения α соответствующее ему событие в модели является гладким в отношении ранжирующего упорядочивания, произведенного P.

Теперь ясно, что отношение PM, удовлетворительное во всех конечно аддитивных вероятностных моделях, тождественно отношению < M, произведенному подклассом гладких и конечно аддитивных моделей. Иными словами, когда язык бесконечен (но счетен), R описывается либо через отношение PM, произведенное конечно аддитивными моделями, либо через отношение < M, произведенное классом конечно аддитивных моделей, являющихся гладкими.

Немонотонное следование и кондиционалы

Ниже на диаграмме представлена иерархия условных систем. Диаграмму следует интерпретировать так: когда система соединена с другой системой восходящими линиями, верхняя представляет собой расширение нижней. Основными системами служат V, NP и B. Путь от B к V обозначает добавление отрицательной транзитивности в качестве ограничения на отношение упорядочивание (см. раздел 3.1.1 выше). Путь от NP к V реализован посредством добавления (L). Система B', включенная в диаграмму, не столь интересна, однако мы добавили ее ради симметрии. Также представлены расширения (T), (TU) и (TA) систем V, NP и B (где «А» означает абсолютность — см. раздел 3.2.1 — «U» — единообразие, а «Т» — полную рефлексивность — см. раздел 3.1.1).

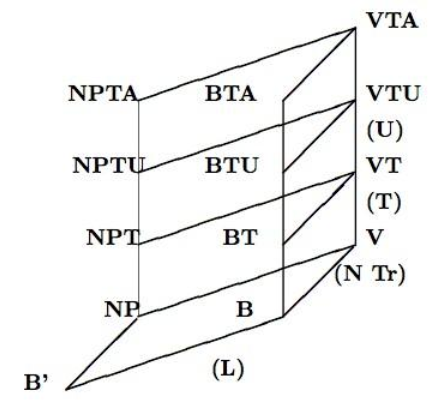
Диаграмма представляет иерархию условных систем сверху вниз по убыванию логической силы. В работе Арло-Косты и Шапиро (Arló-Costa and Shapiro 1992) показано, что положения рациональной системы R можно отобразить в обобщенный роговидный фрагмент системы V и что этот фрагмент сохраняется на протяжении изображенных систем большей логической силы как минимум до VTA. Если устранить (L), мы получим схожую связь с обобщенным роговидным паттерном, который соответствует расширениям NP.

Таким образом, посредством этих отображений и результатов, которые были представлены в предыдущем разделе, мы имеем вероятностные модели для обобщенных роговидных фрагментов логик V Льюиса, NP Делгранда и B Бёрджесса. Ситуация усложняется, если мы начинаем рассматривать итерацию — этой теме посвящен следующий раздел.

Итерированные вероятностные кондиционалы

Вероятностный подход, изложенный выше, может быть охарактеризован следующим образом (где выражение «простые кондиционалы» означает невложенные кондиционалы и где мы в соответствии с устоявшейся конвенцией используем строчные буквы для обозначения предложений и прописные для обозначения пропозиций, выражаемых данными предложениями):

Тест Рамсея для простых кондиционалов вероятности

Простой кондиционал (a > b) принимается относительно P(. | .), если и только если наименьшее ядро P[A] = P(. | . ∩ A) влечет B.

Таков качественный тест, в рамках которого принятие подразумевает «все или ничего». Эта модель избегает приписывания вероятности кондиционалам как такового. Ее можно перефразировать, приписав вероятность 1 невложенным кондиционалам. Мы видели, что такая модель может дать вероятностное описание паттернов вывода хорошо известных немонотонных логик и обобщенных роговидных паттернов вывода соответствующих условных логик.

Мы также убедились, что используемое в таких моделях представление об условной вероятности не имеет ничего общего с основополагающими трудами Колмогорова. Вместо этого речь идет о примитивном понятии конечно аддитивной условной вероятности.

Однако такие модели достаточно ограничены в логическом отношении. Они не могут описать булевы сочетания кондиционалов и элементарные формы итерации, допустимые в рамках таких слабых систем, как V Льюиса и B Бёрджесса. Есть ли у нас вариант получше? В данном разделе будет представлен ряд наработок в этом направлении.

В широко цитируемой статье Макги (McGee 1985) рассматривается проблема итерированных кондиционалов. Макги приводит доводы в пользу так называемой аксиомы экспорта-импорта:

(EI)

(a > (b > c)) ↔ (a ∧ b) > c

Тем не менее аргумент в защиту (EI) — условия, которое не удается валидировать в какой бы то ни было из рассмотренных нами условных логик — не отсылает к вероятностным моделям.

Арло-Коста (Arló-Costa 2001) представляет вероятностную модель, валидирующую аксиому экспорта-импорта. В модели используются несколько понятий, введенных в предыдущих разделах, такие как вероятностные ядра функции условной вероятности. Внутреннее пространство вероятности имеет область U и связанное сигма-поле пропозиций F.

Пусть LC будет наименьшим языком, который расширяет булев язык-основу L так, что если α ∈ L и β ∈ LC, то α > β ∈ LC и ¬β ∈ LC. Мы используем запись T > для обозначения теорий над LC. В модели задействована вероятностная функция поддержки, Sup, из множества функций условной вероятности, определенного над вероятностным пространством для T >. Итак, каждая функция вероятности P(. | .) связана с множеством поддержки, указывающим на множество условных предложений, поддерживаемых P(. | .) или принимаемых относительно P(. | .). Теперь у нас имеется достаточно элементов для того, чтобы определить понятие вероятностной поддержки:

Тест Рамсея для кондиционалов вероятности

(α > β) ∈ Sup(P), если и только если (1) b = β в L и наименьшее ядро для P[A] влевчет B — или же (2) β в LC−L и β ∈ Sup(P[A](X | Y)) = Sup(P(X | Y ∩ A)).

Тест Рамсея для отрицаний кондиционалов вероятности

¬(α > β) ∈ Sup(P), если и только если (1) b = β в L и наименьшее ядро для P[A] не влечет B — или же (2) β в LC−L и β ∉ Sup(P[A](X | Y)) = Sup(P(X | Y ∩ A)).

Если пропозиция A рассекает систему ядер функции P(. | .), то система ядер P[A](. | .) может быть получена из системы ядер P(. | .) путем пересечения каждого из этих ядер с помощью A: эти пересечения и будут системой ядер для P[A](. | .). Итоговое понятие гипотетического пересмотра разрешает аксиомам валидировать (EI).

Логика эпистемических кондиционалов

Петер Гарденфорс (Gärdenfors 1978, 1988) предложил следующую разновидность теста Рамсея (концептуальное его описание см. во введении к данной статье):

(ГТР)

a > b ∈ K, если и только если b ∈ K*a.

Данная формулировка теста подразумевает, что язык-основа содержит кондиционалы (с итерацией или без). Мы назовем его L>. Исходный внутренний булев язык будет называться L0. Ниже мы рассмотрим вспомогательные условные языки, содержащие условные фрагменты L>.

Прежде всего мы обсудим два основных постулата для пересмотра убеждений, которые затрагивают ограничения непротиворечивости. Первый из них устанавливает, что следствие пересмотра любой теории с непротиворечивым предложением ведет к непротиворечивым выходным данным. Разумеется, они включают противоречивую теорию, которую мы обозначим K⊥.

Второй постулат куда менее интуитивен. Он гласит, что результат пересмотра противоречивой теории всегда неудачен, поскольку теория остается неисправленной. В настоящее время постулат представляет для нас лишь формальный интерес. Однако позднее, когда мы затронем теорию под названием UPDATE, постулат получит интуитивную интерпретацию (хотя и не эпистемическую). 

(Непротиворечивость)

Если a непротиворечива, то K*a ≠ K⊥.

(US)

Если K = K⊥, то K*a = K⊥.

Непротиворечивость — обычное ограничение, накладываемое на теории пересмотра убеждений наподобие АГМ (Alchourrón, Gärdenfors, and Makinson 1985). Наш первый результат показывает, что тест Рамсея в версии Герденфорса вступает в противоречие с постулатом успешности:

Теорема 3 (Arló-Costa 1990). (ГТР), взятый вместе с постулатом непротиворечивости, несовместимым с непротиворечивостью лежащего в основе представления о логическом следовании.

Доказательство. Сначала выведем (US) из (ГТР). Допустим, что K = K⊥. Тогда для всех b, a > b в K, согласно (ГТР), мы получим, что для всех b верно b ∈ K*a. Рассмотрим следующий пример (Непротиворечивость): Если ⊬ ⊥, то K⊥*T ≠ K⊥. Поскольку лежащее в основе понятие следования непротиворечиво, мы имеем K⊥*T ≠ K⊥. Однако, по (US), мы получаем K⊥*T = K⊥.

Релевантность этой теоремы, которая на первый взгляд слишком уж зависит от предельных случаев, станет очевидной в ходе дальнейшего изложения. А пока для начала мы обратимся к другому заключению о несовместимости, первоначально доказанному Гарденфорсом (Gärdenfors 1988).

Чтобы оценить значение этого результата, будет полезно напомнить читателю, что в своей книге и в статьях о кондиционалах Герденфорс прежде всего намеревался использовать свой тест принятия в качестве семантического моста, который бы объединил логические свойства кондиционалов с основными свойствами пересмотра в аксиоматизации АГМ (Alchourrón, Gärdenfors, and Makinson 1985). Некоторые из таких свойств представлены ниже:

Замыкание

K*a — логическая теория

Успешность

a ∈ K*a

Непротиворечивость

Если a непротиворечиво, то и K*a тоже

Расширение

K*a ⊆ K+a

Сохранение

Если ¬a ∉ K, то K ⊆ K*a

Эквивалентность

Если a и b логически эквивалентны, то K*a = K*b

K+a, расширение K посредством a, получается при принятии логических следствий теоретико-множественного объединения K and {a}. Теперь мы можем ввести важное понятие, а именно модель пересмотра убеждений (МПУ). МПУ — это пара ⟨K, *⟩, где K представляет собой множество убеждений, сконструированных над L>, а * — это функция пересмотра убеждения. Мы допускаем, что каждая K ∈ K удовлетворяет (ГТР). Мы также допускаем, что K замкнуто относительно расширений и пересмотров.

МПУ ⟨K, *⟩ нетривиально, если и только если K ∈ K и существуют три предложения, которые несовместимы попарно, и в K нет их отрицаний. С этими элементами мы можем установить результат, первоначально изложенный Герденфорсом, а именно:

Теорема 4 (Gärdenfors 1988; Hansson 1999: 364–365). Нет таких нетривиальных МПУ, где оператор пересмотра удовлетворяет Замыканию, Непротиворечивости, Успешности и Сохранению.

Доказательство. Допустим от противного, что существуют МПУ ⟨K, *⟩ и K ∈ K, равно как и три предложения a, b, d, которые удовлетворяют условиям нетривиальности. Все предложения a, b, d непротиворечивы.

Теперь рассмотрим множество убеждений (K*a)*(b ∨ d). Под замыканием относительно пересмотров (K*a)*(b ∨ d) ∈ K. Непротиворечивость b гарантирует непротиворечивость (b ∨ d). Следовательно, также непротиворечиво (K*a)*(b ∨ d) (согласно Непротиворечивости). По Успешности, (b ∨ d) ∈ (K*a)*(b ∨ d). Без потери общности мы можем допустить, что ¬d ∉ (K*a)*(b ∨ d).

Теперь, при замыкании относительно расширений, мы имеем: K+a и K+(b ∨ a) находятся в K и, по определению расширения, K+(b ∨ a) ⊆ K+a. Учитывая ¬a ∉ K, по Сохранению получаем K ⊆ K*a. Успешность гарантирует, что a ∈ K*A, так что K+a ⊆K*a. Следовательно, K+(b ∨ a) ⊆ K*a.

Теперь обратите внимание, что функция изменения, которая используется в МПУ, монотонна: если K ⊆ H, то K*a ⊆ H*a. Мы можем применить монотонность к последнему включению: (K+(b ∨ a))*(b∨ d) ⊆ (K*a)*(b ∨ d). Поскольку без потери общности мы допустили, что ¬d ∉ (K*a)*(b ∨d), мы можем заключить: ¬d ∉ (K+(b ∨ a))*(b ∨ d). В остальном доказательство сводится к демонстрации, что ¬d ∈ (K+(b ∨ a))*(b ∨ d).

Для начала предположим от противного, что ¬(b ∨ d) ∈ K+(b ∨ a). Это эквивалентно допущению, что ¬b ∧ ¬(a ∧ d) логически следует из K. Поскольку a ∧ d противоречиво, отсюда вытекает, что ¬b следует из K, что идет вразрез с нашим применением нетривиальности. А значит, ¬(b ∨ d) ∉ K+(b ∨ a).

Теперь мы можем применить Сохранение и заключить, что K + (b ∨ a) ⊆ (K + (b ∨ a))*(b ∨ d). Успешность дает нам (b ∨ d) ∈ (K+(b ∨ a))*(b ∨ d). Из нетривиальности получаем: K+ b = (K + (b ∨ a))+(b ∨ d) ⊆ (K + (b ∨ a))*(b ∨ d). Итак, должно выйти, что b ∈ (K + (b ∨a))*(b ∨ d). Поскольку из нетривиальности получаем, что b влечет за собой ¬d, отсюда следует, что ¬d ∈ (K+(b∨ a))*(b ∨ d). Это противоречие завершает доказательство.

Заключение о невозможности было представлено в работе Гарденфорса (Gärdenfors 1988) как результат конфликта между постулатом Сохранения и его версией теста Рамсея. Только что доказанная невозможность требует, тем не менее, многих других допущений — от замыкания относительно расширений и пересмотров до непротиворечивости. Существуют более сильные версии заключения о невозможности, которые прибегают к более слабым допущениям (см. блестящий разбор доказательств альтернативных разновидностей теоремы о невозможности в работе Кросса и Ньюта (Cross and Nute 2001)). Существует один вариант заключения, который напрямую затрагивает противоположность сохранения и (ГТР). 

Для начала рассмотрим такое ограничение пересмотров:

Открытое сохранение

Если a, ¬a ∉ K, то K+a ⊆ K*a.

Основная идея состоит в следующем: когда агентом подвешивается предложение a, пересмотры совершаются посредством расширений. Открытое сохранение — это условие, которое вытекает из воззрений самого Рамсея на кондиционалы. Итак, агент, для которого подвешено предложение a, принимает «Если a, то b» относительно эпистемического состояния K, если и только если B принадлежит состоянию убеждения, полученному после добавления a к K. Если таково минимальное условие адекватности для теста на принятие, то (ГТР) ему не удовлетворяет. Для начала нам следует установить подходящие условия нетривиальности. Следующее определение предоставляет нам нетривиальность, которая потребуется нам ниже для Теоремы 5. Понятие нетривиальности, используемое нами в этом результате, не следует путать с понятием нетривиальности, которое было применено в Теореме 4 выше.

Определение 10. Любая МПУ ⟨K, *⟩, которая подчиняется следующим ограничениям, будет называться нетривиальной: (а) язык-основа обладает по меньшей мере двумя различными пропозициональными переменными a и b (отличными от констант ⊥ и ⊤), и K содержит по меньшей мере одно K такое, что (б1) (¬a ∨ b) ∉ K и (б2) (¬a ∧ b) → (a > ¬b) ∉ K.

Условие (б1) не требует особого обоснования. Условие (б2) также вполне умеренно. Собственно, формула (¬a ∧ b) → (a > ¬b) — это не теорема в рамках какой бы то ни было из хорошо известных систем условной логики (эпистемической или нет).

Теорема 5 (Arló-Costa and Levi 1996). Не существует таких нетривиальных МПУ, где бы выполнялся постулат Открытого сохранения.

Напоминаем читателю, что предшествующие результаты применяли МПУ и потому допускали замыкание относительно расширений, то есть если K ∈ K для фиксированной МПУ с универсумом K, то любое расширение K также является множеством допустимых убеждений в МПУ. Многие авторы (напр., Росс (Ross 1989), Ханссон (Hansson 1992), Морро (Morreau 1992) и Макинсон (Makinson 1990)) полагают, что постулат замыкания относительно расширений неоправдан. Интуитивное основание здесь заключается в том, что множество убеждений, включающее кондиционалы, ведет себя совершенно иначе по сравнению с множеством убеждений, состоящим исключительно из «индикативных» предложений, принадлежащих чисто булевому языку. Таким образом, в особенности когда интерпретация условных предложений аутоэпистемична и вследствие этого подспудно зависит от теории референции, добавление индикативного предложения, совместимого со всеми ранее поддержанными индикативами, обычно изымает поддержку условных предложений, поддержанных текущей теорией (и потому являющихся ее элементами). Расширения перестают быть непроблематическими добавлениями. Они также ведут к изъятиям в условной части текущей теории.

Наша последняя теорема также предполагает, что пока сохраняется замыкание относительно расширений, (ГТР) оказывается совместимым с не-байесовскими представлениями о пересмотре, в которых нарушается Открытое сохранение, — то есть (ГТР) совместим с такими понятиями изменения, где пересмотр открытого эпистемического состояния K относительно предложения a (и его отрицания) приводит нас не к расширению K + a, но к более слабому, чем расширение, изменению (в котором информация, содержащаяся в K + a, изымается). Итак, если мы собираемся использовать МПУ для развития семантики кондиционалов, то имеется два основных способа решения парадокса Герденфорса. Один из них состоит в преобразовании МПУ и наложении ограничений на замыкание относительно расширений; при этом сохранение и другие стандартные постулаты пересмотра по-прежнему будут выполняться. Другое решение заключается в том, чтобы оставить замыкание и при этом ослабить постулат сохранения, который утверждает, что если множество убеждений K ∈ K открыто относительно предложения a, то пересмотр происходит путем расширений.

Третье возможное решение состоит в том, чтобы отбросить (ГТР) — а, следовательно, и перестать использовать немодифицированную версию герденфорсовских МПУ. Одна из конкретных альтернатив — принятие теста Рамсея в варианте Леви, который позволяет отделить множества убеждений от поддерживаемых ими кондиционалов. Идея заключается в том, что принципы пересмотра убеждений применяются только к тем множествам убеждений, которые свободны от кондиционалов. Мы рассмотрим данную альтернативу ниже, а сейчас обсудим первые две.

Исходная семантическая программа, которой вдохновлялся Герденфорс, предполагала использование (ГТР) в качестве моста, который выводит формальные ограничения на кондиционалы, когда мы вводим базовые ограничения на убеждения. Тем не менее мы уже видели, что (ГТР) несовместим с Непротиворечивостью и с Открытым сохранением — двумя базовыми ограничениями, накладываемых на пересмотр.

И все же тест можно применить иначе. Вместо того, чтобы фиксировать понятие пересмотра и искать ограничения на кондиционалы, мы можем зафиксировать условную систему, такую как VC Льюиса, и определить, какое именно понятие пересмотра нам потребуется для эпистемической валидации всех аксиом этой системы посредством (ГТР). Мы знаем, что итоговое понятие изменения не будет обладать некоторыми основными свойствами стандартного понятия пересмотра. Оно будет отличаться от него и иметь иную мотивацию. Арло-Коста и Леви (Arló-Costa and Levi 1996) показали, что требуемое понятие изменение — это понятие обновления, предложенное информатиками Х. Катсуно и А. Мендельзоном (Katsuno and Mendelzon 1991).

(U0)    

Для каждого предложения a ∈ L> и каждой условной теории K верно, что K*a — условная теория.

(U1)

a ∈ K*a.

(U2)

Если a ∈ K, то K*a = K.

(U3)

Если a ∈ K*b и b ∈ K*a, то K*a = K*b.

(U4)

K*(a ∧ b) ⊆ (K*a)+b.

(U5)

Если K максимальное и непротиворечивое множество условных убеждений и ¬b ∉ K*a, то (K*a)+b ⊆ K*(a ∧ b).

(U6)

K*a = ∩{W*a : K ⊆ W, и W максимальна и непротиворечива}.

(U7)

Если a и K непротиворечивы, то K*a непротиворечива.

Первых шести постулатов достаточно для валидации логики Льюиса VC. Обратите внимание, что роль постулата (U2) отличается от роли постулатов Сохранения или Открытого сохранения в рамках теории АГМ и прочих стандартных разновидностей пересмотра убеждений. Когда K = K⊥, мы имеем дело с частным случаем постулата неуспешности (US), рассмотренного выше: K*a = K⊥. Монотонность (если K ⊆ H, то K*a ⊆ H*a) также является теоремой при данном понятии обновления. Итак, два свойства, выводимых из (ГТР), — монотонность и неуспешность — присущи понятию изменения, требуемому для валидации всех аксиом системы VC.

Обновление во многих важных аспектах связано с понятием изменения, предложенным Льюисом (Lewis 1976) для придания смысла тезису, согласно которому вероятность кондиционалов соответствует условной вероятности в том или ином ее представлении. Проблема, затронутая Льюисом, весьма схожа с рассматриваемой нами. Льюис показывает, что вероятность кондиционалов — это не стандартная условная вероятность. Однако имеется понятие изменения вероятности, отличающееся как от колмогоровского понятия условной вероятности, так и от понятия де Финетти. Льюис именует его изображением (imaging). Посредством него мы можем сказать, что вероятность кондиционалов совпадает с соответствующим отклоняющимся понятием условной вероятности. Точно так же мы скажем, что уверенность в кондиционалах можно было бы представить в виде отклоняющегося понятия условной уверенности, которое было обеспечено Обновлением. Связи между обновлением и изображением некоторое время упускались из виду, пока информатики, работающие с моделями обновления, не ознакомились с трудами философов.

Тем не менее вопрос остается нерешенным. Существует ли такой тест на принятие, удовлетворяющий условиям адекватности, приведенным выше, с помощью которого мы могли бы продолжить семантическую программу Герденфорса? Ответ — да. Такой тест был предложен во введении к настоящей статье: в сущности, это разновидность теста, первоначально выдвинутого Леви (Levi 1988). Данный способ проверки обходит известные парадоксы (заключения о невозможности) — и благодаря ему мы можем сосредоточиться на высокомотивированном понятии суппозиции и соответствующих условных аксиомах, как и желал Герденфорс.

Эпистемическая валидность

В данном разделе мы исследуем две эпистемические системы, впервые выдвинутые Арло-Костой в работе 1995 года (Arló-Costa 1995). Пусть L> будет наименьшим языком, таким что: (1) L0 ⊆ L>, (2) если a, b ∈ L>, то a > b ∈ L>, и (3) L> замкнут относительно булевых связок. Такой язык слишком силен для целей нашей статьи. Поэтому мы сначала разберем невложенные версии условного языка, которые позднее расширим. Следовательно, мы будем говорить о языке FL>. Пусть FL> будет наименьшим языком, таким что: (1) L0⊆ FL>, (2) если a, b ∈ L0, то a > b ∈ FL>, и (3) FL> замкнут относительно булевых связок. Пусть f-вхождение (плоское вхождение) условной формулы языка FL> будет подстановочным вхождением формулы, где формулы L0 заменяют схемы переменных, встречающиеся в формуле. Вдобавок мы будем называть «плоской» всякую условную формулу, принадлежащую FL>.

Определение 11. Эпистемическая модель (ЭМ) — квадриплет ⟨K, *, s, +⟩, где K — множество множеств убеждений (теорий), * — функция пересмотра убеждений *: K × L0 → K, s — функция поддержки s: K → T>, а + выступает функцией расширения. * и s ограничиваются следующими условиями (c1)–(c3), а также (ЛТР) и (ЛОТР) в формулировке, указанной ниже. K замкнуто относительно пересмотров и расширений.

(c1)

Если A ∈ L0 и A ∈ s(K), то A ∈ K.

(c2)

K ⊆ s(K), независимо от (не)противоречивости K.

(c3)

s(K) — логически замкнутое множество предложений.

(ЛТР)

Если A, B ∈ L0, то (A > B) ∈ s(K) тогда и только тогда, когда B ∈ K*A, независимо от (не)противоречивости K.

(ЛОТР)

Если A, B ∈ L0, то ¬(A > B) ∈ s(K) тогда и только тогда, когда B ∉ K*A, независимо от (не)противоречивости K.

Определение 12. Для каждого A ∈ FL> и каждой M = ⟨K, *, s⟩ a удовлетворяется в M, если существует непротиворечивое K ∈ K, такое что a ∈ s(K). a положительно валидна в M, если a ∈ s(K) для всякого непротиворечивого K ∈ K. a положительно валидна во множестве моделей S, если и только если для каждой модели M в S a положительно валидна в M. Наконец, a эпистемически валидна (э-валидна), если a положительно валидна во всех эпистемических моделях.

Теперь рассмотрим следующую синтаксическую систему:

T

Все классические тавтологии и их подстановочные вхождения в L>

I

a > ⊤

CC

((a > b) ∧ (a > c)) → (a > (b ∧ c))

RCM  

Если ⊢ b → c, то ⊢ (a > b) → (a > c)

M

Modus ponens

Рассмотрим также следующую плоскую версию правила вывода RCM (обозначим ее RCMf):

RCMf

Если ⊢ b → a и a, b, c ∈ L0, то ⊢ (a > b) → (a > c).

CM теперь можно определить как наименьшее множество формул в языке FL>, замкнутое относительно RCMf и M и содержащее все f-вхождения аксиом I и CC, а также все классические тавтологии и их подстановочные вхождения в языке FL>.

Теорема 6. Условная плоская формула a э-валидна, если и только если a является теоремой в CM.

Более сильные условные системы можно получить путем наложения соответствующих ограничений на понятие пересмотра убеждений (или суппозиции), используемое в эпистемических моделях. Одной из значимых систем является EF, которую можно получить из CM при добавлении невложенных вхождений ID, MP, CA, CV и CD: ¬(a > ⊥) для всех нетавтологичных a в аксиоматический базис CM, а также правила вывода RCEAf (как RCMf, это случай RCEA, где все предложения, встречающиеся в правиле, принадлежат L0) к правилам вывода CM.

Понятие суппозиции, требуемое для валидации EF, использует ряд основных постулатов пересмотра АГМ: Успешность, Расширение, Эквивалентность и ослабленную версию непротиворечивости, которая требует непротиворечивости K*a, когда и вводная a, и референтная теория K непротиворечивы. В нем также применяются следующие два постулата АГМ:

(K*7)

K*(a ∧ b) ⊆ (K*a)+b

(K*8)

Если ¬b ∉ K*a, то (K*a)+b ⊆ K*(a ∧ b)

Обратите внимание, что постулат Сохранения не соответствует положительной валидности любой невложенной условной формулы. Модель тем не менее совместима с Сохранением, и его добавление к модели оказывает воздействие на положительную валидность вложенных формул кондиционалов (см. Теорему 8.1 и Наблюдение 8.3 в работе Арло-Косты (Arló-Costa 1995), равно как и обсуждение в разделе 2.7 в работе Кросса и Ньюта 2001 года (Cross and Nute 2001)).

Отрицательная валидность

Для начала рассмотрим следующую «отрицательную» разновидность эпистемической валидности.

Определение 13. Предложение a языка FL> отрицательно валидно в ⟨K, *, s⟩, если ¬a ∉ s(K) для каждого непротиворечивого K ∈ K. Предложение a языка FL> э–-валидно, если оно отрицательно валидно во всякой модели.

В статье Арло-Косты и Леви (Arló-Costa and Levi 1996) показывается, что отрицательная и положительная валидности не совпадают. К примеру, рассмотрим следующее ограничение, накладываемое на модели пересмотра убеждений:

(wp)

Если a ∈ K и K непротиворечивы, то K+a ⊆ K*a.

Обратите внимание, что теперь можно продемонстрировать:

Лемма 7. Все вхождения ((a ∧ b) → (a > b)) в FL> отрицательно валидируются в модели M, если и только если M удовлетворяет (wp).

Следует ли всякому рациональному агенту, чьи обязательства по отношению к изменению ограничиваются по меньшей мере базовыми постулатами АГМ, принимать любой неитерированный случай ((a ∧ b) → (a > b))? Ответ — нет. К примеру, рассмотрим ситуацию агента, для которого a подвешено. Предположим от обратного, что агент принимает все неитерированные вхождения ((a ∧ b) → (a > b)). Тогда если K представляет текущие убеждения, мы знаем, что a ∉ K и ¬a ∉ K. Более того, поскольку мы также допустили, что обязательства по отношению к изменению подчиняются по меньшей мере базовым постулатам АГМ, a ∉K*⊤ и ¬a ∉ K*⊤. Следовательно, по (ЛОТР), ¬ (⊤ > a) ∈ s(K). Поскольку все неитерированные вхождения ((a ∧ b) → (a > b)) принадлежат s(K), a → (⊤ > a) ∈ s(K). А значит, ¬a ∈ K, вопреки нашей исходной гипотезе. Заключение: неверно, что все неитерированные случаи ((a ∧ b) → (a > b)) положительно валидны. Обратите внимание, однако, что если агент принимает конъюнкцию (a ∧ b) (где a, b ∈ L0), он также должен принять (a > b).

Арло-Коста и Леви (Arló-Costa and Levi 1996) приводят доводы в пользу использования положительной, а не отрицательной валидности. Основная идея состоит в том, что существуют эпистемические модели (проходящие тест Рамсея для отрицаний кондиционалов), где правило вывода modus ponens не сохраняет отрицательную валидность.

В герденфорсовских МПУ, которые несовместимы с «отрицательными» версиями теста Рамсея, отрицательная и положительная валидности совпадают, а льюисовскую систему VC можно эпистемически смоделировать посредством обращения к понятию обновления.

Понятие суппозиции у Леви и в АГМ

С эпистемологической точки зрения, функция пересмотра, применяемая в рассмотренными нами моделях, подразумевает понятие суппозиции, подходящее для эпистемических кондиционалов. В таком случае можно задать нормативный вопрос: какие именно базовые аксиоматические ограничения соответствуют такому понятию суппозиции?

Мы видели, что понятие суппозиции, используемое в герденфорсовских эпистемических моделях системы VC Льюиса, не совпадает с теорией АГМ. Как мы уже указывали, аксиома Сохранения и тест Рамсея в версии Герденфорса вступают в конфликт. Соответствующие аксиомы совпадают с понятием обновления Катсуно и Мендельзона, которое в аксиоматическом и концептуальном отношении сильно отличается от АГМ. Можно было бы сказать, что эти аксиомы представляют понятие суппозиции, задействованное в оценке кондиционалов, которые в досистематическом рассмотрении оказываются носителями значений истинности.

Эпистемические модели, задействующие функции поддержки, которые мы изложили выше, совместимы с основными аксиомами АГМ. Неясно, однако, желательно ли их использовать в качестве базовых ограничений на суппозицию. Айзек Леви (Levi 1996) выдвинул положительные аргументы в пользу понятия эпистемической суппозиции, которое не совпадает с АГМ. Мы рассмотрим его доводы в настоящем разделе.

Сначала Леви предлагает механизм суппозиции, который развертывает основные идеи, изложенные ранее Рамсеем в примечании к своей статье. Обратите внимание, что в двух из рассматриваемых Рамсеем случаев суппозиция обладает эпистемологическим значением, а именно когда для агента, который оценивает кондиционал, подвешен антецедент кондиционала и когда агент находится в контрдоксической позиции, то есть уверен в отрицании антецедента.

В первом случае Рамсей, по всей видимости, принимает условие, названное нами Открытым сохранением:

Открытое сохранение

Если a, ¬a ∉ K, то K+a ⊆ K*a.

Второй случай более сложный: в нем подразумевается участие в настоящем пересмотре, а не просто расширении. Тем не менее есть и пределеьный случай, упущенный Рамсеем: как нам следует понимать акт полагания (суппозиции) a, когда агент уже убежден в a?

Первый вариант действий: заявить, что это вырожденный предельный случай и что в нем агенту вовсе не требуется преобразовать текущее эпистемическое состояние. Такой курс взят на вооружение процедурой обновления Катсуно и Мендельзона, хотя при этом она отбрасывает Открытое сохранение.

Однако есть и второй вариант ответа. Идея заключается в том, чтобы симулировать сомнение в истинности a посредством удаления как a, так и его отрицания из текущего состояния уверенности, а затем претворить рекомендуемое Рамсеем расширение относительно видоизмененного состояния. Данная стратегия принимает Открытое сохранение, однако отказывается и от Слабого сохранения (wp), и от аксиомы (U2) обновления.

Таким образом, позиция Леви удерживает слабую версию Сохранения, хотя и не ту ее разновидность, которая удерживается при обновлении. Подход Леви полностью противоположен направлению исследований, начало которому положили обновление и изображение, поскольку он удерживает обстоятельную эпистемическую точку зрения относительно акта полагания (суппозиции), участвующего в оценке кондиционалов.

Обратите внимание, что АГМ не принимается ни Леви (чтобы представить понятие эпистемической суппозиции), ни Герденфорсом (чтобы кодировать онтическое понятие полагания, участвующего в оценке кондиционалов Льюиса). Понятие суппозиции, судя по всему, подчиняется собственным аксиомам, которые необязательно совпадают с аксиомами, описывающими диахроническое изменение убеждений.

Важнейшая составляющая модели Леви — понятие сжатия, требующееся для симуляции сомнения относительно истинности предмета убеждения. Одна из значимых характеристик моделей Леви заключается в том, что они опираются на техники теории принятия решений — и это касается не только сжатия, но и расширения, которое у Леви предстает видом индукции (см. Levi 1996).

Благодаря анализу индуктивных моделей в книге Леви (Levi 1996) появились работы, развивающие индуктивные модели для немонотонного вывода. Такого рода вывод разделяет множество формальных характеристик с логикой умолчаний Рейтера. Он мало чему подчиняется помимо аксиомы под названием Сечение: 

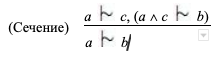
Итерация

Выше разбирались условные эпистемические системы, сконструированные над невложенными языками. В данном разделе мы сосредоточимся на слабейшей системе итерированных кондиционалов, обусловленной эпистемическими моделями. Рассматриваемый проект взят из работы Арло-Косты 1999 года (Arló-Costa 1999a).

Эпистемическая модель (ЭМ) — это квадриплет⟨E, ρ, s, *⟩, где E — множество (эвристически: множество эпистемических состояний); ρ —функция ρ: E → TL0; s — функция s: E → TL>, где TL> обозначает теории, которые можно сконструировать над L>; а * — это функция *: E × L> → E. E замкнуто относительно пересмотров, B = Rng(ρ) замкнуто относительно расширений. Функции ρ, s и * подчиняются следующим двум ограничениям, а также ИТР и ИОТР:

(c1)

Если a ∈ L0 и a ∈ s(E), то a ∈ ρ(E).

(c2)

ρ(E) ⊆ s(E).

(ИТР)

(a > b) ∈ s(E), если и только если b ∈ s(E*a), где E непротиворечиво.

(ИОТР)  

¬(a > b) ∈ s(E), если и только если b ∉ s(E*a), где E непротиворечиво.

В этой модели единственными эпистемическими примитивами выступают состояния в E. Они могут быть теориями, или системами ранжирования, или даже функциями вероятности. Функция ρ дает множество твердых убеждений ρ(E), которых придерживается агент в эпистемическом состоянии E. Функция s дает кондиционалы, которые поддерживаются в состоянии E. Наконец, функция пересмотра убеждений отображает пары эпистемических состояний и предложений L> в эпистемические состояния.

Для каждой a ∈ L> и каждой M = ⟨E, ρ, s, *⟩ a удовлетворима в M, если существует непротиворечивое E ∈ E, такое что a ∈ s(E). a валидна в M, если a ∈ s(E) для всякого непротиворечивого E ∈ E. a валидна в множестве моделей S, если и только если для каждой модели M в S валидна a в M. a валидна, если она валидна во всех моделях. Наконец, a эпистемически влечет b в M = ⟨E, ρ, s, *⟩ тогда и только тогда, когда для всякого E в E a ∈ s(E), b ∈ s(E).

Для начала нам следует определить условный язык, меньший, чем L>. Пусть BC будет наименьшим языком, таким что если a, b ∈ L0, c, d ∈ BC, то a > b, c > d, ¬c, c ∧ d ∈ BC. Теперь рассмотрим условную систему ECM. ECM — наименьшее множество формул в языке L>, замкнутом относительно (RCM) и (M) и содержащим все вхождения аксиом (I), (CC), (F), а также все классические тавтологии и их подстановочные вхождения в языке L>.

I

a > ⊤

CC

((a > b) ∧ (a > c)) → (a > (b ∧ c))

F

¬(a > c) ↔ (a > ¬c), где c ∈ BC

M

Modus ponens

RCM  

Если ⊢ b → c, то ⊢ (a > b) → (a > c)

Следующее заключение о полноте показывает совпадение теорем системы ECM и кондиционалов, валидированных в эпистемических моделях.

Теорема 7. Формула a языка L> валидна, если и только если a выступает теоремой в ECM.

Изложенные результаты демонстрируют базовую логическую структуру итерированных кондиционалов, валидированных в итерированных разновидности теста Рамсея по версии Леви. Аксиома F выводима в очень сильных системах, таких как C2 Сталнакера, но за исключением этого предельного случая она невыводима в большинстве онтических условных систем, обсуждавшихся выше. По всей видимости, отсюда следует, что логическая структура итерированных эпистемических кондиционалов отличается от логической структуры большинства онтических систем, рассматривавшихся в литературе.

Другие вопросы

Один из вопросов, затронутых нами лишь мельком, касался моделей с индикативными кондиционалами. Похоже, в самой активной области исследований по данной теме делается упор на вероятностные модели того типа, который рассматривался нами выше. В самом деле, одно из наиболее прямых приложений вероятностной семантики, разработанной Адамсом, Макги и др., ассоциировалось с предоставлением семантики для индикативных кондиционалов. Это верно, даже если учесть, что некоторые грамматики, такие как Дадмэн (Dudman 1991), ставили под сомнение различие между изъявительным (индикативным) и сослагательным (субъюнктивным) наклонениями в английском языке (которое столь четко проявляется во множестве других индоевропейских языков).

В рамках второго направления исследований, посвященных семантике индикативных кондиционалов, утверждается, что индикативные и материальные импликации имеют одинаковые условия истинности. Эта позиция отстаивалась Льюисом (Lewis 1973) и Джексоном (Jackson 1987). Тем не менее имеются очевидные примеры, опровергающие этот тезис, представленные, к примеру, в разделе 1.10 работой Кросса и Ньюта (Cross and Nute 2001). Примеры показывают, что контрапозиция нарушается в случае некоторых индикативных кондиционалов.

(1) Если после трех часов, то не сильно позже трех часов.

(2) Если сильно позже трех часов, то это не после трех часов.

Данный пример, выдвинутый в той же работе, призван показать, что даже если при некоторых обстоятельствах уместно утверждать (1), это не переносится автоматически на (2). Линия защиты против примеров подобного рода, которой придерживается Грайс (Grice 1991) и Льюис (Lewis 1973), такова: следует тщательно отделять условия утверждения и условия истинности. Правила утверждения могут затем применяться для опровержения: пускай даже (2) буквально истинно, утверждать (2) было бы неуместно.

Третье направление исследований, посвященных индикативным кондиционалам, возникло благодаря работам Сталнакера (Stalnaker 1991) и Дэвиса (Davis 1979). Основная идея состоит в применении семантики, опирающейся на функции выделения, и к индикативам, и к субъюнктивам — различия наклонений предположительно соответствуют различиям свойств функций выделения мира, используемых в семантике каждой разновидности кондиционалов.

Сталнакер начинает анализ с контекстного множества возможных миров, не исключаемых заранее принятой и широко разделяемой фоновой информацией. Идея семантики индикативных кондиционалов заключается в том, что при оценке их в мирах контекстного множества выделенный мир должен — если это возможно — также находиться в контекстном множестве. Иными словами, внутри контекстного множества все миры располагаются ближе друг к другу, чем миры за его пределами. Сослагательное наклонение в английском и других языках, напротив, может быть понято как конвенциональное устройство, указывающее на подвешенность пресуппозиций. Разумеется, в случае индикативных кондиционалов из этого следует, что функция выделения, используемая для их оценки, может выходить за пределы контекстного множества.

Четвертое решение было предложено Леви (Levi 1996: sec. 2.5). Леви в общем и целом отстаивает эпистемическую теорию, которая опирается на условия приемлемости, а не истинностную теорию, основанную на функциях выделения. Несмотря на это значительное различие, многое в его теории сходится с предыдущими подходами, главным образом — тезис о существовании таких форм суппозиций, в которых пропозиция полагается истинной в целях аргумента, соотнесенного не с текущим множеством убеждений, но с фоном разделяемых соглашений (или же широко принимаемой заранее информацией). Хотя в своей книге Леви моделирует эту разновидность суппозиций, в вопросе о грамматике он следует за Дадменом и потому не считает, что данный тип суппозиции консенсуса в точности согласуется с употреблением изъявительного наклонения в английском языке.

Арло-Коста предлагает пятый подход, согласно которому разновидность «фактической» суппозиции, задействованная в анализе кондиционалов, моделируется с помощью понятия гипотетического пересмотра, представленного в работе 2001 года (Arló-Costa 2001). При столкновении с процессом суппозиции агент имеет в распоряжении ядерную систему. Миры во внешнем ядре кодируют информацию, которая, по мнению агента, имеется у всех. Система ядер разрешает пересмотр ожиданий, кодированных во внутреннем ядре, когда предмет суппозиции совместим с пресуппозициями, закодированными посредством множества миров, составляющих внешнее ядро. Тем не менее не существует фактической суппозиции с пропозициями, несовместимыми с внешним ядром; такие суппозиции ведут к несогласованности. Данная модель также призвана отразить мысль о том, что индикативная суппозиция — это суппозиция при особом наборе ограничений, источником которых выступают представления агента относительно разделяемых другими агентами соглашений в релевантной популяции.

Дальнейшие сведения об индикативных кондиционалах, в особенности об аргументах в пользу и против их истинностной функциональности, можно найти во втором разделе работы Эджингтона (Edgington 2006). В книге Ликана (Lycan 2001) содержится интересное обсуждение (гл. 7) различия индикатив/субъюнктив, которое поддерживает и дополняет скептические соображения Дадмена касаемо его значения для условных предложений в английском языке. Наконец, в работе Беннетта (Bennett 2003) предлагается общий обзор философских теорий кондиционалов. В книге излагается и оценивается ряд современных теорий индикативов и субъюнктивов, а также позиция самого Беннетта относительно разделения индикатив/субъюнктив.

Структурные контрфактические высказывания и контрфактические высказывания, основанные на подобии

Ф.П. Рамсей в своем знаменитом примечании набросал механизм для оценки контрфактических высказываний. Его мысль заключается в том, что при оценке «Если p, то q» в случае, если «какая-то из сторон уверена в не-р наверняка, вопрос перестает подразумевать для нее нечто еще, кроме вопроса относительно того, что следует из определенных законов или гипотез» (Рамсей 2003: 193). Эта цитата получила множество разных интерпретаций. Согласно одной из них, чтобы получить процедуру для оценки контрфактических высказываний, нам прежде всего требуется хорошая модель механизмов и каузальных законов, действующих в нашем мире. Контрфактические высказывания затем анализируются как «то, что вытекает из» этих законов.

Тем не менее книга Льюиса «Контрфактические высказывания» (Counterfactuals, 1973) положила начало другому направлению исследований. В некотором смысле ее онтологическая программа опрокидывает только что изложенный порядок объяснения. Льюис предлагает интерпретировать «A послужило причиной B» через следующую контрфактическую зависимость: «B не произошло бы, если бы не A». Контрфактическую же зависимость, в свою очередь, нужно трактовать с помощью понятия подобия миров, которое в буквальном смысле берется как основной примитив. Такого рода анализ оставляет понятие подобия безусловным и таинственным. Более того, Файн в своей статье (Fine 1975) выдвигает предположение, что подобие явлений неадекватно. Он рассматривает контрфактическое высказывание, которое большинство из нас сегодня полагает истинным: «Если бы Никсон нажал на кнопку, началась бы ядерная война». Разумеется, мир, где кнопка не нажата, во много раз более схож с нашим миром, нежели тот, где случился ядерный взрыв. Отсюда следует, что степени подобия не могут быть произвольными и что они должны так или иначе соотноситься с нашими интуитивными представлениями о причинно-следственных законах. Льюис в своей статье 1979 года (Lewis 1979) предлагает сложную систему ограничений, различных по весомости и очередности (глубина нарушений законов, или «чудес», соответствие фактам, предшествование во времени и т.п.) Тем самым Льюис пытался согласовать понятие подобия с нашими каузальными интуициями. Но, как отмечалось множеством авторов (см. Woodward 2005: sec. 3.6), по-прежнему проблемы остались.

Был предложен также любопытный альтернативный подход: обратить порядок объяснения в соответствии с исходными идеями, которые были озвучены Рамсеем в примечании. Перл (2000: 239) предлагает ясную формулировку этой идеи:

В отличие от теории Льюиса, контрфактические высказывания [в структурном подходе] не основаны на абстрактном понятии подобия среди гипотетических миров; вместо этого они опираются напрямую на механизмы (или «законы», если угодно), которые производят эти миры, и на их инвариантные свойства. Эфемерные «чудеса» Льюиса теперь замещаются принципиальными микрохирургиями, do(X = x), которые представляют минимальное изменение (каузальной модели) в качестве необходимого для установления антецедента X = x. Итак, подобия и очередности — если они вообще требуются — могут быть вчитаны в оператор do задним числом, однако они не служат основой анализа. (Pearl 2000: 239)

Для такого подхода наиважнейшим является понятие «микрохирургии» или, как его теперь обычно называют, вмешательства (intervention). Представление вмешательств подразумевает, в свою очередь, использование НАГ — направленного ациклического графа — для графической репрезентации каузальных связей. Большая часть современной теории причинности полагается на такие графы.

Понятие контрфактических высказываний, применяемое в приведенном выше анализе Перла, развивается в трех основных книгах. Первая принадлежит Спиртсу, Глимору и Шейнсу (Spirtes, Glymour, and Scheines 2001). Вторая — самому Перлу (Pearl 2000). Третья монография — Вудворда (Woodward 2005) — была издана сравнительно недавно; в ней подробно исследуется понятие вмешательства.

С точки зрения формальной логики, книга Перла предлагает наиболее всесторонний анализ, если аксиоматически сопоставить ее с иерархией кондиционалов Льюиса. Однако, как показывается в статье Гольцшмидта и Перла (Golszmidt and Pearl 1996), данная область сталкивается с многочисленными трудностями, которые так и не были разрешены. Авторы строят предположение о полной характеризации ранжирующих систем, ограниченных связанными НАГ, и выдвигают аксиому Маркова особого рода, в которой эксплицитно говорится о вмешательствах в НАГ. Тем самым, поскольку добавляется третий уровень репрезентации через НАГ, нарушается привычное разделение труда синтаксиса и семантики.

Нам следует хотя бы вскользь упомянуть еще две важные темы. С одной стороны, существуют интересные труды, соотносящие кондиционалы и время, в особенности ветвящиеся временные структуры. Идея состоит в том, чтобы расширить аппарат репрезентации, эксплицитно добавив в него время, а затем использовать эту дополнительную выразительную силу для прояснения отношений подобия между мирами, которые были задействованы в оценке онтических кондиционалов. Превосходный обзор философских наработок в этой области см. в соответствующих разделах статьи Кросса и Ньюта (Cross and Nute 2001). 

Вторая важная область исследований в условной логике затрагивает вопросы о представлении интерактивного знания агентов, которые принимают участие в некооперативных играх с полной и неполной информацией. Как показал в ряде статей нобелевский лауреат Роберт Ауман, материальная импликация — недостаточная структура для анализа игр. Следующий фрагмент демонстрирует значение кондиционалов, которые Ауман называет содержательными:

Возьмем, к примеру, утверждение: «Если белые ходят пешкой, то черный ферзь оказывается в западне». В материальном смысле для истинности здесь достаточно, чтобы белые не ходили пешкой на самом деле. В содержательном смысле мы игнорируем действительный ход белых и представляем, что они ходят пешкой. Если черный ферзь попадает в ловушку, содержательный кондиционал истинен; если нет, он ложен.

Белые не ходят пешкой, и мы можем сказать: «Если бы они пошли пешкой, черный ферзь оказался бы в западне». Так будет звучать контрфактическое высказывание. Чтобы определить его истинность, нам следует представить, что белые сходили пешкой, и убедиться в том, попал ли ферзь в ловушку. (Aumann 1995: sec. 5)

Анализ должен показаться читателю знакомым, хотя неясно, что именно Ауман имеет в виду под «игнорированием действительного хода белых». Можно решить в духе Леви, что здесь подразумевается сжатие всей информации о текущем ходе и последующее непроблематическое добавление информации, в соответствии с которой белые ходят пешкой.

Дов Самет (Samet 1996) предложил конкретную модель представления о гипотетическом знании, которая используется для формулировки эпистемических моделей обратной индукции в рамках игр с полной информацией. Наконец, Брайан Скирмс (Skyrms 1998) выдвинул байесианскую теорию кондиционалов, обобщающую теорию из статьи Зелтена и Леопольда (Selten and Leopold 1988) и подход Сталнакера, опирающихся на функцию выделения. Данная теория сопоставляется с кондиционалами Адамса в статье Скирмса (Skyrms 1994). Согласно Скирмсу, его теория имеет интересные приложения для анализа игр с неполной информацией (анализ игр с полной информацией требует, по его мнению, лишь использования аргументов сведения к абсурду).

Библиография

На русском языке

Поппер К. (2005) Логика научного исследования. М.: Республика, 2005.

Рамсей Ф. (2003) Общие пропозиции и причинность // Он же. Философские работы. Томск: Изд-во Том. ун-та, 2003. С. 185–204.

На английском языке

Adams, E.W. (1965) “On the Logic of Conditionals”, Inquiry, 8: 166-97.

Adams, E.W. (1966) “Probability and the Logic of Conditionals”, 265-316 in Aspects of Inductive Logic, (ed.) J. Hintikka and P. Suppes, Amsterdam: North Holland.

Adams, E.W. (1975) The Logic of Conditionals, Dordrecht: D. Reidel.

Alchourrón, C.E., Gärdenfors, P., Makinson, D. (1985) “On the Logic of Theory Change: Partial Meet Contraction and Revision Functions”, The Journal of Symbolic Logic, 50: 510-530.

Aqvist, L. (1973) “Modal Logic with Subjunctive Conditionals and Dispositional Predicates”, Journal of Philosophical Logic, 2: 1-76.

Arló-Costa, H. (1990) “Conditionals and Monotonic Belief Revisions: The Success Postulate”. Studia Logica, XLIX/4: 557-566.

Arló-Costa, H. (1995) “Epistemic Conditionals”, Snakes and Stars, in Conditionals, from Philosophy to Computer Science, vol. 5 of Studies in Logic and Computation [Series editor: D.M. Gabbay], L. Farinas del Cerro, G. Crocco, A. Herzig (eds.), Oxford: Oxford University Press, 193-239.

Arló-Costa, H. (1999) “Qualitative and Probabilistic Models of Full Belief”, Proceedings of Logic Colloquim '98, Lecture Notes on Logic, 13, S. Buss, P.Hajek, P. Pudlak (eds.), Natick: Mass., ASL in cooperation with A. K. Peters, 1-13.

Arló-Costa, H. (1999a) “Belief Revision Conditionals: Basic Iterated systems”, Annals of Pure and Applied Logic, 96: 3-28.

Arló-Costa, H. (2001) “Bayesian Epistemology and Epistemic Conditionals: On the Status of the Export-Import Laws”, Journal of Philosophy, Vol. XCVIII/11: 555-598.

Arló-Costa, H and I. Levi (1996) “Two Notions of Epistemic Validity”, Synthese, Vol. 109, Number 2: 217-262.

Arló-Costa, H. and R. Parikh (2005) “Conditional Probability and Defeasible Inference”, Journal of Philosophical Logic, 34: 97-119.

Arló-Costa, H. and S. Shapiro (1992) “Maps Between Conditional Logic and Non-monotonic Logic”, in Principles of Knowledge Representation and Reasoning: Proceedings of the Third International Conference, B. Nebel, C. Rich, W. Swartout, (eds.), San Mateo, CA.: Morgan Kaufmann, 553-565.

Aumann, R. (1995) “Backward Induction and Common Knowledge of Rationality”, Games and Economic Behavior, 8: 6-19.

Bennett, J. (2003) A Philosophical Guide to Conditionals, Oxford: Clarendon Press

Burgess, J. (1981) “Quick Completeness Proofs for Some Logics of Conditionals”, Notre Dame Journal of Formal Logic, 22: 76-84.

Butcher, D. (1978) Subjunctive conditional modal logic, Ph.D. Dissertation, Philosophy, Stanford University.

Chellas, B.F. (1975) “Basic Conditional Logic”, Journal of Philosophical Logic, 4: 133-153.

Chellas, B.F. (1980) Modal Logic: An Introduction, Cambridge: Cambridge University Press.

Chisholm, R. (1946) “The Contrary-to-fact Conditional”, Mind, 55: 289-307.

Cross, C. and D. Nute (2001) “Conditional Logic”, in Handbook of Philosophical Logic, volume IV (Revised Edition), D. Gabbay (ed.), Dordrecht: D. Reidel.

Davis, W. (1979) “Indicative and Subjunctive Conditionals”, Philosophical Review, 88: 544-564.

De Finetti, B. (1990) Theory of Probability, Volume I, Wiley.

Delgrande, J. (1987) “A first-order Logic for Prototypical Properties”, Artificial Intelligence, 33: 105-130.

Dubins, L.E. (1975) “Finitely Additive Conditional Probabilities”, Conglomerability, and Disintegrations, Ann. Prob., 3: 89-99.

Dudman, V.H. (1991) “The Interpretation of ‘If’-Sentences”, in F. Jackson (ed.) Conditionals, (Oxford Readings in Philosophy), Oxford: Oxford University Press, 202-233.

Edgington, D., “Conditionals,” The Stanford Encyclopedia of Philosophy (Spring 2006 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/spr2006/entries/conditionals/>.

Eells, E. and B. Skyrms, eds., (1994) Probability and Conditionals: Belief Revision and Rational Decision, Cambridge: Cambridge University Press.

Fetzer, J.H. and D. Nute. (1978) “Syntax, Semantics and Ontology: A Probabilistic Causal Calculus”, Synthese, 40: 453-495.

Fetzer, J.H. and D. Nute. (1980) “A Probabilistic Causal Calculus: Conflicting Conceptions”, Synthese, 44: 241-246.

Fine, K. (1975) “Review of Counterfactuals”, Mind, 84: 451-458.

Gabbay, D.M. (1972) “A General Theory of Conditionals in Terms of a Ternary Operator”, Theoria, 38: 97-104.

Gärdenfors, P. (1978) “Conditionals and Changes of Belief”, in The Logic and Epistemology of Scientific Change, ed. by I. Niiniluoto and R. Tuomela, Acta Philosophica Fennica, 30: 381-404.

Gärdenfors, P. (1988) Knowledge in Flux, Cambridge, MA: MIT Press.

Gärdenfors, P. and S. Lindström, M. Morreau, W. Rabinowicz (1989) ‘The negative Ramsey Test: Another Triviality Result’, in The Logic of Theory Change, A. Fuhrmann and M. Morreau (eds.), Berlin: Springer-Verlag, 129-134.

Gibbard, A. (1981) “Two Recent Theories of Conditionals”, in W. Harper, R. Stalnaker and G. Pearce (eds.), Ifs, Dordrecht: D. Reidel.

Girard, P. (2006) “From Onions to Broccoli: Generalizing Lewis' Counterfactual Logic”, Journal of Applied Non-Classical Logic, 17(2): 213–229.

Goodman, N. (1955) Fact, Fiction and Forecast, Cambridge, MA: Harvard.

Goldszmidt. M. and J. Pearl (1996) “Qualitative Probabilities for Default Reasoning, Belief Revision and Causal Modelling”, Artificial Intelligence, 84, No 1-2: 57-112.

Grice, P. (1991) “Indicative Conditionals”, in Studies in the Way of Words, Cambridge, Mass., Harvard University Press:58-86.

Hájek, A. (1994) “Triviality on the Cheap?” In E. Eells and B. Skyrms (1994), 113-141.

Hájek, A. and N. Hall (1994) “The hypothesis of Conditional Construal of Conditional Probability”, in E. Eells and B. Skyrms (1994), 75-113.

Hall, N. (1994) “Back in the CCCP”, in E. Eells and B. Skyrms (1994), 141-161.

Halpern, J. (2003) Reasoning about Uncertainty, Cambridge Mass.: MIT Press.

Hansson, S.O. (1992) “In Defense of the Ramsey Test”, Journal of Philosophy, 89: 499-521.

Hansson, S.O. (1999) A Textbook of Belief Dynamics: Theory Change and Database Updating, Dordrecth: Kluwer.

Harper, W.L. (1975) “Rational Belief Change”, Popper Functions and Counterfactuals, Synthese, 30: 221-62.

Harper, W.L. (1976) “Ramsey Test Conditionals and Iterated Belief Change”, in Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, (ed.) W. L. Harper and C. Hooker, Dordrecht: D. Reidel, 117-35.

Jackson, F. (1987) Conditionals, Blackwell, Oxford, New York.

Jeffreys, H. (1961) Theory of Probability, New York: Oxford University Press.

Katsuno, H. and A. Mendelzon (1991) “On the Difference Between Updating a Knowledge Base and Revising It”, In Belief Revision, P. Gärdenfors (ed.), Cambridge: Cambridge University Press, pp. 183-203.

Kraus, S., and D. Lehmann, and M. Magidor (1990) “Non-monotonic Reasoning”, Preferential Models and Cumulative Logics, Artificial Intelligence, 44: 167-207.

Kvart, I. (1986) A Theory of Counterfactuals, Indianapolis: Hackett.

Lehmann, D. and M. Magidor (1988) “Rational Logics and Their Models; A study in Cumulative logics”, Technical Report TR 88-16 of the Department of Computer Science, Hebrew University of Jerusalem, November 1988.

Lewis, D. (1973) Counterfactuals, Cambridge, MA: Harvard University Press. Reissued London: Blackwell, 2001.

Lewis, D. (1976) “Probability of Conditionals and Conditional Probabilities”, Philosophical Review, 85: 297-315; reprinted in Harper et al. (eds.) (1981) Ifs, Dordrecht: D. Reidel.

Lewis, D. (1979) Counterfactual Dependence and Time's Arrow. Nous, 13: 455-476.

Lewis, D. (1991) “Probability of Conditionals and Conditional Probabilities II”, F. Jackson (ed.), Conditionals, Oxford: Oxford University Press.

Levi, I. (1977) “Subjunctives, Dispositions and Chances”, Synthese, 34: 423-55.

Levi, I. (1988) “Iteration of Conditionals and the Ramsey Test”, Synthese , 76: 49-81.

Levi, I. (1996) For the Sake of the Argument: Ramsey Test Conditionals, Inductive Inference and Non-monotonic Reasoning., Cambridge: Cambridge University Press.

Lycan, W.G. (2001) Real Conditionals, Oxford: Oxford University Press.

Mackie, J.L. (1962) “Counterfactuals and Causal laws”, in Analytical Philosophy, R.J. Butler (ed.), Oxford: Blackwell, 66-80.

Mackie, J.L. (1972) Truth, Probability and Paradox, Oxford: Clarendon.

Makinson, D. (1990) “The Gärdenfors's Impossibility Theorem in Non-monotonic Contexts”, Studia Logica, 49: 1-6.

McGee, V. (1985) “A Counterexample to Modus Ponens”, Journal of Philosophy, 82: 462-471.

McGee, V. (1994) “Learning the Impossible”, in E. Eells and B. Skyrms (1994), 179-99.

Montague, R. (1970) “Universal Grammar”, Theoria, 36: 373-98.

Morreau, M. (1992) “Epistemic Semantics for Counterfactuals”, Journal of Philosophical Logic, 21: 33-62.

Morreau, M. (1997) “Fainthearted Conditionals”, The Journal of Philosophy, 94: 187-211.

Nozick, R. (1981) Philosophical Explanations, Oxford: Oxford University Press.

Nute, D. (1980) Topics in Conditional Logic, Dordrecht: D. Reidel.

Nute, D. (1981) “Causes, Laws and Statements”, Synthese, 48: 347-370.

Pearl, J. (2000) Causality: Models, Reasoning, and Inference, Cambridge University Press, Cambridge, England.

Pollock, J. (1981) “A refined theory of counterfactuals”, Journal of Philosophical Logic, 10: 239-266.

Rescher, N. (1964) Hypothetical Reasoning, Dordrecht: Reidel.

Rott, H. (1989) “Conditionals and Theory Change: Revisions, Expansions and Additions”, Synthese, 81: 91-113.

Samet, D. (1996). “Hypothetical Knowledge and Games with Perfect Information”, Games and Economic Behavior, 17: 230-251.

Sanford, D.H. (1989) If P, then Q: Conditionals and Foundations of Reasoning, London: Routledge.

Scott, D. (1970) “Advice in Modal Logic,” K. Lambert (Ed.) Philosophical Problems in Logic, Dordrecht: D. Reidel, 143-73.

Seidenfeld, T. and J. Kadane (1984) “The Extent of Non-conglomerability of Finitely Additive Probability”, Probability Theory and Related Fields, 66, Number 2: 205-226.

Seidenfeld, T., M. Schervish and J. Kadane (2006) “Improper Regular Conditional Distributions”, Annals of Probability, 34:1.

Selten, R. and U. Leopold (1982) “Subjunctive Conditionals in Decision and Game Theory”, in W. Stegmuller et al. (eds.) Philosophy of Economics. Berlin, Springer: 199-200.

Skyrms, B. (1987) “Updating, Supposing and MAXENT”, Theory and Decision, 22/3: 225-246.

Skyrms, B. (1994) “Adams's Conditionals”, In E. Eells and B. Skyrms (eds.) Probability and Conditionals: Belief Revision and Rational Decision, Cambridge: Cambridge University Press, 13-27.

Skyrms, B. (1998) “Subjunctive Conditionals and Revealed Preference”, Philosophy of Science, 65/4: 545-574.

Spirtes, P. and C. Glymour, R. Scheines (2001) “Causation, Prediction, and Search”, 2nd Edition, Cambridge, MA: MIT Press.

Stalnaker, R. (1968) “A Theory of Conditionals,” Studies in Logical Theory, American Philosophical Quarterly, Monograph: 2, 98-112.

Stalnaker, R. (1970) “Probability and Conditionals”, Philosophy of Science, 37: 64-80. Reprinted in Harper et al. (eds.) (1981) Ifs, , Dordrecht: D. Reidel.

Stalnaker, R. (1987) Inquiry, Cambridge, MA: MIT Press.

Stalnaker, R. (1991) “Indicative Conditionals”, in F. Jackson (ed.) Conditionals, (Oxford Readings in Philosophy), Oxford: Oxford University Press, 136-155.

Stalnaker, R. and R. Jeffrey (1994) “Conditionals as Random Variables”, in E. Eells and B. Skyrms (eds.) Probability and Conditionals: Belief Revision and Rational Decision, Cambridge: Cambridge University Press, 31-47.

van Fraassen, B. (1976) “Probabilities of Conditionals”, in W.L. Harper and C.A. Hooker (eds.) Foundations of Probability Theory, Statistical Inference and Statistical Theories of Science, Dordrecht: D. Reidel, 261-301.

van Fraassen, B. (1995) “Fine-grained Opinion, Probability and the Logic of Full Belief”, Journal of Philosophical Logic, 24, 349-377.

Veltman, F. (1985) Logics for Conditionals, Ph.D. Dissertation, Philosophy, University of Amsterdam.

Woodward, J. (2005) Making Things Happen: A Theory of Causal Explanation (Oxford Studies in the Philosophy of Science), New York: Oxford University Press.