Интуиционизм в философии математики
Впервые опубликовано 4 сентября 2008 года; содержательно переработано 11 июня 2019 года.
Интуиционизм — это направление в философии математики, зачинателем которого был Л. Э. Я. Брауэр (1881–1966). Интуиционизм основывается на идее о том, что математика является творением нашего ума. Мы можем постичь истинность математических высказываний лишь посредством мысленного построения, доказывающего их истинность, коммуникация же между математиками служит лишь для того, чтобы несколько различных сознаний могли воспроизводить один и тот же мыслительный процесс.
Такой подход к математике имеет далеко идущие следствия для повседневной математической практики, одно из которых состоит в отказе от принципа исключенного третьего (A∨¬A). Действительно, существуют предложения (например, гипотеза Римана), для которых на данный момент не существует ни доказательства, ни опровержения. Коль скоро наличие опровержения некоторого высказывания в интуиционизме позволяет доказать, что это высказывание не истинно, отсюда следует, что и А, ¬A и не выполняются, с точки зрения интуиционизма, по крайней мере на данный момент.
Помимо отказа от принципа исключенного третьего интуиционизм значительно отклоняется от классической математики в том, что касается идеи континуума: с точки зрения интуиционизма, континуум характеризуется тем, что все всюду определенные функции на нем являются непрерывными. Таким образом, в отличие от некоторых других теорий конструктивной математики, интуиционизм не основан на ограничении классической модели вывода. Такой подход идет вразрез с фундаментальными положениями классической математики.
Брауэр посвятил значительную часть свой жизни развитию математики на этом новом основании. Хотя интуиционизму не довелось вытеснить классическую математику, приобретя статус стандартной концепции математики, тем не менее он всегда привлекал к себе огромное внимание и до сих пор является широко изучаемой областью.
В этой статье мы сосредоточимся на аспектах интуиционизма, которые отличают его от других направлений конструктивной математики; и лишь коротко затронем те моменты, которые сближают интуиционизм с прочими формами конструктивизма (например, фундаментальные теории и модели).
Брауэр
Лёйтзен Эгберт Ян Брауэр родился в нидерландском городе Оверши. Он изучал математику и физику в Амстердамском университете, где защитил докторскую диссертацию в 1907 году. В 1909 году он начал преподавать в том же университете, в 1912 году был назначен на полную профессорскую ставку и занимал эту должность вплоть до своего ухода на пенсию в 1951 году. Брауэр был блестящим математиком, который совершил прорыв в области топологии и еще в молодости получил широкую известность. Всю свою жизнь он оставался оригинальным ученым, со страстной увлеченностью исследовавшим свой предмет, что стало причиной конфликтов между ним и многими его коллегами, главным образом — с Давидом Гильбертом. У него также было немало почитателей; он охотно принимал в своем доме — «хижине» — в Бларикюме многих известных математиков того времени. На склоне лет он стал вести все более уединенный образ жизни, но его вера в истинность своих философских идей никогда не угасала. Он погиб в Бларикюме в автокатастрофе в возрасте 85 лет, спустя семь лет после смерти его жены, Лизы Брауэр.
В возрасте 24 лет Брауэр написал книгу «Жизнь, искусство и мистицизм» (Brouwer 1905), солипсистские настроения которой впоследствии найдут отражение в его философии математики. Основные идеи интуиционизма Брауэр впервые сформулировал в своей диссертации, впрочем, окончательную форму, как и свое название, его концепция приобрела несколько позднее. В первые несколько лет после защиты диссертации значительная часть научной работы Брауэра была посвящена топологии — области, в которой он до сих пор остается знаковой фигурой благодаря теории размерности пространства и теореме о неподвижной точке: все это теперь составляет часть классической математики. Впоследствии Брауэр пришел к выводу об ошибочности теоремы о неподвижной точке, впрочем, исходя из установленных им принципов возможно доказательство аналогичного положения, сформулированного через приближения.
Начиная с 1913 года Брауэр все больше времени посвящает дальнейшей разработке идей, сформулированных в его диссертации, развивая полноценную философскую концепцию. На основании введенных им принципов Брауэр корректирует не только философские основания интуиционизма, но также математические концепции, в частности теорию континуума и теорию множеств. К тому времени Брауэр уже был знаменитым математиком, его лекции об интуиционизме, которые он читал в важнейших научных центрах того времени — в Кембридже, в Вене и в Гёттингене — имели широкое влияние.
Среди них был Курт Гёдель — всю жизнь остававшийся убежденным платоником. Герман Вейль как-то написал: «Я отказываюсь от собственной позиции и присоединяюсь к Брауэру» (“So gebe ich also jetzt meinen eigenen Versuch Preis und schließe mich Brouwer an”; Weyl 1921: 56). И хотя в последующие годы Вейль редко обращался к интуиционизму, он никогда не переставал восхищаться Брауэром и его интуиционистской философией математики.
Жизнь Брауэра была наполнена конфликтами. Наиболее тяжелым из них, пожалуй, был конфликт с Гильбертом, который в конце концов привел к тому, что Брауэр был исключен из редакционного совета журнала Mathematische Annalen. Этот конфликт разворачивался в рамках так называемого Grundlagenstreit («спора об основаниях математики»), который потряс общество математиков в начале XX века и возник вследствие открытия парадоксов неконструктивных доказательств в математике. Философы и математики были вынуждены признать недостаточность эпистемологических и онтологических оснований в математике. Интуиционизм Брауэра был одной из философских концепций, стремившихся дать такое основание для математики.
Интуиционизм
Два акта интуиционизма
Согласно Брауэру, математика представляет собой неязыковое творение нашего ума. Время — единственное априорное понятие в кантовском смысле. Брауэр различает два акта интуиционизма:
Первый акт интуиционизма состоит в следующем:
Как мы покажем в разделе, посвященном математике, из первого акта интуиционизма возникают натуральные числа, но этот акт подразумевает строгое ограничение принципов допустимых умозаключений, главным образом — принципа исключенного третьего. Благодаря отказу от этого принципа, а также устранению логического обоснования континуума, говоря словами Брауэра, мы могли бы «опасаться, что интуиционистская математика с необходимостью окажется бедной и анемичной и, в частности, не будет включать в себя анализ» (Brouwer 1952: 142). Второй акт, однако, устанавливает существование континуума — но обладающего свойствами, не присущими континууму в рамках классической математики. Восстановление континуума основывается на понятии последовательности выбора, сформулированного во втором акте, то есть на существовании бесконечных последовательностей, произведенных при помощи выбора, которые, следовательно, не фиксированы заведомо.
Второй акт интуиционизма заключается в следующем:
Два акта интуиционизма закладывают фундамент философии Брауэра: как мы увидим далее, основываясь лишь на этих двух актах, Брауэр выстраивает здание интуиционистской математики. Исходя уже из этих базовых принципов можно заключить, что интуиционизм отличается от платонизма и формализма, поскольку ни в одном из этих направлений не допускается существование математической реальности вне нашего сознания, в них также не предполагается, что математика представляет собой своего рода игру с символами, подчиняющуюся определенным предустановленным правилам. С точки зрения Брауэра, язык используется для того, чтобы обмениваться идеями в математике, однако существование последней независимо от языка. Различие между интуиционизмом и прочими конструктивными подходами к математике, согласно которым математические объекты и аргументы должны быть вычислимы, коренится в свободе, которую второй акт интуиционизма допускает в ходе построения бесконечных последовательностей. Действительно, как мы покажем позднее, следствия из второго акта интуиционизма противоречат положениям классической математики, а стало быть, не будут выполняться для большинства конструктивистских теорий, коль скоро последние составляют часть классической математики.
Таким образом, интуиционизм Брауэра отстоит от прочих направлений философии математики.
Интуиционизм является формой конструктивизма — но лишь в более широком понимании, поскольку многие конструктивисты не принимают всех принципов, которые Брауэр считает истинными.
Творческий субъект
Сами по себе два акта интуиционизма не исключают психологической интерпретации математики. Хотя Брауэр лишь бегло обращается к этому пункту, исходя из его работ в целом ясно, что он не считал, будто бы интуиционизм независим от психологии. Введенное Брауэром понятие «Творящего субъекта» (Creating Subject, Brouwer 1948) — идеализированного сознания, в котором разворачиваются математические построения, — само по себе абстрагируется от несущественных аспектов человеческого мышления, например, от ограниченности пространства и времени и возможных ошибок в аргументации. Таким образом, проблема интерсубъективности, требующая объяснения того обстоятельства, что люди способны коммуницировать, просто-напросто устраняется, поскольку существует только один творящий субъект (в англоязычной литературе также используется понятие Creative Subject, «творческий субъект», но в данной статье используется термин Creating Subject, более близкий Брауэру). В работе Никуса (Niekus 2010) утверждается, что творящий субъект Брауэра не подразумевает идеализированного математика. С точки зрения феноменологического анализа, творящий субъект — это трансцендентальный субъект в гуссерлианском смысле (см. van Atten 2007).
В аргументах, к которым прибегал Брауэр, творящий субъект выстраивал контрпримеры к некоторым недопустимым с точки зрения интуиционизма положениям. Там, где слабые контрпримеры, которые будут приведены ниже, показывают лишь то, что некоторые положения на данный момент недопустимы с точки зрения интуиционизма, понятие идеализированного сознания обнаруживает ложность некоторых принципов классической математики. Пример будет приведен в разделе 5.4, посвященном формализации понятия творящего субъекта; там же приводится объяснение того, что следующий принцип, известный как схема Крипке, можно отстаивать из перспективы творящего субъекта:

A в KS пробегает по множеству формул, а задает свободно становящиеся последовательности — последовательности натуральных чисел, произведенные творческим субъектом, избирающим их элементы один за другим. О свободно становящихся последовательностях и схеме Крипке пойдет речь ниже, в разделе 3.4.
В большинстве философских подходах в математике, например, в платонизме, в математических высказываниях отсутствует временной аспект. В интуитивизме истинность и ложность характеризуются временным аспектом; установленный факт будет оставаться таковым, однако высказывание, доказанное в определенный момент времени, до этого момент будет лишено истинностного значения. В упомянутой нами формализации понятия творящего субъекта, которое не было сформулировано Брауэром (его сформулируют лишь впоследствии другие математики), темпоральный аспект, характерный для интуиционизма, явно присутствует.
При всей важности аргументов, опирающихся на понятие творящего субъекта, для более глубокого понимания интуиционизма как философского подхода к математике их роль в развитии данного подхода была более скромной по сравнению с двумя актами интуиционизма, непосредственно приводящим к математическим истинам, принимаемых Брауэром и его последователями.
Математика
Хотя наработки Брауэра, развивающие идеи интуиционизма, сыграли важную роль в спорах вокруг кризиса оснований в начале XX века, далеко идущие следствия из его философии стали явными лишь спустя многие годы. Двумя наиболее характерными свойствами интуиционизма являются логические принципы рассуждения, допустимые в доказательствах, а также целостное представление интуиционистского континуума. Именно благодаря последнему интуиционизм оказывается несовместимым с классической математикой. В данной статье мы сосредоточимся на тех принципах интуиционизма, которые отличают его от прочих математических концепций, поэтому аспекты интуиционизма, разделяемые прочими конструктивистскими концепциями, будут рассматриваться здесь менее подробно.
Интерпретация БГК
С точки зрения интуиционизма, познание истинности высказывания А предполагает доказательство этого высказывания. В 1934 году Аренд Гейтинг, ученик Брауэра, представил схему того, что впоследствии стало известно как интерпретация Брауэра — Гейтинга — Колмагорова. БГК передает значение логических символов в контексте интуиционизма, а также в более широком контексте конструктивизма. БГК неформальным образом определяет, из чего должно состоять интуиционистское доказательство, за счет выявления того, как следует интерпретировать связки и кванторы.
⊥ не доказуемо.
● Доказательство

включает в себя доказательство А и доказательство В.
● Доказательство
A∨B
включает в себя доказательство А или доказательство В.
● Доказательство
A→B представляет собой построение, преобразующее всякое доказательство А в доказательство В.
● Доказательство

задается посредством введения элемента d, принадлежащего данной области, и доказательства А(d).
● Доказательство
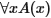
представляет собой построение, преобразующее всякое доказательство того, что d принадлежит данной области, в доказательство А(d).
Отрицание ¬A формулы А будет доказано, если мы сможем показать, что доказательства А не существует, то есть мы представим построение, в котором из всякого возможного доказательства А выводится противоречие. Таким образом, ¬A эквивалентно A→⊥. Интерпретация БГК не является формальным определением, поскольку понятие построения не определено, а следовательно, оно открыто для различных интерпретаций.
Согласно интерпретации БГК, это высказывание будет истинным с точки зрения интуиционизма, если творящему субъекту известно доказательство А или доказательство того, что А невозможно доказать. В случае, если нам неизвестно ни доказательство А, ни доказательство его отрицания, высказывание A∨¬A не будет истинным. Этот факт иллюстрируется наличием некоторых неразрешенных проблем, таких как проблема Гольдбаха или гипотеза Римана. Но как только мы нашли доказательство А или его отрицания, ситуация тут же изменяется, и с этого момента для данного конкретного А принцип A∨¬A уже будет выполняться
Интуиционистская логика
Брауэр отказывается от принципа исключенного третьего исходя из своей философской концепции, однако Аренд Гейтинг стал первым, кто сумел сформулировать последовательную логическую систему принципов, допустимых с точки зрения интуиционизма. Интуиционистскую логику, признаваемую также многими другими конструктивистскими концепциями, часто называют «классической логикой без принципа исключенного третьего». Она обозначается аббревиатурой ИИВ, которая расшифровывается как «Интуиционистское исчисление высказываний», впрочем, в литературе можно встретить и другие названия. Один из возможных способов гильбертовой аксиоматизации будет включать следующие принципы:
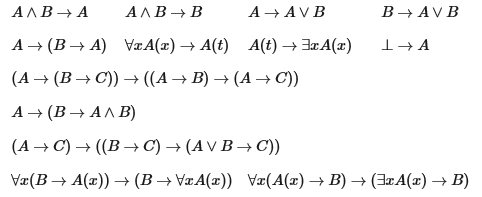
с обычными дополнительными условиями для двух последних аксиом и правилом modus ponens
(из А и (A→B) выводится В)
в качестве единственного правила вывода. Интуиционистская логика оставалась под пристальным вниманием исследователей с момента своего основания. Уже на уровне ее основных положений мы обнаруживаем множество свойств, отличающих ее от классической логики, например свойство дизъюнкции (DP):
(DP) ИИВ⊢A∨B влечет ИИВ⊢A или ИИВ⊢B.
Данный принцип явным образом нарушается в классической логике, так как в классической логике A∨¬A доказывается также для формул, независимых от логики, для которых как А, так и ¬A не являются тавтологиями. Исключение принципа «из ложного высказывания следует что угодно» (ex falso sequitur quodlibet: ⊥→A) в интуиционистской логике остается предметом обсуждений для исследователей, изучающих замечания Брауэра, связанные с этой проблемой; в работе van Atten 2008 утверждается, что данный принцип не выполняется в интуиционизме и что Брауэр принимает те же логические принципы, что принимаются в релевантной логике (более подробный анализ проблемы принципа ex falso sequitur quodlibet в интуиционизме Брауэра см. van Dalen 2004).
Хотя до сегодняшнего дня в интуиционизме применяется лишь логика, исчерпывающая ИИВ, вполне вероятно, что когда-нибудь будет введен принцип, который будет допустим, с точки зрения интуиционизма, но который не будет входить в ИИВ. Большинство конструктивистских концепций сходятся в том, что этого никогда не произойдет, полагая тем самым, что ИИВ является единственной логической системой, допустимой для конструктивизма. Для интуитивизма ситуация менее ясна, поскольку не исключено, что в какой-то момент наши интуиционистские представления могут привести нас к новым логическим принципам, которые мы не видели ранее.
Существует огромное множество систем доказательства для интуиционистской логики, например, исчисления Генцена и системы натурального вывода, а также различные формы семантики, такие как модели Крипке, модели Бета, алгебры Гейтинга, топологические семантики и категориальные модели. Некоторые из этих семантик, однако, представляют лишь классические средства изучения интуиционистской логики, ведь мы можем продемонстрировать невозможность существования интуиционистского доказательства их полноты (Kreisel 1962). Впрочем, было показано, что существуют альтернативные, хотя и чуть менее естественные модели, полные с конструктивистской точки зрения (Veldman 1976). Конструктивный характер интуиционистской логики становится особенно явным в контексте изоморфизма Карри — Говарда, который устанавливает соответствие между деривациями в логике и терминами в простом типизированном лямбда-исчислении, то есть между доказательствами и вычислениями. Соответствие сохраняет привычную структуру в том плане, что редукция терминов соответствует нормализации доказательств.
Натуральные числа
Существование натуральных чисел задается первым актом интуиционизма, то есть посредством восприятия движения времени и распадения жизненного момента на две отдельные составляющие: то, что было, 1, и то, что получается вместе с тем, что было, 2, а отсюда — 3, 4, … и т.д. В отличие от классической математики, в интуиционизме все бесконечные объекты рассматриваются как потенциально бесконечные. В частности, это касается бесконечного ряда натуральных чисел. Поэтому с высказываниями об элементах этого множества следует обращаться очень аккуратно. С другой стороны, принцип индукции, с точки зрения интуиционизма, считается безусловно приемлемым.
Вследствие конечности натурального числа, в отличие, скажем, от действительного числа, многие конечные по своей природе арифметические выражения, которые являются истинными в рамках классической математики, также будут истинными и в контексте интуиционизма. Например, в интуиционизме всякое натуральное число разлагается на простые множители; существуют перечислимые множества, которые невозможно вычислить; формула A∨¬A истинна для всякого высказывания А, не содержащего кванторы. Истинность более сложных высказываний, таких как теорема ван дер Вардена или теорема Крускала, в контексте интуиционизма не столь очевидна. В действительности интуиционистские доказательства обоих высказываний весьма сложны и сильно отличаются от соответствующих классических доказательств (Coquand 1995, Veldman 2004).
Таким образом, в контексте натуральных чисел интуиционизм и классическая математика разделяют много общих черт. Лишь когда речь идет о прочих бесконечных множествах, таких как множество действительных чисел, интуиционизм расходится с классической математикой, а также с большинством других конструктивистских теорий.
Континуум
С контексте интуиционизма континуум определяется одновременно и более широко, и более узко, нежели в классической математике. В своей полной форме оба понятия оказываются несовместимы, поскольку интуиционистские действительные числа обладают свойствами, которые классическая математика им не приписывает. Известным примером, который будет приведен ниже, является теорема, гласящая, что в интуиционизме всякая всюду определенная функция, заданная на континууме, будет непрерывной. Тот факт, что интуиционистский конинуум не удовлетворяет некоторым классическим свойствам, можно легко подтвердить посредством так называемых слабых контрпримеров. То, что он также обладает свойствами, которыми не обладают действительные числа в классической математике, следует из существования свободно становящихся последовательностей в интуиционизме.
Слабые контрпримеры
Слабые контрпримеры, введенные Брауэром в 1908 году, — это первые примеры, которые он использовал, чтобы показать, что переход от классического понимания математики к интуиционистскому не обойдется без последствий для математических истин, которые мы можем установить с соответствии с этими подходами. Эти примеры показывают, что некоторые классические положения на настоящий момент неприемлемы с точки зрения интуиционизма. К примеру, представим себе последовательность действительных чисел, заданную следующим определением:
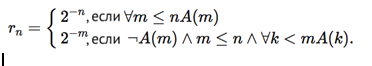
Здесь А(n) — разрешимое свойство, для которого мы не можем установить истинность или ложность высказывания ∀nA(n). Разрешимость означает, что на настоящий момент для всякого данного n существует (т.е. может быть построено) доказательство A(n) или его отрицания, ¬A(n). На момент написания этого текста мы могли бы, например, допустить, что А(n) выражает, что при n>2, n является суммой трех простых чисел; тогда ∀nA(n) будет выражать (исходную) проблему Гольдбаха, которая гласит, что всякое число больше 2 можно представить в виде суммы трех простых чисел.
Последовательность
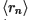
задает действительное число r, для которого выражение r=0 будет эквивалентно выражению ∀nA(n). Отсюда следует, что высказывание (r=0∨r≠0) не будет истинным, а следовательно, что закон трихотомии ∀x(x<y∨x=y∨x>y) не будет истинным для интуиционистского континуума.
Следует отметить тонкое различие между «А не интуиционистски истинно» и «А интуиционистски опровержимо»: в первом случае мы знаем, что для А не существует интуиционистского доказательства, в то время как во втором утверждении говорится, что мы располагаем доказательством ¬A, то есть построением, в котором из всякого возможного доказательства А следует противоречие. Для закона трихотомии, с точки зрения интуиционизма, как мы только что показали, это ложно. Далее мы покажем, что вторая сильная формулировка, которая гласит, что закон можно опровергнуть, будет интуиционистски истинной. Тем не менее это неистинно для всех тех высказываний, для которых существуют слабые контрпримеры. Например, проблема Гольдбаха представляет собой слабый контрпример к принципу исключенного третьего, поскольку, как было показано выше, на настоящий момент неизвестно, истинно или ложно выражение ∀nA(n), следовательно, в интуиционистской перспективе мы не можем утверждать истинность ∀nA(n)∨¬∀nA(n), во всяком случае на данный момент. Однако отрицание этого высказывания, ¬(∀nA(n)∨¬∀nA(n)), интуиционистски неистинно, поскольку для всякого высказывания В мы можем показать, что из утверждения истинности ¬B и ¬¬B выводится противоречие (а значит, — и из утверждения B&¬B). Иными словами, ¬¬(B∨¬B) истинно с точки зрения интуиционизма, а следовательно, хотя мы можем привести слабые контрпримеры к принципу исключенного третьего, его отрицание в интуиционизме будет ложным, то есть оно интуиционистски опровержимо.
Существование действительных чисел r, позитивность которых невозможно определить интуиционистски, показывает нам, что некоторые классические полные функции — например, кусочная постоянная функция
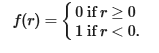
— перестают быть таковыми в интуиционистской перспективе.
Мы можем привести слабые контрпримеры ко многим истинным в классической математике высказываниям. Построение таких слабых контрпримеров зачастую проводится аналогично тому, как было показано в вышеприведенном примере. Так, аргумент, показывающий, что теорема о промежуточном значении неистинна, с точки зрения интуиционизма будет развиваться следующим образом.
Пусть r — действительное число в [-1,1], для которого, как в приведенном выше примере, не определено (r≤0∨0<r). Определим равномерно непрерывную функцию f на [0,3]: f(x)=min(x−1,0)+max(0,x−2)+r.
Очевидно, что f(0)=−1+r и f(3)=1+r, откуда f принимает значение 0 в некоторой точке х в промежутке [0,3]. Если такой х можно определить, то либо 1≤x, либо x≤2. Если f равно r на [1,2], в первом случае r≤0, а во втором 0≤r, что противоречит допущению о неразрешимости высказывания (r≤0∨0≤r).
Эти примеры, казалось бы, показывают, что при переходе от классической математики к интуиционистской мы должны отказаться от некоторых фундаментальных теорем. Однако это не так, поскольку во многих случаях интуиционизм реабилитирует такие теоремы в некоторой аналогичной форме, где высказывания о существовании замещаются на высказывания о существовании приближений при произвольно взятых ограничениях, как в следующем аналоге классической теоремы о промежуточном значении, который будет интуиционистски истинным:
Теорема. Для всякой непрерывной функции f с действительными значениями на интервале [a, b] при a<b и для всякого с между f(a) и f(b) будет верно
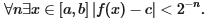
Слабые контрпримеры служат средством, с помощью которого мы можем показать, что определенные математические выражения не будут интуиционистски истинными, однако они не раскрывают богатства интуиционистского континуума. Лишь с введением идеи свободно становящихся последовательностей Брауэра интуиционизм приобрел свою исключительность, став несоизмеримым с классической математикой.
Свободно становящиеся последовательности
Идея свободно становящихся последовательностей была впервые сформулирована Брауэром, чтобы охарактеризовать интуицию континуума. Коль скоро для последователя интуиционизма всякая бесконечность является потенциальной, бесконечные объекты можно помыслить лишь в процессе их пошагового построения. Соответствующее построение, таким образом, должно определять, какие бесконечные объекты будут допустимы. Например, в большинстве прочих разновидностей конструктивизма допустимы лишь вычислимые правила построения таких объектов, в то время как в платонистической перспективе бесконечные объекты рассматриваются в качестве завершенных целостностей, существование которых допустимо даже тогда, когда нам неизвестны правила их построения.
Идея свободно становящихся последовательностей выводится из второго акта интуиционизма Брауэра. Так мы получаем некоторые бесконечные множества, обладающие свойствами, которые были бы недопустимы с точки зрения классической математики
Последовательность может быть задана посредством некоторого правила или алгоритма, например, как последовательность из одних нулей или простых чисел в порядке возрастания, и в таком случае мы говорим о последовательности, заданной законом; или же последовательность может не подчиняться какому-либо принципу, и тогда она будет называться беззаконной. Такую последовательность можно производить, скажем, бросая монетку или произвольно выбирая каждое следующее число данной последовательности. Таким образом, беззаконная последовательность всегда будет незавершенной, и единственная доступная информация о ней в каждый момент времени будет ограничиваться тем фрагментом этой последовательности, которая была образована на данный момент. Очевидно, что исходя из самой природы беззаконности мы никогда не сможем определить, совпадут ли ее значения со значениями последовательности, заданной законом. Кроме того, мы можем произвольно образовывать последовательности, начало которых выглядит закономерным, однако в какой-то момент закономерность исчезнет, и при записи последующих чисел в силу вступит свободный выбор, и наоборот.
Согласно Брауэру, всякое действительное число представлено свободно становящейся последовательностью; свободно становящиеся последовательности позволили ему изобразить интуиционистский континуум посредством противоречивых аксиом континуума. Свободно становящиеся последовательности впервые упоминаются в инаугурационном обращении Брауэра (Brouwer 1902), однако к тому времени он еще не рассматривал их в качестве фундаментальной составляющей математики. Постепенно они стали приобретать все большую важность; примерно с 1908 года Брауэр начинает использовать их так, как будет показано в следующем разделе.
Аксиомы непрерывности
Понятие свободно становящейся последовательности дает далеко идущие следствия. С точки зрения интуиционизма, оно служит обоснованием для использования аксиом непрерывности, из которых можно извлечь высказывания, не вписывающиеся в классическую математику. Наиболее слабой из этих аксиом является аксиома слабой непрерывности:
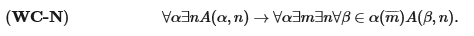
Здесь n и m пробегают множество натуральных чисел, α и β пробегают множество свободно становящихся последовательностей, а
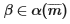
означает, что первые m элементов α и β равны. Хотя вплоть до настоящего момента никто — даже Брауэр — еще не сумел привести вполне удовлетворительного обоснования большинства аксиом непрерывности для произвольного образования последовательностей; при ограниченности классом «беззаконных» последовательностей аргументы в пользу пригодности аксиомы непрерывности выглядят следующим образом.
При каких условиях в интуиционистской математике возможно делать утверждение вида
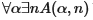
Согласно самой природе понятия беззаконной последовательности, выбор числа n, для которого А(α, n) будет истинно, должен осуществляться лишь тогда, когда нам уже известен конечный сегмент α. Ведь нам неизвестно, как α будет формироваться далее и, следовательно, мы будем основывать выбор n на начальном сегменте α, известном нам на момент времени, когда мы хотим установить n. Отсюда следует, что для всякой «беззаконной» последовательности β с таким же начальным сегментом, как и у α, A(β,n) также будет истинно.
Поскольку удалось доказать непротиворечивость слабой аксиомы непрерывности, она зачастую стала применяться в той форме, для которой можно привести обоснование, а именно в случае, в котором предикат А указывает лишь на значения α, а не на свойства более высокого порядка, которыми α, вероятно, обладает. Мы не будем приводить детали этого аргумента, однако скажем, что в нем содержатся те же элементы, что и в обосновании принципа беззаконных последовательностей (см. van Atten, van Dalen 2002).
Интуиционистские представления о континууме не исчерпываются понятием слабой непрерывности, поскольку в отношении данной аксиомы следует заключить, что выбор числа m такого, что
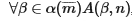
можно представить эксплицитно.
Так, из
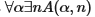
следует существование непрерывного функционала Ф, который для каждого α производит m, фиксирующий длину α на том основании, на котором избирается n. Выражаясь более формальным языком, пусть CF будет составлять класс непрерывных функционалов Ф, которые приписывают натуральные числа бесконечным последовательностям, то есть которые удовлетворяют условию
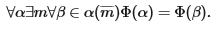
Полную аксиому непрерывности, которая представляет собой расширенную версию аксиомы слабой непрерывности, можно сформулировать следующим образом:
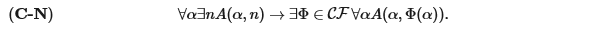
Посредством аксиомы непрерывности мы можем преобразовать некоторые слабые контрпримеры в полновесные опровержения принципов, принимаемых в классической математике. Например, из аксиомы непрерывности следует, что формулировка принципа исключенного третьего, в которой используется квантор всеобщности, является ложной:
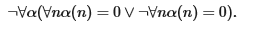
Здесь α(n) обозначает n-й элемент α.
Чтобы убедиться в корректности этого опровержения, предположим, отталкиваясь от противного, что ¬∀α(∀nα(n)=0∨¬∀nα(n)=0) истинно.
Из этого следует, что
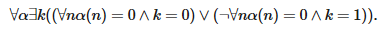
Согласно слабой аксиоме непрерывности, для α, состоящего из одних нулей, существует число m, фиксирующий выбор k, а это значит, что для всех
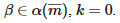
Однако существование последовательностей, первыми m элементами которых являются 0 и которые содержат 1, показывает нам, что это невозможно.
Рассмотрим, к примеру, действительное число ra, являющееся пределом последовательности, состоящей из чисел rn, как было показано в примере, представленном в разделе, посвященном слабым контрпримерам, где A(m), данное в определении, принимается за высказывание α(m)=0. Тогда из приведенного выше отрицания следует, что
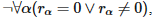
и следовательно, мы приходим к отрицанию закона трихотомии:
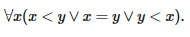
Следующая теорема представляет еще один пример того, как из аксиомы непрерывности можно извлечь опровержение некоторых принципов классической математики.
Теорема
(С-N) Всякая полная действительная функция является непрерывной.
Действительно, классический контрпример к этой теореме
f(x)={0, если х — рациональное число; 1, если х — иррациональное число}
недопустим с точки зрения интуиционизма, поскольку свойство «быть рациональным числом» неприменимо ко множеству действительных чисел. Из приведенной выше теоремы следует, что континуум нельзя разложить; в работе van Dalen 1997 было доказано, что это верно даже для множества иррациональных чисел.
Два вышеприведенных примера представляют весьма характерный способ применения аксиом непрерывности в интуиционистской математике; это единственные аксиомы в интуиционизме, не согласующиеся с классической моделью аргументации, поэтому они представляют наиболее яркий и вместе с тем наиболее противоречивый аспект философии Брауэра.
Функции окрестности
В литературе часто встречается соответствующая репрезентация непрерывных функционалов, однако Брауэр ее не использует. Непрерывные функционалы, приписывающие номера бесконечным последовательностям, можно представить посредством так называемых функций окрестности, где функция окрестности f — это функция на натуральных числах, удовлетворяющих следующим двум свойствам:
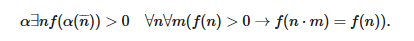
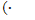
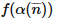
Интуитивно, если f репрезентирует Ф, то f(α(n¯))=0 значит, что α(n¯) недостаточно длинная, чтобы вычислить Φ(α), а f(α(n¯))=m+1 значит, что α(n¯) достаточно длинная, чтобы вычислить Φ(α), и что значением является m. Если К обозначает класс соседствующих функций, то мы можем переформулировать аксиому непрерывности C-N следующим образом:
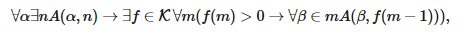
где
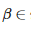
значит, что кодом начального сегмента β является m
Теорема о штрихе
Брауэр ввел понятие свободно становящихся последовательностей и аксиомы непрерывности для описания континуума в интуиционистской математике, однако одних этих принципов оказалось недостаточно для того, чтобы воспроизвести ту часть традиционного математического анализа, который Брауэр считал интуиционистски приемлемой, например, теорему, в которой утверждается, что всякая непрерывная действительная функция на замкнутом интервале является равномерно непрерывной. В связи с этим Брауэр принялся за доказательство так называемой теоремы о штрихе. В классической математике это утверждение считается истинным, однако многие полагают, что доказательство Брауэра и вовсе нельзя считать за доказательство, поскольку оно опирается на допущения относительно формы доказательств, в пользу которых не существует сколь-либо строгих аргументов. По данной причине теорему о штрихе иногда называют просто принципом штриха.
Наиболее известным следствием из теоремы о штрихе является так называемая теорема о веере, которая позволяет доказать упомянутую ранее теорему о равномерной непрерывности и которую мы рассмотрим сперва. Обе эти теоремы — как теорема о штрихе, так и теорема о веере — позволяют применять индукцию к некоторым фундированным множествам объектов, называемых потоками. Поток (spread) — аналог множества в интуиционистской математике, который передает идею бесконечного объекта как постоянно возрастающего и всегда незавершенного. Поток, по сути, представляет собой счетное разветвление, «пронумерованное» натуральными числами или другого рода конечными объектами и состоящее только из бесконечных линий.
Веер — это конечно ветвящийся поток; принцип веера выражает форму плотности, которая эквивалентна лемме Кёнига, классическое доказательство которой в интуиционистской математике недопустимо. Этот принцип гласит, что для всякого веера Т, каждая ветка которого в какой-то точке удовлетворяет свойству А, можно указать некоторую единообразную границу удовлетворения данного свойства. Такое свойство называется штрихом для Т.
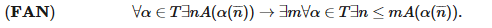
Здесь
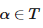
означает, что α является веткой Т. Принципа веера достаточно для доказательства теоремы, о которой мы говорили выше:
Теорема (FAN). Всякая непрерывная действительная функция на замкнутом интервале является равномерно непрерывной.
Брауэровское обоснование теоремы о веере опирается на принцип штриха для универсального потока:
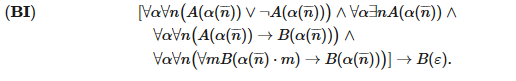
Здесь ε обозначает пустую последовательность, . обозначает конкатенацию, BI — индукцию штриха, D — разрешимость предиката А
Принцип штриха дает принцип индукции для деревьев в интуиционизме; он выражает принцип обоснованности для потоков относительно разрешимых свойств. Из работ Брауэра можно извлечь альтернативные формулировки этого принципа с менее строгими требованиями разрешимости, впрочем, мы не станем приводить их здесь. Формулировки принципа непрерывности и принципа штриха иногда объединяются в одну общую аксиому, называемую аксиомой непрерывности штриха.
Принцип штриха тесно связан с функциями окрестности, о которых шла речь в разделе, посвященном аксиомам непрерывности.
Пусть IK — индуктивно определенный класс функций окрестности, состоящих из всех констант ненулевых последовательностей λm.n+1, таких что если
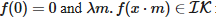
то
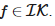
Утверждение К=IК, то есть утверждение, что функции окрестности можно производить индуктивным образом, эквивалентно
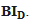
Брауэровскоге доказательство теоремы о штрихе примечательно тем, что в нем используются свойства вполне упорядоченности гипотетических доказательств. Оно основывается на допущении, что мы можем придать канонический (т.е. вполне упорядоченный) вид всякому доказательству, что некоторое свойство А, характеризующее последовательность, является штрихом. Хотя доказательство этого принципа, предложенное Брауэром, приемлемо с точки зрения классической математики, ясно, что его приемлемость в интуитивизме исходит из совершенно иного рода причин, нежели в классической математике.
Аксиомы выбора
Аксиома выбора в своей полной форме является недопустимой с точки зрения конструктивизма, по крайней мере при наличии некоторых других центральных аксиом теории множеств, таких как аксиома экстенсиональности (Diaconescu 1975). Пусть А будет высказыванием, истинность или ложность которого не установлена. Тогда принадлежность следующих двух множеств остается неразрешенной:
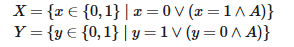
Существование функции выбора f:{X,Y}→{0,1}, выбирающей элемент из Х и Y, влечет (A∨¬A). Ведь если f(X)≠f(Y), отсюда вытекает X≠Y, а следовательно, ¬A, хотя f(X)=f(Y) влечет А. Следовательно, существование функции выбора для {X,Y} невозможно.
Тем не менее для этой аксиомы существуют некоторые ограничения, допустимые с точки зрения интуиционизма, например, аксиома счетного выбора, которую также принимают в качестве легитимного принципа некоторые «полуинтуиционисты», о которых пойдет речь ниже:
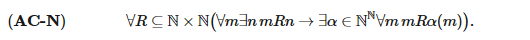
Данную схему можно обосновать следующим образом. Доказательство посылки должно указывать нам метод, который при наличии m дает число n, такое что mRn. Таким образом, мы можем произвести пошаговое построение функции α на множестве натуральных чисел N: сперва мы выбираем элемент m0, такой что 0Rm0, который будет значением α(0). Затем мы выбираем элемент m1, такой что 1Rm1, который будет значением α(1), и т.д.
Аналогичным образом можно привести обоснование некоторых других аксиом выбора. Здесь мы упомянем лишь еще одно такое доказательство — аксиому зависимого выбора:
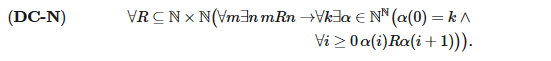
Кроме того, в классической математике с аксиомами выбора обращаются очень аккуратно и зачастую прямо указывают, сколько процедур выбора требуется в определенном доказательстве. Так как аксиома зависимого выбора совместима с важнейшими аксиомами классической теории множеств (аксиома детерминированности), в отличие от полной аксиомы выбора, этой аксиоме уделяется особое внимание, и в целом математики стремятся свести процедуры выбора, применяемые при доказательстве (если они и вовсе наличествуют), к зависимому выбору.
Дескриптивная теория множеств, топология и теория топосов
Брауэр не был единственным, кто выражал сомнения относительно некоторых классических моделей аргументации. Это в особенности заметно на примере дескриптивной теории множеств, которая возникла в качестве реакции на явно неконструктивные понятия, фигурирующие в канторовой теории множеств. Отцов-основателей этой теории, среди которых можно выделить Эмиля Бореля и Анри Лебега, называют полуинтуиционистами; предложенный ими конструктивный анализ континуума привел к определению иерархии Бореля. С их точки зрения, такое понятие как множество всех множеств действительных чисел, является бессмысленным, а следовательно, его следует заменить идею на иерархии подмножеств, не поддающейся четким определениям.
В работе Veldman 1999 был сформулирован интуиционистский аналог понятия борелева множества; Вельдман также показал, что из аналогов борелева множества, представленных в классической теории, выводится множество отдельных, с точки зрения интуиционизма, классов, — что нередко происходит в интуиционизме. Для «интуиционистских» борелевых множеств также будет выолняться аналог теоремы об иерархии Бореля. Доказательство этого факта во многом опирается на аксиомы непрерывности, о которых мы говорили ранее.
Еще один подход к изучению свойств подмножеств континуума (или топологического пространства вообще) появился в ходе развития формальной или абстрактной топологии (Fourman 1982, Martin-Löf 1970, Sambin 1987). В этой конструктивной топологии открытые множества и точки «меняются ролями». В классической топологии открытое множество определяется как некоторое множество точек; с другой стороны, в конструктивном сценарии открытое множество является фундаментальным понятием, через которое определяются точки. Поэтому данный подход иногда называют бесточечной топологией.
Интуиционистскую версию функционального анализа подробно и широко развивали последователи Брауэра, однако, поскольку многие подходы не укладываются в строгие рамки интуиционизма, но скорее вписываются в более широкий контекст конструктивизма, мы не станем рассматривать эту концепцию более подробным образом.
Конструктивизм
Интуиционизм разделяет некоторые основополагающие идеи прочих конструктивистских теорий. Конструктивизм в целом занимается конструктивными математическими объектами и доказательствами. Исходя из конструктивных доказательств мы можем (по крайней мере в принципе) вычленить алгоритмы вычисления элементов и воспроизвести построения, существование которых утверждается в доказательстве. Большинство форм конструктивизма совместимо с классической математикой, так как в основном они основываются на более строгой интерпретации и допустимых построениях, и при этом не вводятся никакие дополнительные допущения. Практически все конструктивистские теории основываются на одной и той же логической системе — на интуиционистской логике.
Для многих теорем о существовании в классической математике существуют аналоги в конструктивизме, в которых утверждение о существовании заменяется на утверждение о приближениях. Знакомым нам примером служит теорема промежуточного значения, о которой шла речь в разделе, посвященном слабым контрпримерам. Аналогичным образом мы можем представить конструктивистскую интерпретацию значительного числа разделов математики. Причина, по которой мы не будем останавливаться на них подробнее здесь, состоит в том, что в данной статье мы хотели бы сосредоточиться на тех аспектах интуиционизма, которые отличают его от прочих ветвей конструктивизма в математике (более тщательное рассмотрение идей конструктивизма читатель может найти в соответствующей статье, представленной в данной энциклопедии).
Метаматематика
Хотя Брауэр развивал свои идеи в совершенно конкретном и основательном ключе, их формализация в том виде, который известен нам сегодня, была проведена значительно позже другими математиками. Действительно, согласно позиции Брауэра, что математическое знание разворачивается неограниченным образом, его формализация (пусть и не недопустимая) отнюдь не является необходимой. Последующее поколение математиков рассуждали иначе, и проблема формализации интуиционистской математики, а также исследование ее метаматематических свойств, в особенности арифметики и математического анализа, привлекала многих исследователей. Выше мы уже приводили общую характеристику формализации интуиционистской логики, на которой основаны все прочие процедуры формализации.
Арифметика
Арифметика Гейтинга (НА) была создана Арендом Гейтингом в качестве формализации интуиционистской теории натуральных чисел (Heyting 1956). Она содержит те же нелогические аксиомы, что и в арифметике Пеано (РА), однако основывается на интуиционистской логике. Таким образом, она представляет собой более строгую версию классической арифметики, будучи общепринятой теорией натуральных чисел практически во всех разделах конструктивной математики. Арифметика Гейтинга обладает многими свойствами, отражающими ее конструктивный характер, например, свойством дизъюнкции, которое выполняется и в интуиционистской логике. Еще одним свойством арифметики Гейтинга, которое отсуствует в арифметике Пеано, является свойство нумерического существования: (n¯ нумерически соответствует натуральному числу n)
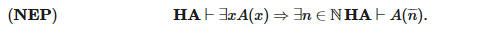
То, что это свойство отсутствует в PA, следует из факта, что в PA доказывается
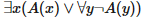
Представим, к примеру, случай, что А(х) — формула Т(е,е,х), где Т — разрешимый предикат Клини, выражающий, что х является кодом завершающего вычисления программы с кодом е при введении е. Если бы для каждого е существовало число n такое, что
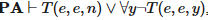
тогда проверив, истинно ли T(e,e,n), мы сможем решить, завершается ли программа е при введении е. Впрочем, в общем случае этот пример неразрешим.
Правило Маркова — это принцип, который выполняется как в классической, так и в интуиционистской математике, с той лишь разницей, что в HA доказательство этого факта будет нетривиальным:
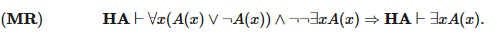
Так как в HA можно представить доказательство закона исключенного третьего для всякого примитивного рекурсивного предиката, то для такого А выводимость
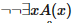
Из этого следует, что арифметика Пеано является
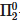
консервативной относительно арифметики Гейтинга. То есть для примитивного рекурсивного А мы получим:
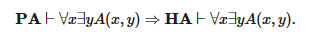
Таким образом, класс доказуемо рекурсивных функций арифметики Гейтинга совпадает с классом доказуемо рекурсивных функций арифметики Пеано — это свойство, которое отнюдь не будет неожиданностью исходя из основополагающих идей конструктивизма и интуиционизма.
Анализ
Формализация интуиционистской математики охватывает не только арифметику; была также аксиоматизирована значительная часть матанализа (Kleene 1965, Troelstra 1973). Конструктивный анализ этих систем можно провести, используя функциональную интерпретацию с точки зрения теории типов или выполнимости, большинство из этих интерпретаций основывается на так называемой диалектической интерпретации Гёделя (Gödel 1958, Kreisel 1959), выполнимости Клини (Kleene 1965) или теории типов (Martin-Löf 1984). В этих интерпретациях показаны различные способы эксплицирования функционалов, лежащих за конструктивными высказываниями, такие как функция, приписывающая у каждому х в
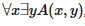
В работах Scott 1968, 1970 представлена топологическая модель для интуиционистской теории анализа второго порядка, где действительные числа интерпретируются как непрерывные функции из пространства Бэра в классические действительные числа. В этой модели выполняется схема Крипке, так же как и некоторые аксиомы непрерывности. В работе Moschovakis 1973 данный метод применяется для того, чтобы построить модель теорий интуиционистского анализа в терминах свободно становящихся последовательностей. В этой модели также выполняется схема Крипке и некоторые аксиомы непрерывности. В работе van Dalen 1978 модели Бета используются, чтобы задать модель арифметики и свободно становящихся последовательностей, которые удовлетворяют схеме выбора, примерам слабых континуумов и схеме Крипке. В этой модели областями на каждом узле являются натуральные числа, так что нам не пришлось бы использовать нестандартные модели, как в случае с моделями Крипке. Более того, в ней можно интерпретировать аксиомы творящего субъекта (CS1-3), что доказывает непротиворечивость данной теории.
Беззаконные последовательности
Предпринимались попытки аксиоматизировать беззаконные последовательности; все существующие аксиоматизации содержат расширенные аксиомы непрерывности (Kreisel 1968, Troelstra 1977), в частности в форме аксиомы открытых данных, которая гласит, что А(α) не содержит других не заданных законом параметров помимо α:
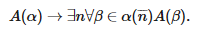
В работе Troelstra 1977 теория беззаконных последовательностей развивается (и обосновывается) в контексте интуиционистского анализа. Помимо аксиом для элементарного анализа там представлены усиленные формы аксиом открытых данных, непрерывности, разрешимости и плотности (аксиома плотности гласит, что всякая конечная последовательность является начальным сегментом беззаконной последовательности). Особенный интерес представляет тот факт, что в этих теориях можно устранить кванторы, задающие беззаконные последовательности; такой результат также можно расценивать в качестве задания модели заданных законом последовательностей для таких теорий. Другие классические модели теории беззаконных последовательностей выстраивались в теории категорий в виде моделей пучков (van der Hoeven and Moerdijk 1984). В работе Moschovakis 1986 представлена теория свободно становящихся последовательностей — наряду с классической моделью, в которой беззаконные последовательности оказываются как раз родовыми.
Формализация творящего субъекта
Творящий субъект, о котором шла речь в разделе 2.2, может производить свободно становящиеся последовательности — одни из наиболее важных и сложных объектов в интуиционистской математике Брауэра.
Темпоральный аспект понятия творящего субъекта формализуется при помощи записи □nA, которая обозначает, что в момент времени n творящий субъект располагает доказательством А (в некоторых других определениях это звучит так: истинность А в момент времени n). Георг Крайзель (Kreisel 1967) ввел следующие три аксиомы для творящего субъекта, совокупность которых обозначается как CS:

В версии Анны Троельстры (Troelstra 1969) последняя аксиома усиливается, принимая следующий вид:
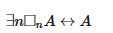
(творящий субъект доказывает лишь то, что является истинным; и то, что является истинным, в какой-то момент будет доказано творящим субъектом).
Первая аксиома CS1 не вызывает вопросов: мы можем в любой момент времени установить, располагает ли творящий субъект доказательством данного высказывания или нет. Вторая аксиома CS2 явно опирается на тот факт, что творящий субъект представляет собой идеализацию, поскольку она гласит, что доказательства никогда не забываются. Последняя аксиома CS3, вернее, вторая часть конъюнкции
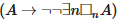
оказывается наиболее спорной частью формализации творческого субъекта; Крайзель назвал ее «аксиомой христианского милосердия». Йёран Сундхольм (Sundholm 2014), к примеру, утверждает, что аксиома христианского милосердия недопустима с точки зрения конструктивизма. А из теоремы Гёделя о неполноте и вовсе следует, что этот принцип является ложным, если мы предполагаем, что □nA будет доказуема в достаточно сильной системе доказательств, что, впрочем, отнюдь не совпадает с интерпретацией, которую подразумевал сам Брауэра.
Если в высказывании А не содержится никакого темпорального аспекта, то есть в нем не фигурирует □n, то мы можем определить свободно становящиеся последовательности сообразно следующему правилу (Brouwer 1953):
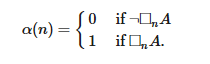
Отсюда следует, что представленный в разделе 2.2 принцип, который известен как схема Крипке (KS) и который отличается от аксиом, входящих в теорию творящего субъекта, не содержит явного темпорального аспекта:
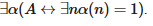
Опираясь на схему Крипке, мы можем формализовать слабые контрпримеры, не прибегая к идее творящего субъекта. Следующий пример взят из работы van Atten 2018. Пусть А — некоторое высказывание, и в настоящее время истинность выражения ¬A∨¬¬A не доказана. При помощи KS мы получим свободно становящиеся последовательности α1 и α2, такие что
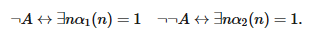
Поставим эти две последовательности в соответствие с действительными числами r0 и r1, где для i=0,1:
ri(n)={0, если αi(n)≠1; (-1)i2-m, если существуют m≤n, для которых истинно αi(m)=1, и ни для одного k<m не будет истинным αi(k)=1}.
Тогда для r=r0+r1 высказывание ¬A∨¬¬A выводится из (r>0∨r<0), а значит, r>0∨r<0 невозможно доказать.
В работе van Dalen 1978 выстраивается модель аксиом для творческого субъекта в контексте арифметики и свободно становящихся последовательностей, тем самым доказывая их совместимость с интуиционистской арифметикой и некоторыми разделами математического анализа. В van Dalen 1982 доказывается, что CS консервативны относительно арифметики Гейтинга. В van Dalen 1997 описываются математические следствия из схемы Крипке; ван Дален показывает, что KS и аксиомы непрерывности исключают принцип Маркова, в то время как из KS вкупе с принципом Маркова выводится принцип исключенного третьего.
Крипке сумел показать, что из KS следует существование нерекурсивных функций (впрочем, полученный результат был опубликован не им, а Крайзелем в Kreisel 1970). Очевидно, что отсюда следует, что теория CS также подразумевает существование нерекурсивной функции. Один из возможных аргументов в пользу CS будет выглядеть следующим образом. Допустим, что Х — невычислимое, но вычислимо перечислимое множество, тогда мы определим функцию f:

Тогда
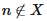
если и только если f(m,n)=1 при некотором натуральном значении m, откуда следует, что f не может быть вычислима. Если это так, то дополнение Х будет вычислимо перечислимым, откуда следует, что Х вычислимо. Коль скоро с точки зрения интуиционизма f является функцией, из этого следует, что в интуиционизме не все функции будут вычислимы.
Основания
Основой конструктивной математики служат формализации, которые относятся либо к теории множеств (Aczel 1978), либо к теории типов (Myhill 1975). Первые представляют собой адаптации теории множеств Цермело — Френкеля к конструктивистской перспективе, в то время как в теории типов построения, подразумеваемые в конструктивных высказываниях, эксплицируются в самой системе.
За последние года появилось множество моделей фрагментов такого рода теорий, служащих основанием для интуиционистской математики, некоторые из них мы упоминали выше. В частности, в теории топосов (van Oosten 2008) представлено множество моделей, описывающих некоторые характеристики интуиционизма. Например, существуют топосы, в которых все действительные всюду определенные функции являются непрерывными. Такие функциональные интерпретации, как реализуемость, так же как и интерпретации в теории типов, можно рассматривать в качестве моделей интуиционистской математики и большинства других конструктивистских теорий.
Обратная математика
Обратная математика занимается поиском аксиом, необходимых для доказательства математических теорем. В интуиционистской перспективе цель обратной математики остается такой же, но ограничивается интуиционистскими теоремами: если мы работаем над слабой интуиционистской теорией, аксиомы и теоремы совместимы друг с другом. Как правило, искомыми аксиомами, с которыми математики стремятся совместить теории, являются принцип веера, принцип штриха, схема Крипке и аксиомы непрерывности.
В работе Veldman 2011 исследуются аналоги принципа веера, соотнесенного с основополагающей теорией, называемой базовой интуиционистской математикой. Как было установлено, принцип веера эквивалентен утверждению, что единичный интервал [0,1] обладает свойством Гейне — Бореля, откуда выводится множество других эквивалентностей. В работе Veldman 2009 Вельдман показывает, что принцип веера равносилен также формулировке теоремы Брауэра о приблизительно неподвижной точке. В Lubarsky et al. 2012 обратная математика применяется для выведения схемы Крипке, которая оказывается эквивалентна некоторым положениям топологии.
Существует множество других примеров из интуиционистской обратной математики. В частности, в обширной области конструктивной обратной математики было достигнуто множество такого рода результатов, которые также будут релевантны, с точки зрения интуиционизма.
Философия
Брауэр, выстраивая свою интуиционистскую теорию с самого фундамента, высказывал крайне мало соображений по поводу связей интуиционизма с прочими существующими философскими концепциями математики, впрочем, вместо него это сделали его многочисленные последователи. В настоящем разделе мы осветим некоторые из отмеченных ими связей, в частности то, каким образом можно обосновать принципы интуиционизма исходя из прочих философских концепций.
Феноменология
Аналогию между интуиционизмом и феноменологией — философской концепцией, которую развивал Эдмунд Гуссерль — рассматривали несколько различных авторов, как еще при жизни Брауэра, так и после его смерти. Герман Вейль был одним из первых, кто обратил внимание на связь между идеями Брауэра и феноменологической трактовкой математики. Как и Брауэр, Вейль в своей книге «Континуум» (Das Kontinuum, гл. 2) говорит о так называемом интуиционистском континууме, однако понятие Вейля основывается на феноменологии (сознания) времени. Впоследствии Вейль приходит к выводу, что в своих наработках в области анализа действительных чисел Брауэр куда более верен идее интуиционистского континуума, нежели он сам (Weyl 1921), а посему молчаливо принимает позицию Брауэра, во всяком случае в отношении этого пункта (van Atten 2002).
Ван Аттен (van Atten 2003, 2007) опирается на феноменологию для того, чтобы обосновать статус свободно становящихся последовательностей в качестве математических объектов. Автор критикует обоснование, представленное Брауэром (van Atten 2002), что служит причиной поиска других способов обоснования. Понятие свободно становящихся последовательностей встречается в работах Беккера (Becker 1927) и Вейля, однако их определение отличается от брауэровского; Гуссерль же никогда публично не высказывался на эту тему. Ван Аттен объясняет, как гомогенность континуума обуславливает его неисчерпаемость и делимость — два ключевых свойства интуиционистского континуума по Брауэру. Отталкиваясь от того факта, что эти два существенных свойства фигурируют в определении свободно становящихся последовательностей, мы приходим к их феноменологическому обоснованию.
Виттгенштейн
10 марта 1928 года в Вене Брауэр прочитал лекцию, посвященную интуиционистским основниям математики. На этой лекции присутствовал Людвиг Витгенштейн, последовав совету Герберта Фейгля, который впоследствии писал о нескольких часах, проведенных после лекции с Витгенштейном и несколькими другими слушателями:
Некоторые исследователи спорят с тем, что лекция Брауэра оказала влияние на идеи Витгенштейна (Hacker 1986, Hintikka 1992, Marion 2003). Сложно сказать, в какой степени Брауэр повлиял на Витгенштейна (если такое влияние и вовсе имело место), однако в их позициях, безусловно, наблюдаются любопытные точки схождений и расхождений. Марион (Marion 2003) утверждает, что представления Витгенштейна о математике в том виде, в каком они были изложены в «Трактате», весьма близки к идеям Брауэра, и что Витгенштейн согласен с устранением принципа исключенного третьего (манускрипт 1929 года, Wittgenstein 1994: 155–156), однако он не согласен с аргументами Брауэра против этого принципа. Марион утверждает, что позиция Витгенштейна более радикальна, нежели позиция Брауэра.
Вельдман (Veldman 2019) рассматривает несколько пунктов сходств/различий между Брауэром и Витгенштейном, например, таких как угроза логики, которая, по мнению обоих, может привести к построениям без математического содержания. Одно из расхождений, о которых Вельдман упоминает в своей работе, связано с идеей Витгенштейна о том, что математика является коллективным предприятием, что резко противопоставляется идее творящего субъекта Брауэра и его убежденностью в том, что математика представляет собой неязыковую деятельность.
Даммит
Британский философ Майкл Даммит (Dummett 1973) разработал философский фундамент интуиционизма, в частности для интуиционистской логики. Даммит прямо утверждает, что его теория не сводится к истолкованию работы Брауэра, скорее, говоря его собственными словами, она представляет собой одну из возможных философских теорий, позволяющих «отвергнуть классические модели аргументации в математике в пользу интуиционистской модели».
Подход Даммита исходит из того, что выбор одной логической системы вместо другой необходимым образом должен опираться на значение, которое мы приписываем логическим высказываниям. В теории значения, используемой Даммитом, которая основывается на витгенштейновской концепции языка и, в частности, на его идее, что значение — это употребление, значение предложения определяется тем, как мы его употребляем. Значение математического выражения проявляется в том, как оно было употреблено, а понимание этого выражения — знание о том, как его можно употребить. Эта точка зрения подкрепляется тем, как мы получаем математическое знание. Изучая новое математическое понятие, мы, по сути, учимся тому, как его следует использовать: как его вычислять, доказывать, делать вывод, основываясь на нем, и т.д. И единственный способ установить, что мы верно поняли значение математического выражения, состоит в том, чтобы поверить наше умение правильно обращаться с данным выражением.
Как утверждает Даммит, это должно привести к тому, что мы примем интуиционистскую логику в качестве логической системы, применяемой в математических умозаключениях.
Любопытно, что, как отмечает сам Дамит (Dummett 1973), его теория значения весьма далеко отстоит от идеи Брауэра, что математика является принципиально неязыковой деятельностью. Таким образом, существуют по крайней мере две различные стратегии замещения классической логики на интуиционистскую — одна восходит к Брауэру, другая — к Даммиту. Труды Даммита по интуиционизму получили множество отзывов от различных философов, среди которых можно назвать Дага Правица (Prawitz 1977, 1986) и Рихарда Тизцена (Tieszen 1994, 2000).
Финитизм
Различные формы финитизма основываются на представлениях, аналогичных тем, что были сформулированы Даммитом, однако в них построения, используемые для доказательства математических выражений, должны существовать не только в принципе, но также и на практике. В зависимости от конкретной реализации последнего условия мы приходим к различным формам финитизма, таким как, например, ультраинтуиционизм Александра Есенина-Вольпина (Yessenin-Volpin 1970) или строгий финитизм Криспина Райта (Wright 1982).
Библиография
● Aczel, P., 1978, ‘The type-theoretic interpretation of constructive set theory,’ in Logic Colloquium ’77, A. Macintyre, L. Pacholski, J. Paris (eds.), North-Holland.
● van Atten, M., 2004, On Brouwer (Wadsworth Philosophers Series), Belmont: Wadsworth/Thomson Learning.
● –––, 2007, Brouwer meets Husserl (On the phenomenology of choice sequences), Dordrecht: Springer.
● –––, 2008, ‘On the hypothetical judgement in the history of intuitionistic logic,’ in Logic, Methodology, and philosophy of science XIII: Proceedings of the 2007 International Congress in Beijing, C. Glymour and W. Wang and D. Westerståhl (eds.), London: King’s College Publications.
● van Atten, M. and D. van Dalen, 2002, ‘Arguments for the continuity principle,’ Bulletin of Symbolic Logic, 8(3): 329–374.
● Beth, E.W., 1956, ‘Semantic construction of intuitionistic logic,’ KNAW Afd. Let. Med., Nieuwe serie, 19/11: 357–388.
● Brouwer, L.E.J., 1975, Collected works I, A. Heyting (ed.), Amsterdam: North-Holland.
● –––, 1976, Collected works II, H. Freudenthal (ed.), Amsterdam: North-Holland.
● –––, 1905, Leven, kunst en mystiek, Delft: Waltman.
● –––, 1907, Over de grondslagen der wiskunde, Ph.D. Thesis, University of Amsterdam, Department of Physics and Mathematics.
● –––, 1912, ‘Intuïtionisme en formalisme’, Inaugural address at the University of Amsterdam, 1912. Also in Wiskundig tijdschrift, 9, 1913.
● –––, 1925, ‘Zur Begründung der intuitionistischen Mathematik I,’ Mathematische Annalen, 93: 244–257.
● –––, 1925, ‘Zur Begründung der intuitionistischen Mathematik II,’ Mathematische Annalen, 95: 453–472.
● –––, 1948, ‘Essentially negative properties’, Indagationes Mathematicae, 10: 322–323.
● –––, 1952, ‘Historical background, principles and methods of intuitionism,’ South African Journal of Science, 49 (October-November): 139–146.
● –––, 1953, ‘Points and Spaces,’ Canadian Journal of Mathematics, 6: 1–17.
● –––, 1981, Brouwer’s Cambridge lectures on intuitionism, D. van Dalen (ed.), Cambridge: Cambridge University Press, Cambridge.
● –––, 1992, Intuitionismus, D. van Dalen (ed.), Mannhein: Wissenschaftsverlag.
● Brouwer, L.E.J. and C.S. Adama van Scheltema, 1984, Droeve snaar, vriend van mij – Brieven, D. van Dalen (ed.), Amsterdam: Uitgeverij de Arbeiderspers.
● Coquand, T., 1995, ‘A constructive topological proof of van der Waerden’s theorem,’ Journal of Pure and Applied Algebra, 105: 251–259.
● van Dalen, D., 1978, ‘An interpretation of intuitionistic analysis’, Annals of Mathematical Logic, 13: 1–43.
● –––, 1997, ‘How connected is the intuitionistic continuum?,’ Journal of Symbolic Logic, 62(4): 1147–1150.
● –––, 1999/2005, Mystic, geometer and intuitionist, Volumes I (1999) and II (2005), Oxford: Clarendon Press.
● –––, 2001, L.E.J. Brouwer (een biografie), Amsterdam: Uitgeverij Bert Bakker.
● –––, 2004, ‘Kolmogorov and Brouwer on constructive implication and the Ex Falso rule’ Russian Math Surveys, 59: 247–257.
● van Dalen, D. (ed.), 2001, L.E.J. Brouwer en de grondslagen van de wiskunde, Utrecht: Epsilon Uitgaven.
● Diaconescu, R., 1975, ‘Axiom of choice and complementation,’ in Proceedings of the American Mathematical Society, 51: 176–178.
● Fourman, M., and R. Grayson, 1982, ‘Formal spaces,’ in The L.E.J. Brouwer centenary symposium, A.S. Troelstra and D. van Dalen (eds.), Amsterdam: North-Holland.
● Gentzen, G., 1934, ‘Untersuchungen über das logische Schließen I, II,’ Mathematische Zeitschrift, 39: 176–210, 405–431.
● Gödel, K., 1958, ‘Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes,’ Dialectia, 12: 280–287.
● Hacker, P. M. S., 1986, Insight & Illusion. Themes in the Philosophy of Wittgenstein, revised edition, Clarendon Press, Oxford.
● Heyting, A., 1930, ‘Die formalen Regeln der intuitionistischen Logik,’ Sitzungsberichte der Preussischen Akademie von Wissenschaften. Physikalisch-mathematische Klasse, 42–56.
● –––, 1956, Intuitionism, an introduction, Amsterdam: North-Holland.
● van der Hoeven, G., and I. Moerdijk, 1984, ‘Sheaf models for choice sequences,’ Annals of Pure and Applied Logic, 27: 63–107.
● Kleene, S.C., and R.E. Vesley, 1965, The foundations of intuitionistic mathematics, Amsterdam: North-Holland.
● Koetsier, T., 2019, ‘Wittgenstein and Brouwer’s 1928 Lecture in Vienna: The Spirit of Schopenhauer’. To appear.
● Kreisel, G., 1959, ‘Interpretation of analysis by means of constructive functionals of finite type,’ in Constructivity in mathematics, A. Heyting (ed.), Amsterdam: North-Holland.
● –––, 1962, ‘On weak completeness of intuitionistic predicate logic,’ Journal of Symbolic Logic, 27: 139–158.
● –––, 1968, ‘Lawless sequences of natural numbers,’ Compositio Mathematica, 20: 222–248.
● Kripke, S.A., 1965, ‘Semantical analysis of intuitionistic logic’, in Formal systems and recursive functions, J. Crossley and M. Dummett (eds.), Amsterdam: North-Holland.
● Lubarsky, R., F. Richman, and P. Schuster 2012, ‘The Kripke schema in metric topology’, Mathematical Logic Quarterly, 58(6): 498–501.
● Maietti, M.E., and G. Sambin, 2007, ‘Toward a minimalist foundation for constructive mathematics,’ in From sets and types to topology and analysis: toward a minimalist foundation for constructive mathematics, L. Crosilla and P. Schuster (eds.), Oxford: Oxford University Press.
● Marion, M., 2003, ‘Wittgenstein and Brouwer’, Synthese 137: 103–127.
● Martin-Löf, P., 1970, Notes on constructive mathematics, Stockholm: Almqvist & Wiskell.
● –––, 1984, Intuitionistic type theory, Napoli: Bibliopolis.
● Moschovakis, J.R., 1973, ‘A topological interpretation of second-order intuitionistic arithmetic,’ Compositio Mathematica, 26(3): 261–275.
● –––, 1986, ‘Relative lawlessness in intuitionistic analysis,’ Journal of Symbolic Logic, 52(1): 68–87.
● Myhill, J., 1975, ‘Constructive set theory,’ Journal of Symbolic Logic, 40: 347–382.
● Niekus, J., 2010,‘Brouwer’s incomplete objects’ History and Philosophy of Logic 31: 31–46.
● van Oosten, J., 2008, Realizability: An introduction to its categorical side, (Studies in Logic and the Foundations of Mathematics: Volume 152), Amsterdam: Elsevier.
● Sambin, G., 1987, ‘Intuitionistic formal spaces,’ in Mathematical Logic and its Applications, D. Skordev (ed.), New York: Plenum.
● Scott, D., 1968, ‘Extending the topological interpretation to intuitionistic analysis,’ Compositio Mathematica, 20: 194–210.
● –––, 1970, ‘Extending the topological interpretation to intuitionistic analysis II’, in Intuitionism and proof theory, J. Myhill, A. Kino, and R. Vesley (eds.), Amsterdam: North-Holland.
● Sundholm, B.G., “Constructive Recursive Functions, Church's Thesis, and Brouwer's Theory of the Creating Subject: Afterthoughts on a Paris Joint Session”, in Jacque Dubucs & Michel Bordeau (eds.), Constructivity and Computability in Historical and Philosophical Perspective, Logic, Epistemology, and the Unity of Science no. 34, pp. 1–35, Dordrecht: Springer.
● Tarski, A., 1938, ‘Der Aussagenkalkül und die Topologie,’ Fundamenta Mathematicae, 31: 103–134.
● Troelstra, A.S., 1973, Metamathematical investigations of intuitionistic arithmetic and analysis, (Lecture Notes in Mathematics: Volume 344), Berlin: Springer.
● –––, 1977, Choice sequences (Oxford Logic Guides), Oxford: Clarendon Press.
● Troelstra, A.S., and D. van Dalen, 1988, Constructivism I and II, Amsterdam: North-Holland.
● Veldman, W., 1976, ‘An intuitionistic completeness theorem for intuitionistic predicate logic,’ Journal of Symbolic Logic, 41(1): 159–166.
● –––, 1999, ‘The Borel hierarchy and the projective hierarchy in intuitionistic mathematics,’ Report Number 0103, Department of Mathematics, University of Nijmegen. [available online]
● –––, 2004, ‘An intuitionistic proof of Kruskal’s theorem,’ Archive for Mathematical Logic, 43(2): 215–264.
● –––, 2009, ‘Brouwer’s Approximate Fixed-Point Theorem is Equivalent to Brouwer’s Fan Theorem,’ in Logicism, Intuitionism, and Formalism – Synthese Library 341, S. Lindström, E. Palmgren, K. Segerberg, V. Stoltenberg-Hansen (eds.): 277–299.
● –––, 2014, ‘Brouwer’s Fan Theorem as an axiom and as a contrast to Kleene’s Alternative,’ in Archive for Mathematical Logic 53 (5–6): 621–693.
● –––, 2019, ‘Intuitionism is all bosh, entirely. Unless it is an inspiration.’ To appear.
● Weyl, H., 1921, ‘Über die neue Grundlagenkrise der Mathematik,’ Mathematische Zeitschrift, 10: 39–70.
● Wittgenstein, L., 1994, Wiener Ausgabe, Band 1, Philosophische Bemerkungen, Springer Verlag, Wien/New York.
● Wright, C., 1982, ‘Strict Finitism’, Synthese 51 (2): 203–282.
● Yessenin-Volpin, A.S., 1970, ‘The ultra–intuitionistic criticism and the antitraditional program for foundations of mathematics’, in Intuitionism and Proof Theory, A. Kino, J. Myhill, and R. Vesley (eds.), North-Holland Publishing Company: Amsterdam, London: 3–45.