философы

Поделиться статьей в социальных сетях:

в избранное

Ян Лукасевич

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 15 мая 2014 года; содержательно преобразовано 6 июня 2014 года.

Ян Лукасевич (1878–1956) — польский логик и философ, который положил начало математической логике в Польше и стал одним из основателей, устроителей и учителей Варшавской школы логики. Его наиболее известным достижением стала первая строгая формулировка многозначной логики. Он предложил много улучшений в пропозициональной логике и стал первым историком логики, который рассматривал ее историю с позиции современной формальной логики.

Жизнь

Жизнь Яна Лукасевича — карьера ученого и академика, серьезно подорванная военными потрясениями XX века. Он родился и получил образование в польской Австрии, достиг своего расцвета во Второй Польской Республике, перенес тяготы войны, бежал от Красной армии в Германию и нашел последнее пристанище в Ирландии.

Ян Леопольд Лукасевич родился 21 декабря 1878 года во Львове [1], исторически польском городе, в то время бывшим столицей австрийской Галиции. Отец Лукасевича Павел был капитаном австрийской армии, его мать Леопольдина, урожденная Хольцер, была дочерью австрийского государственного служащего. Ян был их единственным ребенком. Семья говорила по-польски. Лукасевич посещал школу (классическую Gimnazjum, или гимназию с акцентом на классические языки) с 1890 года, закончил ее в 1897 году и начал изучать право во Львовском университете. При австрийском правлении университет разрешал преподавание на польском языке. В 1898 году Лукасевич переключился на математику, учась у Юзефа Пузыны, и философию, учась у Казимира Твардовского, который был назначен там экстраординарным профессором в 1895 году, а также у Войцеха Дзедушицкого. В 1902 году Лукасевич получил докторскую степень по философии за диссертацию «Об индукции как обратной дедукции» под руководством Твардовского. Получив только высшие оценки на всех экзаменах между выпускными экзаменами и диссертацией, он был награжден докторской степенью sub auspiciis Imperatoris — редким отличием — и получил бриллиантовое кольцо от императора Франца-Иосифа.

С 1902 года Лукасевич работал частным преподавателем и служащим в университетской библиотеке. В 1904 году он получил стипендию от автономного правительства Галиции и отправился учиться в Берлин, затем в Лёвен. В 1906 году он защитил свою габилитационную работу «Анализ и построение понятия причины». Как приват-доцент философии, он мог давать лекции в университете, став первым коллегой Твардовского из его студентов. Его первый курс лекций, прочитанный осенью 1906 года, был посвящен алгебре логики в формулировке Кутюра. В 1908 и 1909 годах он получил стипендию, которая позволила ему посетить Грац, где он познакомился с Алексиусом Мейнонгом и его школой. В 1911 году Лукасевич был назначен экстраординарным профессором и продолжал преподавать во Львове до начала войны в 1914 году. В это время среди его учеников были Казимеж Айдукевич и Тадеуш Котарбинский, которые впоследствии сами стали знаменитыми философами. Также в 1912 году он познакомился со Станиславом Лесьневским, который, однако, не может считаться его учеником, поскольку приехал во Львов после учебы за границей.

В 1915 году в результате войны Варшава оказалась под контролем Германии, и было решено вновь открыть университет, который бы не функционировал как польскоязычный университет при российском правлении. Лукасевич стал там профессором философии. В 1916 году он стал деканом факультета искусств, а в 1917 году — проректором университета. В 1918 году Лукасевич покинул университет, будучи назначен начальником отдела высших школ в новом польском Министерстве образования, а после того, как Польша получила полную независимость, стал министром образования в кабинете Падеревского с января по декабрь 1919 года. С 1920 по 1939 год он, как и Лесьневский, был профессором факультета естественных наук Варшавского университета. В 1922–1923 и снова в 1931–1932 годах он занимал пост ректора университета. В 1929 году он женился на Регине Барвиньской.

Он подружился с единственным немецким профессором математической логики Генрихом Шольцем и в 1938 году получил почетную докторскую степень в Мюнстерском университете. В этот период он также стал Великим Командором ордена Polonia Restituta (1923), Великим Командором Венгерского Ордена Заслуг, удостоился денежной премии от города Варшавы (1935) и членства в Польской академии искусств и наук в Кракове и Польских научных обществах во Львове и Варшаве.

Студентами, чьими докторскими диссертациями он руководил, были: Мордехай Вайсберг, Зигмунт Кобржинский, Станислав Яшковский, Болеслав Собочинский и Ежи Слупецкий.

В начале войны в сентябре 1939 года дом Лукасевичей был разбомблен Люфтваффе: все его книги, бумаги и корреспонденция были уничтожены за исключением одного тома переплетенных отпечатков. Лукасевичи жили во временном размещении для научных работников. Немецкие оккупанты закрыли университет, и Лукасевич нашел работу за скудную зарплату в варшавском городском архиве. Дополнительную финансовую поддержку оказал Шольц. Лукасевич преподавал в подпольном университете. С конца 1943 года, опасаясь неминуемого прихода и оккупации Польши Красной армией, а также находясь под подозрением у некоторых коллег в прогерманских и антиеврейских настроениях, Лукасевич выразил Шольцу желание покинуть Польшу вместе со своей женой. В качестве первого шага к их поездке в Швейцарию Шольцу удалось получить разрешение на поездку Лукасевичей в Мюнстер. Они покинули Варшаву 17 июля 1944 года, всего за две недели до начала Варшавского восстания. После заговора против Гитлера 20 июля 1944 года у них не было никакой надежды получить разрешение на выезд в Швейцарию. Они оставались в Мюнстере, терпя бомбардировки союзников, до января 1945 года, когда Юрген фон Кемпски предложил им жилье на своей ферме в Хембсене (Крайс-Хёкстер, Вестфалия), где они были освобождены американскими войсками 4 апреля.

С лета 1945 года Лукасевич преподавал логику в польской средней школе, расположенной в бывшем польском лагере для военнопленных в Дёселе. В октябре 1945 года его семье разрешили поехать в Брюссель. Там Лукасевич снова преподавал логику во временном Польском научном институте. Не желая возвращаться в Польшу, находящуюся под коммунистическим контролем, Лукасевич искал работу в другом месте. В феврале 1946 года он получил предложение поехать в Ирландию. 4 марта 1946 года Лукасевичи прибыли в Дублин, где их приняли министр иностранных дел и премьер-министр Имон де Валера. Осенью 1946 года Лукасевич был назначен профессором математической логики в Ирландской королевской академии (RIA), где он читал лекции сначала один, а затем два раза в неделю.

В последние годы жизни в Ирландии Лукасевич возобновил контакты с зарубежными коллегами, в частности с Шольцем, с которым постоянно переписывался. Он посещал конференции в Великобритании, Франции и Бельгии, отправлял статьи в Польшу, прежде чем был исключен (вместе с 15 другими беглыми поляками) из Польской академии в Кракове, читал лекции по математической логике в Университете Квинс в Белфасте и по силлогистике Аристотеля в Университетском колледже Дублина. Его здоровье ухудшилось, и он перенес несколько сердечных приступов: к 1953 году он больше не мог читать лекции в Академии. В 1955 году он получил почетную докторскую степень в Дублинском Тринити-колледже. 13 февраля 1956 года, после операции по удалению желчных камней, он перенес третий крупный коронарный тромбоз и умер в больнице. Он был похоронен на кладбище Гласневин в Дублине, «вдали от дорогого Львова и Польши», как гласит его надгробие. Регина сдала на хранение большую часть его научных работ и корреспонденции в RIA. В 1963 году Академия передала свои фонды в библиотеку Манчестерского университета, где они и остались, не внесенные в каталог. Выбор Манчестера был обусловлен присутствием там в качестве лектора Чеслава Леевского, который учился у Лукасевича в Варшаве и дважды отдавал ему на проверку докторскую диссертацию — один раз в 1939 году, когда помешала война, второй раз в Лондоне в 1954 году. Именно вторую редакцию книги Лукасевича о силлогистике Аристотеля Леевский подготовил к печати: она вышла посмертно в 1957 году.

Влияние Твардовского

Лукасевич был одним из первых учеников Твардовского во Львове, и на его взгляды и методы повлиял его учитель. Твардовский родился и учился в Вене, где стал учеником Франца Брентано и проникся его идеей философии как строгой дисциплины, которую следует исследовать с такой же тщательностью и вниманием к деталям, как и любую эмпирическую науку, и сообщать с предельной прозрачностью. В 1895 году Твардовский был назначен экстраординарным профессором во Львове. Он находил польскую философскую жизнь вялой и третьесортной и приступил к оживлению предмета и построению польских институтов за счет собственной академической работы. Как и Брентано, он считал, что обоснованная описательная психология является методологической основой философии, и, как и Брентано, он выступал за то, чтобы внести небольшие изменения в формальную логику. Лукасевич под влиянием Гуссерля, Рассела и Фреге отверг идею об основополагающей роли психологии и, в частности вдохновленный двумя последними, реформировал логику серьезнее, чем ожидал Твардовский. Лесьневский прочитал «Принципы математики» Рассела в 1904 году, и книга оказала на него значительное влияние. Лукасевич перенял общую идею о том, что философия может и должна стремиться быть научно точной, хотя оценивал состояние предмета скорее пессимистически, и выступал за фундаментальное реформирование философии в логическом направлении.

Еще одним аспектом, в котором Лукасевич продолжал традицию школы Брентано, было его уважение к истории философии, особенно к Аристотелю и британским эмпирикам. (Он и Твардовский перевели первое «Исследование…» Юма на польский.) Твардовский, хорошо знавший работы Больцано, указывал на сходство между понятиями теории вероятности Больцано и Лукасевича. Уважение к истории также лежало в основе новаторских исследований Лукасевича в истории логики, в частности стоической пропозициональной логики и силлогистики Аристотеля.

Лукасевич подражал Твардовскому и даже превосходил его в своем внимании к ясности выражения. Квалифицированные специалисты сходятся во мнении, что научная проза Лукасевича, на каком бы из трех языков он ни писал, отличается непревзойденной ясностью и красотой.

Ранние труды

В годы, предшествовавшие Первой мировой войне, Лукасевич занимался преимущественно вопросами методологии науки. Его докторская диссертация «Об индукции как обратной дедукции», опубликованная в 1903 году, исследовала связь между двумя разновидностями умозаключения в свете работ Джевонса, Зигварта и Эрдмана. Индуктивное рассуждение, исходящее из единичных эмпирических утверждений, пытается, согласно его раннему пониманию, прийти к общему заключению, которому можно приписать определенную вероятность. Вскоре же Лукасевич перешел к мнению, что нельзя приписать определенную вероятность общему утверждению на основе индукции — метод эмпирических наук состоит в том, чтобы творчески рискнуть мыслью, что определенное обобщение истинно, вывести из него единичные выводы и затем посмотреть, истинны ли они. Если хотя бы один из выводов не является истинным, то общее утверждение опровергается. Эта ранняя формулировка гипотетико-дедуктивного метода науки предвосхищает идеи Поппера более чем на два десятилетия, хотя и выражена менее убедительно. Лукасевич также предвосхитил Поппера, выдвинув «творческие элементы в науке» на передний план, выступив против идеи, что задача ученого — воспроизводить или воспроизводить факты.

Интерес к теории вероятностей лежал в основе одной из двух монографий Лукасевича, опубликованных до войны, а именно в «Логических основах теории вероятностей», написанной и опубликована не на польском, а на немецком языке. В 1908 и 1909 годах Лукасевич посетил Грац, где Алексиус Мейнонг и Эрнст Малли также работали над теорией вероятностей, поэтому вполне вероятно, что книга была написана на немецком языке, потому что их языком обсуждения был немецкий, а также для того, чтобы обеспечить более широкую аудиторию. Теория Лукасевича конструктивно использует идеи, почерпнутые из других источников: у Фреге он взял идею истинностного значения, у Уайтхеда и Рассела — идею неопределенной пропозиции, а у Больцано — идею отношения истинных значений ко всем значениям пропозиции. Рассмотрим классический пример урны, где урна содержит m черных шаров и n белых шаров. Пусть неопределенная пропозиция «x — черный шар в этой урне» таково, что переменная «x» может принимать в качестве значения любое выражение, называющее шар в урне. Тогда говорят, что область допустимых значений переменной — отдельные шары, а различные выражения, называющие один и тот же шар, имеют одно и то же значение. (Обратите внимание, что Лукасевич обращается к терминологии, которую позже будут ассоциировать с Куайном, говоря о переменной, принимающей значения — здесь выражения — с областью допустимых значений, соответствующей объектам, обозначенным этими выражениями.) Неопределенная пропозиция считается истинной, если она дает истинную пропозицию (Лукасевич называет определенную пропозицию «суждением») для всех значений его переменных; ложной, если дает ложную пропозицию для всех значений; или же ни истинной, ни ложной, если дает истинные суждения для одних значений и ложные суждения для других. Соотношение истинных значений и всех значений Лукасевич затем назовет значением неопределенной пропозиции. Для истинных неопределенностей это 1, для ложных неопределенностей это 0, а для других это рациональное число между 0 и 1 (рациональное, потому что рассматриваются только конечные области). В нашем случае истинностное значение неопределенного предложения «x — черный шар в этой урне» — mm+n.

На этой основе Лукасевич развивает исчисление истинностных значений, в котором можно работать с логически сложными пропозициями, условной вероятностью, вероятностной независимостью и выводить теорему Байеса. Исчисление истинностных значений используется как логическая теория вероятностей, помогающая работать с определенной реальностью: Лукасевич отрицает, что может существовать теория объективной или субъективной вероятности как таковой. Две идеи из этой короткой, но замечательной работы заслуживают особого внимания, поскольку они перекликаются с более поздними идеями Лукасевича. Во-первых, идея пропозиции (в данном случае неопределенной пропозиции), не являющейся ни истинной, ни ложной; во-вторых, связанная с этим идея о том, что такая пропозиция имеет числовое значение истинности между 0 (ложь) и 1 (истина). Теория Лукасевича заслуживает большей известности: она продолжает и расширяет более ранние идеи Больцано — вероятность у Лукасевича соответствует степени обоснованности пропозиции (относительно переменных составляющих) у Больцано. Ее главный недостаток заключается в том, что она сформулирована только для конечных областей.

Из всех работ Лукасевича, опубликованных до Первой мировой войны, одна наиболее ясно предвосхитила его более поздние опасения. Это была монография 1910 года «О принципе противоречия у Аристотеля». Она стала решающим поворотным пунктом в развитии Львовско-Варшавской школы. Это была первая работа, в которой Лукасевич развернуто поставил под вопрос допущения традиционной аристотелевской логики.

Лукасевич представляет проект своей монографии — критического исследования легитимности принципа противоречия, по-разному сформулированного Аристотелем — в контексте его критики Гегелем и возможности пересмотра в свете развития математической логики от Буля до Рассела. Источники Лукасевича для постгегельянского обсуждения «логического вопроса» — это Уэбервег, Тренделенбург и Зигварт. Более локальным контекстом было, вероятно, представление Твардовского об абсолютной и вневременной природе истины.

Онтологическая: не существует объекта, который может одновременно обладать и не обладать некоторым свойством.

Логическая: Противоречивые утверждения не могут быть одновременно истинными.

Психологическая: Никто не может одновременно верить в противоречащие друг другу вещи.

Лукасевич критикует Аристотеля за то, что он, с одной стороны, утверждает, что принцип противоречия не может быть доказан, а с другой — пытается найти его косвенное или прагматическое «доказательство». В частичном согласии с традицией, в соответствии с которой принцип противоречия не является краеугольным камнем или основным принципом логики, Лукасевич утверждает, что его статус менее надежен, чем статус некоторых других логических утверждений, и что его функция состоит главным образом в том, чтобы служить прагматической нормой. Тем не менее в приложении к книге он дает формальный вывод одной версии принципа противоречия из других принципов. Он показывает, что принцип противоречия — всего лишь одна логическая теорема среди других. Сегодня это утверждение вызвало бы мало удивления, но было довольно радикальным в свое время. Среди допущений, используемых при выводе, есть версия принципа двузначности, согласно которой каждая пропозиция либо истинна, либо ложна, и ни одна из них не является и той, и другой, так что вывод принципа противоречия, в конце концов, не является таким уж неожиданным.

Позже Лукасевич говорил, что в монографии пытался разработать разработать «неаристотелевскую логику», но признал, что ему это не удалось — главным образом потому, что на этом этапе он не был готов отвергнуть принцип двузначности. Вполне возможно, что из-за влияния Мейнонга Лукасевич приходит к тому, чтобы дать свои естественноязыковые интерпретации символизма алгебры логики Кутюра в приложении. От пропозициональной логики, которую Лукасевич должен был сделать в значительной степени своей собственной, почти не осталось и следа: интерпретации неуклюже теоретико-объектны — константа «0», например, которая может быть естественно истолкована как постоянно ложная пропозиция (и это происходит в более поздних работах Лукасевича), представлена как «объект, который не существует». Это одна из причин, по которой формальная работа Лукасевича в приложении к монографии 1910 года выглядит относительно архаичной. В то время как переменные буквы, такие как a, b и т.д., «означают утвердительные предложения», а их отрицания a′, b′ и т.д. «означают отрицательные предложения», и на практике они работают как пропозициональные переменные и их отрицания в современной пропозициональной логике, Лукасевич дает им гибридную интерпретацию: «a» передается как «X содержит a», а «a′» как «X не содержит a», в то время как «1» означает, что X является объектом, а «0» ― что X не является объектом. Это достаточно запутанно и не является классической сентенциальной логикой намеренно, даже если работает так на практике.

Хотя сама по себе книга имела успеха, она показывает Лукасевича на пороге его более поздних логических прорывов. Молодой Лесьневский прочитал ее в 1911 году и попытался, вопреки идеям Лукасевича, доказать принцип противоречия. В 1912 году он появился на пороге дома Лукасевича со словами: «Я ― Лесьневский, и я пришел показать вам доказательства из статьи, которую я написал против вас». Книга способствовала дальнейшей дискуссии во Львове: Котарбинский писал в защиту идеи Аристотеля, о которой размышлял Лукасевич, что утверждение о будущих случайных событиях может не иметь истинностного значения до события и приобретает его только после. Лесьневский отстаивал противоположное и убедил Котарбинского в своей позиции (согласующейся с более ранними взглядами Твардовского и более поздними взглядами Тарского), что истина вневременна или, как выражался Лесьневский, вечна и вечноживуща. Лукасевич вскоре принял более раннюю точку зрения Котарбинского и тем самым сделал свое самое знаменитое открытие — открытие многозначной логики.

Пропозициональная логика

Открытия в пропозициональной логике

Лукасевич столкнулся с пропозициональной логикой, которую он первоначально, вслед за Уайтхедом и Расселом, назвал «теорией дедукции», в работах Уайтхеда, Рассела и Фреге. В 1921 году Лукасевич опубликовал статью «Двузначная логика», в которой он свел воедино результаты в алгебре логики, управляющей двумя истинностными значениями истинного и ложного, которые, как и Фреге, Лукасевич интерпретировал как то, что предложения или пропозиции денотируют, но для которых, в отличие от Фреге, он ввел постоянные пропозициональные символы «1» и «0». Он задумал эту статью как первую часть монографии о трехзначной логике, которая, однако, так и не была завершена — вероятно, потому что Лукасевич был недоволен гибридным подходом, который уже устарел из-за его быстрого развития. Статья примечательна несколькими нововведениями. Используя символизм, заимствованный у Кутюра и Пирса, он вводит идею аксиоматического отрицания наряду с аксиоматическим утверждением, которое было, конечно, знакомо Фреге, Уайтхеду и Расселу. Константы «0» и «1» также встречаются в утверждаемых и отклоняемых формулах, фактически устанавливая объектно-языковую версию таблиц истинности. Чтобы показать это, мы используем более позднюю нотацию Лукасевича без скобок (см. приложение в конце статьи) и символы «⊢» для утверждения и «⊣» для отрицания, прочитываемые соответственно как «Я утверждаю» и «Я отрицаю». Первые принципы логики — это ⊢1 и ⊣0, но чтобы обозначить табуляцию для импликации, необходимо придерживаться следующих принципов: ⊢C00, ⊢C01, ⊣C10, ⊢C11. Когда Лукасевич использовал пропозициональные переменные, он квантифицировал их на манер Пирса, используя «Π» для квантора всеобщности и «Σ» для квантора существования.

Лукасевич и его ученики провели самостоятельное исследование пропозициональных исчислений: результаты, полученные между 1920 и 1930 годами, были опубликованы в совместной статье Лукасевича и Тарского 1930 года «Untersuchungen über den Aussagenkalkül». Работа велась как по классическим (бивалентным), так и по многозначным исчислениям. Наиболее яркая и полная демонстрация того, как Лукасевич в зрелом возрасте относился к классическому исчислению высказываний, содержится в его пособии для студентов 1929 года, основанном на конспектах лекций «Начала математической логики». Система вслед за Фреге основана только на импликации (C) и отрицании (N) с элегантным набором аксиом

CCpqCCqrCpr

CCNppp

CpCNpq

и тремя правилами вывода: modus ponens, правило равномерной подстановки формул для пропозициональных переменных и правило дефиниционной подстановки. На этой основе и используя чрезвычайно сжатую линейную нотацию для доказательств, противоположной крайности размашистых доказательств Фреге, Лукасевич доказывает около 140 теорем всего на 19 страницах.

Лукасевич, которому помогали и содействовали студенты и коллеги, не только Тарский, но и Адольф Линденбаум, Ежи Слупецкий, Болеслав Собочинский, Мордехай Вайсберг и другие, исследовал не только функционально полное пропозициональное исчисление с различными наборами связок в качестве базовых, включая функтор Шеффера D, но и частичные исчисления, а именно — чистое импликационное исчисление (основанное только на C) и чистое эквивалентное исчисление (основанное только на E). Они стремились найти наборы аксиом, удовлетворяющие ряду нормативных критериев: аксиом должно быть как можно меньше, они должны быть как можно более короткими, независимыми, с наименьшим количеством примитивов. Несомненно, в поиске все более совершенных систем аксиом был элемент соперничества, особенно в попытках подобрать единственную аксиому для различных систем, и это упражнение высмеивалось как чистый «спорт». Однако стремление улучшить системы аксиом было поиском логического совершенства, иллюстрацией того, что Ян Воленьский назвал «логикой ради логики». Одно время считалось, не без некоторого основания, что соревноваться могут только поляки. Когда Тарский однажды поздравил американского логика Эмиля Поста с тем, что он единственный неполяк, который внес фундаментальный вклад в логику высказываний, Пост ответил, что он родился в Августове, а его мать родом из Белостока. Позднее Лукасевич нашел в ирландском математике Кэрью Мередите достойного неполяка, который мог превзойти даже поляков в краткости своих аксиом.

Лукасевич использовал многозначные матрицы для установления независимости логических аксиом в системах Фреге, Рассела и других. Он доказал полноту общих, импликационных и эквивалентных исчислений и доказал, что эквивалентное исчисление может быть основано на единственной аксиоме EEpqErqEpr с заменой и отделением эквивалентности; показал далее, что никакая более короткая аксиома не может быть единственной аксиомой системы. Тарский показал в 1925 году, что чистое импликационное исчисление может быть основано на одной аксиоме, но ряд усовершенствований Вайсберга и Лукасевича привел к тому, что последний в 1936 году обнаружил, что формула CCCpqrCCrpCsp может служить одной аксиомой и что более короткой аксиомы будет недостаточно, хотя публикация этого результата должна была подождать до 1948 года.

Переменные пропозициональные функторы

Стандартное пропозициональное исчисление не использует ни кванторов, ни переменных функторов, то есть функторов одного или нескольких мест, принимающих пропозициональные аргументы, но которые, в отличие от таких постоянных функторов, как NN или CC, не имеют фиксированного значения. Такие переменные функторы действуют как предикаты логики предикатов первого порядка, за исключением принятия пропозициональных, а не номинальных аргументов. Таким образом, они усиливают выразительную силу логики. Лесьневский добавил как кванторы, так и связанные пропозициональные и функториальные переменные к пропозициональной логике и назвал полученную теорию прототетикой. Если оставить неписаными префиксные кванторы всеобщности, тезис прототетики состоит в том, что

CEpqCδpδq

где δ — одноместный пропозициональный функтор из той же синтаксической стабильности, что и отрицание или необходимость. Этот тезис является выражением закона экстенсиональности для пропозициональных выражений. Если p и q заменены сложными выражениями x и y, то тезис может быть использован для определения в импликативной форме Cδxδy.

Если δ заменяется первой частью сложного выражения, например, Cq или CCq0, то простое примыкание переменной, такой как p, для получения Cqp, CCq0p является непосредственным. Но если «пробел», в который должна войти переменная, не находится в конце, например Cpq, или если переменная должна быть вставлена более одного раза, как CCp0p, то простая процедура замены не будет работать. Лесьневский обошел проблему, введя вспомогательные определения, которые переносили требуемые прорезью переменные в нужное положение только с одним вхождением. Но Лукасевич счел эту процедуру неинтуитивной и расточительной. Его решение — которое фактически перекликается с практикой Фреге — состояло в том, чтобы позволить любому контексту, в котором одна пропозициональная переменная свободна, служить заменой для такого функтора, как δ, и отмечать места, в которых аргумент δ должен был быть прорезан, апострофом. Так что наши примеры выглядели бы так C’q, CC’0’. Эта более либеральная «замена апострофом» позволяет придать определениям удовлетворительно простую импликативную форму. Например, в пропозициональном исчислении, основанном на импликации и пропозициональной константе 0, отрицание может быть определено просто как CδNpδCp0. Использование переменных функторов с либеральной подстановкой позволяет дать поразительно сжатые и элегантные формулировки ряду принципов пропозициональной логики, например принципу бивалентности в виде

Cδ0CδC00δp

что может быть прочитано как «если что-то истинно для ложной пропозиции, то, если оно истинно и для истинной пропозиции, оно истинно для любой пропозиции» (где C00 ― истинная пропозиция). Высшие достижения сжатия с использованием переменных функторов были сделаны Мередитом, который показал, что вся классическая пропозициональная логика с переменными функторами может быть основана на одной аксиоме

CδpCδNpδq.

Еще более удивительно, что в 1951 году Мередит показал, что все бивалентное пропозициональное исчисление с кванторами и переменными функторами может быть выведено с помощью правил подстановки, отсоединения и кванторов из одной аксиоматической формулы

Cδδ0δp.

Лукасевич с восхищением описал это открытие как «шедевр дедуктивного искусства».

Интуиционистская логика

Лукасевич интересовался интуиционистской логикой не в последнюю очередь потому, что она, как и его собственная, отвергала закон исключенного третьего. В последней статье, опубликованной в 1952 году, он представил элегантную аксиоматизацию с десятью аксиомами, используя буквы F, T и O для интуиционистских связок импликации, конъюнкции и дизъюнкции соответственно, чтобы избежать столкновений, вызванных «конкуренцией» за эти связки. Интересно, что он сохранил обычное отрицание для обеих систем. Затем он показал, что можно определить классическую импликацию как NTpNq, сформулировал это определение с переменным функтором в качестве импликации

FδNTpNqδCpq

и доказал, что в этой версии классическая бивалентная логика, основанная на C и N, содержится в интуиционистской логике при условии, что отделение ограничивается только формулами C-N. Классические конъюнкция и дизъюнкция могут быть определены обычным способом как NCpNq и CNpq соответственно. Различая интуиционистские и классические связки, он меняет привычную точку зрения на то, что интуиционистское пропозициональное исчисление беднее теоремами, чем классическое: в формулировке Лукасевича все наоборот.

5. Многозначная логика

5.1 Возможность и третье значение

Самым известным достижением Лукасевича была разработка им многозначной логики. Эта революционная разработка произошла в контексте обсуждения модальности, в частности возможности. Современным логикам, привыкшим к тому, что модальная логика прививается к классической бивалентной логике, это может показаться странным. Но давайте рассмотрим, как Лукасевич пришел к этой идее. Если p — какое-либо предложение, пусть Lp означает «необходимо, что p», и Mp означает «возможно, что p». Два модальных оператора связаны обычной эквивалентностью ENLpMNp. Каждый принимает импликации CLpp и CpMp. Лукасевич предполагает, что каждый принимает также обратные импликации CpLp и CMpp, как это было бы с детерминистической точки зрения. Так получаем эквивалентности EpLp и EpMp, которые эффективно разрушают модальные различия. Добавим к этому идею, что возможность является двусторонней, то есть если что-то возможно, то возможно и его отрицание: EMpMNp. Из них сразу следует EpNp, и это парадоксально в двузначной логике. Выход, как описывает его Лукасевич, состоит в том, чтобы устранить модальные различия, не отвергая ни один из вышеприведенных принципов, а находя случай, когда EpNp истинен. Мы придерживаемся идеи, что высказывание Mp истинно, когда p не является ни истинным, ни ложным. В дополнение к истинностным значениям истина (1) и ложь (0) допустим тогда третье значение возможно, которое мы записываем как «½», так что, когда p не является ни истинным, ни ложным, это возможно, как и его отрицание Np, ведь если бы Np было истинно, p было бы ложным, и наоборот. Если Epq истинно, когда p и q имеют одинаковое значение истинности, то когда p возможно (мы пишем «|p|» для значения истинности p, поэтому |p|=½), мы имеем

|EpNp|=|E½½|=1

Именно так, с небольшими изменениями, Лукасевич вводит третье значение в своей первой опубликованной работе на эту тему, которая носит название «О понятии возможности». Эта короткая статья основана на дискуссии, состоявшейся 5 июня 1920 года во Львове. Через две недели на том же месте состоялась вторая дискуссия под более прозрачным названием «О трехзначной логике». В ней Лукасевич излагает принципы, регулирующие импликацию и эквивалентность, связанные с третьим значением. Они, в сущности, определяют таблицы истинности [2] для этих связок:

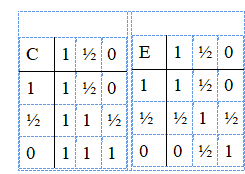
Вместе с принятыми определениями отрицания, конъюнкции и дизъюнкции как, соответственно,

Np=Cp0

Apq=CCpqq

Kpq=NANpNq

из этого получаются следующие таблицы истинности

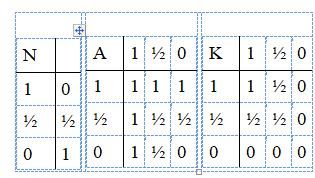
Лукасевич с гордостью заявляет, что «трехзначная логика имеет прежде всего теоретическое значение как первая попытка создать неаристотелевскую логику» (PL, 18; SW, 88). Ее практическое значение еще предстоит увидеть, а для этого нужно «сравнить с опытом следствия индетерминистского взгляда, который является метафизической основой новой логики».

Индетерминизм и третье значение

Последнее замечание раскрывает мотивацию Лукасевича заменить старую двузначную логику новой трехзначной — чтобы защитить индетерминизм и свободу. На самом деле эта идея осуществилась тремя годами раньше. Получив в 1918 году назначение на административную должность в Министерстве просвещения и собираясь на неопределенный срок оставить академическую жизнь, Лукасевич 17 марта выступил в Варшавском университете с «прощальной лекцией», в которой драматически заявил: «Я объявил духовную войну всякому принуждению, ограничивающему свободную творческую деятельность человека». Логической формой этого принуждения, по мнению Лукасевича, была аристотелевская логика, которая ограничивала предложения значениями истины и лжи. Его собственным оружием в этой войне была трехзначная логика. Вспоминая свою монографию 1910 года, Лукасевич отмечает следующее:

Поскольку Лукасевич был вовлечен в правление до конца 1919 года, только к 1920 году его открытия 1917 года стали доступны широкой академической общественности. Лукасевич вернулся к теме детерминизма для своей инаугурационной лекции в качестве ректора Варшавского университета 16 октября 1922 года. Эта лекция, прочитанная без заметок, но позднее записанная, дорабатывалась, хоть и несущественно, до 1946 года. Она была опубликована посмертно в 1961 году под названием «О детерминизме». Отличая логический детерминизм от каузального, Лукасевич утверждает, что если предсказание будущего случайного события, такого как действие, истинно в момент предсказания, событие должно произойти, поэтому единственный способ спасти свободу действий агента — это отрицать истинность предсказания и присвоить ему вместо этого третье истинностное значение — значение возможности.

Здесь не место вдаваться в проблемы с аргументацией Лукасевича. Достаточно сказать, что принцип EpLp необязательно должен быть принят детерминистами и что другие логики, рассматривавшие добавление третьего значения к логике, такие как (без ведома Лукасевича) Уильям Оккам, пришли к выводу, что нет никаких оснований отвергать бивалентность, отстаивая свободу, даже без учета компатибилистских взглядов.

Больше трех значений

Как только чары бивалентности были разрушены, естественным следующим шагом стало рассмотрение логики с более чем тремя значениями. В 1922 году Лукасевич рассказал, как делать таблицы истинности для стандартных связок в системах с конечным или бесконечным числом значений истинности в соответствии со следующими принципами, где значения истинности являются числами в интервале [0,1]:

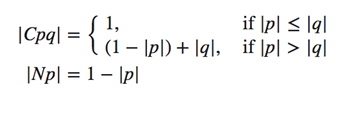
Предлагая логику с бесконечным числом значений, Лукасевич изобрел то, что гораздо позже (43 года спустя, если быть точным) было названо «нечеткой логикой». Комментируя эти системы в 1930 году, Лукасевич писал:

Мы обсудим эту философскую установку ниже.

Аксиомы и определения

С установлением табличного или матричного подхода к многозначным логикам, естественно было рассмотреть их аксиоматизацию. В этом помогали ученики Лукасевича. В 1931 году Вайсберг аксиоматизировал трехзначную систему Ł33 тезисами

CpCqp

CCpqCCqrCpr

CCNpNqCqp

CCCpNppp

Вайсберг также доказал гипотезу Лукасевича о том, что численно бесконечнозначная система Łℵ0ℵ0 может быть аксиоматизирована

CpCqp

CCpqCCqrCpr

CCCpqqCCqpp

CCCpqCqpCqp

CCNpNqCqp

Ни одна из этих систем не является функционально полной: существуют связки, не определимые только на основе C и N. Среди тех, которые поддаются определению, есть возможность M: еще в 1921 году Тарский показал, что она может быть определена как CNpp. В 1936 году Слупецкий показал, что, добавив функтор T, определяемый как |Tp|= ½ для всех значений p, все связки могут быть определены в Ł3. Для аксиоматизации этих функционально полных систем формулы

CTpNTp

CNTpTp

следует добавить к аксиомам Вайсберга.

Адольф Линденбаум показал, что Łn содержится в Łm (n<m) тогда и только тогда, когда n-1 является делителем m-1, поэтому, если ни один из них не делит другой, их соответствующие тавтологии должным образом пересекаются, но ни одно множество не содержится в другом. Тавтологии бесконечнозначной системы Łℵ0 содержатся в тавтологиях всех конечнозначных систем.

Дополнительно о модальности: система Ł

С 1917 года Лукасевич был доволен трехзначной логикой как формулировкой адекватных понятий модальности, предпочитая, как было отмечено, систему с бесконечным числом значений как наиболее точную. В какой-то момент, вероятно, около 1951–1952 гг., когда он работал над модальной логикой Аристотеля, Лукасевич изменил свое мнение. Существует целый ряд причин, лежащих в основе этого, но первой приходит на ум озабоченность Лукасевича тем, что в Ł3 существуют теоремы вида Lα, например LCpp. Почему это должно вызывать беспокойство, учитывая, что большинство «стандартных» модальных логик признают принцип, что если α является теоремой, то и Lα тоже? Лукасевич приводит два примера, чтобы оправдать беспокойство. Если =ab — это утверждение, что a тождественно b, то основывая тождество на двух аксиомах самотождественности и экстенсиональности

=aa

C=abCϕaϕb

то, подставляя затем L=a’ вместо ϕ, получаем

C=abCL=aaL=ab

и если мы принимаем L=aa, мы вынуждены заключить, что L=ab, что Лукасевич считает ложным (SW 392, AS 171), ссылаясь на пример Куайна (Quine 1953) (теперь устаревший, потому что число изменилось), что, хотя верно, что 9 = число планет, это не необходимая истина, хотя необходимо, что 9 = 9. Получаем

CMN=abN=ab

что значит, что если MN=ab, то N=ab. Но предположим, что a заменено на «число, выпавшее в результате этого броска кубика» и b ― на «число, выпавшее в результате следующего броска кубика». Антецедент может быть истинным, а консеквент ― ложным.

После многочисленных последующих обсуждений таких примеров Куайном, Крипке и другими эти примеры вряд ли убедительны, но есть еще одна более общая причина, по которой Лукасевич отвергает необходимость как теорему:

Поскольку LCpp была теоремой всех систем многозначной логики на тот момент, Лукасевичу нужно было придумать что-нибудь новое. Он сделал это в своей статье 1953 года «Системы модальной логики».

Лукасевич начинает работу с изложения условий, которым должна удовлетворять модальная логика. Они включают в себя аксиоматические отклонения, а также утверждения, такие как:

⊢CpMp

⊣CMpp

⊣Mp

⊢CLpp

⊣CpLp

⊣NLp

⊢EMpNLNp

⊢ELpNMNp

Чтобы получить систему модальной логики, учитывающую экстенсиональность для пропозициональных функторов, Лукасевич берет аксиому Мередита для пропозиционального исчисления C-N-δ

⊢CδpCδNpδq

и добавляет еще одно аксиоматическое утверждение и два аксиоматических отклонения

⊢CpMp

⊣CMpp

⊣Mp

вместе с правилами подстановки и отделения как для утверждения, так и для отвержения, чтобы получить свою логику. Принципы для утверждения обычные, в то время как принципы для отвержения следующие:

⊣Подстановка: Любая формула, имеющая отклоненный экземпляр подстановки, отклоняется.

⊣Отделение: Если Cab утверждается, а b отклоняется, то a отклоняется.

Из них он может вывести все желаемые принципы и экстенсиональность.

В этом и заключается логика Ł. В отличие от стандартной модальной логики, она имеет конечную характеристическую матрицу, где, как и Лукасевич, мы теперь заменяем «M» новым символом «Δ», где 1 ― обозначенное значение «истина», а 4 ― антиобозначенное значение «ложь».

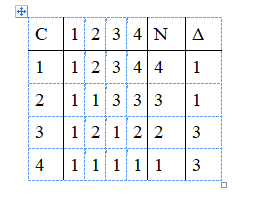
Матрица была доказана Смайли в 1961 году. Функторы необходимости (Γ) и конъюнкции определяются стандартным способом. Лукасевич отмечает, что существует еще один оператор возможности ∇ с таблицей истинности, также приведенной ниже:

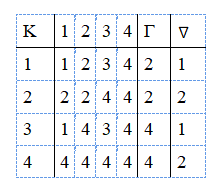
Взятую по отдельности, ее невозможно отличить от Δ, но два оператора вместе взаимодействуют иначе: в то время как ⊣ΔΔp и ⊣∇∇p, вместе они дают ⊢Δ∇p и ⊢∇Δp. Лукасевич сравнивает их с близнецами, которые неразличимы по отдельности, но различимы вместе. Похожие близнецы — оператор необходимости Γ и его копия (со значениями ¾), а также два промежуточных истинностных значения 2 и 3.

Эта логика очень отличается от более ранних мультивалентных систем Лукасевича и других модальных систем. Она отличается от его собственных систем тем, что является продолжением классической бивалентной логики и включает в себя все бивалентные тавтологии. Это меньше удивляет, если заметить, что четырехзначные матрицы для стандартных связок являются просто декартовым произведением стандартных бивалентных матриц с самими собой, а разница состоит в модальных операторах. Несколько особенностей отличают эту логику от стандартных модальных систем. Одна из них — полное отсутствие каких-либо истин, не говоря уже о теоремах вида Γa, в соответствии с отказом Лукасевича от истин «большего достоинства». Другие нечетные теоремы:

⊢CKΔpΔqΔKpq

все возможные высказывания являются совозможными

⊢CEpqCΔpΔq

материально эквивалентные высказывания возможны оба, если возможно одно

⊢CΔpCΔNpΔq

если пропозиция и ее отрицание возможны одновременно, то всё возможно.

Лукасевич знал о странных следствиях, но продолжал поддерживать свою систему. Несмотря на ряд попыток разобраться в системе, в целом был сделан вывод, что из-за этих странностей она на самом деле не является системой модальной логики. Если и есть одна главная тому причина, то это приверженность Лукасевича принципу экстенсиональности (функциональности истинности) даже для модальных операторов, из-за чего его учение о модальности стало мультивалентным в первую очередь.

История логики

Стоическая пропозициональная логика

Третьим большим достижением Лукасевича, наряду с его исследованиями многозначных и пропозициональных логик, является его работа по истории логики. Действительно, его можно с полным основанием считать отцом современного способа ведения истории логики, который принят, цитируя подзаголовок его книги о силлогистике Аристотеля, «с точки зрения современной формальной логики». Мы видели, что его ранняя книга о принципе противоречия у Аристотеля была относительно неудачной, хотя и продемонстрировала его способность проникать в самое сердце древнегреческих текстов.

Решающим событием в развитии Лукасевича как историка логики стало открытие им античной стоической логики. Он работал над диссертацией о стоиках и, чтобы подготовиться к ней, читал оригинальные тексты. Затем он обнаружил, что стоическая логика, вопреки тогдашнему общепринятому мнению, высказанному Прантлем, Целлером и другими, была не выхолощенной и ущербной аристотелевской силлогистикой, а ранней пропозициональной логикой, так что, например, первая недоказуемость стоиков «если первое, то второе; но не первое; следовательно, второе» ― это просто modus ponens или отделение для условия «если», а переменные, представленные не буквами, а порядковыми цифрами, являются пропозициональными переменными, а не переменными термов. Впервые он высказал эту точку зрения, которая сейчас, конечно, является стандартной, на встрече во Львове в 1923 году. Более систематическая трактовка 1934 года, «Об истории логики высказываний», представляет собой восхитительную виньетку с широким размахом: от стоиков, древних споров о значении кондиционалов, Петра Испанского и Оккама о законах Де Моргана и средневековой теории следствий до Фреге и современных пропозициональных исчислений. Современная оценка достижений стоической логики восходит к объяснению и его нескончаемой похвале стоиков, особенно Хрисиппа. Лукасевич понимал, что Прантль не знал постфрегеанскую логику и, несмотря на ошибочное отрицание Прантлем «глупости» многих стоических логик, по крайней мере предоставил полезные источники. Тем не менее Лукасевич язвительно отзывается о предшествующих историках логики:

Аристотель

В учебнике логики Лукасевича 1929 года после пропозиционального исчисления не излагается, как это было бы в наши дни, логика предикатов, а дается краткий формальный экскурс в категориальную (немодальную) силлогистику Аристотеля, предполагающую двенадцать теорем пропозиционального исчисления. Экскурс опережает книгу 1951 года Лукасевича «Силлогистика Аристотеля» на 22 года. Она произвела революцию в изучении логики Аристотеля и имела длинный и прерывистый генезис. Доклад на эту тему, прочитанный в Кракове в 1939 году, был опубликован на польском языке только в 1946 году. В 1939 году Лукасевич подготовил польскую монографию, но частичные корректуры и рукопись были уничтожены при бомбардировке Варшавы. В 1949 году он был приглашен читать лекции по силлогистике Аристотеля в Университетском колледже Дублина, и эти лекции легли в основу книги, завершенной в 1950 году и опубликованной в следующем году, его первой книги на английском языке. Первое издание касалось только категорической силлогистики. Для второго издания, завершенного в 1955 году, менее чем за год до его смерти, Лукасевич добавил три главы о модальной силлогистике, используя модальную логику, которую он разработал за это время. Второе издание было вычитано Леевским, который также составил для него указатели, и вышло в 1957 году.

Понимание Лукасевичем силлогистики Аристотеля основано на двух специфических интерпретационных принципах и общей позиции. Первый принцип состоит в том, что силлогизмы Аристотеля не являются, как традиционно предполагалось, схемами умозаключения вида «р, q, следовательно, r», но условными предложениями вида «если р и q, то r». Это непосредственно приводит ко второму принципу, который заключается в том, что за силлогистической трактовкой логики термов стоит более глубокая логика, логика пропозиций, и в частности логика оппозиций, «и» и «если», а также (в модальной силлогистике) «необходимо» и «возможно». Лукасевич считает, что этот пропозициональный базис иногда используется Аристотелем, например, при обработке косвенных доказательств, но по большей части негласно, и поэтому он считает законным критиковать Аристотеля (в отличие от стоиков) за то, что он явно не формулирует лежащую в основе пропозициональную логику. Резкие и противоречивые взгляды Лукасевича вызвали споры о том, как интерпретировать силлогистику. Хотя принципы и завоевали первых сторонников в Патциге (Patzig 1968), последующие критические замечания Коркорана (Corcoran 1972, 1974) и Смайли (Smiley 1974), сделанные независимо друг от друга, ясно установили, что силлогизмы — это не предложения, а умозаключения, и что Аристотель не нуждался в предварительной логике предложений. Эта точка зрения теперь преобладает среди исследователей логики Аристотеля. Оглядываясь назад, кажется, что Лукасевич стремился навязать Аристотелю свой собственный (фрегеанский) взгляд на логику как систему теорем, основанных на пропозициональной логике.

Другими словами, развитие современной логики, хотя и может высветить пробелы и недостатки логики Аристотеля, на самом деле выявляет ее достоинства, новшества и гениальность более четко, чем предыдущие традиционные или филологические исследования. Позиция Лукасевича преобладала и в настоящее время распространена среди тех, кто изучает логику Аристотеля, независимо от того, согласны они с его конкретными интерпретационными принципами или нет.

После изложения основ аристотелевской трактовки силлогистики, в которой он критикует более ранних комментаторов и отмечает, что Аристотель создал метод отклоненных форм, чтобы не только показать, какие из них являются валидными силлогизмами, но и доказать, что невалидные формы являются таковыми, Лукасевич представляет свою формализацию категорической силлогистики, основанную на следующих логических выражениях:

Рассматривая A и I как примитивы и определяя E=NI и O=NA, добавляем следующие аксиомы

вместе с modus ponens и правилом подстановки переменных термов. Именно такую систему предложил Лукасевич в своем учебнике 1929 года. Как указывает вторая аксиома, Лукасевич здесь следует Аристотелю. полагая, что все термы что-то обозначают. Можно добавить отклоненные формы: Лукасевич дает со второй фигуры

⊣CKAcbAabIac и

⊣CKEcbEabIAc

которые вместе с отделением и подстановкой обеспечивают все 232 отклоненных модуса Аристотеля. Вывод Лукасевича о категорической силлогистике Аристотеля состоит в том, что, несмотря на ее узость, это «система, точность которой превосходит даже точность математической теории, и в этом ее вечное достоинство» (AS, 131).

Модальная силлогистика, с другой стороны, мало изучена, по мнению Лукасевича, как потому, что она значительно ниже стандартов совершенства категорической силлогистики, так и из-за отсутствия «общепринятой системы модальной логики», которую, считает Лукасевич, обеспечил он вместе с системой Ł. Решение Лукасевича не является окончательным, хотя и дает материал для последующих исследований, и нам не следует останавливаться на нем здесь. Интересно, что в попытках Аристотеля в книге I, главе 15 «Первой аналитики» установить тезисы

CCpqCLpLq

CCpqCMpMq

Лукасевич видит одобрение идеи принципа экстенсиональности как для модальных операторов, так и для категорических.

Философская позиция

В ранней философии Лукасевича наиболее значимой и влиятельной позицией является его антипсихологизм в логике. На это оказали влияние Фреге, Гуссерль и Рассел. Терминологически это проявилось в замене Лукасевичем традиционного термина sąd (суждение), используемого Твардовским, термином zdanie (предложение). Это изменение точки зрения и терминологии было принято последующими польскими логиками в массовом порядке. После 1920 года Лукасевич был очень скуп в своих высказываниях относительно философии и философских проблем. Мы уже отмечали его неизменную приверженность индетерминизму. Основные его замечания и даже гнев были обращены в адрес тех, кто критикует место математической логики (или логистики, как ее тогда называли) в философии и мышлении вообще. Он отмечал определенные сходства в методе и стиле Львовско-Варшавской школы и Венского кружка, но критиковал последний за конвенционализм и отказ от всякой метафизики и за попытки превратить содержательные проблемы в языковые.

Именно его убежденность в том, что детерминизм ложен, заставляла его отвергать двухзначную логику. Сохраняя метафизическую нейтральность логики, он позже, в 1930-е годы, признал, что если раньше он был номиналистом, то теперь стал платоником. Источник этого убеждения изложен в конце его полемического текста 1937 года «В защиту логистики»:

Его платонистские установки нечасто выражались столь красноречиво.

В философии логики одно из самых глубоких убеждений Лукасевича, которое он разделял с другими логиками Варшавской школы, состояло в том, что логика должна быть экстенсиональной, что она является изучением исчислений не лингвистических значений или психологических суждений, а истинностных значений, будь то только классические два или более. Его точка зрения состоит в том, что предложения имеют истинностные значения и что логика — это наука о таких логических значениях, а не о предложениях (что является грамматикой), суждениях (что является психологией), о содержаниях, выражаемых пропозициями, или об объектах вообще (онтология). Он не доказывает эту позицию, а просто принимает и утверждает ее. Это имеет далеко идущие последствия для его трактовки модальной логики как многозначной.

В дополнение к общему отношению к научному философствованию, которое он заимствовал у Твардовского, есть один идентифицируемый источник некоторых других философских позиций Лукасевича относительно логики или, если не источник, то по крайней мере точка сходящихся убеждений. Один из них — это отказ от «сверхистины», стоящей выше обычной истины. Особенно отчетливо это проявляется в модальной логике. Другой — его симпатия к степеням возможности, промежуточным между истиной (1) и ложностью (0), в отличие от неколичественного третьего случая возможности (или в третьих случаях — близнецах Ł). Точно такое же различие между двумя видами возможности, «неувеличиваемой», без степеней, и «увеличиваемой», с бесконечными степенями, можно найти в массивном трактате Мейнонга 1915 года Über Möglichkeit und Wahrscheinlichkeit. Подобно Лукасевичу, Мейнонг не придает необходимым пропозициям более высокое достоинство, и, несмотря на наличие самой обширной онтологии, известной философии, в объектной теории Мейнонга отсутствуют необходимые объекты: он никогда не упоминает Бога, а идеальные объекты, такие как числа, для него имеют субсистенцию, но не экзистенцию, и причем не необходимую. Возможно, неслучайно, вернувшись во Львов после посещения Граца, Лукасевич в 1910 году говорил о законе исключенного третьего, заключая, что он, как и принцип противоречия, не является фундаментальным и имеет скорее практическое, чем логическое значение. Он предположил, что это не работает для общих объектов, таких как треугольник вообще, который не является ни равносторонним, ни неравносторонним. Мейнонг принимал такие объекты, которые он называл «неполными», и фактически перенял идею у учителя Лукасевича Твардовского. Лукасевич также рассматривал применение принципа к реальным объектам как «связанное с всеобщим детерминизмом явлений, не только настоящих и прошлых, но и будущих. Если бы кто-то отрицал, что все будущие явления сегодня уже предопределены во всех отношениях, он, вероятно, не смог бы принять рассматриваемый принцип». Трехзначная логика намечалась уже в 1910 году, после посещения Граца.

Мейнонг использовал множество значений возрастающей возможности, чтобы объяснить вероятность. Хотя процедура Лукасевича в его монографии 1913 года была основана на другой идее, ему по-прежнему казалось, что бесконечнозначная логика поможет понять вероятность. По крайней мере уже к 1935 году, с публикацией короткой статьи Тарского о вероятности и многозначной логике, он понял, что самый простой подход — отождествление вероятностей с истинностными значениями между 0 и 1 — не сработает. Причина в том, что из-за вероятностной зависимости вероятность не является экстенсиональной: если p — это пропозиция о том, что завтра в Дублине пойдет дождь, а Np — ее отрицание, вероятность противоречивой конъюнкции KpNp равна 0, но если p имеет степень истинности ½, то такую же степень истинности имеет и Np, и поэтому |KpNp|= ½ и в Ł3, и в Łℵ0. Несмотря на это, еще в 1955 году Лукасевич размышлял:

Наследие

Лукасевич однажды несколько нескромно заявил, что открытие многозначной логики сравнимо с открытием неевклидовой геометрии (SW 176). Каково бы ни было их значение, надежды Лукасевича на такую логику не оправдались. Семантика и чистая математика многозначных логик процветали, что привело к развитию MV-алгебр, используемых для алгебраической семантики логик Лукасевича. Бесконечнозначная или нечеткая логика имеет собственную математику, и выдающимся среди ее разработчиков является чешский математический логик Петр Хайек, работавший под влиянием Лукасевича. Нечеткая логика встречается во многих практических приложениях, где она используется для борьбы с неопределенностью, неточностью или отсутствием знания независимо от того, являются ли они одинаковыми или различными.

Его последняя логика Ł не поддается консенсусной интерпретации и рассматривается в лучшем случае как странная, а в худшем ― как тупиковая.

Выдающаяся работа, которую Лукасевич и его ученики проделали в логике и металогике пропозиционального исчисления, польской специализации на все более коротких аксиомах и так далее, теперь принадлежит ушедшему веку логистики. Его результаты действительно лишь изредка улучшались автоматическими проверками. С другой стороны, упор на логическую семантику, несмотря на обильное использование Лукасевичем истинностных значений, сместил акцент с аксиоматической виртуозности.

В истории логики новаторские исследования Лукасевича открыли новое и более плодотворное взаимодействие между прошлым и настоящим, и повторное открытие и новая оценка фигур из прошлого логики «в свете современной формальной логики» продолжается и по сей день, хотя не все собственные взгляды Лукасевича на то, как изучать к Аристотеля или стоиков, выдержали испытание временем. Его работа также вдохновила историков логики из католической традиции в Кракове, в первую очередь Яна Саламуху и Юзефа Бохеньского, которые применили современные методы к исследованию логических проблем и аргументов из истории философии.

В период расцвета Варшавской школы Лукасевич сыграл ключевую роль в воспитании следующего поколения логических исследователей и вдохновении их методами, результатами и проблемами. Даже идеи, которые он отбросил в качестве упражнений, изменили логику, например, предложение 1929 года формализовать неформальную процедуру доказательства из допущений привело к системе натурального вывода Станислава Ясковского 1934 года, по сути, именно по ней логика преподается сегодня студентам. Война безвозвратно прервала их работу. Некоторые из лучших учеников Лукасевича были евреями и были убиты в нацистских концлагерях. В изгнании из Польши после 1944 года Лукасевич не имел возможности продолжать эту педагогическую работу, занимая исследовательскую должность в непрофессиональном учебном заведении в стране без логической традиции. Его общение с современниками стало гораздо более редким, в основном он переписывался. Единственный известный логик, который взаимодействовал с Лукасевичем в это время и чьи труды пересекались с его интересами (время, модальность, многозначность) и отношениями (важность логики для философии) ― Артур Прайор, единственный крупный логик, принявший польскую нотацию, который потратил больше усилий, чем кто-либо, в попытке найти правдоподобную интерпретацию системы Ł. Справедливо также сказать, что из крупных фигур среди варшавских логиков Лукасевич получил наименьшее внимание со стороны комментаторов и историков. Монографий и статей о Лукасевиче относительно меньше, чем о других крупных деятелях Львовско-Варшавской школы.

Лукасевич справедливо гордился известностью, достигнутой польскими логиками в период между войнами, и вполне заслуживает того, чтобы его память была увековечена одной из четырех статуй Адама Мьяка, изображающих выдающихся членов Львовско–Варшавской школы у входа в Библиотеку Варшавского университета

Примечания автора к статье

1. Город Львов, родина Лукасевича и колыбель современной польской философии и логики, теперь находится в Украине (Львiв). Ранее будучи в cоставе Царства Польского, при первом разделе Речи Посполитой в 1772 году он был присоединен к Австрии и стал столицей Австрийского королевства Галиции и Лодомерии, просуществовавшего до 1918 года. Его немецкое название — Лемберг. Во время войны между Польшей и русским большевистским режимом его территория оспаривалась между двумя сторонами, а также теми, кто боролся за независимую Украину. В 1920–1939 гг. он был столицей Львовского воеводства во Второй Польской Республике. В 1939 году он был оккупирован Советским Союзом при разделе Польши, согласно заключенному с нацистской Германией по пакту Молотова — Риббентропа. После немецкого вторжения в Советский Союз в 1941 году он перешел под немецкий контроль, пока не был вновь захвачен Красной Армией в 1944 году. Несмотря на эти потрясения, город оставался в основном невредимым. Мирные договоренности 1945 года оставили город в составе Украинской ССР Советского Союза. После распада Советского Союза в 1991 году он стал главным городом Западной Украины. Человек, родившийся там в 1900 году и проживавший в городе до 2000 года, был бы подданным или гражданином нескольких разных государств — Австро-Венгрии, Польши, Советского Союза, Германии, Украины — и видел бы, как город десять раз переходил из рук в руки.

2. Эти таблицы следует читать следующим образом (где X — связка):

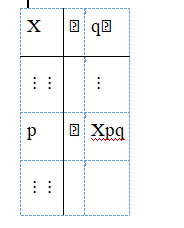
Приложение: Нотация Лукасевича без скобок, или польская нотация

Иногда говорят, что главным вкладом Лукасевича в логику было изобретение так называемой польской нотации. Ничто не может быть дальше от истины. Лукасевич действительно изобрел в 1924 году нотацию, которая известна как нотация Лукасевича или польская нотация, но это незначительная и очень случайная часть его талантливого творческого наследия, несравнимая с его научными достижениями в пропозициональной логике, многозначной логике и истории логики. Тем не менее мы используем обозначение в этой статье, и здесь будут уместны некоторые замечания.

В стандартной нотации Пеано — Рассела для пропозиционального исчисления символы бинарных связок (конъюнкция, дизъюнкция, импликация, эквивалентность и т.д.) записываются между их аргументами, например p∧q, p→q. Такая нотация известна как инфиксная, и она знакома нам по арифметическим операциям, таким как сложение и умножение. Для других формул, кроме простейших, она требует использования скобок для устранения неоднозначности: строка символов

[

p→q→r

]

Может иметь два смысла

p→(q→r)

и

(p→q)→r

которые имеют различные условия истинности: первое истинно, а второе ложно, когда все три аргумента ложны, например. Круглые скобки загромождают формулу визуально и графически. Пеано и Рассел вместо этого использовали кластеры точек для устранения неоднозначности формул, но, как и круглые скобки, их трудно понять визуально и отслеживать вручную, как только формулы становятся относительно сложными. Фреге в своей логической нотации ветвящегося дерева разработал элегантный способ записи пропозициональных формул без скобок, но он очень размашист и труден для набора, поскольку является нелинейным. Математики давно привыкли ставить символы общих функций перед своими аргументами, и Леон Чвистек упомянул об этом Лукасевичу в начале 1920-х годов как о возможности пропозициональных связей. Затем Лукасевич разработал принципы нотации, возможно, экспериментируя с деревянными блоками для составления формул. Все функторы (связки) записываются перед их аргументами, каждая связка представлена другой заглавной латинской буквой и имеет фиксированное число аргументов. На практике часто используются только унарные (одноместные) или бинарные (двуместные) связки. Пропозициональные переменные — это строчные латинские буквы. Корректность пропозициональных формул затем определяется рекурсивно:

1. Пропозициональная переменная, стоящая отдельно, является правильно построенной формулой.

2. Если Z — n-местная связка и a1,…,an — n правильно построенных формул, то Za1…an — правильно построенная формула

3. Ничто иное не является правильно построенной формулой.

Наиболее часто употребляемые в этой нотации связки с их инфиксными аналогами даны с их простейшими формулами:

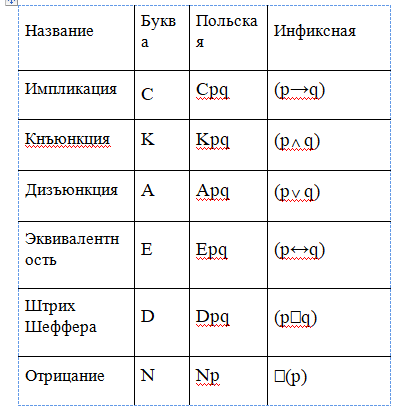
Формулы p→(q→r) и (p→q)→r соответствуют CpCqr и CCpqr, в то время как сложная формула, например

(((p→r)∧(q→r))∧((p→s)∧(q→s))↔((p∨q)→(r∧s)))

содержащая 43 символа, 20 из которых — скобки, выглядит po polsku как

EKKCprCqrKCpsCqsCApqKrs

с 23 символами, каждый из которых имеет значение.

Существует простой счетный тест на правильность формулировок пропозициональных формул в нотации Лукасевича. Начиная с начала (слева) формулы со счетом 1, добавьте 1 при каждом появлении бинарной связки, вычтите 1 при каждой пропозициональной переменной и оставьте счет одинаковым при каждой унарной связке. Формула правильно построена тогда и только тогда, когда счет впервые достигает нуля в конечной пропозициональной переменной. Помимо краткости и элегантности в эпоху между рукописным копированием и компьютеризированным набором нотация Лукасевича имела то преимущество, что ее можно было записать на обычной пишущей машинке без специальных символов.

Символизм требует небольших усилий, чтобы овладеть им, но, овладев им, с помощью такой нотации можно быстро понимать структуры формул. Это особенно эффективно для пропозиционального исчисления, в котором Лукасевич и его ученики преуспели. Для не-адептов она менее прозрачна. Юзеф Бохеньский рассказывал (в личном общении), что однажды, когда он перед войной ездил к Лукасевичу в Варшаву, Лукасевич взволнованно проводил его внутрь, указал на сложную формулу, начинающуюся чем-то вроде «ССС», и сказал: «Посмотрите на эту прекрасную и самоочевидно истинную формулу!» Истинность формулы не сразу стала очевидна ошеломленному Боченскому. Отсутствие обязательных скобок, однако, позволяет ориентирующемуся на читателя автору выделить группы букв необязательными скобками, чтобы более четко выявить структуру формулы. Это особенно эффективно практиковалось известным пользователем польской нотации Артуром Прайором.

Мы используем польскую нотацию в этой статье при обсуждении результатов Лукасевича в пропозициональном исчислении и силлогистике. Тем не менее, несмотря на свои внутренние достоинства и поддержку ряда логиков, прежде всего наиболее выдающихся, нотация Лукасевича не стала стандартной или даже широко распространенной. Она действительно гораздо менее полезна и эффективна, если ее распространить на исчисление предикатов, потому что объем квантора не диктуется другой структурой формулы. Она призвана разграничить область применения квантора с помощью скобок или других разделителей, а не к борьбе за сохранение свободы от скобок любой ценой. В математических калькуляторах и языках программирования симметрично связанная обратная польская нотация, где функторы следуют за аргументами, а не предшествуют им, была реализована в калькуляторах Hewlett-Packard и некоторых языках программирования. Несмотря на преимущества и наличие сторонников, эта нотация тоже пострадала, поскольку пользователи проголосовали за более традиционную инфиксную нотацию, требующую круглых скобок.

Библиография

Общие замечания

Названия даются на языке оригинала, а в случае произведений, первоначально написанных на польском языке, за ними следует название любого опубликованного английского перевода, если он существует, или наш собственный английский перевод, если его нет. Библиография опубликованных работ Лукасевича не является полной, так как большое количество его опубликованных работ состоит из резюме на одну или две страницы или тезисов докладов, прочитанных в различных местах, какой была практика в Польше того времени. Такие тексты были включены лишь в том случае, если важны для развития идей Лукасевича или изложения его взглядов. Переводы на другие языки, кроме английского и русского, не были включены, за исключением монографии 1910 года об Аристотеле.

Обширная библиография на польском языке, составленная редактором Яцеком Юлиушем Ядацким, опубликована в сборнике Logika i Metafizyka (1998), в котором переиздана большая часть эссе Лукасевича, а также ряд примечательных речей, рецензий и выдержек из переписки, дана биографическая хронология и опубликовано большое количество фотографий.

Сокращения

● (AS) Aristotle's Syllogistic from the Standpoint of Modern Formal Logic, 2nd ed.

● (PF) Przegląd Filozoficzny

● (PL) Polish Logic, 1920–1939, ed. S. McCall.

● (PWN) Państwowe Wydawnictwo Naukowe

● (RF) Ruch Filozoficzny

● (SW) Selected Works, ed. L. Borkowski.

● (Z) Z zagadnień logiki i filozofii. Pisma wybrane, ed. J. Słupecki.

Источники

Сборники

● Z zagadnień logiki i filozofii. Pisma wybrane. [Topics in Logic and Philosophy. Selected Writings], ed. J. Słupecki. Warsaw: PWN, 1961.

● Selected Works, ed. L. Borkowski. Amsterdam: North-Holland, 1970.

● Logika i Metafizyka. Miscellanea. [Logic and Metaphysics. A Miscellany], ed. J. J. Jadacki. Warsaw: Towarzystwo Naukowe Warszawskie, 1998.

● Pamiętnik. [Diary], ed. J. J. Jadacki and P. Surma. Warsaw: Wydawnictwo Naukowe Semper, 2013. [Contains diary entries by Łukasiewicz and a number of incidental pieces of biographical note by him and others.]

Монографии (русские переводы)

● Аристотелевская силлогистика с точки зрения современной формальной логики. М.: Издательство иностранной литературы, 1959.

● О принципе противоречия у Аристотеля. Критическое исследование. М.: Центр гуманитарных инициатив, 2012.

Монографии (на других языках)

● Die logischen Grundlagen der Wahrscheinlichkeitsrechnung. Kraków: Spółka Wydawnicza Polska, 1913. Translation: Logical Foundations of Probability Theory, in SW, 16–63.

● Elementy logiki matematycznej. Skrypt autoryzowany, ed. M. Presburger. Warsaw: Wydawnictwo Koła Matematyczno-Fizycznego Słuchaczów Uniwersytetu Warszawskiego, 1929. 2nd ed., ed. J. Słupecki, Warsaw: PWN, 1958. Translation: Elements of Mathematical Logic. Oxford: Pergamon Press, 1966.

Статьи

● O indukcji jako inwersji dedukcji [On induction as the inversion of deduction]. PF 6 (1903), 9–24, 138–152.

● Analiza i konstrukcja pojęcia przyczyna [Analysis and construction of the concept of cause]. PF 9 (1906), 105–179.

● O zasadzie wyłączonego środka. PF 13 (1910), 372–3. Translation: On the Principle of the Excluded Middle. History and Philosophy of Logic 8 (1987), 67–9.

● Über den Satz von Widerspruch bei Aristoteles. Bulletin internationale de l’Académie des Sciences de Cracovie, Classe de Philosophie (1910), 15–38. Translation: On the Principle of Contradiction in Aristotle. Review of Metaphysics 24 (1970/71), 485–509; Aristotle on the Law of Contradiction, in: J. Barnes, M. Schofield and R. Sorabji, eds., Articles on Aristotle 3. Metaphysics. London: Duckworth, 1979, 50–62.

● O twórczości w nauce, Księga pamiątkowa ku uczczeniu 250-tej rocznicy zalożenia Uniwersytetu Lwowskiego przez Króla Jana Kazimierza r. 1661. Lwów: Uniwersytet Lwowski, 1912, 3–15. Translation: Creative elements in science, in SW, 1–15.

● W sprawie odwracalności stosunku racji i następstwa [Concerning the reversibility of the relation between reason and consequence], PF 26 (1913), 298–314.

● O nauce i filozofii [On science and philosophy], PF 28 (1915), 190–196.

● O pojęciu wielkości, PF 19 (1916), 1–70. Translation: On the concept of magnitude. in SW, 64–83.

● Treść wykładu pożegnalnego wygłoszonego w auli Uniwersytetu Warszawskiego 7 marca 1918 r. Pro arte et studio 3 (1918), 3–4. Translation: Farewell lecture delivered in the Warsaw University Lecture Hall on March 7, 1918, in SW, 84–6.

● O pojęciu możliwości, RF 5 (1920), 169–170. Translation: On the concept of possibility, in PL, 15–16.

● O logice trójwartościowej, RF 5 (1920), 170–1. Translation: On three-valued logic, in PL, 16–18, and in SW, 87–8.

● Logika dwuwartościowa, PF 23 (1921), 189–205. Translation: Two-valued logic, in SW, 89–109.

● Interpretacja liczbowa teorii zdań, RF 7 (1922/23), 92–3. Translation: A numerical interpretation of the theory of propositions, in SW, 129–30.

● O logice stoikow [On Stoic logic], PF 30 (1927), 278–9.

● O znaczeniu i potrzebach logiki matematycznej [On the importance and needs of mathematical logic], Nauka Polska 10 (1929), 604–20.

● (with A. Tarski) Untersuchungen über den Aussagenkalkül, Comptes rendus de la Société des Sciences et des Lettres de Varsovie, cl. iii, 23 (1930), 1–21. Translation: Investigations into the Sentential Calculus, in SW, 131–52.

● Philosophische Bemerkungen zu mehrwertigen Systemen des Aussagenkalküls, Comptes rendus de la Société des Sciences et des Lettres de Varsovie, cl. iii, 23 (1930), 51–77. Translation: Philosophical remarks on many-valued systems of propositional logic, in PL, 40–65, and in SW, 153–78.

● Uwagi o aksjomacie Nicoda i “dedukcji uogólniającej”, Księga pamiątkowa Polskiego Towarzystwa Filozoficznego, Lwów, 1931, 366–83. Translation: Comments on Nicod's axiom and on “generalizing deduction”, in SW, 179–96.

● Ein Vollstandigkeitsbeweis des zweiwertigen Aussagenkalküls, Comptes rendus de la Société des Sciences et des Lettres de Varsovie, cl. iii, 24 (1931), 153–83.

● Z historii logiki zdań, PF 37 (1934), 417–37. Translation: On the history of the logic of propositions, in PL, 66–87, and in SW, 197–217.

● Znaczenie analizy logicznej dla poznania [The importance of logical analysis for cognition], PF 37 (1934), 369–77.

● Bedeutung der logischen Analyse für die Erkenntnis, Actes du VIII Congrès International de Philosophie, Prague (1936), 75–84.

● W obronie logistyki. Myśl katolicka wobec logiki wspólczesnej, Studia Gnesnensia 15 (1937), 12–26. Translation: In defence of logistic, in SW, 236–49.

● Kartezjusz [Descartes], Kwartalnik Filozoficzny 15 (1938), 123–8.

● Geneza logiki trójwartościowej [The origins of three-valued logic]. Nauka Polska 24 (1939). 215–223.

● O sylogistyce Arystotelesa [On Aristotle's syllogistic], Sprawozdania PAU, 44 (1939), 220–7. Published 1946.

● Der Äquivalenzkalkül, Collectanea logica 1 (1939), 145–69. Did not appear then. One offprint survived in Münster, and served for the translation: The Equivalential Calculus, in PL, 88–115, and in SW, 250–77.

● Die Logik und das Grundlagenproblem, Les entretiens de Zurich sur les fondements et la méthode des sciences mathématiques 6–9.XII.1938, Zurich: Leemann, 1941, 82–100.

● The shortest axiom of the implicational calculus of propositions, Proceedings of the Royal Irish Academy, Sect. A, 52 (1948), 25–33.

● W sprawie aksjomatyki implikacyjnego rachunku zdań [On the system of axioms of the implicational prepositional calculus], Annales de la Société Polonaise de Mathématique 22 (1950), 87–92.

● On Variable Functors of Propositional Arguments, Proceedings of the Royal Irish Academy, Sect. A, 54 (1951), 25–35.

● On the intuitionistic theory of deduction, Indagationes Mathematicae. Koninklijke Nederlandse Academie van Wetenschappen, Proceedings Series A 14(1952), 201–212, repr. in SW, 325–40.

● Sur la formalisation des théories mathématiques. Colloques internationaux du Centre National de la Recherche Scientifique, 36: Les méthodes formelles en axiomatique, Paris, 1953, 11-19. Translation: Formalization of Mathematical Theories, in SW, 341–51.

● A System of Modal Logic, The Journal of Computing Systems, 1 (1953), 111–49, repr. in SW, 352–90.

● Arithmetic and Modal Logic, The Journal of Computing Systems, 1 (1954), 213–9, repr. in SW, 391–400.

● The principle of individuation, Proceedings of the Aristotelian Society, supplementary volume XXVII (Berkeley and modern problems) (1953), 69–82.

● On a controversial problem of Aristotle's modal syllogistic, Dominican Studies 7 (1954), 114–28.

● Curriculum vitae [1953], Philosophical Studies 6 (1956), 43–6.

● O determinizmie, in Z, 114–26. Translation: On determinism, in PL 19–39, and in SW, 110–28.

Переводы

● David Hume, Badania dotycące rozumu ludzkiego [Исследование о человеческом разумении]; trans. Jan L. Łukasiewicz and Kazimierz Twardowski. Lwów: Nakładem Polskiego Towarzystwa Filozoficznego, 1905.

Литература

● Зиновьев, А.А. Философские проблемы многозначной логики. М.: Издательство Академии Наук СССР, 1960.

● Agassi, A. and Woleński, J., 2010, Łukasiewicz and Popper on Induction. History and Philosophy of Logic, 31: 385–388. [Contains English translation of two small texts of Łukasiewicz on induction.]

● Betti, A., 2002, The incomplete story of Łukasiewicz and bivalence. In: T. Childers, ed., The Logica 2002 Yearbook, Prague: The Czech Academy of Sciences—Filosofia, 21–36.

● Childers, T. and Majer, O., 1998, On Łukasiewicz's theory of probability, in K. Kijania-Placek and J. Woleński, eds., The Lvov-Warsaw School and Contemporary Philosophy, Dordrecht: Kluwer, 303–12.

● Corcoran, J., 1972, Completeness of an Ancient Logic, Journal of Symbolic Logic, 37: 696–705.

● –––, 1974, Aristotelian Syllogisms: Valid Arguments or True Universalized Conditionals?, Mind, 83: 278–81.

● Font, J. P. and Hájek, P., 2002, On Łukasiewicz's Four-Valued Modal Logic. Studia Logica, 70: 157–82.

● McCall, S. (ed.), 1967, Polish Logic 1920–1939, Oxford: Clarendon Press.

● Malinowski, G., 1993, Many-Valued Logics, Oxford: Clarendon Press.

● Patzig, G., 1968. Die aristotelische Syllogistik, Göttingen: Vandenhoeck and Ruprecht, 3rd ed. (1st ed. 1959.) Translation: Aristotle's Theory of the Syllogism, tr. J. Barnes, Dordrecht: Reidel, 1969.

● Prior, A. N., 1954, The Interpretation of Two Systems of Modal Logic. The Journal of Computing Systems, 1: 201–8.

● Quine, W. V., 1953, Three Grades of Modal Involvement. Proceedings of the XIth International Congress of Philosophy (Vol. XIV), Brussels, pp. 80 ff.

● Schmidt am Busch, H.-C. and Wehmeier, K. F., 2007, On the relations between Heinrich Scholz and Jan Łukasiewicz. History and Philosophy of Logic, 28: 67–81.

● Seddon, F., 1996, Aristotle and Łukasiewicz on the Principle of Contradiction. Ames: Modern Logic Publishing.

● Simons, P., 1992, Łukasiewicz, Meinong, and Many-Valued Logic. In K. Szaniawski, ed., The Vienna Circle and the Lvov-Warsaw School. Dordrecht: Kluwer, 1989, 249–91, repr. in P. Simons, Philosophy and Logic in Central Europe from Bolzano to Tarski. Dordrecht: Kluwer, 193–225.

● Smiley, T. J., 1961, On Łukasiewicz's Ł-modal system. Notre Dame Journal of Formal Logic, 2: 149–53.

● –––, 1974, What is a Syllogism?, Journal of Philosophical Logic, 2: 136–154.

● Sobociński, B., 1956, In memoriam Jan Łukasiewicz (1878–1956). Philosophical Studies, 6: 3–49. [Includes as an appendix Łukasiewicz's Curriculum Vitae of 1953.]

● Tarski, A., 1935/6, Wahrscheinlichkeitslehre und mehrwertige Logik. Erkenntnis, 5: 174–5.

● Wójcicki, R. and Malinowski, G. (eds.), 1977, Selected Papers on Łukasiewicz's Sentential Calculi. Wrocław: Ossolineum.

● Woleński, J., 1994, Jan Łukasiewicz on the Liar Paradox, Logical Consequence, Truth, and Induction. Modern Logic, 4: 392–400.

● –––, 2000, Jan Łukasiewicz und der Satz vom Widerspruch, in: N. Öffenberger and M. Skarica, eds. Beiträge zum Satz vom Widerspruch und zur Aristotelischen Prädikationtheorie. Hildesheim: Olms, 1–42.

● –––, 2013, The Rise of Many-Valued Logic in Poland, in his Historico-Philosophical Essays, Vol. 1. Kraków: Copernicus Press, 37–50.