математика

Поделиться статьей в социальных сетях:

в избранное

Теория множеств

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 8 октября 2014; содержательно переработано 12 февраля 2019

Теория множеств — это математическая теория о вполне определенных совокупностях, называемых множествами, содержащиеся в них объекты называются членами или элементами множества. Чистая теория множеств работает исключительно со множествами, то есть она рассматривает только те множества, элементы которых также представляют собой множества. Теория наследственно конечных множеств — чьи элементы также являются конечными множествами, которые также состоят из конечных элементов и т.д. — формально эквивалентна арифметике. Таким образом, суть теории множеств состоит в изучении бесконечных множеств, следовательно, ее можно определить как математическую теорию об актуально бесконечном (в противовес потенциально бесконечному).

Понятие множества настолько простое, что обычно его определяют неформальным образом и считают чем-то само собой разумеющимся. Однако в теории множеств, как это часто происходит в математике, множества задаются аксиоматически, поэтому их существование и базовые свойства постулируются при помощи соответствующих формальных аксиом. Аксиомы теории множеств предполагают существование настолько богатого теоретико-множественного универсума, что все математические объекты можно представить в виде множеств. Кроме того, формальный язык чистой теории множеств позволяет формализовать все математические понятия и аргументы. Таким образом, теория множеств становится стандартным основанием математики, поскольку всякий математический объект можно рассматривать в виде множества и всякую математическую теорему можно логически вывести в исчислении предикатов из аксиом теории множеств.

Оба аспекта теории множеств, а именно, теория множеств как математическое исследование бесконечности и как основание математики, обладают философской значимостью.

Истоки

Теория множеств как отдельная математическая дисциплина берет свое начало в работах Георга Кантора. Можно сказать, что теория множеств появилась на свет в 1873 году, когда он совершил потрясающее открытие, установив, что линейный континуум, то есть вещественная прямая, несчетен — иными словами, что входящие в прямую точки нельзя посчитать с помощью натуральных чисел. Так, даже если и множество натуральных чисел, и множество действительных чисел являются бесконечными, действительных чисел больше, чем натуральных — и осознание этого факта послужило толчком для возникновения идеи множеств с различными объемами бесконечности (см. обсуждение истоков идей теории множества и их использования различными математиками и философами до Кантора и в его время в статье о ранних этапах развития теории множеств).

Согласно Кантору, два множества A и В обладают одинаковым объемом, или кардинальностью, если элементы множества А можно поставить во взаимно-однозначное соответствие элементам множества В. Таким образом, множество N натуральных чисел и множество R действительных чисел характеризуются различной кардинальностью. В 1878 году Кантор сформулировал знаменитую континуум-гипотезу (CH), в которой утверждается, что всякое конечное множество действительных чисел является одинаково счетным — то есть характеризуется той же кардинальностью, что и N, либо той же кардинальностью, что R. Иными словами, существуют только два возможных объема бесконечных множеств действительных чисел. CH представляет наиболее известную проблему теории множеств. Сам Кантор приложил немало усилий для ее развития — как и многие другие крупнейшие математики первой половины XX века, в частности Гильберт — расположивший CH в начало своего знаменитого списка из 23 неразрешенных проблем математики, представленных в 1900 году во время Второго Международного Конгресса Математиков в Париже.

Вплоть до сегодняшнего дня проблема СН остается открытой.

Уже на раннем этапе понятия так называемой наивной теории множеств порождали всякие противоречия и парадоксы; в частности, парадоксы возникают из, казалось бы, естественного допущения о том, что всякое свойство задает множество, а именно — множество объектов, обладающих данным свойством. Известным примером служит так называемый парадокс Рассела, также известный Цермело:

Таким образом, некоторые совокупности, подобно совокупности всех множеств, совокупности всех ординальных чисел или совокупности всех кардинальных чисел, не являются множествами. Такие совокупности называются собственными классами.

Для того, чтобы избежать парадоксов и найти твердое основание для теории множеств, необходимо задать для нее систему аксиом. Первую попытку аксиоматизации теории множеств предпринял Цермело (Zermelo 1908); к этому его подтолкнула необходимость установления базовых теоретико-множественных принципов, на которые опиралось бы его доказательство канторовского принципа вполне упорядоченного множества. Аксиоматизация Цермело позволяет избежать парадокса Рассела с помощью аксиомы выделения, которая формулируется как количественная оценка свойств множеств — то есть она представляет собой высказывание второго порядка.

Дальнейшая работа, проведенная Скулемом и Френкелем, привела к формализации аксиомы выделения с помощью формул первого порядка, заменивших неформальное понятие свойства, а также к введению аксиомы преобразования, которая также была сформулирована в виде схемы аксиом для формул первого порядка (см. следующий раздел). Аксиома преобразования необходима для правильного развития теории трансфинитных ординальных и кардинальных чисел с использованием трансфинитной рекурсии (см. раздел 3).

Было также необходимо доказать существование такого простого множества, как множество наследственно конечных множеств, т.е. таких конечных множеств, которые состоят из конечного числа элементов, элементы которых также конечны и т.д.; или доказать базовые теоретико-множественные утверждения, например то, что всякое множество содержится в транзитивном множестве — то есть множестве, содержащем все элементы, входящие в состав элементов данного множества (о погрешностях теории множеств Цермело см. Mathias 2001). Дальнейшее появление аксиомы регулярности, предложенное фон Нейманом, привело к установлению стандартной аксиоматической системы теории множеств, известной как аксиомы Цермело — Френкеля с добавлением аксиомы выбора, или ZFC.

Прочие аксиоматизации теории множеств (например, аксиоматизация фон Неймана —Бернайса — Гёделя или Морза — Келли) также позволяют нам проводить формальный анализ собственных классов.

Аксиомы теории множеств

Аксиомы Цермело — Френкеля с добавлением аксиомы выбора (ZFC) — это системы аксиом, сформулированных в первопорядковой логике с равенством и единственным символом бинарного отношения ∈, обозначающим принадлежность. Так, запись A∈B означает, что А является элементом множества В. Ниже мы приводим неформализованную запись аксиом ZFC.

Аксиомы ZFC

● Аксиома объемности: Если элементы двух множеств А и В совпадают, то эти множества равны.

● Аксиома пустого множества: Существует множество, обозначаемое как ∅ и называемое пустым множеством, в которое не входят никакие элементы.

● Аксиома пары: Для любых множеств А и В существует множество, обозначаемое {A,B}, которое содержит А и В в качестве своих единственных элементов. Также существует множество {А}, которое содержит А в качестве единственного элемента.

● Аксиома множества подмножеств (аксиома булеана): Для любого множества А существует множество, обозначаемое Р(А) и называемое множеством подмножеств А, элементами которого являются все подмножества А.

● Аксиома объединения: Для любого множества А существует множество, обозначаемое ⋃A, которое называется объединением А, и элементами которого являются все элементы, входящие в состав хотя бы одного из множеств элементов А.

● Аксиома бесконечности: Существует некоторое бесконечное множество. Существует множество Z, которое содержит ∅, так что если A∈Z, то ⋃{A,{A}}∈Z.

● Аксиома выделения: для всякого множества А и всякого заданного свойства существует множество, содержащее все элементы А, обладающие данным свойством. Свойство задается формулой φ первопорядкового языка теории множеств.

Таким образом, аксиома выделения — это не одна аксиома, а схема аксиом, то есть бесконечный список аксиом — по одной для каждой формулы φ.

● Аксиома преобразования: Для всякой определенной функции, область определения которой задает множество А, существует множество, элементами которого являются все значения данной функции. Аксиома преобразования также представляет собой схему аксиом, поскольку определенные функции задаются формулами.

● Аксиома регулярности: Всякое непустое множество А содержит минимальное подмножество, то есть такое подмножество, которому не принадлежит никакой другой элемент множества А.

Так выглядят аксиомы теории множеств Цермело — Френкеля (ZF). Аксиомы пустого множества или пары выводятся из других аксиом ZF, так что их можно опустить. Кроме того, из аксиомы преобразования выводится аксиома выделения.

Наконец, существует аксиома выбора (АС):

● Аксиома выбора: Для всякого множества А попарно непересекающихся непустых множеств существует множество, содержащее ровно один элемент из каждого подмножества А.

Долгое время АС считалась противоречивой аксиомой. С одной стороны, она очень полезна и широко используется в математике. С другой стороны, ее следствия контринтуитивны; таковым является например, парадокс Банаха — Тарского, который гласит, что один шар можно разделить на конечное множество частей, из которых затем можно собрать два шара. Возражения против данной аксиомы произрастают из того факта, что в ней утверждается существование множеств, которые невозможно эксплицитно определить. Однако приведенное Гёделем в 1938 году доказательство ее непротиворечивости — относительно непротиворечивости ZF — позволило отбросить все сомнения, остававшиеся в связи с этой аксиомой.

Аксиома выбора эквивалентна (по модулю ZF) принципу вполне упорядоченного множества, который гласит, что всякое множество можно представить как вполне упорядоченное — то есть линейно упорядочить его таким образом, что всякое непустое подмножество этого множества содержало минимальный элемент.

Хотя формально это и не является необходимым, помимо символа ∈, как правило, для обозначения принадлежности используются другие специальные символы. Например, выражение А⊆B означает, что А является подмножеством В, то есть всякий член А является членом В. Прочие символы используются для обозначения множеств, полученных при применении базовых операций, например, A∪B обозначает объединение множеств А и В — множество, элементами которого являются элементы А и В; или A∩B обозначает пересечение А и В — множество, элементы которого являются общими для А и В. Упорядоченная пара (А,В) определяется как множество {{А},{А,В}}. Таким образом, две упорядоченные пары (А,В) и (С,D) равны, если и только если А=С и В=D. Декартово произведение (или прямое произведение)) A×B определяется как множество упорядоченных пар (С,D), таких что C∈A и D∈B. Для любой формулы φ(x,y1,…,yn) и множеств A,B1,…,Bn можно сформировать множество всех элементов А, которые удовлетворяют формуле φ(x,B1,…,Bn). Это множество обозначается так: {a∈A:φ(a,B1,…,Bn)}. В ZF можно легко доказать, что все эти множества существуют.

Теория трансфинитных ординальных и кардинальных чисел

В ZFC можно развить канторову теорию трансфинитных (то есть бесконечных) ординальных и кардинальных чисел. Согласно определению, данному фон Нейманом в начале 1920-х годов, ординальные числа, или ординалы, мы получаем, производя две операции над элементами множества, начиная с пустого множества: берем следующий за ним элемент и переходим к предельному. Так, первым ординальным числом является ∅. Если существует ординал α, то непосредственно следующий за ним элемент, обозначаемый α+1, составляет множество α∪{α}. И если мы возьмем непустое множество Х ординалов, таких что для всякого α∈X следующий за ним α+1 также входит в Х, то мы получим предельный ординал ⋃X. Всякий ординал (строго говоря) вполне упорядочен за счет ∈, т.е. он линейно упорядочен за счет ∈ и не существует бесконечной ∈-нисходящей последовательности. Кроме того, любое вполне упорядоченное множество изоморфно единственному ординалу, называемому его порядковым типом.

Отметим, что всякий ординал равен множеству предшествующих ему элементов. Однако класс ON всех ординалов не составляет множество. Иными словами, ON был бы ординалом, превосходящим все ординалы, а это невозможно. Первый бесконечный ординал, который является множеством всех конечных ординалов, обозначается греческой буквой омега (ω). В ZFC конечные ординалы отождествляются с натуральными числами. Тогда ∅=0, {∅}=1, {∅,{∅}}=2 и т.д., следовательно, ω является просто множеством N натуральных чисел.

Список этих операций можно расширить, прибавив к нему умножение натуральных чисел на все ординалы. Например, ординал α+β является порядковым типом вполне упорядоченного множества, полученного за счет объединения вполне упорядоченного множества порядкового типа α и вполне упорядоченного множества порядкового типа β. Начало последовательности ординалов, вполне упорядоченных с помощью операции ∈, выглядит так:

0, 1, 2, …, n, …, ω, ω+1, ω+2, …, ω+ω, …, n⋅ω, …, ω⋅ω, …, ωn, …, ωω, …

Ординалы удовлетворяют принципу трансфинитной индукции: предположим, что С является классом ординалов таким, что, если С содержит все ординалы β, меньшие, чем некоторый ординал α, то α также содержится в С. Тогда класс С будет содержать все ординалы. Используя трансфинитную индукцию, можно доказать важнейший принцип трансфинитной рекурсии в ZFC (для этого понадобится схема преобразования), который гласит, что для произвольной функции класса G:V→V можно определить функцию класса F:ON→V такую, что F(α) является значением функции G, примененным к функции F, ограниченной до α. Можно использовать трансфинитную рекурсию, например, для того, чтобы определить свойство арифметических операций сложения, умножения и возведения в степень на ординалах.

Не будем забывать, что бесконечное множество счетно, если его можно поставить во взаимно-однозначное соответствие с ω. Все приведенные выше ординалы являются либо конечными, либо счетными. Но множество всех конечных и счетных ординалов также является ординалом, называемым ω1, и он не является счетным. Аналогичным образом, множество всех ординалов, которые можно привести во взаимно-однозначное соответствие некоторому ординалу, меньшему или равному ω1, также является ординалом, называемым ω2, причем его нельзя привести во взаимно-однозначное соответствие с ω1, и т.д.

Кардинальные числа

Кардинальное число — это ординал, который нельзя привести во взаимно-однозначное соответствие меньшему ординалу. Таким образом, всякий конечный ординал является кардинальным числом, и ω, ω1, ω2 и т.д. также являются кардинальными числами. Бесконечные кардинальные числа обозначаются буквой алеф (ﭏ) ивритского алфавита, и их последовательность индексируется ординалами: ℵ0, ℵ1, ℵ2, …, ℵω, ℵω+1, …, ℵω+ω, …, ℵω2, …, ℵωω, …, ℵω1, …, ℵω2, …

Таким образом, ω=ℵ0, ω1=ℵ1, ω2=ℵ2 и т.д. Для всякого кардинального числа существует превосходящее его кардинальное число, и пределом возрастающей последовательности кардинальных чисел также является кардинальное число. Таким образом, класс всех кардинальных чисел не составляет множество, но является собственным классом.

Бесконечное кардинальное число κ также называется регулярным, если оно не является объединением меньшего, чем κ числа меньших кардинальных чисел. Тогда ℵ0 является регулярным, и таковыми же являются все бесконечные последующие кардиналы, например ℵ1. Нерегулярные бесконечные кардинальные числа называют сингулярными. Первым сингулярным кардинальным числом является ℵω, так как оно представляет собой объединение счетной последовательности меньших кардинальных чисел — т.е. ℵω=⋃n<ωℵn.

Конфинальностью кардинального числа κ, обозначаемого как cf(κ), является наименьшее кардинальное число λ такое, что κ является объединением λ меньших ординалов. Тогда cf(ℵω)=ℵ0.

Согласно аксиоме выбора (в виде принципа вполне упорядоченных множеств), всякое множество А может быть вполне упорядоченным, так как его элементы можно привести во взаимно-однозначное соответствие с единственным кардинальным числом, называемым кардинальностью А. Для кардинальных чисел κ и λ сумма κ+λ будет определяться как кардинальность множества, состоящего из объединения любых двух равномощных множеств (между которыми можно установить взаимно-однозначное соответствие), при этом кардинальностью одного множества будет κ, а другого — λ. Произведение κ⋅λ определяется как кардинальность декартова произведения κ×λ. Операции сложения и умножения бесконечных кардинальных чисел тривиальны, ибо если κ и λ — бесконечные кардинальные числа, тогда κ+λ=κ⋅λ=maximum{κ,λ}.

Напротив, возведение в степень кардинальных чисел — крайней нетривиальная операция, ибо даже значение простейших нетривиальных бесконечных степеней — 2ℵ0 — неизвестно и не может быть определено в ZFC (см. ниже). Кардинальное число κλ определяется как кардинальность декартова λ-кратного произведения κ; таким же образом определяется кардинальность множество всех функций от λ до κ. Согласно теореме Кёнига, κcf(κ)>κ, а это значит, что конфинальность кардинального числа 2ℵ0, каким бы оно ни было, должна быть несчетной. В сущности, это все, что можно сказать о значении степени 2ℵ0 исходя из ZFC.

В случае возведения в степень сингулярных кардинальных чисел ZFC позволяет нам сказать гораздо больше. В 1989 году Сахарону Шелаху удалось прийти к важному выводу, что если ℵω является строгим пределом, т.е. 2ℵn<ℵω для любого n<ω, тогда 2ℵω<ℵω4 (см. Shelah 1994). Технику доказательства этой теоремы и аналогичных ей теорем в ZFC, разработанную Шелахом, называют теорией pfc (possible confinalities — теория возможных конфинальностей). Эта теория нашла множество применений и в других разделах математики.

Универсум всех множеств V

Апостериори аксиомы ZF — помимо аксиомы объемности, не требующей обоснования, поскольку в ней просто утверждается некоторое свойство множеств — можно обосновать через их использование в построении кумулятивной иерархии множеств. То есть в ZFC мы определяем использование трансфинитных рекурсий функций класса, предписывающих каждому ординалу α множество Vα, заданное следующим образом:

● V0=∅

● Vα+1=P(Vα)

● Vα=⋃β<αVβ, всегда, когда α — предельный ординал.

Аксиома булеана используется для того, чтобы получить Vα+1 из Vα. Схемы преобразования и объединения позволяют построить Vα для α предельного ординала. Действительно, представим функцию, предписывающую каждому β<α множество Vβ. По схеме преобразования, совокупность всех Vβ для β<α является множеством, следовательно, аксиома объединения, примененная к этому множеству, дает Vα. Аксиома бесконечности необходима для доказательства существования ω, а следовательно — и трансфинитной последовательности ординалов. Наконец, аксиома регулярности, исходя из остальных аксиом, равнозначна утверждению, что всякое множество принадлежит некоторому универсуму Vα с некоторым ординалом α. Таким образом, ZF доказывает, что теоретико-множественный универсум, называемый V, представляет собой объединение всех Vα, если α — ординал.

Собственный класс V вкупе с отношением ∈ удовлетворяет всем аксиомам ZFC, а следовательно — и модели ZFC. Он является предполагаемой моделью ZFC; можно сказать, что ZFC задает описание V. Впрочем, как мы увидим далее, это описание весьма неполное.

Одним из важных свойств V является так называемый принцип рефлексивности. То есть для всякой формулы φ(x1,…,xn) ZFC доказывает, что существует некоторый универсум Vα, который ее отражает, иными словами, что для всякого a1, …, an∈Vα, φ(a1,…,an) выполняется в V, если и только если φ(a1,…,an) выполняется в Vα.

Таким образом, V нельзя охарактеризовать никаким высказыванием, поскольку всякое высказывание, которое является истинным в V, также должно быть истинным в некотором исходном сегменте Vα. В частности, ZFC нельзя аксиоматизировать окончательно, в противном случае ZFC доказывала бы, что для неограниченного набора ординалов α Vα является моделью ZFC — а это противоречит второй теореме Гёделя о неполноте (см. раздел 2).

Принцип рефлексивности воплощает сущность теории множеств ZF, ведь, как показал Леви (Levy 1960), аксиомы объемности, выделения и регулярности вкупе с принципом рефлексивности, сформулированным в качестве схемы аксиом, утверждающей, что всякую формулу отображает некоторое множество, содержащее все элементы и все подмножества его элементов (отметим, что Vα таковым является), — всё это равнозначно ZF.

Теория множеств как основание математики

Всякий математический объект можно рассматривать как множество. Например, натуральные числа отождествляются с конечными ординалами: N=ω. Множество целых чисел Z можно определить как множество эквивалентных классов пар натуральных чисел, выполняющих условие (n,m)≡(n′,m′) если и только если n+m′=m+n′. Отождествляя всякое натуральное число n с эквивалентным классом пар (n,0), можно легко перенести правила сложения и произведения натуральных чисел на Z (подробнее см. в Enderton 1977; альтернативное построение см. в Levy 1979). Далее можно определить рациональные числа Q как множества эквивалентных классов пар (n,m) целых чисел, где m≠0 при выполнении равенства (n,m)≡(n′,m′), если и только если n⋅m′=m⋅n′. Опять же, операции сложения и произведения на Z можно естественным образом перенести на Q. Кроме того, упорядочение ≤Q на дроби задается следующим образом: r≤Qs, если и только если существует t∈Q такое, что s=r+t Действительные числа можно определить как дедекиндовы сечения Q: действительное число задается парой (А,В) непустых равномощных множеств, так что A∪B=Q и a≤Qb для всех a∈A и b∈B. Тогда мы можем, опять же, перенести операции сложения и умножения на Q, а также упорядочение ≤Q на множество действительных чисел R.

Подчеркнем, что здесь не утверждается, что, скажем, действительные числа являются дедекиндовыми сечениями рациональных чисел, ведь их также можно представить с помощью последовательности Коши или как-то иначе. Что важно с точки зрения обоснования, так это то, что теоретико-множественная версия R вкупе с обычными алгебраическими операциями удовлетворяет основополагающим аксиомам, которым удовлетворяют действительные числа, а именно аксиомам полного упорядоченного поля. Метафизический вопрос о том, чем на самом деле являются действительные числа, здесь роли не играет.

Алгебраические структуры можно также рассматривать как множества, раз всякое n-арное отношение элементов множества А можно представить как множества из n элементов (a1, …, an) элементов А. И всякую n-арную функцию f на А, область значения которой составляет множество В, можно представить в виде множества из n+1 элементов ((a1, …, an),b) такое, что b является значением f на (a1, …, am). Таким образом, например, группа представляет собой простую тройку (А,+,0), где А — непустое множество, + является бинарной функцией на А (т.е. ассоциативной), 0 — элемент А такой, что а+0=0+а=а для всех а∈А, и для всех а∈А существует элемент А, обозначаемый –а, такой что a+(−a)=(−a)+a=0. Кроме того, топологическое пространство представляет собой просто множество Х вкупе с топологией τ на этом множестве, то есть τ является подмножеством Р(Х), содержащим Х и ∅, замкнутым относительно произвольных объединений и конечных пересечений.

Всякое математическое утверждение можно формализовать при помощи языка теории множеств, и всякую математическую теорему можно вывести из аксиом ZFC или некоторых следствий из ZFC, используя исчисление логики первого порядка. Именно в этом смысле теория множеств служит основанием математики.

Хотя роль обоснования математики является безусловно значимой для теории множеств, тем не менее это далеко не единственная причина, по которой ее стоит изучать. Идеи и техники, разработанные в рамках теории множеств, например, комбинаторика, метод вынуждения или теория больших кардиналов — все это превратило ее в глубокую и захватывающую математическую теорию, которая достойна изучения сама по себе и может находить важные применения практически во всех разделах математики.

Метаматематика

Благодаря тому примечательному факту, что практически всю математику можно формализовать в ZFC, возможно исследование самой математики при помощи математических средств. Так, любой вопрос, связанный с существованием математического объекта или доказуемостью допущения или гипотезы, можно представить в строгой математической формулировке. Благодаря этому и возможна метаматематика — математическое исследование самой математики. Таким образом, вопрос о доказуемости или недоказуемости любого математического утверждения становится осмысленной математической проблемой. Сталкиваясь с открытой математической проблемой или гипотезой, имеет смысл задаться вопросом о ее доказуемости или недоказуемости в рамках формальной системы ZFC. К сожалению, ответ может отсылать к чему-то третьему, поскольку даже если ZFC действительно непротиворечива, все же она неполна.

Феномен неполноты

Из теоремы Гёделя о неполноте для логики первого порядка следует, что ZFC непротиворечива — то есть что из нее нельзя вывести противоречие — если и только если у нее есть модель. Моделью ZFC является пара (М,Е), где М — непустое множество, а Е — бинарное отношение на М, такое что все аксиомы ZFC будут истинны, если интерпретировать их в (М,Е), то есть если фигурирующие в аксиомах переменные пробегают элементы М и ∈ интерпретируется как Е. Таким образом, если φ — выражение языка теории множеств и можно найти модель ZFC, в которой φ истинно, то его отрицание, ¬φ, невозможно доказать в ZFC. Следовательно, если мы можем найти модель φ, а также модель ¬φ, то невозможно доказать ни истинность, ни ложность φ в рамках ZFC, и в таком случае мы должны сказать, что φ неразрешимо или независимо от ZFC.

В 1931 году Гёдель заявил о своих поразительных теоремах о неполноте, в которых утверждалось, что любые формальные системы для математики непременно должны быть неполными. В частности, если ZFC непротиворечива, то в ZFC должны существовать неразрешимые утверждения. Кроме того, вторая теорема Гёделя о неполноте предполагает, что формальное (арифметическое) выражение CON(ZFC), утверждающее, что даже если ZFC действительно непротиворечива, утверждение о ее непротиворечивости невозможно доказать в самой ZFC. И также невозможно доказать обратное. Таким образом, CON(ZFC) неразрешима в ZFC.

Если ZFC непротиворечива, тогда в ней нельзя доказать существование модели ZFC, ведь в противном случае ZFC доказывала бы свою непротиворечивость. Таким образом, доказательство непротиворечивости или неразрешимости данного высказывания φ всегда будет лишь относительно непротиворечивым. То есть мы заключаем, что ZFC непротиворечива, поскольку у нее есть модель, и затем мы строим другую модель ZFC, в которой φ истинно. В последующих разделах мы рассмотрим несколько примеров.

 Теория множеств континуума

Со времен Кантора и примерно до 1940 года теория множеств в основном развивалась в связи с проблемой континуума, то есть действительной линии R. Главным предметом исследования были так называемые свойства регулярности, а также другие структурные свойства легко определяемых множеств действительных чисел — этот раздел математики известен под названием дескриптивной теории множеств.

 Дескриптивная теория множеств

Дескриптивная теория множеств — это исследование свойств и структур определенных множеств действительных чисел и, в более общем виде, определенных подмножеств Rn и прочих польских пространств (топологических пространств, которые гомеоморфны отдельным полным метрическим пространствам), например, бэровского пространства N всех функций f:N→N, пространства комплексных чисел, гильбертова пространства и отдельных банаховых пространств. Простейшие множества действительных чисел являются базовыми открытыми множествами (открытыми интервалами с конечными точками, заданными рациональными числами) и их дополнениями. Множества, которые можно получить в результате конечного числа шагов, начиная с базовых открытых множеств, применяя операции дополнения и составления счетного объединения ранее полученных множеств — это борелевские множества. Все борелевские множества являются регулярными, то есть они пользуются всеми классическими свойствами регулярности. Одним из примеров регулярного свойства является измеримость Лебега: ко множеству действительных чисел применима мера Лебега, если оно отлично от борелевского множества за счет пустого множества, то есть множества, которое можно покрыть множествами с базовыми открытыми интервалами сколь угодно малой длины. Таким образом, проще говоря, ко всякому борелевскому множеству применима мера Лебега, однако более сложные множества, чем борелевское, могут быть неизмеримы. Другими классическими свойствами регулярности являются бэровское свойство (множество, состоящее из действительных чисел, обладает бэровским свойством, если оно отличается от открытого множества за счет остаточного множества, а именно множества, представляющего собой счетное объединение множеств, которые не являются плотными ни на одном интервале), а также свойство совершенного множества (множество, состоящее из действительных чисел, обладает свойством совершенного множества, либо если оно счетно, либо если оно содержит совершенное множество, то есть непустое замкнутое множество без изолированных точек). В ZFC можно доказать существование нерегулярных множеств, состоящих из действительных чисел, однако для этого необходима АС (Solovay 1970).

Аналитические множества, также называемые Σ11, являются непрерывными образами борелевских множеств; а коаналитические множества (или Π11) являются дополнениями аналитических множеств.

Исходя из аналитических (или коаналитических) множеств и применяя операцию проекции (из произведения пространства R×N на R) и дополнения, мы получим проективные множества. Проективные множества образуют иерархию возрастающей сложности. Например, если A⊆R×N является коаналитическим, тогда проекция {x∈R:∃y∈N((x,y)∈A)} является проективным множеством уровня сложности, следующего за коаналитическими множествами. Такие множества называются Σ12, а их дополнения называются Π12.

Проективные множества довольно часто встречаются в математической практике, ведь множество А, состоящее из действительных чисел, является проективным, если и только если его можно определить в структуре

R=(R,+,⋅,Z).

То есть существует формула первого порядка φ(x,y1,…,yn) в языке для такой структуры, что для некоторого r1,…,rn∈R будет верно A={x∈R:R⊨φ(x,r1,…,rn)}.

ZFC доказывает, что всякое аналитическое множество, а следовательно, и всякое коаналитическое множество поддаются мере Лебега и обладают бэровским свойством. Она также доказывает, что всякое аналитическое множество обладает свойством совершенного множества. Однако свойство совершенного множества для коаналитических множеств предполагает, что первое несчетное кардинальное число ℵ1 является большим кардинальным числом в построенном универсуме L (см. раздел 7) —так называемым недостижимым кардинальным числом (см. раздел 10), которое предполагает, что в ZFC невозможно доказать, что любое коаналитическое множество обладает свойством совершенного множества.

Теория проективных множеств более высокой сложности, чем коаналитические, полностью не определена ZFC. Например, в L существует множество Σ12, которое является неизмеримым и не обладает бэровским свойством, в то время как, если аксиома Мартина верна (см. раздел 11), всякое такое множество обладает такими свойствами регулярности. Но все же есть аксиома, называемая аксиомой проективной детерминированности (PD), которая совместима с ZFC, что означает непротиворечивость некоторых больших кардинальных чисел (по сути, это следует из самого существования некоторых больших кардинальных чисел), и которая предполагает, что все проективные множества являются регулярными. Кроме того, PD позволяет разрешить большинство вопросов, связанных с проективными множествами. Подробнее см. статью о больших кардинальных числах и детерминированности.

 Детерминированность

Свойство регулярности множеств, включающее все прочие классические свойства регулярности, — это свойство детерминированности. Для простоты мы будем работать с бэровским пространством N. Мы помним, что элементами N являются функции f:N→N, то есть последовательности натуральных чисел с длиной ω. Пространство N топологически эквивалентно (то есть гомеоморфно) множеству иррациональных точек R. Таким образом, поскольку нас интересуют свойства регулярности подмножеств R и поскольку счетными множествами, такими как множество рациональных чисел, можно пренебречь в плане этих свойств, мы также можем работать с N вместо R.

При данном A⊆N пусть будет игра, связанная с А; обозначим ее как GA. В ней участвуют двое игроков, Игрок 1 и Игрок 2, которые по очереди делают ход ni∈N: Игрок 1 делает ход n0, затем Игрок 2 делает ход n1, затем Игрок 1 делает ход n2 и т.д. Так, на шаге 2k Игрок 1 совершает ход n2k, а на шаге 2k+1 Игрок 2 ходит n2k+1. Можно наглядно представить последовательность этой игры следующим образом:

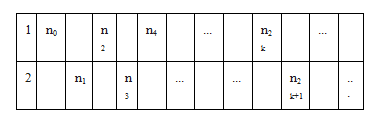
После бесконечного числа шагов два игрока производят бесконечную последовательность натуральных чисел. Игрок 1 выигрывает игру, если последовательность принадлежит А. В противном случае побеждает Игрок 2.

Игра GA является детерминированной, если существует победная стратегия для одного из игроков. Победная стратегия для одного из игроков, скажем, для Игрока 2 — это отображение σ из множества конечных последовательностей натуральных чисел в N такое, что, если игрок действует согласно этой функции, то есть играет σ(n0,…,n2k) на ходу k, он всегда будет побеждать в игре, что бы при этом ни делал другой игрок.

Мы будем говорить, что подмножество А множества N является детерминированным, если и только если игра GA является детерминированной.

В ZFC (при этом необходимо применение АС) можно доказать, что существуют недетерминированные множества. Таким образом, аксиома детерминированности (AD), которая гласит, что все подмножества N являются детерминированными, несовместима с АС. Однако Дональду Мартину удалось доказать в рамках ZFC, что всякое борелевское множество является детерминированным. Кроме того, он показал, что если существует большое кардинальное число, называемое измеримым (см. раздел 10), то даже аналитические множества являются детерминированными. Аксиома проективной детерминированности (PD) утверждает, что всякое проективное множество является детерминированным. Выходит, что, согласно PD, все проективные множества действительных чисел являются регулярными. Вудин показал, что в некотором смысле PD позволяет разрешить практически все проблемы, связанные с проективными множествами. Более того, по-видимому, PD для этого просто необходима. Другая аксиома, ADL(R), утверждает, что AD истинна в L(R) — в наименьшем транзитивном классе, содержащем все ординалы и все действительные числа, и удовлетворяющем аксиомам ZF (см. раздел 7). Таким образом, ADL(R) подразумевает, что любое множество, состоящее из действительных чисел, которое принадлежит L(R), является регулярным. Кроме того, так как ADL(R) содержит все проективные множества, то из ADL(R) следует PD.

Континуум-гипотеза

В континуум-гипотезе (СН). сформулированной Кантором в 1878 году, говорится о том, что кардинальность всякого бесконечного множества, состоящего из действительных чисел, будет либо ℵ0, либо она будет равна кардинальности всего множества R. Таким образом, СН равнозначна 2ℵ0=ℵ1.

Кантор доказал в 1883 году, что замкнутые множества действительных чисел обладают свойством совершенного множества, из чего следует, что всякое несчетное замкнутое множество, состоящее из действительных чисел, характеризуется той же кардинальностью, что R. Таким образом, СН истинна для замкнутых множеств. Более 30 лет назад Павел Александров расширил этот результат до всех борелевских множеств, а затем Михаил Суслин доказал, что СН истинна для всех аналитических множеств. Следовательно, все аналитические множества удовлетворяют СН. Однако попытки доказать, что все коаналитические множества удовлетворяют СН, не увенчаются успехом, поскольку это невозможно доказать в рамках ZFC.

В 1938 году Гёдель доказал непротиворечивость СН и ZFC. Исходя из предположительной непротиворечивости ZFC, он выстраивает модель ZFC, известную как конструктивный универсум, в котором СН истинна. Так, доказательство показывает, что если ZF непротиворечива, то непротиворечивы ZF и АС, а также ZF и СН. Следовательно, если мы допускаем непротиворечивость ZF, то АС невозможно будет опровергнуть в ZF — и СН также будет невозможно опровергнуть в ZF.

Обзор текущих дискуссий вокруг данной проблемы, включая недавние результаты, полученные Вудином, см. в статье, посвященной континуум-гипотезе.

Конструктивный универсум Гёделя

Конструктивный универсум Гёделя, обозначаемый как L, задается с помощью трансфинитной рекурсии на ординалах, подобно V, но на последующих ступенях вместо того, чтобы получить множество Vα+1 из множества Vα, нам требуются только те подмножества Lα, которые можно определить в Lα, если использовать элементы Lα в качестве параметров. Таким образом, если PDef(X) обозначает множество всех подмножеств Х, определимых в структуре (Х,∈) за счет формул языка теории множеств, используя элементы Х в качестве параметров определения, мы получаем

● L0=∅

● Lα+1=PDef(Lα)

● Lλ=⋃α<λLα, если λ — предельный ординал.

Тогда L — совокупность всех Lα, где α — ординал, то есть L=Uα∈ONLα.

Гёдель показал, что L удовлетворяет всем аксиомам, а также удовлетворяет СН. Действительно, он удовлетворяет обобщенной континуум-гипотезе (GCH), то есть 2ℵα=ℵα+1 для всякого ординала α.

Высказывание V=L, называемое аксиомой конструктивности, утверждает, что всякое множество принадлежит L. Это утверждение истинно в L, так как оно не противоречит ZFC, и из него следует как AC, так и GCH.

Собственный класс L вкупе с отношением ∈, ограниченным до L, является внутренней моделью ZFC, то есть он является транзитивным (содержащим все элементы, входящие в его элементы) классом, который содержит все ординалы и удовлетворяет всем аксиомам ZFC. По сути, это наименьшая внутренняя модель ZFC, поскольку она содержится в любой другой внутренней модели.

В более общем виде, располагая произвольным множеством А, мы можем построить наименьшую транзитивную модель ZF, содержащую А и все ординалы, так же как и L, но теперь начиная с транзитивного замыкания {A}, наименьшего транзитивного множества, содержащего А, вместо ∅. Полученная в результате модель L(A), однако, необязательно должна быть моделью АС. Одной очень важной такой моделью является L(R) — наименьшая транзитивная модель ZF, содержащая все ординалы и все действительные числа.

Развитие теории конструктивных множеств многим обязано трудам Рональда Дженсена. Он развил так называемую теорию тонкой структуры L и выделил некоторые комбинаторные принципы — такие как ♢ и □, — которые можно использовать для того, чтобы вывести сложные конструкции неисчислимых математических объектов. Теория тонкой структуры также играет очень важную роль в анализе больших L-образных моделей, таких как L(R) или внутренних моделей для больших кардиналов (см. раздел 10.1).

Вынуждение

В 1963 году, спустя двадцать пять лет после гёделевского доказательства непротиворечивости СН и АС относительно ZF, Пол Коэн (1969) доказал непротиворечивость отрицания СН, а также отрицания АС относительно непротиворечивости ZF. Таким образом, если ZF непротиворечива, тогда СН неразрешима в ZFC, а АС неразрешима в ZF. Чтобы достичь этого результата, Коген применил новую и чрезвычайно действенную технику, называемую вынуждением или форсингом (forcing), для расширения счетных транзитивных моделей ZF.

Так как из аксиомы V=L следует АС и СН, то любая модель отрицания АС или СН должна противоречить V=L. Давайте же проиллюстрируем идею вынуждения в случае построения модели для отрицания V=L. Мы начнем с транзитивной модели М для ZFC, которая, как мы можем допустить, не теряя степени обобщенности, является моделью V=L. Чтобы прийти в противоречие с V=L, нам нужно расширить М за счет прибавления нового множества r таким образом, чтобы в рамках расширенной модели r было неконструктивным множеством. Так как все наследственно конечные множества являются конструктивными, мы должны прибавить бесконечное множество натуральных чисел.

Первая проблема, с которой мы сталкиваемся, состоит в том, что М может уже содержать все подмножества ω. К счастью, по теореме Лёвенгейма — Скулема для первопорядковой логики, М характеризуется элементарной подмоделью N. Таким образом, поскольку нас интересуют только утверждения, истинное в М, а не М как таковая, мы также можем допустить, что сама М является счетной. Тогда, коль скоро P(ω) несчетно, то существует огромное число подмножеств ω, не принадлежащих М. Однако, к сожалению, мы не можем просто взять любое бесконечное множество r или ω, не принадлежащее М, и добавить его в М, поскольку r может содержать много информации, так что, если добавить его в М, М перестанет быть моделью ZFC или же будет оставаться моделью V=L. Чтобы этого избежать, нам нужно тщательно подобрать r. Идея состоит в том, чтобы r было родовым для М, то есть чтобы r выстраивалось из конечных аппроксимаций таким образом, чтобы оно не обладало никаким свойством, которое было бы определимым в М и которое можно избежать. Например, если мы рассматриваем r как бесконечную последовательность натуральных чисел, расположенную в возрастающем порядке, свойство r, содержащего только конечный ряд четных чисел, можно избежать, потому что при любой конечной аппроксимации r — то есть при всяком конечном увеличении последовательности натуральных чисел — мы всегда можем расширить это множество, добавив еще четных чисел, так что в конце конструирования r будет содержать бесконечно много четных чисел; хотя и нельзя будет избежать свойства содержания числа 7, ведь когда конечная аппроксимация к r содержит число 7, тогда оно будет присутствовать, каким бы образом мы ни проводили построение r. Так как М счетно, то такие родовые r существуют. Тогда расширенная модель M[r], которая включает М и содержит новое множество r, будет называться родовым расширением М. Коль скоро мы допускаем, что М — транзитивная модель V=L, то модель M[r] является просто Lα(r), где α — супремум ординалов М. Тогда при помощи принудительного отношения между конечными аппроксимациями к r и формулами в языке теории множеств, расширенной за счет так называемых имен для множеств в родовых расширениях, мы можем показать, что М[r] является моделью ZFC и что r невозможно построить в M[r], а следовательно, аксиома конструктивности V=L будет опровержена.

В общем и целом, вынужденное расширение модели М достигается за счет прибавления к М родового подмножества G некоторого частично упорядоченного множества Р, принадлежащего М. В приведенном выше примере Р было бы множеством всех конечных возрастающих последовательностей натуральных чисел, рассматриваемых как конечных аппроксимации к бесконечным последовательностям r, упорядоченным при помощи ⊆; а G было бы множеством всех конечных исходных сегментов r.

В случае непротиворечивого доказательства отрицания СН мы начинаем с модели М и прибавляем ℵ2 новых подмножеств ω, так что в родовом расширении СН опровергается. В таком случае нам необходимо использовать соответствующее частичное упорядочение Р, так чтобы ℵ2, содержащееся в М, не схлопнулось, то есть чтобы оно совпадало с ℵ2 родового расширения, и таким образом родовое расширение М[G] будет удовлетворять утверждению, согласно которому существует ℵ2 действительных чисел.

Другие применения метода вынуждения

Помимо СН, техника вынуждения используется во многих других математических задачах и проблемах, связанных с континуумом и прочими бесконечными математическими объектами, которые оказались неразрешимыми в ZFC.

Один из наиболее важных примеров представляет гипотеза Суслина (SH). Кантор доказал, что всякое линейно упорядоченное множество S без крайних точек, которое является плотным (между любыми двумя различными элементами S можно указать еще один элемент), полным (у всякого ограниченного сверху подмножества S есть супремум) и обладает плотным счетным подмножеством, будет изоморфно вещественной прямой. Суслин предположил, что это также будет верно, если смягчить требование о содержании плотного счетного множества, сказав, что всякая совокупность попарно-равномощных интервалов является счетной. В начале 1970-х годов Томас Жеч придумал последовательный контрпример с использованием техники вынуждения, а Рональд Дженсен доказал, что данный контрпример существует в L. Примерно в это же время Роберт Соловей и Стэнли Тенненбаум (Solovey and Tennenbaum 1971) разработали и впервые применили итерированную технику вынуждения, чтобы построить модель, в которой бы выполнялась SH, тем самым показывая ее независимость от ZFC. Чтобы убедиться в том, что SH выполняется в родовом расширении, необходимо опровергнуть все контрпримеры, однако опровергнув один конкретный контрпример, мы можем случайно произвести другие, так что нам придется использовать технику вынуждения вновь и вновь; в сущности, нам пришлось бы продолжать эту операцию по меньшей мере на протяжении ω2 шагов. Именно поэтому нам необходима итерация вынуждения.

Среди прочих известных математических проблем, неразрешимость которых в ZFC удалось доказать, благодаря технике вынуждения, в частности за счет применения итерированного вынуждения, иногда в сочетании с большими кардинальными числами, можно назвать проблему измерения и гипотезу Бореля в связи с мерой множества, гипотезу Капланского об алгебре Банаха, а также проблему теории групп Уайтхеда.

Поиск новых аксиом

По итогам разработок последних пятидесяти лет, связанных с техникой вынуждения и ее применением ко множеству открытых проблем в математике, в настоящий момент существуют буквально тысячи вопросов — практически во всех разделах математики — которые, как было доказано, являются независимыми от ZFC. Сюда входят практически все вопросы относительно структуры несчетных множеств. Можно сказать, что феномен неразрешимости настолько вездесущий, что исследование несчетных множеств оказывается практически невозможным только в рамках ZFC (впрочем, существуют весьма примечательные исключения; см. Shelah 1994).

Это подводит нас к вопросу об истинностном значении высказываний, которые оказываются неразрешимыми в ZFC. Должны ли мы удовлетвориться тем, что они неразрешимы? Имеет ли смысл задаваться вопросом об их истинностном значении? Существует несколько возможных позиций на этот счет. Одна из них — позиция скептика: насчет высказываний, неразрешимых в ZFC, не существует окончательного ответа, они также могут оказаться, по существу, пустыми. Другая позиция весьма широко распространена среди математиков, ее также придерживался Гёдель: неразрешимость всего лишь показывает, что система ZFC слишком слабая, чтобы в ней можно было дать ответ на эти вопросы, а следовательно, нам нужно искать новые аксиомы, и когда мы дополним ими ZFC, то сможем найти ответы на эти вопросы. Такой поиск новых аксиом получил название Программы Гёделя (философские аспекты программы Гёделя см. в Hauser 2006; обзор философских проблем обоснования новых аксиом теории множеств см. в статье о больших кардинальных числах и детерминированности).

Центральный мотив теории множеств, таким образом, связан с поиском и классифицированием новых аксиом. Последние в настоящий момент подпадают под два типа: аксиомы больших кардинальных чисел и аксиомы вынуждения.

Большие кардинальные числа

В рамках ZFC невозможно доказать существование регулярного предельного кардинального κ, поскольку если κ является таким кардинальным числом, тогда Lκ будет моделью ZFC и тогда ZFC доказывала бы собственную непротиворечивость, тем самым противореча второй теореме Гёделя о неполноте. Таким образом, существование регулярного предельного кардинального числа необходимо постулировать в качестве новой аксиомы. Такое кардинальное число называют слабо недостижимым. Если, кроме того, κ является сильным пределом, то есть 2λ<κ для любого кардинального числа λ<κ, тогда κ называют сильно недостижимым. Кардинальное число κ является сильно недостижимым, если и только если оно регулярно и Vκ является моделью ZFC. Если GCH выполняется, тогда всякое слабо недостижимое кардинальное число должно быть сильно недостижимым.

Большие кардинальные числа — это несчетные кардинальные числа, удовлетворяющие некоторым свойствам, которые делают их очень большими, и их существование недоказуемо в ZFC. Первое слабо недостижимое кардинальное число является наименьшим из всех больших кардинальных чисел. Помимо недостижимых кардинальных чисел существует богатое и сложное разнообразие больших кардинальных чисел, формирующих линейную иерархию по принципу наибольшей непротиворечивости, а зачастую - и по принципу наиболее непосредственной выводимости (подробнее см. статью о независимости и больших кардинальных числах).

Чтобы образовать следующее, более мощное свойство больших кардинальных чисел, скажем, что подмножество С бесконечного кардинального числа κ является замкнутым, если всякий предел элементов С также находится в С; и С является неограниченным, если для всякого α<κ существует β∈C больше, чем α. Например, множество предельных ординалов меньших, чем κ, является замкнутым и неограниченным. Кроме того, подмножество S из κ называется стационарным, если оно пересекается с каждым замкнутым незамкнутым подмножеством, входящим в κ. Если κ — регулярное и несчетное множество, тогда множество всех ординалов, меньших, чем κ с конфинальностью ω, является примером стационарного множества. Регулярное кардинальное число называется кардинальным числом Мало (Mahlo), если множество сильно недостижимых кардиналов, меньших, чем κ, является стационарным. Таким образом, первое кардинальное число Мало гораздо больше, чем первое сильно недостижимое кардинальное число, так как существует κ сильно недостижимых кардинальных чисел, меньших, чем κ.

Более мощные свойства больших кардиналов возникают из анализа свойств сильной рефлексивности. Как мы помним, принцип рефлексивности (см. раздел 4), который можно доказать в ZFC, утверждает, что всякое истинное высказывание (то есть всякое высказывание, которое является истинным в V) будет истинным в некотором Vα. Если мы усилим этот принцип за счет его преобразования в высказывание второго порядка, мы получим некоторые большие кардиналы. Например, κ — сильно недостижимое кардинальное число, если и только если всякое высказывание Σ11 (утверждение о существовании второго порядка в языке теории множеств, в котором содержится один дополнительный предикативный символ), истинное в любом структуре вида (Vκ,∈,A), где A⊆Vκ, является истинным в некотором (Vα,∈,A∩Vα), при α<κ. Тот же самый тип рефлексивности, но теперь уже для высказываний Π11 (универсальных высказываний второго порядка), дает куда более мощное свойство большого кардинального числа κ, называемое слабой компактностью. Всякое слабо компактное кардинальное число κ является кардинальным числом Мало, и множество кардинальных чисел Мало, меньших, чем κ, является стационарным. Допуская рефлексию для более сложных высказываний второго или более высокого порядка, мы получаем большие кардинальные числа, которые являются более мощными, чем слабая компактность.

Наиболее известные большие кардинальные числа, которые называют измеримыми, были открыты Станиславом Уламом в 1930 году в ходе решения проблемы меры множества. Мерой множества (двузначной) или ультрафильтром на кардинальном числе κ является подмножество U∈Р(κ), обладающее следующими свойствами: (1) пересечение любых двух элементов U содержится в U; (2) если Х∈U и Y является подмножеством κ, таким что X⊆Y, тогда Y∈U; и (3) для всякого X∈κ, выполняется строгая дизъюнкция: либо X∈U, либо κ–X∈U. Мера множества U называется κ-полной, если всякое пересечение элементов, число которых меньше, чем κ элементов, принадлежащих U, также содержится в U. И мера множества называется непринципиальной, если не существует α<κ, которое принадлежит ко всем элементам U. Кардинальное число κ называется измеримым, если существует мера множества на κ, которая является κ-полной и непринципиальной.

Измеримые кардинальные числа можно описать с помощью элементарного вложения универсума V в некоторый транзитивный класс М. Когда говорят, что такое вложение j:V→M является элементарным, это означает, что j сохраняет истинность, то есть для любой формулы φ(x1,…,xn) языка теории множеств и любой последовательности a1,…,an, высказывание φ(a1,…,an) будет истинным в V, если и только если φ(j(a1),…,j(an)) истинно в М. Получается, что кардинальное число κ измеримо, если и только если существует элементарное вложение j:V→M, причем М — транзитивно, так что κ будет первым ординалом, сдвинутым j, то есть первым ординалом, таким что j(κ)≠κ. Мы будем говорить, что κ — критическая точка на j, и записывать это следующим образом: crit(j)=κ. Вложение j можно вывести из κ-полной непринципиальной меры на κ, используя так называемое построение ультрастепени. И напротив, если j:V→M является элементарным вложением, М — транзитивно и κ=crit(j), тогда множество U={X⊆κ:κ∈j(X)} является κ-полным непринципиальным ультрафильтром на κ. Полученная из j таким образом мера U называется нормальной.

Всякое измеримое кардинальное число κ является слабо компактным, и существует множество слабо компактных кардинальных чисел, меньших чем κ. В действительности, помимо κ существует множество полностью неописуемых кардинальных чисел — это значит, что они отражают все высказывания любой сложности, в языке любого порядка.

Если κ измеримо и j:V→M задается ультрастепенным построением, тогда Vκ⊆M и всякое высказывание меньшей длины, чем κ элементов из М, или равной ей, будет принадлежать М. Таким образом, М во многом схоже с V, но они не могут совпадать. Действительно, знаменитая теорема Кеннета Кунена доказывает, что не существует никакого элементарного вложения j:V→V, помимо тривиального — то есть тождества. Во всех известных доказательствах этого положения используется аксиома выбора, и вопрос о необходимости ее применения является исключительно важным. Благодаря требованию близкого сходства М и V теорема Кунена открывает возможность образования более мощных свойств больших кардинальных чисел, чем измеримость.

Например, κ называют сильным, если для всякого ординала α существует элементарное вложение j:V→M, для некоторого транзитивного М, так что κ=crit(j) и Vα⊆M.

Другое важное и гораздо более мощное свойство кардинальных чисел — это суперкомпактность. Кардинальное число κ называют суперкомпактным, если для всякого α существует элементарное вложение j:V→M с транзитивным М и критической точкой κ, такое что j(κ)>α и всякая последовательность элементов М длиной α принадлежит М.

Кардинальные числа Вудина располагаются между сильными и суперкомпактными. Всякое суперкомпактное кардинальное число является кардинальным числом Вудина, и если δ является кардинальным числом Вудина, тогда Vδ является моделью ZFC, в которой существует собственный класс сильных кардинальных чисел. Таким образом, хотя кардинальное число Вудина δ необязательно должно быть очень сильным само по себе (первое кардинальное число Вудина даже не является слабо компактным), это подразумевает, что в Vδ существует много больших кардинальных чисел.

Помимо суперкомпактных кардинальных чисел мы также находим кардинальные числа Райнхардта, огромные, сверхогромные кардинальные числа и т.д.

Теорема Кунена о несуществовании нетривиального элементарного вложения j:V→V, по сути, показывает, что для любого λ невозможно произвести элементарное вложение j:Vλ+2→Vλ+2, отличное от тождества.

Самые сильные свойства кардинальных чисел, которые, по всей видимости, не противоречат ZFC, формулируются следующим образом:

● Существует элементарное вложение j:Vλ+1→Vλ+1, отличное от тождества.

● Существует элементарное вложение j:L(Vλ+1)→L(Vλ+1), отличное от тождества.

Большие кардиналы образуют линейную иерархию по принципу большей непротиворечивости. В действительности они представляют собой основание иерархии интерпретируемых математических теорий (подробнее см. в статье о независимости и больших кардинальных числах). Для любого высказывания φ выполняется ровно одно из следующих трех положений касательно ZFC и φ:

● ZFC и φ вместе противоречивы.

● ZFC и φ равнонепротиворечиво ZFC.

● ZFC и φ равнонепротиворечиво ZFC и существованию некоторого большого кардинального числа.

Таким образом, большие кардинальные числа могут использоваться для доказательства того, что из данного высказывания φ не выводится другое высказывание Ψ, равное ZFC, за счет доказательства того, что из ZFC вместе с Ψ следует непротиворечивость некоторых больших кардинальных чисел, в то время как из ZFC и φ составляют непротиворечивую систему, если мы допускаем существование меньшее большого кардинального числа или только допускаем, что ZFC непротиворечива. Иными словами, Ψ более непротиворечива, чем φ, равное ZFC. Тогда, согласно второй теореме Гёделя о неполноте, исходя из ZFC и φ нельзя доказать ψ, если мы допускаем, что ZFC и φ составляют непротиворечивую систему.

Как уже было отмечено, в ZFC невозможно доказать существование больших кардинальных чисел. Однако все указывает на то, что их существование не только нельзя опровергнуть, но, в сущности, допущение их существования является весьма обоснованной аксиомой теории множеств. Во-первых, существует множество свидетельств в пользу их непротиворечивости, в частности, для тех больших кардинальных чисел, для которых возможно построить внутреннюю модель.

Внутренние модели больших кардинальных чисел

Внутренняя модель ZFC является транзитивным собственным классом, который содержит все ординалы и удовлетворяет всем аксиомам ZFC. Таким образом, L является наименьшей внутренней моделью, а V — наибольшей. Некоторые большие кардинальные числа, например, недостижимые, слабо компактные или кардинальные числа Мало, могут существовать в L. То есть, если κ обладает одним из таких свойств больших кардинальных чисел, тогда оно также будет обладает этим свойством в L. Однако некоторые большие кардинальные числа не существуют в L. Действительно, Скотт (Scott 1961) показал, что, если существует измеримое кардинальное число κ, тогда V≠L. Важно отметить, что κ не принадлежит L, так как L содержит все ординалы, но оно неизмеримо в L, так как κ-полная непринципиальная мера множества на κ не может существовать в L.

Если κ — измеримое кардинальное число, тогда мы можем построить L-образную модель, в которой κ будет измеримым, за счет применения κ-полной непринципиальной и нормальной меры множества U, примененной к κ, продолжив далее, как в определении L, но теперь используя U в качестве дополнительного предиката. Полученная модель, называемая L[U], будет внутренней моделью ZFC, в которой κ измеримо, причем κ будет единственным измеримым кардинальным числом. Модель является каноничной в том же смысле, что и любая другая нормальная мера множества, свидетельствующая об измеримости κ, производила бы ту же самую модель; она также обладает многими свойствами L. Например, она характеризуется проективной вполне упорядоченностью и удовлетворяет GCH.

Куда сложнее построить аналогичные L-образные модели для более сильных больших кардинальных чисел, таких как сильные кардинальные числа или кардинальные числа Вудина. Это модели вида L[E], где Е — последовательность расширенных систем (extenders), каждая из которых представляет собой систему мер множеств, задающих соответствующие элементарные вложения.

Наибольшие L-образные модели для больших кардинальных чисел, которые были получены на данный момент, могут содержать вудиновы пределы кардинальных чисел Вудина (Neeman 2002). Однако, построение L-образной модели для суперкомпактного кардинального числа все еще проблематично. Граница суперкомпактности, по-видимому, играет ключевую роль, поскольку Вудин смог доказать, что для L-образного типа моделей суперкомпактных кардинальных чисел, которые он называет Ultimate-L, все более сильные большие кардинальные числа, которые могут существовать в V (расширимые, огромные, I1 и т.д.), также будут существовать в этой модели. Построение Ultimate-L пока не доведено до конца, и все еще неясно, будет ли оно завершено, поскольку оно основано на некоторых технических гипотезах, которые нуждаются в подтверждении.

Следствия из существования больших кардинальных чисел

Существование больших кардинальных чисел имеет очень важные следствия, даже для легко определяемых малых множеств, таких как проективные множества, состоящие из действительных чисел. Например, Соловей (Solovay 1970) исходя из допущения о существовании измеримых кардинальных чисел доказал, что все множества Σ12 действительных чисел поддаются мере Лебега и обладают бэровским свойством, что невозможно доказать в ZFC. А Шелах и Вудин (Shelah and Woodin 1990) доказали, что из существования собственного класса кардинальных чисел Вудина следует, что теорию L(R), даже с действительными числами в качестве параметров, невозможно изменить при помощи техники вынуждения, а значит, все множества действительных чисел, принадлежащие L(R), являются регулярными. Далее, в соответствии с более слабой гипотезой о больших кардинальных числах, а именно гипотезой о существовании бесконечного числа кардиналов Вудина, Мартин и Стил (Martin and Steel 1989) смогли доказать, что всякое проективное множество действительных чисел является детерминированным, то есть аксиома PD будет выполняться, следовательно, все проективные множества являются регулярными. Более того, Вудин показал, что из существования бесконечного числа кардиналов Вудина, над которыми стоит измеримое кардинальное число, следует, что любое множество действительных чисел в L(R) является определенным, то есть аксиома ADL(R) будет выполняться, следовательно, все множества действительных чисел, принадлежащие L(R) — а значит, и все проективные множества — являются регулярными. Он также доказал, что кардинальные числа Вудина позволяют сделать оптимальные допущения о больших кардинальных числах, приведя доказательство следующих утверждений:

1. Существует бесконечно много кардинальных чисел Вудина.

2. ADL(R) являются равнонепротиворечивыми, т.е. ZFC + 1 непротиворечиво, если и только если ZFC + 2 непротиворечиво. Подробнее см. в статье о больших кардинальных числах и детерминированности.

Другая область, в которой большие кардинальные числа играют важную роль, связана с возведением в степень сингулярных кардинальных чисел. Так называемая гипотеза сингулярных кардиналов (SCH) полностью детерминирует поведение степеней сингулярных кардинальных чисел по показателям степеней регулярных кардинальных чисел. SCH следует из GCH, а следовательно, выполняется в L. Следствием из SCH является то, что, если 2ℵn<ℵω для всех конечных n, то 2ℵω=ℵω+1. Таким образом, если GCH выполняется для кардинальных чисел, меньших, чем ℵω, тогда она также выполняется для ℵω. SCH выполняется для первого суперкомпактного кардинального числа (Solovay). Но Магидор (Magidor 1977) доказал примечательный факт, что, благодаря допущению существования больших кардинальных чисел, возможно построить такую модель ZFC, в которой GCH не выполняется для ℵω, а следовательно, SCH также не будет выполняться. Для этого требуются большие кардинальные числа, более сильные, чем измеримые. С другой стороны, ZFC достаточно для доказательства того, что если SCH истинна для всех кардинальных чисел, меньших, чем ℵω1, то она также истинна и для ℵω1. Кроме того, если SCH истинна для всех сингулярных кардинальных чисел счетной конфинальности, тогда она будет истинна для всех сингулярных кардинальных чисел (Силвер).

Аксиомы вынуждения

Аксиомы вынуждения — это аксиомы теории множеств, которые утверждают, что некоторые утверждения о существовании теоретико-множественных объектов являются абсолютными между универсумом V всех множеств и его (идеальных) расширений, произведенных за счет процедуры вынуждения, то есть некоторые утверждения о существовании, которые являются истинными для некоторых расширений универсума V, истинны в самом универсуме V. Первая аксиома вынуждения была сформулирована Дональдом Мартином как следствие доказательства непротиворечивости гипотезы Суслина Соловеем и Тенненбаумом; ныне эта аксиома известна как аксиома Мартина (МА). Перед тем как сформулировать ее, скажем, что частичное упорядочение является непустым множеством Р вкупе с бинарным отношением ≤ на Р, которое является рефлексивным и транзитивным. Два элемента множества Р, p и q, называют совместимыми, если существует r∈P, такой что r≤p и r≤q. Антицепь Р является подмножеством Р, элементы которого попарно несовместимы. Частичное упорядочение Р называют ссс, если всякая антицепь Р является счетной. Непустое подмножество G, входящее в Р, называют фильтром, если (1) любые два элемента G совместимы, и (2) если p∈G и p≤q, то q∈G. Наконец, подмножество D, входящее в Р, называют плотным, если для всякого p∈P существует q∈D такое, что q≤p.

МА утверждает следующее:

Для всякого ссс частичного упорядочения Р и любого множества {Dα:α<ω1} плотных подмножеств Р существует фильтр G⊆P, который является родовым для этого множества, то есть G∩Dα≠∅ для всех α<ω1.

Мартин и Соловей (Martin and Solovay 1970) доказали непротиворечивость МА и ZFC применяя видоизмененную технику вынуждения к свойству ссс. На первый взгляд, МА не выглядит как аксиома, то есть не кажется очевидным или по крайней мере вполне обоснованным утверждением о множествах, но, скорее, она напоминает техническое утверждение о ссс частичных упорядочениях. МА, тем не менее, выглядит более естественно, если ее выразить в топологических терминах, ведь она представляет собой простое обобщение хорошо известной теоремы о категории Бэра, в которой говорится, что во всяком компактном хаусдорфовом топологическом пространстве пересечение открытых плотных счетных множеств будет непустым. Действительно, МА равнозначна следующему утверждению:

В любом компактном хаусдорфовом топологическом пространстве ссс пересечение открытых ℵ1-численных плотных множеств будет непустым.

Существует много разных равнозначных формулировок МА; эта аксиома весьма успешно использовалась для разрешения большого числа открытых проблем, существующих в других разделах математики. Например, из нее вытекает гипотеза Суслина и то, что всякое Σ12 множество действительных чисел поддается мере Лебега и обладает бэровским свойством. Из нее также следует, что СН неверна и что 2ℵ0 — регулярное кардинальное число, но невозможно определить исходя из МА, какое это кардинальное число (прочие следствия из МА и ее равнозначных формулировок см. в Fremlin 1984). Несмотря на это, статус МА в качестве аксиомы теории множеств все еще не вполне утвержден. Вероятно, наиболее естественной формулировкой МА, с точки зрения обоснованности, будет формулировка в терминах рефлексивности. МА равнозначна следующему утверждению (где НС обозначает множество наследственно счетных множеств — то есть счетных множеств, элементы которых являются счетными, и элементы подмножеств этих множеств также являются счетными и т.д.):

Для всякого ссс частичного упорядочивания Р, если утверждение о существовании относительно НС истинно в (идеальном) родовом расширении V, достижимом за счет процедуры вынуждения на Р, тогда это утверждение будет истинным, то есть оно будет выполняться в V. Иными словами, если множество, обладающее свойством, которое зависит только от множеств в НС, существует в некотором (идеальном) родовом расширении V, полученным благодаря процедуре вынуждения с ссс частичным упорядочением, тогда множество, обладающее таким свойством, уже существует в V.

Понятие идеального родового расширения V можно уточнить в терминах так называемых булево-значных моделей, которые дают альтернативный способ вынуждения.

Гораздо более сильные аксиомы вынуждения, чем МА, были введены в 1980-е годы, например, аксиома собственного вынуждения Баумгартена (Proper Forcing Axiom, PFA) и более сильный максимум Мартина (ММ) Формана, Магидора и Шелаха (Foreman, Magidor, and Shelah 1988), который, по сути, является наиболее сильной из всех возможных аксиом вынуждения. И PFА, и ММ не противоречат существованию суперкомпактного кардинального числа. PFA утверждает то же, что МА, но для частичного упорядочения, которое обладает более слабым свойством, чем ссс, называемым собственностью (properness; понятие ввел Шелах). ММ выдвигает то же утверждение для более широкого класса частичных упорядочений, которые не разрушают стационарные подмножества ω1 при процедуре вынуждения.

Из сильных аксиом вынуждения, таких как PFA и ММ, вытекает, что все проективные множества действительных чисел являются детерминированными (PD); они также дают множество других важных следствий для бесконечной комбинаторики. В частности, из них следует, что кардинальность континуума равна | | 2.

Библиография

● Коэн, П. Дж., 1969 [1966], Теория множеств и континуум-гипотеза, Москва: Мир.

● Bagaria, J., 2008, “Set Theory”, in The Princeton Companion to Mathematics, edited by Timothy Gowers; June Barrow-Green and Imre Leader, associate editors. Princeton: Princeton University Press.

● Enderton, H.B., 1977, Elements of Set Theory, New York: Academic Press.

● Ferreirós, J., 2007, Labyrinth of Thought: A History of Set Theory and its Role in Modern Mathematics, Second revised edition, Basel: Birkhäuser.

● Foreman, M., M. Magidor, and S. Shelah, 1988, “Martin’s maximum, saturated ideals and non-regular ultrafilters”, Part I, Annals of Mathematics, 127: 1–47.

● Fremlin, D.H., 1984, “Consequences of Martin’s Axiom”, Cambridge tracts in Mathematics #84. Cambridge: Cambridge University Press.

● Gödel, K., 1931, “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I,” Monatshefte für Mathematik Physik, 38: 173–198. English translation in Gödel 1986, 144–195.

● –––, 1938, “The consistency of the axiom of choice and of the generalized continuum hypothesis”, Proceedings of the National Academy of Sciences, U.S.A. 24: 556–557.

● –––, 1986, Collected Works I. Publications 1929–1936, S. Feferman et al. (eds.), Oxford: Oxford University Press.

● Hauser, K., 2006, “Gödel’s program revisited, Part I: The turn to phenomenology”, Bulletin of Symbolic Logic, 12(4): 529–590.

● Jech, T., 2003, Set theory, 3d Edition, New York: Springer.

● Jensen, R.B., 1972, “The fine structure of the constructible hierarchy”, Annals of Mathematical Logic, 4(3): 229–308.

● Kanamori, A., 2003, The Higher Infinite, Second Edition. Springer Monographs in Mathematics, New York: Springer.

● Kechris, A.S., 1995, Classical Descriptive Set Theory, Graduate Texts in Mathematics, New York: Springer Verlag.

● Kunen, K., 1980, Set Theory, An Introduction to Independence Proofs, Amsterdam: North-Holland.

● Levy, A., 1960, “Axiom schemata of strong infinity in axiomatic set theory”, Pacific Journal of Mathematics, 10: 223–238.

● –––, 1979, Basic Set Theory, New York: Springer.

● Magidor, M., 1977, “On the singular cardinals problem, II”, Annals of Mathematics, 106: 514–547.

● Martin, D.A. and R. Solovay, 1970, “Internal Cohen Extensions”, Annals of Mathematical Logic, 2: 143–178.

● Martin, D.A. and J.R. Steel, 1989, “A proof of projective determinacy”, Journal of the American Mathematical Society, 2(1): 71–125.

● Mathias, A.R.D., 2001, “Slim models of Zermelo Set Theory”, Journal of Symbolic Logic, 66: 487–496.

● Neeman, I., 2002, “Inner models in the region of a Woodin limit of Woodin cardinals”, Annals of Pure and Applied Logic, 116: 67–155.

● Scott, D., 1961, “Measurable cardinals and constructible sets”, Bulletin de l’Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques, 9: 521–524.

● Shelah, S., 1994, “Cardinal Arithmetic”, Oxford Logic Guides, 29, New York: The Clarendon Press, Oxford University Press.

● –––, 1998, Proper and improper forcing, 2nd Edition, New York: Springer-Verlag.

● Shelah, S. and W.H. Woodin, 1990, “Large cardinals imply that every reasonably definable set of reals is Lebesgue measurable”, Israel Journal of Mathematics, 70(3): 381–394.

● Solovay, R., 1970, “A model of set theory in which every set of reals is Lebesgue measurable”, Annals of Mathematics, 92: 1–56.

● Solovay, R. and S. Tennenbaum, 1971, “Iterated Cohen extensions and Souslin’s problem”, Annals of Mathematics (2), 94: 201–245.

● Todorcevic, S., 1989, “Partition Problems in Topology”, Contemporary Mathematics, Volume 84. American Mathematical Society.

● Ulam, S., 1930, ‘Zur Masstheorie in der allgemeinen Mengenlehre’, Fundamenta Mathematicae, 16: 140–150.

● Woodin, W.H., 1999, The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, De Gruyter Series in Logic and Its Applications 1, Berlin-New York: Walter de Gruyter.

● –––, 2001, “The Continuum Hypothesis, Part I”, Notices of the AMS, 48(6): 567–576, and “The Continuum Hypothesis, Part II”, Notices of the AMS 48(7): 681–690.

● Zeman, M., 2001, Inner Models and Large Cardinals, De Gruyter Series in Logic and Its Applications 5, Berlin-New York: Walter de Gruyter.

● Zermelo, E., 1908, “Untersuchungen über die Grundlagen der Mengenlehre, I”, Mathematische Annalen 65: 261–281. Reprinted in Zermelo 2010: 189–228, with a facing-page English translation, and an Introduction by Ulrich Felgner (2010). English translation also in van Heijenoort 1967: 201–215.