физика

Поделиться статьей в социальных сетях:

в избранное

Аргумент дырки

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 1 февраля 1999 года; существенно переработано 30 июля 2015 года.

Что такое пространство? Что такое время? Существуют ли они независимо от вещей и процессов, протекающих в них? Или же их существование паразитирует на вещах и процессах? Возможно ли уподобить их полотну, на котором пишет некий художник, и существуют ли они независимо от того, пишет этот художник на них или нет? Или они связаны чем-то наподобие родительского отношения, которое не существует, пока нет родителей и детей? Иными словами, отсутствуют ли пространство и время до существования вещей с пространственными свойствами и процессов, длящихся во времени?

Эти вопросы горячо обсуждаются с давних времен и до сих пор. Аргумент дырки возник, когда эти вопросы были поставлены в контексте современной физики пространства-времени. В данном контексте пространство и время соединяются в единую сущность, пространство-время, и мы исследуем его статус. С одной точки зрения пространство-время представляет собой субстанцию, своего рода вещь, существующую независимо от процессов, происходящих в пространстве-времени. Это пространственно-временной субстанциализм. Аргумент дырки пытается показать, что субстанциализм ведет к неприемлемым заключениям в большом классе пространственно-временных теорий. Субстанциализм требует, чтобы мы приписывали пространству-времени такое огромное количество свойств, что ни наблюдение, ни даже законы самóй теории пространства-времени, относящейся к ним, не могут определить, какие из них верны. Подобная избыточность логически непротиворечива, а также не опровергается опытом. Однако набор скрытых свойств, которые можно приписать пространству-времени, все же должен быть ограничен. Аргумент дырки утверждает, что пространственно-временной субстанциализм нарушает ограничения.

Аргумент дырки опирается на калибровочную свободу в общей теории относительности, то есть на наличие в ней добавочной математической структуры, не имеющей коррелятов в физической реальности. Аргумент дырки предоставляет шаблон для анализа калибровочной свободы в физических теориях. Он показывает невозможность определения добавочной математической структуры с помощью какого-либо априорного или чисто математического правила. Необходимы те или иные физические основания. Аргумент дырки предоставляет два основания, которые можно использовать: верифицируемость — изменения в рассматриваемой добавочной структуре не влияют на параметры, проверяемые наблюдением; детерминизм — законами теории невозможно определить рассматриваемую добавочную структуру.

Аргумент дырки сформулирован Альбертом Эйнштейном в конце 1913 года для несколько иных целей в поиске решений для общей теории относительности. Аргумент обрел новую жизнь и переформулирован в современном контексте «Джоном в кубе» — Джоном Эрманом, Джоном Стейчелем и Джоном Нортоном.

Обзор исторических аспектов аргумента дырки и его значения в философии и физике можно найти в работе Стейчела (Stachel 2014). Она написана на более сложном уровне, чем эта статья.

Современные теории пространства-времени: руководство для начинающих

По сути все современные теории пространства-времени выстраиваются одинаковым образом. Теория постулирует многообразие событий, а затем определяет для них добавочные структуры для представления содержимого пространства-времени. Стандартным примером является общая теория относительности Эйнштейна. В качестве основного среди множества применений аргумента дырки мы рассмотрим самое известное: расширяющиеся вселенные современной релятивистской космологии.

Этот пример показывает основное содержание аргумента дырки. Если его немного углубить, то можно получить более точную и общую формулировку аргумента. Это последовательно проделано в примечаниях к данной статье, предназначенных для читателей с глубокими познаниями в области дифференциальной геометрии и общей теории относительности.

Вот две основы современной релятивистской космологии — многообразие событий и определенные на нем поля.

Многообразие событий. Рассмотрим нашу Вселенную, модель которой пытается создать релятивистская космология. Ее пространство-время — это совокупная целостность всего пространства во все время. События в этом пространстве-времени — это обобщения бесконечно малых точек обычной геометрии пространства. Геометрическая точка в обычной геометрии пространства — просто отдельная точка в пространстве, она не имеет протяженности. Соответственно, событие в пространстве-времени — это отдельная точка в космологическом пространстве в отдельный момент времени.

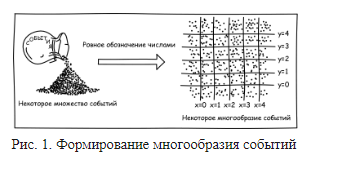
Пока мы определили только множество событий. Чтобы множество событий считалось четырехмерным многообразием, оно должно быть несколько более организованным. В реальном пространстве-времени мы полагаем каждое событие находящимся в некоторой локальной окрестности событий; эта окрестность в свою очередь расположена внутри еще большей окрестности событий и т.д. Подобная дополнительная организация следует из требования возможности гладко отмечать события четырьмя числами или по крайней мере делать это для любого достаточно малого участка многообразия. Отметки образуют систему координат. Из факта достаточности четырех чисел для отметки событий следует четырехмерность многообразия. Теперь мы можем выбирать окрестность некоторого события в виде множества всех точек, чьи пространственно-временные координаты отличаются от нашего исходного события не более чем на одну единицу измерения, две единицы, три единицы и т.д. Таким образом мы получаем вложенные окрестности событий. На рис. 1 показано, как множество событий можно представить в виде двумерного многообразия, присвоив событиям координаты x и y.

Метрическая структура и материальные поля. Хотя мы и определили, что события образуют четырехмерное многообразие, мы еще многого о них не сказали. Мы не указали, какие события лежат в будущем, а какие в прошлом, сколько времени проходит между этими событиями, какие события происходят одновременно и образуют таким образом трехмерные пространства, каковы пространственные расстояния между этими событиями и т.д.

Эти добавочные свойства вводятся посредством задания метрического поля. Чтобы понять, как оно предоставляет эту информацию, представьте все кривые, соединяющие все пары событий в пространстве-времени. Информация о прошедших интервалах времени и пространственных расстояниях задается прошедшими интервалами времени и расстояниями по всем этим кривым. См. рис. 2:

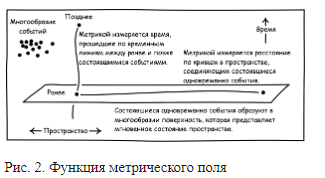
Информацию можно представить в виде огромного каталога, в котором определено пространственное или временное расстояние между каждой парой событий по каждой соединяющей их кривой. Однако такой громадный каталог был бы чрезвычайно избыточен. Если известно расстояние от A до B и от B до C по некоторой кривой, тогда также известно расстояние от A до C. Минимум необходимой нам информации — пространственное и временное расстояние между каждым событием и, грубо говоря, всеми бесконечно близкими к нему событиями. Именно эту информацию предоставляет метрическое поле. Речь идет о «поле», поскольку информация имеет отношение только к одному событию. Затем мы можем воссоздать пространственное и временное расстояние по любой кривой, просто сложив все расстояния между последующими бесконечно близкими друг к другу точками по кривой.

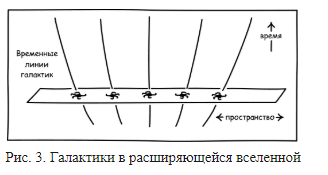
Материя вселенной представлена материальными полями. Простейшую форму материи (большие глыбы, образующие галактики) можно представить мировыми линиями, вычерчивающими во времени историю каждой галактики. В стандартных моделях галактики удаляются друг от друга, и это представлено расхождением галактических мировых линий при переходе к более поздним моментам времени. См. рис. 3:

Свобода общей ковариантности

Когда в 1910-е годы Эйнштейн впервые представил свою общую теорию относительности, ее новым свойством была ее общая ковариантность. Это была первая теория пространства-времени, которая позволяла свободно использовать произвольные системы координат пространства-времени. Данное свойство сейчас используют практически все современные формулировки теорий пространства-времени, включая современные версии специальной теории относительности и ньютоновской теории пространства-времени. В первоначальном виде общая ковариантность понималась «пассивно», то есть как свобода описывать структуры в пространстве-времени средствами произвольно выбранных систем координат. Эта свобода оказалась эквивалентна другой, известной как «активная» общая ковариантность. В соответствии с активной общей ковариантностью мы вправе распространять на многообразие геометрические структуры (наподобие метрических полей) различными способами, число которых определяется существующими преобразованиями координат. (Более подробные сведения о взаимосвязи между активной и пассивной ковариантностью можно найти в дополнительном документе «Активная и пассивная ковариантность».)

Осуществление этой свободы является главной операцией, задействованной в аргументе дырки. Рис. 4 показывает один из способов распространения метрической структуры и материальных полей на многообразие пространственно-временных событий:

На рис. 5 показан второй способ:

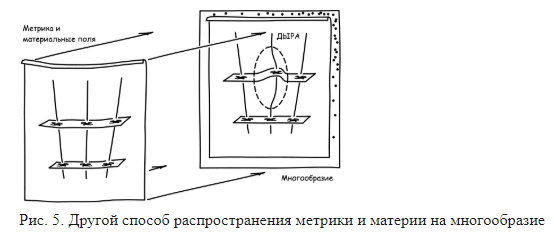
Назовем такое преобразование между двумя распространениями «дырочным преобразованием». Обозначенная пунктиром область — это «дырка». Первое распределение метрики и материальных полей преобразуется во второе таким образом, что

— поля вне дырки остаются неизменными,

— в дыре они распространены по-другому,

— распространения внутри и вне дырки соединяются гладко.

Сохранение инвариантов

Инварианты

У двух разных распространений имеется одна важнейшая характеристика, от которой зависит аргумент дырки: все инвариантные свойства этих двух распространений полностью совпадают.

Инвариантные свойства отличны от неинвариантных. Из неинвариантных свойств наиболее известны те, которые зависят от определенного выбора системы координат. Например, в двумерном евклидовом пространстве только одно событие лежит в начале системы координат, то есть в точке x=0, y=0. Но то, каким событием оно будет, зависит от выбора системы координат. Таким образом, свойство «находиться в точке отсчета» инвариантом не является. Пространственное расстояние между двумя точками остается тем же самым независимо от системы координат, используемой для описания пространства. Это инвариант.

Несмотря на то, что поля в двух случаях распространены по-разному, все их инвариантные свойства совпадают. То есть в отношении инвариантов они одинаковые.

Этот последний результат, по сути, объясняет распространенность общей ковариантности. Законы теории пространства-времени обычно формулировались как отношения между инвариантными свойствами. Следовательно, если им удовлетворяет одно пространство-время, им также должно удовлетворять преобразование этого пространства-времени, обладающее такими же инвариантными геометрическими свойствами, как исходное.

Инварианты и наблюдаемые параметры

Между инвариантами пространственно-временной теории и их наблюдаемыми параметрами, которые подлежат верификации, существует особая связь:

Все наблюдаемые параметры можно свести к инвариантам.

Например, если кто-то путешествует из одной галактики в другую, все связанные с путешествием наблюдаемые параметры будут инвариантами. К ним относятся затраченное на путешествие время, наличие или отсутствие ускорения космического корабля в любой момент времени его путешествия, возраст галактики отбытия в начале путешествия и возраст галактики прибытия в конце путешествия, а также все действия, которые могут быть связаны с передачей сигнала посредством частиц или световых импульсов.

Следовательно, если эти два распространения или распределения метрических и материальных полей при некотором преобразовании с возникновением дырки совпадают по инвариантам, они также совпадают по всем наблюдаемым параметрам. Они неразличимы путем наблюдения.

Что представляет пространство-время? Субстанциализм многообразия

Вернемся к нашей первоначальной задаче: мы хотим узнать, можем ли мы считать пространство-время субстанцией, то есть обладает ли оно независимым существованием. Для этого нам нужно узнать, какие из вышеперечисленных структур представляют пространство-время. Один из наиболее распространенных ответов гласит: пространство-время представляется многообразием событий. Вскоре мы увидим, что именно эта популярная формулировка фигурирует в аргументе дырки. Это естественный выбор, поскольку современные теории пространства-времени строятся на первоначальном постулировании многообразия событий и последующем определении на них добавочных структур. Многообразие играет роль вместилища, чего мы и ожидаем от пространства-времени.

Общая теория относительности делает затруднительным рассмотрение метрического поля просто в качестве части вмещающего пространства-времени. Ведь в дополнение к пространственной и временной информации метрическое поле также представляет гравитационное поле. Поэтому оно также переносит энергию и импульс — энергию и импульс гравитационного поля (хотя пресловутая техническая проблема общей теории относительности препятствует определению энергии и плотности импульса гравитационного поля для любого отдельно взятого события в пространстве-времени). Энергия и импульс свободно сообщаются с другими материальными полями в пространствах-времени. Это, например, источник огромных количеств энергии, высвобождаемых в виде излучения и тепла при коллапсе звезды. Перенос энергии и импульса — естественная отличительная характеристика материи, содержащейся в пространстве-времени. Таким образом, метрическое поле общей теории относительности сопротивляется простому описанию. Нам бы хотелось, чтобы оно было исключительно частью пространственно-временного вместилища или же вмещаемой материи. Однако похоже, что оно должно входить в состав и того, и другого.

Утверждение о том, что многообразие представляет независимо существующую вещь, вполне естественно в рамках реалистического взгляда на физические теории. С этой точки зрения осуществляются попытки буквального толкования физических теорий. Согласно приведенной выше формулировке, пространство-время является многообразием событий с определенными на нем полями. В буквальном понимании это многообразие является независимо существующей структурой, обладающей свойствами.

Издержки пространственно-временного субстанциализма

До сих пор мы характеризовали субстанциалискую позицию как точку зрения, согласно которой пространство-время существует независимо от своего содержимого. Формулировка вызывает мощные, хоть и туманные мысленные образы, однако она недостаточно ясна для интерпретации в контексте физических теорий. Если представлять пространство-время в виде многообразия событий, как описать независимость его существования? Не будет ли контрфактическим заявление о том, что без метрических и материальных полей многообразие событий по-прежнему будет существовать? Этот контрфактуал автоматически отрицается стандартной формулировкой, утверждающей наличие у любого пространства-времени по крайней мере метрической структуры. Такое опровержение субстанциализма многообразия выглядит слишком простым. Несомненно, должна быть лучшая формулировка. К счастью, нет необходимости заниматься ее поиском. Для наших целей достаточно рассмотреть следствие субстанциалистской точки зрения и оставить в стороне задачу ее точного изложения.

В знаменитом споре о пространстве и времени Лейбниц дразнил Кларка, субстанциалиста и представителя точки зрения Ньютона, спрашивая, как изменится мир, если поменять местами Восток и Запад. Для Лейбница никаких изменений не произойдет, потому что все пространственные отношения между телами сохранятся. Но субстанциалист-ньютонианец признавал, что тела мира теперь занимают иные пространственные положения, поэтому две системы физически отличны друг от друга.

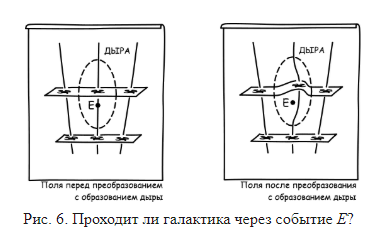
Соответственно, когда мы по-разному распространяем метрические и материальные поля на некоторое многообразие событий, мы разными способами присваиваем метрические и материальные свойства событиям в этом многообразии. Например, представим, что галактика проходит через некоторое событие E в дырке. После дырочного преобразования галактика может не пройти через событие. Для сторонника субстанциализма многообразия это должно составлять объективный физический факт: галактика или проходит через E, или нет. Два распределения представляют две физически различные возможности.

Иначе говоря, сторонники субстанциализма многообразия должны отрицать эквивалентность, выведенную на основе лейбницевской насмешки и названное в его честь:

Эквивалентность Лейбница. Если два распределения полей связаны некоторым гладким преобразованием, они представляют одинаковые физические системы.

Приложение

Визуализация эквивалентности Лейбница с помощью картографических проекций

показывает основную идею эквивалентности Лейбница при помощи аналогии с различными картографическими проекциями поверхности Земли.

Неблагоприятные последствия

Теперь можно собрать все вышесказанное воедино и сформулировать неблагоприятные последствия субстанциализма многообразия. Рассмотрим два распространения метрических и материальных полей, связанные дырочным преобразованием. Поскольку сторонники субстанциализма многообразия отрицают эквивалентность Лейбница, они должны утверждать, что две системы представляют различные физические системы. Однако свойства, отличающие две этих системы, трудноуловимы. Они не поддаются (а) верификации путем наблюдения и (б) детерминации средствами космологической теории.

(а) Верификация путем наблюдения. Мы уже говорили, что эти два распределения неразличимы при наблюдении. Так, сторонники субстанциализма должны настаивать на том, что прохождение или непрохождение галактики через событие E имеет важное физическое значение. Однако ни одно наблюдение не покажет, находимся ли мы в мире, в котором галактика проходит через событие E, или в мире, в котором она проходит мимо него, поскольку в контексте наблюдения вселенные с обоими вариантами эквивалентны.

Из рис. 6 может быть не очень понятно, что два распределения тождественны при наблюдении. В первом распределении слева средняя галактика двигается по тому, что представляется прямой линией, и находится непосредственно в пространственной середине между галактиками с обеих сторон. Во втором распределении справа все выглядит не так. Галактика как будто ускоряется, отклоняясь вправо и приближаясь к галактике справа от нее.

Все показанные на рис. 6 различия являются неинвариантными. Для правого распределения на рисунке галактика меняет направление вправо, но в то же время расстояния между событиями тоже растягиваются, точно так же, как они растягивались на разных картографических проекциях, показанных в дополнительном документе «Визуализация эквивалентности Лейбница с помощью картографических проекций». Итак, галактика всегда остается в пространственной середине для галактик по обеим сторонам. Просто она не выглядит находящейся в пространственной середине из-за того способа, которым нарисована.

Точно так же вектор ускорения по мировой линии галактики определяет, ускоряется ли она. Этот вектор является инвариантом. Так, если галактика в левом распределении имеет нулевой вектор ускорения, то соответствующая галактика в правом распределении также будет иметь нулевой вектор ускорения. Вспомним, что дырочное преобразование сохраняет инварианты. Поэтому если галактика не ускоряется в левом распределении, она также не будет ускоряться в правом.

(b) Детерминизм. Физическая теория релятивистской космологии не может выбрать один из этих двух случаев. Так проявляется индетерминизм теории. Мы можем указать распределение метрических и материальных полей по многообразию событий за исключением области, обозначенной как «Дыра». Теория не способна сказать, какова будет эволюция полей в дырке. И первоначальное, и преобразованное распределение являются полноправными продолжениями метрических и материальных полей вне дырки внутрь дырки, поскольку каждое из них удовлетворяет всем законам теории релятивистской космологии. Теория не имеет средств, позволяющих настаивать на приемлемости лишь одного из распределений.

Важно понимать, что неблагоприятные последствия состоят не только лишь в провале детерминизма. Мы все слишком хорошо знакомы с подобными провалами, и они вовсе не становятся автоматически основанием для игнорирования физической теории. Самым известным примером широко признанной недетерминистской теории является квантовая теория, в стандартной интерпретации которой измерение системы может привести к индетерминистскому коллапсу с одним из множества возможных исходов. Менее известно то, что индетерминистские системы можно разрабатывать и в классической физике. Большинство примеров включает в себя такие странности, как тела, материализующиеся на неограниченной скорости из пространственной бесконечности, называемые «вторженцами из космоса» (space invaders) (Earman 1986a: ch. III; см. также статью про каузальный детерминизм). Или они могут возникать при взаимодействии бесконечно большого числа тел в суперзадаче (см. суперзадачи). Относительно недавно был приведен удивительно простой пример, в котором расположенная на куполе материальная точка после произвольного времени задержки спонтанно приходит в движение в произвольном направлении (Norton 2003: sec. 3).

Проблема провала детерминизма в аргументе дырки заключается не в факте провала, а в том, как он происходит. Если мы отрицаем субстанциализм многообразия и принимаем эквивалентность Лейбница, то вызываемый дырочным преобразованием индетерминизм искореняется. Несмотря на то, что существует бесчисленное множество математически различных эволюций полей внутри дырки в рамках эквивалентности Лейбница, все они физически одинаковы. Другими словами, все же существует единственная эволюция физических полей внутри дырки. А значит, индетерминизм напрямую вытекает из субстанциалистской точки зрения. Точно так же, если мы принимаем эквивалентность Лейбница, то нас более не беспокоит невозможность различить два распределения посредством любых возможных наблюдений. Они являются всего лишь разными математическими описаниями одной и той же физической реальности, и это должно удовлетворять всем наблюдаемым параметрам.

Мы можем нагрузить любую физическую теорию излишними фантомными свойствами, которые нельзя определить посредством наблюдения. Если неразличимость этих свойств для наблюдения не выступает значимым доводом в пользу их ложности, то факт внесения ими индетерминизма в теорию, которая оказывается детерминистской с других точек зрения, при таком раскладе должен оказаться достаточно веским контраргументом. Эти свойства невидимы и для наблюдения, и для теории. Нужно отбросить их, а вместе с ними и любую позицию, требующую их сохранения.

Аргумент в кратком изложении

Итак, аргумент дырки означает следующее:

1. Если имеется два распределения метрических и материальных полей, соотнесенные дырочным преобразованием, то согласно субстанциализму многообразия эти две системы отличаются друг от друга физически.

2. Их физическое отличие выходит за пределы наблюдений и детерминирующих возможностей теории, поскольку:

— Эти два распределения тождественны при наблюдении.

— Законы теории не способны предпочесть одну из двух эволюций полей внутри дырки.

3. Следовательно, субстанциализм многообразия отстаивает безосновательное раздувание нашей физической онтологии, и от этой позиции необходимо отказаться.

История аргумента

Эйнштейн падает в дыру…

Аргумент дырки был придуман Альбертом Эйнштейном в конце 1913 года. Это был акт отчаяния: в поисках формулировки общей теории относительности он столкнулся с тем, что казалось непреодолимыми препятствиями. Годом ранее он был полон решимости создать теорию гравитации, которая обладала бы общей ковариантностью, то есть чьи уравнения оставались бы неизменными при произвольном преобразовании пространственно-временных координат. В том числе он даже рассматривал возможность применения знаменитых уравнений, подчиняющихся принципу общей ковариантности, которые он составит в ноябре 1915 года и которые сегодня приводятся во всех учебниках.

К сожалению, Эйнштейн не понял, что эти уравнения приемлемы. Для слабых гравитационных полей ньютоновская теория гравитации работала практически идеально. Вот почему было очень важно, чтобы в этом случае теория Эйнштейна сводилась к ньютоновской. Однако как он ни старался, Эйнштейн не мог понять, что его уравнения и их многочисленные модификации превосходно сочетаются с теорией Ньютона. В середине 1913 года он опубликовал компромиссное решение: набросок релятивистской теории гравитации, которая не обладала общей ковариантностью. (Подробнее об этих трудностях см. в Norton 1984.)

Неудача в построении приемлемой общековариантной теории сильно беспокоила Эйнштейна. Позднее в 1913 году он нашел способ обратить неудачу в своего рода победу: он решил показать, что вообще ни одна общековариантная теория не является приемлемой. Любая подобная теория нарушала бы закон, который он называл «принципом причинности», а сегодня мы назвали бы его детерминизмом. Он хотел продемонстрировать этот примечательный тезис с помощью аргумента дырки.

В первоначальном изложении аргумента Эйнштейн рассматривал пространство-время, полностью заполненное материей, за исключением одной области, дырки, в которой материя отсутствует. (То есть в первоначальной формулировке «дырка» или «дыра» была более осмысленным термином, чем в современной версии.) Затем он задавался вопросом: будет ли полное определение метрических и материальных полей вне дырки определять метрическое поле внутри нее. Поскольку Эйнштейн неявно избегал эквивалентности Лейбница, он полагал, что отрицательный ответ достаточен для доказательства несостоятельности всех общековариантных теорий.

…и выбирается из нее

Эйнштейн два года упорно трудился над своей ошибочной теорией ограниченной ковариантности. Позднее в 1915 году, когда в конце концов появились доказательства его ошибок, Эйнштейн был практически в отчаянии и близок к тому, чтобы все бросить. Он вернулся к поиску общековариантных уравнений с удвоенной силой, частично подгоняемый тем обстоятельством, что не кто иной, как Давид Гильберт, взялся за анализ его теории. Эйнштейн благополучно закончил работу в ноябре 1915 года, сформулировав свою теорию в общековариантном виде.

Долгое время считалось, что Гильберт обогнал в этом Эйнштейна на пять дней. Новое свидетельство в виде пробного оттиска статьи Гильберта дает основание предположить ошибочность такого мнения. Но что более важно — оно ясно показывает, что Гильберт полагал, подобно Эйнштейну, по крайней мере временно, будто бы аргумент дырки исключает все общековариантные теории, и придерживался этого мнения как минимум в пробных оттисках своей статьи. (См. Corry, Renn and Stachel 1997.)

Хотя Эйнштейн молча отклонил его возражения против общековариантных теорий, он не огласил публично своего мнения о том, в чем же заключалась несостоятельность аргумента дырки. Он наконец сделал это, когда опубликовал «аргумент совпадения точек», как назвал его Джон Стейчел. Этот довод, хорошо известный из эйнштейновского обзора общей теории относительности (Einstein 1916: 117), сводится к защите эквивалентности Лейбница. Эйнштейн утверждает, что физическое содержание теории исчерпывается каталогом разрешаемых ею пространственно-временных совпадений. Например, в теории, описывающей только частицы, совпадения являются точками пересечения мировых линий частиц. Эти совпадения сохраняются при преобразовании полей. Следовательно, две системы полей, для которых возможно взаимное преобразование, имеют одинаковое физическое содержимое; они представляют одну и ту же физическую систему.

В течение многих лет полагалось, что аргумент дырки является тривиальной ошибкой проницательного во всем остальном Эйнштейна. Джон Стейчел в 1980 году определил его крайне нетривиальный характер и представил такое прочтение современному обществу историков и философов физики. (См. также Stachel 1986.) В работе Эрмана и Нортона (Earman and Norton 1987) довод был переработан так, чтобы очевидно ставить пространственно-временной субстанциализм под сомнение. Дальнейшее историческое обсуждение см. в Howard and Norton 1993, Janssen 1999, Klein 1995 и Norton 1987. Доскональное обзорное исследование вопроса представлено в четырехтомной работе Renn 2007.

О принятии и неприятии эйнштейновского аргумента совпадения точек сторонниками логического эмпиризма см. в Giovanelli 2013.

Рецепция аргумента

Существует по крайней мере столько же откликов на аргумент дырки, сколько авторов написало о ней. Некоторые просто соглашаются с тем, что аргумент приводит к неизбежному принятию эквивалентности Лейбница. Они хотят прояснить последствия ее принятия, пытаясь найти единую математическую структуру, которая представляет физическую пространственно-временную систему, а не просто класс эквивалентности взаимно преобразуемых структур, допускаемых эквивалентностью Лейбница. В рамках одной из попыток возникла «алгебра Лейбница» (см. Earman 1989: ch. 9, sec. 9). Стало неочевидно, что такие попытки могут оказаться успешными. Так же как взаимно преобразуемые поля представляют одну и ту же физическую систему, существуют различные, но взаимно преобразуемые алгебры Лейбница с одним и тем же физическим смыслом. Если формализмы многообразий и формализмы алгебр Лейбница взаимно преобразуемы, можно ожидать применимости аргумента дырки также и в последующем формализме в результате перевода. (См. Rynasiewicz 1992.)

Другой подход старается объяснить эквивалентность Лейбница и демонстрирует совместимость общей теории относительности с аргументом дырки посредством индивидуации точек пространства-времени с помощью «наблюдаемых параметров Дирака» и соответствующего соглашения о калибровке (Lusanna and Pauri 2006).

Первоначальный аргумент дырки был сформулирован Эйнштейном в контексте общей теории относительности. Аргумент дырки в формулировке, представленной в работе Earman and Norton 1987, применяется ко всем локальным теориям пространства-времени, и сюда относятся общековариантные формулировки фактически всех известных теорий пространства-времени. Есть мнение, что аргумент заходит слишком далеко и что общая теория относительности отличается от множества других теорий тем, что ее пространственно-временная геометрия динамична и только в таких теориях необходимо проверять аргумент дырки. (См. работы Earman 1989: ch. 9, sec. 5; Stachel 1993; Iftime and Stachel 2006.)

Для критиков аргумент дырки являет собой прекрасную цель. Он состоит из череды допущений, каждое из которых необходимо для прихода к успешному заключению. Довод можно застопорить, отвергнув всего одно из его допущений. Разные авторы искали свидетельства в пользу опровержения каждого из них.

Возможно, самая перспективная из этих атак — та, что требует минимального изменения идей, используемых для формулировки аргумента дырки. Она состоит в предположении, что пространство-время лучше представляется не одним многообразием событий, а более полной структурой, например многообразием событий в сочетании с метрическими свойствами. (См., напр., Hoefer 1996.) Этот переход поддерживается идеей, согласно которой многообразию событий недостает ряда свойств, весьма существенных для пространства-времени. Например, в многообразии событий отсутствует понятие прошлого и будущего, прошедшего времени или пройденного пространственного расстояния. Следовательно, возникает соблазн задать пространство-время как многообразие и добавочную структуру, поддерживающую эти пространственно-временные понятия. В релятивистских космологиях эта добавочная структура будет метрической структурой. Такой отвод аргумента дырки иногда успешен, а иногда нет. В некоторых важных частных случаях можно применять альтернативные версии аргумента дырки против сторонников субстанциализма и использования многообразия в сочетании с добавочной структурой. (См. Norton 1988.)

В более общем смысле мы можем только догадываться, являются ли стоящие перед пространственно-временным субстанциализмом проблемы артефактом описанного выше частного формализма. Бейн (Bain 1998, 2003) исследовал эффект перехода к другим формализмам.

Самый простый контрдовод отмечает, что эквивалентность Лейбница является стандартным допущением в современной физико-математической литературе, и предполагает, что даже допущение его отрицания (к которому должны прибегать сторонники субстанциализма многообразия) является разновидностью математического просчета, на которую не стоит обращать внимание. Хотя принятие эквивалентности Лейбница широко распространено в физической литературе, она не является логической истиной, которую можно опровергнуть только противоречием. То, что она включает нетривиальные допущения, принятие которых требует трезвой оценки, показало первоначальное принятие аргумента дырки Давидом Гильбертом. (См. раздел 8.2 выше.) Если отрицание эквивалентности Лейбница — такой очевидный математический просчет, что ни один компетентный математик не допустит его, то наши стандарты компетенции стали недостижимо высоки, поскольку Давид Гильберт в 1915 году не соответствовал бы им.

Недавно вопрос был заново открыт в Weatherall (forthcoming). Автор утверждает, что взаимно преобразуемые математические структуры, принятые в стандартной математической практике, должны быть одной и той же структурой. Следовательно, они должны представлять одну и ту же физическую систему, препятствуя опровержению эквивалентности Лейбница. Робертс (Roberts 2014) ответил, что решать, являются ли две математические структуры представлениями одной и той же физической системы, должна Природа, а не математическая практика.

Другое направление критики состоит в поиске принципиальных оснований для отрицания общей ковариантности. Один подход пытается доказать, что правильног представить пространство-время можно лишь с помощью одной из двух взаимно преобразуемых систем полей на некотором многообразии. Так, Модлин (Maudlin 1990) утверждает, что каждое событие пространства-времени выступает носителем главным образом своих метрических свойств, то есть перед нами будет не то же самое событие, если (после перераспределения полей) мы попробуем присвоить ему иные метрические свойства. Баттерфилд (Butterfield 1989) описывает взаимно преобразуемые системы как разные возможные миры и использует теорию двойников с тем, чтобы показать, что только один из них может представлять действительное пространство-время.

Вот лишь несколько из огромного числа откликов, изобретательность и техническая глубина которых продолжает расти. При рассмотрении аргумента практически все его аспекты были взвешены и проверены. Является ли индетерминизм аргумента дырки только артефактом неправильно выбранного определения детерминизма? Является ли эта проблема всего лишь тривиальной версией философской загадки непостижимости референции? Или проблема кроется глубоко в физике? Споры по этим и другим вопросам продолжаются. Чтобы ознакомиться с ними, читателю рекомендуется обратиться к библиографии в конце статьи.

Более широкое значение аргумента

Аргумент дырки обрел более широкое значение в философии науки в рамках трех тематических направлений, будучи связанным с реалистической установкой в отношении теоретических объектов, теориями квантовой гравитации и вопросом о том, как следует понимать калибровочную свободу в физических теориях.

Ограничение научного реализма

Аргумент дырки составил новую трудность для развития научного реализма. Согласно этой точке зрения, утверждения наших устоявшихся теорий необходимо понимать буквально. Так, если общая теория относительности описывает многообразие событий и метрическую структуру, то с точки зрения строгих научных реалистов это буквально и есть то, что существует. Считать иначе означало бы, по мнению научных реалистов, что успех теорий следует относить к необъяснимому чуду. Если пространство-время действительно не имеет геометрической структуры, приписываемой ей общей теорией относительности, то как мы можем объяснить ее успешность?

Несмотря на привлекательного данного взгляда, аргумент дырки показывает, что на буквальное прочтение успешной теории должен быть наложен ряд ограничений. Или, по крайней мере, что настаивание на таких прочтениях дорого обходится. Аргумент дырки показывает, что, возможно, стоит допустить существование чего-то менее реального, чем диктуемое буквальным прочтением, иначе мы будем вынуждены постулировать физически реальные свойства, которые выходят за границы и наблюдений, и детерминирующих возможностей нашей теории.

Аргумент дырки и квантование гравитации

Одной из наиболее неподатливых проблем в современной теоретической физике является квантование гравитации. Эйнштейновская общая теория относительности, сформулированная в 1915 году, породила революционно новый подход в мышлении о гравитации в терминах искривления пространства-времени. Однако сейчас признано, что она не может служить окончательным объяснением гравитации. Причина в том, что это все еще классическая теория. Она не рассматривает материю сообразно с квантовой теорией.

Проблема сведения квантовой теории и общей теории относительности в единую теорию остается нерешенной. (См. статью «Квантовая гравитация».) Существует множество претендентов, в первую очередь теория струн и петлевая квантовая гравитация. Одна из проблем заключается в том, что аргумент дырки показал: ни одна успешная теория квантовой гравитации не отказывается от пространства-времени как независимого вместилища. Джон Стейчел был одним из первых приверженцев этого вывода из аргумента дырки (см. Stachel 2005). Эту трудность часто вспоминают теоретики петлевой квантовой гравитации, особенно в контексте критики подходов теории струн, поскольку последние используют такое пространство-время. См. Gaul and Rovelli 1999 и Smolin 2005.

Аргумент дырки как шаблон для анализа калибровочной свободы

В философии физики аргумент дырки способствовал росту осознания важности калибровочных преобразований. Анализ аргумента предоставляет философам физики удобный шаблон при решении вопроса о том, что является калибровочной свободой, а что нет.

Что такое калибровочная свобода?

Чтобы понять, как это работает, сначала рассмотрим, что же такое калибровочная свобода. Калибровочная свобода возникает всякий раз, когда имеются математически различные структуры, представляющие в какой-нибудь физической теории одну и ту же физическую ситуацию. Самый простой и известный пример — ньютоновская теория гравитации. Если имеется некоторая большая масса M, например Солнце, она действует на единичную контрольную массу на расстоянии r от Солнца силой притяжения F, равной

F = GM/r2,

где G — гравитационная постоянная. Эта сила является наблюдаемым параметром в том смысле, что под действием силы единичная контрольная масса на расстоянии r будет двигаться по направлению к основной массе с ускорением F.

Те же самые факты о гравитации можно выразить в терминах поля потенциала U. Большая масса M создает поле потенциала U в удаленной от этой массы точке на расстоянии r в соответствии с

U = −GM/r

Поле потенциала U с уменьшением r становится более отрицательным. Для r= 6, 4, 3, …, U = −2, −3, −4, …, где мы выбрали численно удобный случай GM=12. Поскольку массы передвигаются в области с более низким потенциалом, они попадают в эту отрицательную потенциальную яму.

Простое правило позволяет нам определить силу, затягивающую единичную массу в потенциальную яму. Эта сила — просто отрицательный градиент поля потенциала, где (грубо говоря) градиент представляет собой разность потенциалов рассматриваемой точки и бесконечно близкой точки.

Например, сравним точку на r=10 и r=10,1. Два потенциала имеют достаточно близкие значения U(10)=−0,1, а U(10,1)=−0,099. Их разность равна 0,001. Теперь сравним точку на r=5 и r=5,1. Два потенциала имеют достаточно близкие значения U(5)=−0,2 и U(5,1)=−0,196. Их разность равна 0,004. Соотношение сил равно 0,004/0,001 = 4 = 22. Такого соотношения и следовало ожидать из обратного закона квадратов, который гласит, что обратные квадраты расстояний равны (10/5)2= 22.

Важным моментом здесь является то, что поле потенциала U = −GM/r — только одно из очень многих полей потенциала, подчиняющихся обратному закону квадратов для сил F = GM/r2. Поскольку силы F находятся из поля потенциала U путем сравнения значений U в соседних точках пространства, мы можем везде добавить постоянную, скажем, K, к U и по-прежнему получать те же самые силы. Когда мы сравниваем поле потенциала U в соседних точках, K в каждой точке сокращаются.

Как мы увидим ниже, очень важно, что постоянная K должна оставаться одинаковой везде в пространстве только в один момент времени. Ее значение в разные моменты времени может меняться. Так, в момент времени t=0 может быть K=0, а в момент времени t=1 может быть K=27 и т. д. Чтобы показать, что K может меняться со временем t, но не в пространстве, здесь оно записано как K(t).

Если мы используем свободу, чтобы добавить константу K(t) к полю U и преобразовать его в новое поле потенциала U′, мы приходим к самому простому примеру калибровочного преобразования:

U′ = U + K(t) = −GM/r + K(t)

Оба поля, U и U′, дают одинаковые наблюдаемые силы. Для определения гравитационных сил, действующих на тела, мы можем использовать либо U, либо U′. Не имеет значения, какое поле выбрать. Это означает, что два потенциальных поля U и U′ представляют одинаковую реальность. Преобразование между ними — это калибровочная свобода.

Это самый простой и известный пример калибровочной свободы в физике. Если мы принимаем эквивалентность Лейбница, то дырочное преобразование, связывающее два метрических поля аргумента дырки, является другим примером калибровочного преобразования. Калибровочные преобразования давно стали значимыми в физике частиц: они предоставили мощные средства для создания теорий полей взаимодействия.

Философская проблема калибровочной свободы

Взаимно преобразуемые математические структуры часто встречаются в физических теориях. Философская проблема, связанная с ними, такова: как мы можем узнать, когда две взаимно преобразуемые структуры фактически представляют одну физическую ситуацию, иными словами, как узнать, что преобразование является калибровочным?

Иногда считается, что самого факта взаимной преобразуемости двух математических структур достаточно для того, чтобы считать преобразование калибровочным, а различие между двумя структурами не соотносить с чем-либо физическим. Поскольку преобразование обратимо, очень важно, что любое свойство первой структуры будет иметь коррелирующее свойство во второй и наоборот. Это означает, что две структуры являются, условно говоря, идеальными математическими подобиями друг друга, и одну можно заменять другой в любом формальном применении.

Однако тезис, что это преобразование должно быть калибровочным, неверен. Того факта, что две структуры являются идеальным математическим зеркальным подобием друг друга, недостаточно, чтобы утверждать, что они должны представлять одинаковые физические структуры. Они определенно могут представлять одинаковые структуры, но могут и не представлять. Рассмотрим математическое трехмерное евклидово пространство, которое используется для представления трехмерного физического пространства с евклидовыми свойствами. Математическое пространство содержит множество плоских, двумерных поверхностей, каждая из которых идеально преобразуется в другую. Но сказать, что эти преобразования — только калибровочные преобразования, значит разрушить трехмерность физического пространства и превратить его в двумерное. Все двумерные поверхности в физическом пространстве являются идеальной копией друг друга. Они не являются одной и той же поверхностью. Преобразования между ними нельзя считать калибровочными.

Вот один из основных результатов обсуждения аргумента дырки:

Решение о том, является ли некое преобразование калибровочным, нельзя принять, опираясь только на средства математики. Это физический вопрос, который следует решать исходя из физических соображений.

К сожалению, это усложняет дело. Красивое математическое условие принадлежности к калибровочной свободе было бы прямым решением этой проблемы. Разнообразные физические точки зрения, говорящие в пользу или против калибровочной свободы, более туманны и менее убедительны. Шаблон аргумента дырки предоставляет два показателя того, что рассматриваемое преобразование является калибровочным:

Преобразование может быть калибровочным и не соотноситься с действительными изменениями в представляемой физической реальности, если

а. (невозможность верификации) изменения в математических структурах не проявляются в каких-либо наблюдаемых параметрах;

а. (провал детерминизма) законы теории не способны выбрать одну из двух структур, связанных преобразованием, даже при наличии обширных начальных условий, совпадающих для обеих структур.

Аргумент, который обосновывает этот критерий, совпадает с аргументом дырки, будучи просто несколько более обобщенным. Предположение состоит в том, что добавление математических усовершенствований в математическую трактовку физической теории возможно, если они однозначно не имеют физических аналогов. Признаком того, что мы достигли этой точки физической избыточности, является возможность вносить в математические структуры изменения, не вызывающие различий в наблюдаемых параметрах, а также превосходить детерминирующие возможности законов теории. Когда структуры становятся невидимыми для возможностей наблюдения и законов теории, мы осознаем, что зашли слишком далеко.

Эти идеи можно развивать и далее. Эрман (Earman 2003) обобщает описанный подход и полагает, что ограниченный гамильтонов формализм предоставляет веское основание для установления принадлежности некоторого преобразования к калибровочному типу. (Чтобы узнать о философских проблемах, связанных с калибровочными преобразованиями, ознакомьтесь со статьей о симметрии и нарушении симметрии, особенно с разделом 2.5, а также с работой Brading and Castellani 2003.)

Пример аргумента дырочного типа в теории поля

Провал детерминизма по типу аргумента дырки зачастую можно получить и в теориях поля, конечно же, в зависимости от частных свойств конкретной теории поля. Вот пример из ньютоновской теории гравитации.

Рассмотрим поле вокруг массы, для которой GM=12. Мы должны использовать преобразование

U′ = U + K(t) = −GM/r + K(t),

чтобы создать аргумент дырочного типа, показывающий, что это преобразование является именно калибровочным.

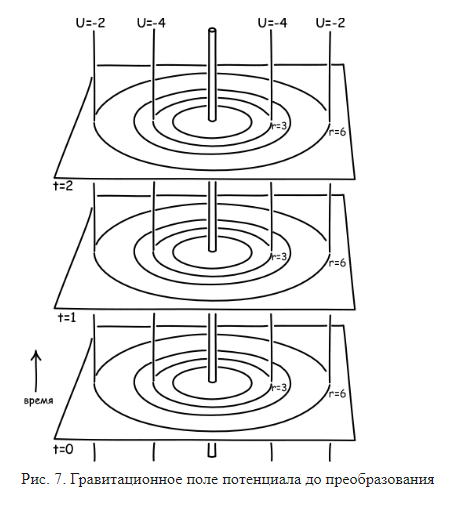
Мы начинаем с поля U. Оно имеет значения U(6)=−2, U(4)=−3, U(3)=−4, U(2)=−6. Если мы предположим, что масса M покоится в пространстве, то поле потенциала U будет постоянно во времени. Это поле изображено на рис. 7. Здесь показано пространство вокруг основной массы в разные моменты времени t=0, t=1 и t=2. Окружности соответствуют точкам в пространстве с одинаковым значением U. Например, на расстоянии r=6 для всех точек U=−2. Постоянство поля во времени представлено вертикальными линиями, которые соединяют точки с одинаковым значением U во времени. Например, точка на расстоянии r=6 в любой момент времени имеет одинаковый потенциал U=−2.

Выберем следующую константу K(t). Она равна 0 для любого момента времени t, кроме интервала 0 < t < 2. В этот временной интервал K(t) растет до максимального значения K(t)=2 в момент времени t=1. Вычисляя поле U′ = U+K(t) для t=1, где K=2, мы находим следующие значения для U′: U(6)=0, U(4)=−1, U(3)=−2, U(2)=−4. На рис. 8 показано это новое поле. В результате преобразования сдвинулись области с определенным значением U′. Например, в моменты времени t=0 и t=2 значение U′=−2 на радиальном расстоянии r=6. Однако в момент времени t=1 U′ имеет другое значение на расстоянии r=6. Точки со значением U′=−2 сдвинулись внутрь на радиальное расстояние r=3. Как и прежде, вертикальные линии соединяют точки с одинаковым потенциалом U′. Они изогнуты внутрь, чтобы отразить сдвиг U′ в интервале времени 0 < t < 2.

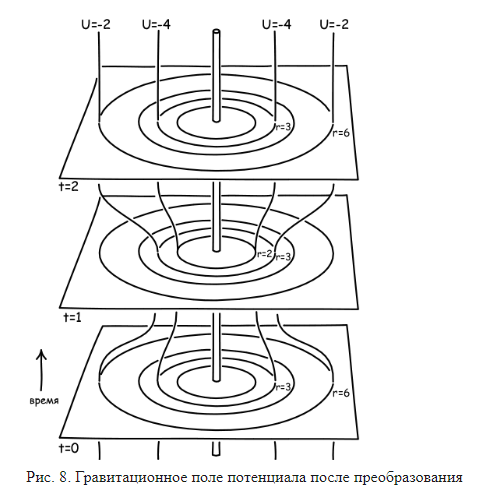
Что же кроется в разности между двумя полями U и U′? Означает ли она какие-либо физические отличия в гравитационных реальностях? Шаблон аргумента дырки предполагает, что нет. Поскольку различие между U и U' не выражает какое-либо различие в верифицируемых путем наблюдения движениях тел, падающих в окрестности массы M, силы в обоих полях одинаковые. Более того, законы ньютоновской гравитационной теории, похоже, не могут различить, какое из двух полей должно быть реализовано в пространстве. Мы можем установить это поле на U=U′ для всего пространства и всех моментов времени в интервалах t < 0,5 и t > 1,5. Тем не менее ньютоновская гравитационная теория не может сказать, какое из полей U и U′ является приемлемым расширением поля потенциала в интервале времени 0,5 < t < 1,5. Любое различие U и U′ в этой области превосходит ньютоновскую теорию гравитации.

В этом примере область, в которой нарушается детерминизм, заполняет все пространство в некоторый короткий период времени. Характерная и беспокоящая особенность индетерминизма первоначального аргумента дырки состояла в том, что индетерминизм был ограничен областью произвольно малого протяжения в пространстве и времени. Подобные невыполнения детерминизма могут возникать в других теориях поля. После калибровочной свободы ньютоновской гравитационной теории наиболее известен пример из классической электродинамики. В ее рамках можно сформулировать аргумент дырки, в котором индетерминизм проявляется в области произвольно малой протяженности в пространстве-времени.

Рынасевич (Rynasiewicz 2012) связал эту калибровочную свободу со свободой, утверждаемой в тезисе об условности одновременности специальной теорией относительности. По его словам, отношение одновременности между удаленными событиями условно в той же степени, в которой физически эквивалентны взаимно преобразуемые модели аргумента дырки.

Больше вариантов использования аргумента по типу дырки см. в следующих работах: Iftime 2006; Healey 1999; Lyre 1999; Rickles 2004, 2005.

Библиография

Bain, Jonathan (1998), Representations of Spacetime: Formalism and Ontological Commitment, Ph.D. Dissertation, Department of History and Philosophy of Science, University of Pittsburgh.

––– (2003), “Einstein Algebras and the Hole Argument,” Philosophy of Science, 70: 1073–1085.

Belot, Gordon (1995), “Indeterminism and Ontology,” International Studies in the Philosophy of Science, 9: 85–101.

––– (1996), Whatever is Never and Nowhere is Not: Space, Time and Ontology in Classical and Quantum Gravity Ph. D. Dissertation, Department of Philosophy, University of Pittsburgh.

––– (1996a), “Why General Relativity Does Need an Interpretation,” Philosophy of Science, 63 (Supplement): S80–S88.

Brighouse, Carolyn (1994), “Spacetime and Holes,” in D. Hull, M. Forbes and R. M. Burian (eds.), PSA 1994, Volume 1, pp. 117–125.

Butterfield, Jeremy (1988), “Albert Einstein meets David Lewis,” in A. Fine and J. Leplin (eds.), PSA 1988, Volume 2, pp. 56–64.

––– (1989), “The Hole Truth,” British Journal for the Philosophy of Science, 40: 1–28.

Brading, Katherine and Castellani, Elena (eds.) (2003), Symmetries in Physics:Philosophical Reflections, Cambridge: Cambridge University Press, pp. 334–345.

Corry, Leo, Renn, Juergen, and Stachel, John (1997), “Belated Decision in the Hilbert-Einstein Priority Dispute,” Science, 278: 1270–73.

Earman, John (1986), “Why Space is not a Substance (At Least Not to First Degree),” Pacific Philosophical Quarterly, 67: 225–244.

––– (1986a), A Primer on Determinism, Dordrecht: Reidel.

––– (1989), World Enough and Space-Time: Absolute Versus Relational Theories of Space and Time, Cambridge, MA: MIT Bradford.

––– (2003), “Tracking down gauge: an ode to the constrained Hamiltonian formalism”, in K. Brading and E. Castellani (eds.), Symmetries in Physics: Philosophical Reflections, Cambridge: Cambridge University Press, pp. 140–162.

Earman, John and Norton, John D. (1987), “What Price Spacetime Substantivalism,” British Journal for the Philosophy of Science, 38: 515–525.

Einstein, Albert (1916), “The Foundation of the General Theory of Relativity,” in H.A. Lorentz et al., The Principle of Relativity, New York: Dover, 1952, pp. 111–164.

Giovanelli, Marco (2013) “Erich Kretschmann as a proto-logical-empiricist: Adventures and misadventures of the point-coincidence argument,” Studies in History and Philosophy of Modern Physics, 44: 115–134.

Healey, Richard (1999), “On the Reality of Gauge Potentials,” Philosophy of Science, 68: 432–55.

Hoefer, Carl and Cartwright, Nancy (1993), “Substantivalism and the Hole Argument,” in J. Earman et al. (eds.), Philosophical Problems of the Internal and External Worlds: Essays on the Philosophy of Adolf Gruenbaum, Pittsburgh: University of Pittsburgh Press/Konstanz: Universitaetsverlag Konstanz, pp. 23–43.

Hoefer, Carl (1996), “The Metaphysics of Space-Time Substantivalism,” Journal of Philosophy, 93: 5–27.

Howard, Don and Norton, John D. (1993), “Out of the Labyrinth? Einstein, Hertz and the Goettingen Answer to the Hole Argument,” in John Earman, Michel Janssen, John D. Norton (eds.), The Attraction of Gravitation: New Studies in History of General Relativity Boston: Birkhäuser, pp. 30–62.

Iftime, Mihaela and Stachel, John (2006), “The hole argument for covariant theories,” General Relativity and Gravitation, 38: 1241–1252.

Janssen, Michel (1999), “Rotation as the Nemesis of Einstein's ‘Entwurf’ Theory,” in Hubert Goenner et al. (eds.), Einstein Studies: Volume 7. The Expanding Worlds of General Relativity, Boston: Birkhaeuser, pp. 127–157.

Jammer, Max (1993), Concepts of Space: The History of Theories of Space in Physics, third enlarged edition, New York: Dover, Chapter 6. “Recent Developments.”

Klein, Martin J. et al. (eds.) (1995), The Collected Papers of Albert Einstein: Volume 4. The Swiss Years: Writing, 1912–1914, Princeton: Princeton University Press.

Lusanna, Luca and Pauri, Massimo (2006) “Explaining Leibniz equivalence as difference of non-inertial appearances: Dis-solution of the Hole Argument and physical individuation of point-events,” Studies in History and Philosophy of Modern Physics, 37: 692–725

Liu, Chuang (1996), “Realism and Spacetime: Of Arguments Against Metaphysical Realism and Manifold Realism,” Philosophia Naturalis, 33: 243–63.

––– (1996a), “Gauge Invariance, Indeterminism, and Symmetry Breaking,” Philosophy of Science, 63 (Supplement): S71–S80.

Leeds, Stephen (1995), “Holes and Determinism: Another Look,” Philosophy of Science, 62: 425–437.

Macdonald, Alan (2001), “Einstein's Hole Argument,” American Journal of Physics, 69: 223–25

Maudlin, Tim (1989), “The Essence of Spacetime,” in A. Fine and J. Leplin (eds.), PSA 1988, Volume 2, pp. 82–91.

––– (1990), “Substances and Spacetimes: What Aristotle Would have Said to Einstein,” Studies in the History and Philosophy of Science, 21: 531–61.

Muller, Fred A. (1995), “Fixing a Hole,” Foundations of Physics Letters, 8: 549–562.

Mundy, Brent (1992), “Spacetime and Isomorphism,” in D. Hull, M. Forbes and K. Okruhlik (eds.), PSA 1992, Volume 1, pp. 515–527.

Norton, John D. (1984), “How Einstein found his Field Equations: 1912–1915,” Historical Studies in the Physical Sciences, 14: 253–316; reprinted in Don Howard and John Stachel (eds.), Einstein and the History of General Relativity: Einstein Studies, Volume 1, Boston: Birkhäuser, 1989, pp. 101–159.

––– (1987), “Einstein, the Hole Argument and the Reality of Space,” in John Forge (ed.), Measurement, Realism and Objectivity, Dordrecht: Reidel, pp. 153–188 .

––– (1988), “The Hole Argument,” in A. Fine and J. Leplin (eds.), PSA 1988, Volume 2, pp. 56–64.

––– (1989), “Coordinates and Covariance: Einstein's view of spacetime and the modern view,” Foundations of Physics, 19: 1215–1263.

––– (1992), “The Physical Content of General Covariance” in J. Eisenstaedt and A. Kox (eds.), Studies in the History of General Relativity: Einstein Studies, Volume 3, Boston: Birkhauser, pp. 281–315.

––– (1992a), “Philosophy of Space and Time,” in M.H. Salmon et al., Introduction to the Philosophy of Science, Englewood Cliffs, NJ: Prentice-Hall; reprinted Hackett Publishing, pp. 179–231.

––– (1993), “General Covariance and the Foundations of General Relativity: Eight Decades of Dispute,” Reports on Progress in Physics, 56: 791–858.

––– (2003), “Causation as Folk Science,” Philosophers' Imprint, 3 (4) [Available Online].

––– (2003a), “General Covariance, Gauge Theories, and the Kretschmann Objection,” in K. Brading and E. Castellani (eds.), Symmetries in Physics: Philosophical Reflections, Cambridge: Cambridge University Press, pp. 110–123.

Renn, Juergen, et al. (eds.) (2007), The Genesis of General Relativity: Sources and Interpretations, (Boston Studies in the Philosophy of Science, Volume 250), 4 Volumes, Berlin: Springer.

Rickles, Dean (2005), “A New Spin on the Hole Argument,” Studies in History and Philosophy of Modern Physcis, 36: 415–34.

Rynasiewicz, Robert (1992), “Rings, Holes and Substantivalism: On the Program of Leibniz Algebras,” Philosophy of Science, 45: 572–89.

––– (1994), “The Lessons of the Hole Argument,” British Journal for the Philosophy of Science, 45: 407–436.

––– (1996), “Is There a Syntactic Solution to the Hole Problem,” Philosophy of Science, 64 (Proceedings): S55–S62.

––– (2012), “Simultaneity, convention, and gauge freedom” Studies in History and Philosophy of Modern Physics, 43: pp.90–94.

Stachel, John (1980), “Einstein's Search for General Covariance,” in Don Howard and John Stachel (eds.), Einstein and the History of General Relativity (Einstein Studies, Volume 1), Boston: Birkhäuser, 1989, pp. 63–100. [This paper was first paper read at the Ninth International Conference on General Relativity and Gravitation, Jena.]

––– (2014) “The Hole Argument and Some Physical and Philosophical Implications,” Living Reviews (Relativity), 17(1): available online.

––– (1986), “What can a Physicist Learn from the Discovery of General Relativity?,” Proceedings of the Fourth Marcel Grossmann Meeting on Recent Developments in General Relativity, R. Ruffini (ed.), Amsterdam: North-Holland, pp. 1857–62.

––– (1993), “The Meaning of General Covariance,” in J. Earman et al. (eds.), Philosophical Problems of the Internal and External Worlds: Essays on the Philosophy of Adolf Gruenbaum, Pittsburgh: University of Pittsburgh Press/Konstanz: Universitaetsverlag Konstanz, pp. 129–160.

Teller, Paul (1991), “Substances, Relations and Arguments About the Nature of Spacetime,” The Philosophical Review, 100 (3): 363–97.

Weatherall, James O. (forthcoming), “Regarding the 'Hole Argument,” British Journal for the Philosophy of Science, preprint available online.

Wilson, Mark (1993), “There's a Hole and a Bucket, Dear Leibniz,” in P. A. French, T. E. Uehling and H. K. Wettstein (eds.), Philosophy of Science, Notre Dame: University of Notre Dame Press, pp. 202–241.