теории

Поделиться статьей в социальных сетях:

в избранное

Теория игр

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 25 января 1997 года; содержательно переработано 9 декабря 2014 года.

Теория игр занимается изучением того, каким образом взаимодействие решений экономических агентов дает результаты сообразно предпочтениям (или полезностям) для агентов, даже если результаты не входили в намерения ни одного из агентов. Значение этого высказывания не будет понятно неспециалистам до тех пор, пока выделенные курсивом слова и фразы не будут объяснены и проиллюстрированы примерами. Этому и будет посвящена настоящая статья. Для начала, однако, мы рассмотрим исторический и философский контекст, дабы подготовить читателя к технической части текста, что последует далее.

Философский и исторический фон

Математическая теория игр была разработана Джоном фон Нейманом и Оскаром Моргенштерном (von Neumann and Morgenstern 1944). По причинам, которые мы обсудим позже, ограничения их математической модели позволяли применять теорию только для ряда специальных и ограниченных условий. За прошедшие семьдесят лет, по мере углубления и обобщения теории, это изменилось самым значительным образом. Теория продолжает дорабатываться, и в конце статьи мы рассмотрим несколько крупных проблем, которые еще только предстоит решить. Однако как минимум с конца 1970-х годов уже можно с уверенностью говорить, что теория игр является самым важным и полезным инструментом в арсенале аналитика, который столкнулся с ситуацией, в которой наилучшее действие агента зависит от его ожиданий от поступков других агентов — а то, что считается наилучшим действием для них, также зависит от их ожиданий по отношению к первому агенту.

Несмотря на то, что теория игр получила математическую и логическую формализацию только в 1944 году, экскурсы в эту область можно найти в античных текстах. Например, в двух сочинениях Платона, «Лахесе» и «Пире», Сократ упоминает сражение при Делии, которое некоторые комментаторы (скорее всего, поздние) интерпретировали следующим образом.

Рассмотрим воина, который готовится вместе со своими товарищами отразить атаку противника. Ему может прийти в голову, что в случае, если оборона окажется успешной, его личный вклад в победу вряд ли будет решающим. Но если он останется в строю, то рискует быть убитым или раненым — как кажется, без всякого смысла. С другой стороны, если противник одержит верх, то шансы нашего воина быть убитым или раненым будут еще выше, что еще более бессмысленно, поскольку оборона все равно будет сломлена. Опираясь на эти соображения, воину, казалось бы, следовало бы дезертировать, независимо от того, кто выиграет битву. Конечно, если все бойцы рассудят так — как им, в общем-то, следовало бы, поскольку они находятся в одной и той же ситуации — это, безусловно, сразу же приведет к поражению в битве. Разумеется, поскольку это очевидно для нас, аналитиков, это может прийти в голову и самим воинам. Дает ли им это основание оставаться в строю? Как раз наоборот: чем больше опасаются воины проиграть сражение, тем больше у них поводов убраться подобру-поздорову. И чем больше их уверенность в победе, которая не требует от них личного участия, тем меньше у них оснований оставаться в строю. Если каждый из них предвосхитит подобный ход мыслей у других, все в итоге быстро впадут в панику, и их командир потерпит поражение прежде, чем враг выпустит первую стрелу.

Задолго до того, как теория игр продемонстрировала аналитикам способы систематического разбора таких проблем, подобные размышления приходили в голову полководцам и влияли на их стратегию. Так, высадившийся в Мексике Кортес имел весьма небольшое войско — и у него были все основания опасаться, что ему не удастся отразить атаки намного более многочисленных ацтеков. Кортес избежал возможного бегства своих войск, предав огню корабли, на которых прибыли испанцы. Не имея физической возможности бежать, у бойцов Кортеса не было лучшего выхода из ситуации, кроме как сражаться — и, более того, сражаться со всей решимостью, на которую они только были способны.

Более того, с точки зрения Кортеса, его действия возымели еще и деморализующий эффект на ацтеков. Он принял специальные меры к тому, чтобы корабли полыхали прямо на глазах у индейцев. И те рассудили так: любой командир, по собственной воле уничтожающий всякую возможность благоразумно ретироваться при неблагоприятном исходе битвы, должен иметь крайне сильные основания для подобного оптимизма. Атаковать врага, имеющего столь весомые причины считать себя непобедимым (какими бы эти причины ни были), неразумно. Потому ацтеки отступили, а Кортес одержал победу, не пролив ни капли крови.

Приведенные выше примеры, битва при Делии и поступок Кортеса, имеют любопытную и при том схожую логическую структуру. Заметьте, что мотивы для дезертирства возникают у солдат не столько потому — или даже только — что они рационально оценивают опасности битвы и свою личную выгону. Скорее, осознавая, что то, что разумно для них, зависит от того, что разумно для других, и что все остальные также могут это заметить, они получают весомые причины для бегства. Даже весьма смелый воин может предпочесть бегство героической, но бессмысленной смерти в попытке единолично остановить наступление противника. Следовательно, мы можем непротиворечиво представить себе обстоятельства, при которых исключительно храбрая армия бежит со всех ног еще до того, как противник двинется в ее сторону.

Другой классический источник, в котором мы находим ту же цепочку рассуждений, — шекспировская пьеса «Генрих V». Во время битвы при Азенкуре Генрих принимает решение казнить пленных французов на виду у врага — и на удивление своих подчиненных, считающих такой поступок аморальным. Основания, из которых исходит Генрих, не имеют отношения к вопросам стратегии: он якобы опасается, что пленники могут освободиться и создать угрозу его позиции. Однако специалист по теории игр мог бы поддержать Генриха со стороны стратегии, хотя его обоснования, будучи благоразумными, возможно, будут не менее аморальны.

Войска увидят казнь пленников, а также то, что ее также лицезрел и их противник. Поэтому они будут знать, какая судьба будет их ждать, если они не одержат победы. Метафорически (но крайне эффективно) выражаясь, их корабли будут преданы огню. Казнь пленников пошлет недвусмысленный сигнал солдатам обеих сторон, и их изменившиеся установки будут благоприятствовать победе англичан.

Эти примеры могут показаться релевантными только для тех, кто регулярно оказывается в ситуации ожесточеннейшей конкуренции. Возможно, подумаете вы, что все это может пригодиться только генералам, политикам, мафиози, тренерам спортивных команд и другим людям, чья работа подразумевает манипулирование другими в стратегических целях — в то время как философу стоит лишь порицать их аморальность. Однако смеем заверить вас, что делать подобные выводы было бы слишком преждевременно. Исследование логики, которая управляет взаимоотношениями между стимулами, стратегическими взаимодействиями и их результатами лежали в основаниях современной политической философии за века до того, как подобному типу логики было найдено имя. Философам в той же мере, что и социологам, необходимо уметь представлять и систематически моделировать не только должное поведение людей, но и их действительное поведение в ситуациях взаимодействия.

«Левиафан» Гоббса часто называют основополагающей работой для современной политической философии. Этот текст положил начало исследованиям функций государственности, ее обоснований, а также ограничений, которые последняя накладывает на индивидуальные свободы. Ключевую мысль Гоббса можно сформулировать довольно прямолинейно: наилучшая ситуация для любого человека — такая, в которой он волен поступать так, как ему вздумается. (Можно с этим соглашаться или не соглашаться, если смотреть на это с точки зрения психологии, но уж такова предпосылка Гоббса.) Зачастую свободные в подобном смысле люди будут стремиться к кооперации для выполнения задач, с которыми невозможно в одиночку. Но если среди них найдется имморальный или аморальный агент, он заметит, что в его интересах будет хотя бы иногда «снимать сливки» с кооперации и не отдавать ничего взамен. Предположим, например, что вы согласились помочь мне с постройкой дома — взамен на мое обещание помочь вам с постройкой вашего. После того, как мой дом возведен, я могу сделать ваш труд неоплачиваемым, просто отказавшись от своего обещания. Потом я, однако, пойму, что если это оставит вас без дома, у вас появится стимул отобрать мой. Это поставит меня в ситуацию постоянного страха, и заставит меня потратить ценные время и ресурсы на защиту от вас. Наилучший способ минимизировать подобные издержки для меня — это ударить первым и убить вас при первой возможности. Конечно же, вы можете предвосхитить все эти рассуждения, происходящие в моей голове, и иметь потому хорошие основания для того чтобы опередить меня. Поскольку я также могу предвосхитить это, мой изначальный страх перед вами не параноидален, равно как и ваши подозрения по отношению ко мне. В действительности, никому из нас не обязательно быть имморальным для того чтобы прийти к подобной цепочке рассуждений; нам достаточно лишь подумать о том, что есть некоторая вероятность, что другой попробует смошенничать. Как только тень сомнения проникает в чей-либо ум, стимул, вырастающий из страха перед последствиями опережающего удара — пострадать от удара до того, как ударил сам — быстро становится чрезвычайно силен. Если хоть один из нас обладает какими-либо небезынтересными для других ресурсами, эта убийственная логика получит власть над нами намного раньше, чем кто-то из нас по глупости предположит, будто мы можем помочь друг другу с постройкой домов. Предоставленные сами себе, хотя бы изредка корыстные агенты будут снова и снова обнаруживать отсутствие всяких выгод от кооперации, вместе с этим все глубже погружаясь в гоббсовскую «войну всех против всех». В подобных обстоятельствах человеческая жизнь, как гласит знаменитая максима Гоббса, действительно будет «одинокой, бедной, мерзкой, грубой и короткой».

Гоббсовским решением этой проблемы стала тирания. Люди могут нанять агента — правительство, которое будет наказывать любого, кто нарушает какое бы то ни было обещание. До тех пор, пока угрожающее наказание будет достаточно тяжелым, потери от нарушения обещаний превысят затраты на их соблюдение. Логика здесь идентична той, которая используется армией, угрожающей расстреливать дезертиров. Если все люди будут четко осознавать, что эти стимулы существуют также и для большинства других, то сотрудничество не просто окажется возможным — оно станет ожидаемой нормой, а война всех против всех сменится общим миром.

Гоббс развертывает логику данного аргумента до очень сильного вывода, утверждая, что он подразумевает не только наличие правительства, обладающего правом и силой для обеспечения сотрудничества, но и «неразделенного» правительства, в котором произвольная воля одного правителя должна налагать абсолютное обязательство на всех. Немногие современные политические теоретики считают, что конкретные шаги, с помощью которых Гоббс приходит к такому выводу, являются одновременно и обоснованными, и правильными. Однако обсуждение этих вопросов увело бы нас от исходной темы и заставило погружаться в нюансы контрактуалистской политической философии. В данном контексте важно то, что эти нюансы, как они обсуждаются в современных дискуссиях, требуют сложной интерпретации проблем с использованием ресурсов современной теории игр. Более того, исходный аргумент Гоббса — что главным обоснованием принудительной власти и практик правительств является потребность людей защищать себя от того, что теоретики игр называют «социальными дилеммами» — принимается многими политическими мыслителями, если не большинством из них. Следует обратить внимание на то, что Гоббс не говорил о желательности тирании как таковой. Согласно его аргументу логика стратегического взаимодействия оставляет только два возможных общих политических решения: тиранию и анархию. Разумные агенты выбирают тиранию как меньшее из двух зол.

Рассуждения афинских солдат, Кортеса и политических агентов Гоббса имеют общую логику, производную от их ситуаций. В каждом случае аспектом окружающей среды, который наиболее важен для достижения агентами предпочтительных для них результатов, является совокупность ожиданий и возможных реакций на их стратегии других агентов. Различие между параметрическим воздействием на пассивный мир и непараметрическим воздействием на мир, пытающийся действовать с опорой на предвосхищение этого воздействия, является фундаментальным. Если вы хотите ударом ноги спустить камень с холма, вам нужно беспокоиться лишь о соотношении массы камня с силой своего удара, степенью сцепления камня с опорной поверхностью, уклоном по другую сторону камня и ожидаемым воздействием удара на вашу ногу. Значения всех этих переменных не зависят от ваших планов и намерений, поскольку глыба не имеет собственных интересов и не предпринимает никаких действий, чтобы попытаться помочь или помешать вам. В отличие от этого, если вы хотите пинком сбросить кого-то с холма, то, если этот человек не находится в бессознательном состоянии, не связан или не беспомощен, вы, скорее всего, не добьетесь успеха, если не сможете замаскировать свои планы, пока ему не станет слишком поздно предпринимать какое-либо упреждающее действие. Более того, можно ожидать, что он попытается как-то отплатить вам, что было бы разумно учитывать. Наконец, относительные вероятности различных его реакций будут зависеть от его ожиданий относительно ваших вероятных ответов на его ответы. (Учитывайте также разницу, которая скажется на обоих ваших рассуждениях, если один или оба из вас вооружены, или один из вас больше другого, или один из вас — начальник другого). Логические проблемы, связанные с ситуацией второго типа (где сталкивают человека, а не камень) обычно намного сложнее, как это проиллюстрирует следующий простой гипотетический пример.

Предположим сначала, что вы хотите пересечь реку, через которую переброшены три моста. (Допустим, что перейти реку вброд, одолеть ее вплавь или переплыть на лодке невозможно) Известно, что первый мост безопасен и скрывает никаких препятствий; если вы попытаетесь пересечь реку по нему, вы добьетесь успеха. Второй мост пролегает под скалой, с которой иногда падают большие камни. Третий кишит смертельными кобрами. Теперь предположим, что вы хотите определить, насколько каждый мост предпочтителен для переправы, и распределить мосты по соответствующим уровням пригодности. Если рисковать своей жизнью вам не по нраву — а как человек мы вполне можете этим наслаждаться (усложнение, которое мы рассмотрим позже в этой статье), — тогда проблема с выбором решения здесь проста. Первый мост, очевидно, лучше всего, так как он безопасен. Чтобы ранжировать два других моста, вам требуется информация об их относительных уровнях опасности. Если бы у вас была возможность некоторое время изучать частоту камнепадов и передвижения кобр, вы смогли бы вычислить, что вероятность быть раздавленным камнями на втором мосту составляет 10%, а быть укушенным коброй на третьем мосту — 20%. Ваше рассуждение здесь строго параметрическое, потому что ни камни, ни кобры не пытаются влиять на ваши действия, например, скрывая типичные закономерности своего поведения в силу того, что они знают, что вы их изучаете. Очевидно, что здесь вам необходимо: пересечь реку по безопасному мосту. Теперь немного усложним ситуацию. Предположим, что мост со скалами находится непосредственно перед вами, в то время как безопасный мост находится на расстоянии сложного суточного перехода. Ваша ситуация с принятием решения здесь немного сложнее, но она по-прежнему остается строго параметрической. Вы должны решить, стоит ли длинный поход 10 % шанса смерти от камнепада. Однако это все, что должны решить именно вы, и вероятность успешной переправы полностью зависит только от вас; окружающую среду не интересуют ваши планы.

Однако, если мы усложним ситуацию, добавив непараметрический элемент, она станет более сложной. Предположим, что вы некий беглец, а на другом береге реки вас ожидает с ружьем ваш преследователь. Он поймает вас и пристрелит, допустим, только если он ждет у моста, который вы пытаетесь пересечь; в противном случае вы убежите. Когда вы рассуждаете о выборе моста, вам приходит в голову, что преследователь также пытается предвидеть ваши рассуждения. Тогда, безусловно, выбор безопасного моста сразу станет ошибочным, так как именно там преследователь и будет вас ожидать, и возможность быть убитым будет несомненной. Поэтому, возможно, вам следует принять риск камнепада, поскольку в этом случае ваш шанс спастись будет намного выше. Однако если вы сможете прийти к такому выводу, ваш преследователь, который так же рационален и хорошо информирован, как и вы, также сможет предвидеть, что вы придете к этому решению (избежать камнепада), и будет ожидать вас именно там, куда вы предпочтете пойти. Поэтому, возможно, вы должны испытать свои шансы с кобрами, поскольку этого преследователь должен ожидать меньше всего. Но тогда… если преследователь ожидает, что вы ожидаете, что он ожидает этого меньше всего, тогда он этого ожидает еще больше всего. Эта дилемма, как вы осознаете с ужасом, является общей: вы должны делать то, чего меньше всего ожидает ваш преследователь; но то, что ваш преследователь будет более всего ожидать именно то, что, по вашим ожиданиям, он бы ожидал менее всего. Похоже, что вы оказались в ловушке неразрешимости. Вас может хоть немного утешить лишь то обстоятельство, что на другом берегу реки ваш преследователь оказывается в ловушке точно такого же затруднения, будучи неспособен решить, у какого моста следует ждать, поскольку как только противник поймет, какое решение вы приняли, он заметит, что если он способен найти наилучшее основание для выбора того или иного моста, то вы можете это предвидеть, и, следовательно, избежать встречи.

Из опыта мы знаем, что в подобных ситуациях люди обычно не остаются в смятении вечно. Как мы увидим позже, существует рациональное решение, — то есть лучшее рациональное действие, — доступное для обоих игроков. Однако до 1940-х годов ни философы, ни экономисты не знали, как найти его математически. В результате экономисты были вынуждены рассматривать непараметрические влияния так, как если бы они были усложненными параметрическими. Это, скорее всего, может показаться странным, поскольку наш пример с переправой должен был показать, что непараметрические функции часто являются фундаментальными особенностями проблем принятия решений. Частично объяснение причин позднего попадания теории игр в эту область заключается в проблемах, с которыми экономисты сталкивались на протяжении истории.

Классические экономисты, такие как Адам Смит и Давид Рикардо, в основном интересовались тем, как агенты на очень больших рынках — целые народы — могут взаимодействовать для обеспечения максимального денежного благосостояния.

Экономисты всегда признавали, что эта совокупность предположений является чистой идеализацией для целей анализа, а не возможным положением вещей, которое любой человек мог бы попробовать (или должен хотеть попробовать) достичь. Но до тех пор, пока математический аппарат теории игр не достиг зрелости к концу 1970-х годов, экономисты вынуждены были надеяться, что чем более рынок приблизится к совершенной конкуренции, тем эффективнее он будет. Однако такая надежда не может быть в целом оправдана ни математически, ни логически; в самом деле, в качестве строгого обобщения данная посылка была признана ложной еще в 1950-х годах.

В этой статье речь не идет об основах экономики, однако нам важно понять истоки и масштабы теории игр, чтобы знать, что в идеально конкурентные рынки встроена некое свойство, которое делает их восприимчивыми к параметрическому анализу. Поскольку агенты не обременены расходами на вход на рынки, они будут открывать магазины на любом рынке, пока конкуренция не обнулит все прибыли. Это подразумевает, что если производственные издержки будут фиксированными, а спрос будет экзогенным, то агенты, — если они пытаются максимизировать разницу между своими расходами и доходами, — не могут свободно выбирать количество производимого. Уровни производства могут быть определены отдельно для каждого агента, поэтому никто не должен обращать внимание на то, что делают другие; каждый агент рассматривает своих коллег в качестве пассивных элементов окружающей среды. Другая ситуация, к которой может применяться классический экономический анализ без использования теории игр, — это монополия со множеством клиентов. Здесь, пока ни один клиент не получит достаточно большой доли спроса для осуществления стратегического влияния, исключаются всякие непараметрические соображения, и задача фирмы заключается только в определении такого сочетания цены и объема производства, при котором она максимизирует прибыль. Тем не менее как идеальная, так и монополистическая конкуренция — это особые и необычные рыночные механизмы. Поэтому до появления теории игр экономисты были существенно ограничены в выборе класса обстоятельств, к которым они могли бы точно применять свои модели.

Философы разделяют с экономистами профессиональный интерес к условиям и методам максимизации благосостояния. Кроме того, философы особенно озабочены логическим обоснованием действий, и зачастую от действий ожидается, что они будут обоснованы в виду ожидаемых от них результатов. (Одна из философских традиций, утилитаризм, отталкивается от идеи, что все могущие быть обоснованными действия должны обосновываться именно таким образом.) Без привлечения теории игр обе эти проблемы ускользают от анализа в ситуациях с непараметрическими аспектами. Мы вскоре продемонстрируем это, ссылаясь на самую известную (хотя и не самую типичную) игровую ситуацию, так называемую «дилемму заключенного», а также на другие, более типичные игры. При этом нам нужно будет ввести, определить и проиллюстрировать основные элементы и методы теории игр. К этому мы теперь и обратимся.

Базовые элементы и допущения теории игр

Полезность

Экономический агент по определению обладает предпочтениями (preferences). Специалисты в области теории игр, подобно экономистам и философам, изучающим рациональное принятие решений, описывают эти предпочтения при помощи абстрактного понятия полезности. Здесь имеется в виду ранжирование по некоторой специфической шкале субъективного благосостояния, которую агент применяет по отношению к тому или иному объекту или событию. Под «благосостоянием» мы понимаем некий нормативный индекс относительного благополучия, который опирается на ту или иную систему отсчета. К примеру, мы можем оценивать относительное благосостояние стран (если мы берем страны в качестве модельных агентов), используя доход на душу населения; мы можем оценивать относительное благосостояние животного — для предсказания и объяснения его поведенческих предрасположенностей — опираясь на наши ожидания относительно его эволюционной приспособленности.

В случае с людьми экономика, равно как и теория игр, обыкновенно оценивает их относительное благосостояние, опираясь на его имплицитную или эксплицитную со стороны самих людей. Поэтому мы выше и говорили о субъективном благополучии. Возьмем человека, который без ума от вкуса маринованных огурцов, но не в восторге от лука. Можно сказать, что он приписывает большую полезность тем состояниям мира, при которых он потребляет больше маринованных огурцов и меньше лука, чем тем, в которых он потребляет больше лука и меньше маринованных огурцов. Примеры подобного рода предполагают, что «полезность» есть мера субъективного психологического удовлетворения.

Именно так это понятие изначально понималось экономистами и философами, испытавшими влияние утилитаризма Иеремии Бентама. Однако в начале ХХ века экономисты со все большей ясностью видели, что предметом их интереса была рыночная собственность, предельный спрос на которую падал, независимо от того, происходило ли это в силу насыщения потребителей или каких-либо еще факторов. В 1930-е годы эта мотивировка экономистов была созвучна бихевиоризму и радикальному эмпиризму в психологии и, соответственно, в философии науки. Бихевиористы и радикальные эмпирицисты протестовали против теоретического использования таких ненаблюдаемых сущностей, как «коэффициент психологического удовлетворения».

Подобный интеллектуальный климат благоприятствовал попыткам экономиста Пола Самуэльсона переопределить полезность, сделав его чисто техническим понятием лишив его спекулятивных психологических корней. В 1950-е годы определение Самуэльсона стало общепринятым: когда мы говорим, что агент действует ради максимизации полезности, под «полезностью» мы понимаем просто Если вы заметили круг в этом определении, вы не ошиблись: теоретики, следующие за Самуэльсоном, действительно рассматривают высказывание «агенты действуют так, чтобы максимизировать полезность» как тавтологию, где «[экономический] агент» — это любая сущность, которая может быть точно описана как действующая для максимизации функции полезности. Под «действием» тут понимается выбор из множества максимизирующих полезность альтернатив, а под «функцией полезности» — то, что экономический агент максимизирует. Подобно всем другим тавтологиям, которые возникают в основаниях научных теорий, эта рекурсивная система дефиниций полезна не сама по себе, но постольку, поскольку позволяет нам установить контекст исследования.

Хотя бихевиоризм 1930-х годов был вытеснен интересом к латентным когнитивным процессам, многие теоретики и по сей день понимают полезность в духе Самуэльсона, поскольку считают важным сохранить применимость теории игр к агентам любого типа — человеку, медведю, пчеле, фирме или стране, — а не только агентам, наделенным человеческим сознанием. Поскольку эти теоретики полагают, что агенты действуют для того чтобы максимизировать полезность, они хотят, чтобы это было частью определения того, что значит быть агентом, а не эмпирическим утверждением о возможных внутренних состояниях и мотивациях. Концепция Самуэльсона, известная как RPT (Revealed Preference Theory, концепция выявленных предпочтений), — которую он описал в своей уже ставшей классической работе (Samuelson 1938), удовлетворяет этому требованию.

Тем, кто интерпретирует теорию игр в терминах RPT, не следует думать о теории игр как об эмпирическом описании мотивов субъектов из плоти и крови (т.е. реальных людей). Скорее, им нужно рассматривать теорию игр как математический аппарат для моделирования сущностей (как существующих, так и нет), которые последовательно выбирают элементы из взаимоисключающих множеств действий. В результате появляются устойчивые паттерны выборов, которые могут быть статистически смоделированы как максимизация функций полезности, с поправкой на стохастичность и шум.

Другие теоретики иначе понимают смысл теории игр. Они рассматривают теорию игр как инструмент, позволяющий описать логику стратегического мышления. Для принятия этой позиции мы должны исходить из того, что агенты в непараметрических ситуациях по крайней мере иногда делают то, что они делают, потому что теоретико-игровая логика рекомендует определенные действия в качестве «рациональных». Такое понимание теории игр включает в себя нормативный аспект, поскольку «рациональность» тут обозначает свойство, которым агент по меньшей мере должен хотеть обладать. Эти два очень общих способа понимания возможного использования теории игр согласуются с тавтологической интерпретацией максимизации полезности по Самуэльсону. Однако это философское различие не является пустым с точки зрения последователей теории игр. Как мы увидим далее в следующем разделе, те, кто надеется использовать теорию игр для объяснения стратегического мышления — в противоположность просто стратегическому поведению — сталкиваются со специфическими философскими и практическими проблемами.

Поскольку теория игр есть технология формального моделирования, нам нужен инструмент, для того чтобы математически мыслить максимизацию полезности. Таким инструментом является функция полезности. Мы введем общую идею функции полезности через ее частный случай, порядковую функцию полезности. (Позже мы встретимся также и с функцией полезности, которая включает в себя больше информации.) Отображение полезности называется «функцией», поскольку она соотносит порядок предпочтений агента с действительными числами. Предположим, что агент х предпочитает набор а набору b, а набор b — набору c. Тогда мы можем сопоставить эти предпочтения с рядом чисел, где функция соотнесет наивысший набор с крупнейшим числом в списке, второй в рейтинге — со вторым числом в списке, и так далее, т.е.:

набор a ≫ 3

набор b ≫ 2

набор c ≫ 1

Единственное свойство, которое зафиксировала эта функция — это порядок. Величины самих чисел неважны; это значит, что мы не должны думать, будто х получит в три раза больше пользы от набора а по сравнению с набором c. Мы можем представить ту же самую функцию полезности так:

набор a ≫ 7 326

набор b ≫ 12,6

набор c ≫ −1 000 000

Числа, которые мы используем в порядковой функции полезности, таким образом, ничего не квантифицируют. Функция полезности, в которой величины этих чисел приобретают значение, именуется «кардинальной». Когда кто-либо говорит о функции полезности, не уточняя, какой именно вид он имеет в виду, вам следует предполагать порядковую функцию. Именно ее мы будем использовать для того, чтобы разобрать наши первые игры. Позже, когда мы начнем говорить о решении игр, которые уже включают в себя рандомизацию — например, игру про переправу и три моста из первой части статьи — нам уже потребуются кардинальные функции полезности. Эту технику описали фон Нейман и Моргенштерн (von Neumann and Morgenstern 1944), и она, собственно, была главной составляющей в изобретенной ими теории игр. Но пока что, однако, нам потребуются только ординальные функции.

Игры и рациональность

Все ситуации, в которых как минимум один агент может максимизировать полезность лишь через предвосхищение (осознанно или нет) реакции одного или более агентов, называются игрой. Агенты, принимающие участие в игре, называются игроками. Если у всех агентов есть оптимальные действия, которые не зависят от поступков других, подобно параметрическим ситуациям, или условиям монополии, или идеальной конкуренции (см. раздел 1), мы можем смоделировать эту игру без обращения к теории игр; в иных же случаях нам без нее не обойтись.

Специалисты в теории игр исходят из того, игроки обладают способностью, которое в экономической литературе обычно именуют «рациональностью». Как правило, это формулируется в виде простых утверждений вроде «предполагается, что игроки рациональны». В критической литературе, как правило, или в случаях применения теории игр в гуманитарных дисциплинах, подобная риторика становится объектом нападок. В западной культурной традиции сеть референций термина «рациональность» крайне плотна и сложна, и сам термин зачастую использовался для того, чтобы с точки зрения нормативности маргинализировать такие обыкновенные и важные свойства как эмоции, женственность и эмпатия. Специалисты в области теории игр используют это понятия, как правило, вынося за скобки его идеологические коннотации. Для наших целей мы будем использовать термин «экономическая рациональность» как строго технический, и не нормативный, который отсылает к узкому и специфическому набору ограничений на предпочтения, с которыми имеют дело (1) изначальная версия теории игр фон Неймана и Моргенштерна и (2) концепция выявленных предпочтений (RPT).

Когда экономисты занимаются моделированием рынков, они также используют другое, не менее важное (для них) понятие рациональности — понятие «рациональных ожиданий». В этой фразе «рациональность» относится не к ограничениям предпочтений, но к не-ограничениям на обработку информации: рациональные ожидания — это идеализированные убеждения, являющиеся продуктом статистически верно взвешенного использования всей доступной агенту информации. Читатель должен иметь в виду, что два эти словоупотребления в рамках одной и той же дисциплины не связаны технически.

Более того, оригинальная RPT в течение этих лет уточнялась различными аксиомами для нужд моделирования. Как только мы начинаем рассматривать рациональность как техническое понятие, то каждый раз, вводя новые аксиомы, мы изменяем и понятие. Следовательно, в любой дискуссии, вовлекающей и экономистов, и философов, мы можем обнаружить, что все используют одно и то же слово, при этом имея в виду совершенно разные вещи. Это вызывает определенные трудности для тех, кому в новинку экономика, теория игр, теория принятия решений и философия действия.

В этой статье термин «экономическая рациональность» будет использоваться в техническом значении, которое он принимает в рамках теории игр, микроэкономики и формальной теории принятия решений, соответственно. Экономически рациональный игрок есть тот, кто может

(1) оценить результаты игры, т.е. ранжировать их по отношению к их вкладу в его благосостояние;

(2) вычислить пути достижения этих результатов, т.е. установить, какая последовательность действий вероятностно связана с соответствующим результатом; и

(3) выделить из набора альтернативных действий (это мы назовем «выбором» действия) такие, что приводят к наиболее предпочтительному результату, при этом учитывая действия других игроков.

Мы можем подытожить лежащую в основании этих рассуждений интуицию следующим образом: ту или иную сущность имеет смысл рассматривать в качестве экономически рационального агента до тех пор, пока у нее есть альтернативы и она выбирает из них, руководствуясь тем, что кажется ей наилучшим для ее целей — и это верно для нее чаще, чем обратное. (Для читателей, знакомых с работами Дэниела Деннета, мы можем сравнить идею экономически рационального агента с сущностями, которые Деннет описывает как интенциональные, и добавить, что мы можем предсказать поведение экономически рационального агента с опорой на интенциональную установку.)

Экономическая рациональность может в некоторых случаях достигаться лишь за счет внутренних вычислений агента, причем ему не обязательно осознавать, что он вычисляет или вычислил их условия и импликации. В других случаях экономическая рациональность может воплощаться в поведенческих установках, возникших в ходе естественного, культурного или рыночного отбора. Поэтому называя действие «выбранным», мы не обязательно подразумеваем, что этот выбор был свободным и осознанным. Мы просто имеем в виду, что действие было предпринято при наличии иной доступной альтернативы, где «доступность» понимается как нечто, что можно выяснить чисто аналитически. (Термин «доступное», когда его используют специалисты в теории игр, не должен пониматься как «метафизическая» или «логическая» доступность; почти всегда доступность следует понимать прагматически, контекстуально и предполагать возможность ее бесконечного пересмотра в ходе все более точного моделирования.)

Каждый игрок выбирает между как минимум двумя стратегиями. Стратегия — это предопределенная «программа игры», которая сообщает игроку, какие действия предпринимать в ответ на любую возможную стратегию, которую только могут использовать другие игроки. Значение фразы, выделенной курсивом, прояснится, когда мы приведем некоторые примеры игр.

Критически важный аспект спецификации игры касается объема информации, которым располагают игроки при выборе стратегии. Простейшие игры (с точки зрения их логической структуры) суть те, в которых агенты располагают полной информацией: то есть в каждый момент, когда стратегия требует от игрока предпринять некоторое действие, он знает всё то, что происходило в игре до этого момента. Настольная игра с последовательными ходами, в которой оба игрока видят все действия и в целом знают правила игры — типа шахмат — является примером простейшей игры. В то время как игра с переправой по мостам из первого раздела является примером игры с неполной информацией, поскольку беглец должен выбрать мост для переправы, не зная, какой мост избрал для засады его преследователь; а последний, соответственно, принимает решение, не зная о выборе своей жертвы. Поскольку теория игр имеет дело с экономически рациональным действиями, принимая во внимание стратегически значимые действия других игроков, вас не должен удивлять тот факт, что то, что думают, или во что не верят, игроки о действиях других, имеет большое значение для нашего анализа. Мы это далее еще увидим.

Деревья и матрицы

Разница между играми с полной и неполной информацией связана с различием между способами репрезентации игр, которые опираются на очередность игры (хотя и не тождественна этому различию). Давайте начнем с того, что установим различие между играми с последовательными и одновременными ходами (речь идет об информации). При первом приближении, кажется естественным полагать, что в игре с последовательным ходом игроки определяются со своей стратегией по очереди, а в игре с одновременным ходом игроки определяются со стратегиями одновременно. Однако это не совсем верно, поскольку стратегическое значение имеет не темпоральный порядок событий как таковой, но то, знают ли игроки — и когда они узнают — о действиях других игроков на момент совершения выбора. Например, если два конкурирующих друг с другом предприятия планируют свои маркетинговые кампании, одно из них может выбрать свою стратегию за месяцы до второго; но если ни одна из сторон не знает, что именно предприняла вторая (или предпримет, когда примет решение) — это игра с одновременным ходом. В шахматы же, напротив, обычно играют как в игру с последовательной очередностью хода: вы видите, что сделал ваш оппонент, прежде чем выбрать свое следующее действие. (Шахматы могут стать игрой с одновременным ходом, если каждый из игроков будет объявлять свой ход на общей доске, будучи изолирован от другого; но эта игра будет сильно отличаться от обычных шахмат.)

Выше было сказано, что различие между играми с последовательным и одновременным ходом не тождественны различию между играми с полной и неполной информацией. Хороший способ уточнить оба концепта — объяснить, почему это так. Как мы говорили выше, игры с одновременным ходом являются играми с неполной информацией. Однако некоторые игры могут быть смесью игр с одновременным и последовательным ходом. Например, две фирмы могут приступить к реализации своих маркетинговых стратегий независимо и в тайне друг от друга — но затем вступить в ценовую конкуренцию, где их действия будут полностью видимы. Если бы оптимальные маркетинговые стратегии частично или полностью зависели от того, что игроки ожидают от дальнейшего противостояния цен, тогда оба этапа необходимо было бы анализировать как единую игру, в которой этап последовательных ходов сменялся бы этапом игры с одновременным ходом. Целые игры, которые включают в себя смешанные этапы подобного рода, являются играми с неполной информацией, даже если и некоторые из ее этапов могут разыгрываться поочередно. Игры с полной информацией, как и подразумевает их название, суть ситуации, где нет одновременных ходов (и где ни один из игроков никогда не забывает о том, что было прежде).

Как мы уже упомянули выше, игры с полной информацией — это простейший, с точки зрения логики, вид игр. Игроки и аналитики в подобных играх (до тех пор, пока они конечны, т.е. заканчиваются после определенного количества действий) могут использовать прямые процедуры для предсказания итогов. Игрок выбирает свое первое действие, учитывая возможные реакции оппонентов на него и контрдействия, что будут доступны ему в дальнейшем. В этом случае он задается вопросом о том, какой из доступных конечных результатов ему наиболее полезен, и выбирает тот ход, который должен быть первым в цепочке событий, приводящей к этому результату. Этот процесс называется обратной индукцией (поскольку рассуждение идет обратно, от конечных результатов к моменту выбора).

Об обратной индукции и ее характеристиках будет мы будет говорить подробнее в следующем разделе, при обсуждении равновесия и выбора равновесия. Пока что мы упомянули ее лишь для того, чтобы с ее помощью представить один из двух типов математических объектов, которые используются для репрезентации игр: игровых деревьев. Игровое древо — это пример того, что математики называют ориентированным графом (или, кратко, орграфом). Он представляет собой множество вершин, связанных таким образом, что граф целиком имеет направление. Мы можем строить деревья сверху вниз или слева направо. В первом случае вершины наверху рассматриваются как более ранние поступки. Если же мы строим наш граф слева направо, то хронологически более ранние события мы размещаем левее. Неразмеченное древо имеет подобную структуру:

Репрезентация игр при помощи деревьев удобна для того, чтобы визуализировать обратную индукцию. Представьте, что игрок (или аналитик) начинает на том краю дерева, где отображены все возможные результаты игры, а потом двигается в обратном направлении, пытаясь определить стратегии, которые к ним приводят.

Поскольку функция полезности для игрока указывает на предпочтительные для него результаты, мы также знаем, какой путь он изберет. Конечно, не все из этих путей будут доступны, поскольку другой игрок также участвует в выборе пути и не будет совершать действия, которые ведут к менее желательным результатам. Мы рассмотрим примеры развития игры в ходе подобных интеракций и детально разберем техники рассуждения на этих примерах после того, как опишем ситуацию, для моделирования которой мы можем использовать деревья.

Деревья используются для репрезентации последовательных игр, поскольку показывают порядок действий игроков. Однако игры иногда изображаются на матрицах, а не деревьях. Это второй тип математических объектов, которые используются для репрезентации игр. Матрицы, в отличие от деревьев, просто показывают результаты — представленные в терминах функции полезности — каждой возможной комбинации стратегий игроков. Например, можно отобразить игру с переправой через реку из первого раздела на матрице, поскольку в этой игре и у беглеца, и у преследователя есть только один ход, и оба игрока принимают свое решение, не зная, какое решение примет другой. Соответственно, вот часть матрицы:

Доступные беглецу стратегии: перейти по безопасному мосту, пойти на риск быть раздавленным камнями или риск быть искусанным кобрами — мы отобразим на соответствующих строках матрицы. Соответственно, на столбцах отобразим опции преследователя — ждать на безопасном посту, ждать на каменистом мосту и ждать на мосту с кобрами. Каждая из ячеек матрицы показывает — или, скорее покажет, как только наша матрица заполнится — результаты в терминах выигрыша, которую придется понести игрокам. Выигрыш для игрока — это просто число, присваиваемое порядковой функцией полезности положению дел, соответствующих результатам игры.

Для каждого результата выигрыш Строки всегда отображается до выигрыша Столбца. Так, например, верхний левый угол нашей матрицы показывает, что если беглец переправляется через реку по безопасному мосту, а преследователь его там ожидает, то выигрыш беглеца 0, а преследователя 1. Мы интерпретируем выигрыши через функции полезности игроков, которые в этой игры очень просты. Если беглец безопасно перебирается через реку, он зарабатывает 1, если нет, то 0. Если беглец не справится с переправой, потому ли, что его пристрелит охотник, завалит камнями или укусит кобра, охотник зарабатывает 1, а беглец 0.

Мы коротко пройдемся по заполненным ячейкам матрицы, а потом объясним, почему мы пока не можем заполнить остальные ячейки. Когда преследователь встречает беглеца на мосту, который последний избрал для переправы, беглец гибнет. Все эти результаты приводят к вектору выигрышей (0,1). Вы можете видеть его по диагонали, пересекающей матрицу с левого верхнего угла по правый нижний. Когда беглец выбирает безопасный мост, а преследователь ждет его на каком-то другом, беглец успешно переправляется через реку — а мы получаем вектор (1,0). Эти результаты отображены во всех оставшихся двух ячейках верхней строки. Все остальные ячейки пока что заполнены вопросительными знаками. Почему? Дело в том, что если беглец выбирает мост с камнепадами или кобрами, он вводит в игру параметрические факторы. В этих случаях он рискует быть убитым и прийти к развязке типа (0,1) независимо от выбора преследователя. А нам пока не хватает понятий для того, чтобы корректно отобразить эти результаты при помощи функций полезности — но вскоре они у нас появятся, и это даст нам ключ для решения трудности, обсуждавшийся в разделе 1.

Матричные игры обычно называют «нормальной формы игры» или «стратегической формы игры», а древовидные игры называют «развернутой формой игры». Эти типы игр не эквивалентны, поскольку в играх развернутой формы есть информация, которой нет в играх стратегической формы — это информация о последовательности ходов в игре и объеме знания игроков о структуре самой игры. В целом, игры стратегической форм могут репрезентировать любую из игр развернутой формы, так что стратегическую форму можно рассматривать в качестве множества игр развернутой формы. Когда порядок ходов не имеет значения для результата игры, вам следует рассматривать стратегическую форму игры, поскольку она содержит все то, о котором вам стоит беспокоиться. Когда же порядок ходов важен, развернутая форма строго необходима, в противном случае ваши выводы будут ненадежны.

Дилемма заключенного как пример представления игры в стратегической и развернутой форме

Различия, описанные выше, сложно понять, если опираться только на абстрактные описания. Лучше всего проиллюстрировать их примером. Для этого мы возьмем самую известную изо всех игр: дилемму заключенного. Она позволяет проиллюстрировать логику проблемы Кортеса и солдат Генри V из первого раздела, а также гоббсовских людей до момента создания Левиафана.

Однако по причинам, которые станут вам ясны позже, не стоит воспринимать дилемму заключенного (ДЗ) как типичную игру: она таковой не является. Мы используем ее в качестве развернутого примера тут только потому, что она хорошо подходит для иллюстрации отношений между стратегической и развернутой формами игр, а позже — для иллюстрации отношений между однократными и повторяющимися играми (см. часть 4 ниже).

Своим названием эта игра обязана ситуации, которой обычно ее иллюстрируют. Предположим, что полицейские задерживают двух людей, которых подозревают в совершении вооруженного ограбления. Однако у правоохранителей нет доказательной базы для того, чтобы предъявить задержанным обвинение в суде. Однако у них достаточно доказательств для того, чтобы упрятать каждого из них за решетку за угон машины. Поэтому следователь делает каждому заключенному следующее предложение: если тот чистосердечно сознается в ограблении и даст показания против своего сообщника, а второй откажется признать свою вину, то первый выйдет на свободу, а второй получит десять лет тюрьмы. Если признательные показания дадут оба, то каждый получит по 5 лет. Но если же оба изберут хранить молчание, то получат по два года за угон.

Первый шаг в моделировании игры с двумя заключенными — представить ситуацию с помощью функции полезности. Следуя традиции, назовем заключенных «Игрок 1» и «Игрок 2». Для обоих игроков порядковая функция полезности одинакова:

Свобода ≫ 4

2 года ≫ 3

5 лет ≫ 3

10 лет ≫ 0

Числа в вышеприведенной функции нам нужны для выражения выигрыша каждого игрока при различных возможных результатах в данной ситуации. Мы можем изобразить их проблему на матрице, которая описывает, как взаимодействуют отдельные варианты — это их игра в стратегической форме:

Каждая из ячеек матрицы отображает выигрыш каждого игрока для каждой комбинации действий. Выигрыш Игрока I — первое число в каждой паре, Игрока II — второе. Итак, если оба игрока дадут показания, то каждый выиграет 2 очка (5 лет тюрьмы). Мы видим это в верхней левой ячейке нашей матрицы. Если ни один из них не даст показаний, то каждый выиграет по 3 очка (два года тюрьмы). Мы видим это в нижней правой ячейке. Если Игрок I дает показания, а игрок II нет, Игрок I выигрывает со счетом 4,0 (свобода против десяти лет заключения), что можно видеть в верхней правой ячейке. Обратная ситуация, в которой Игрок II признается, а Игрок I молчит — в нижней левой ячейке.

Каждый игрок оценивает здесь два доступных ему действия, сравнивая свои личные выигрыши в каждом столбце — это позволяет им судить, какое из действий предпочтительнее, предпочтительнее для них, относительно каждого возможного действия их партнера. Если Игрок II даст показания, то Игрок I получает 2 очка за свои показания и 0 в случае молчания. Если Игрок II молчит, то Игрок I получает 4 очка за показания и 3 за молчание. Поэтому Игроку I лучше признаться, независимо от того, что сделает Игрок II.

Игрок II, тем временем, сравнивает свои выигрыши по каждой строке и приходит к точно такому же выводу, что и Игрок I. Везде, где конкретное действие игрока превосходит все другие для каждого возможного действия оппонента, мы говорим, что первое действие строго доминирует над вторым. В ДЗ признание строго доминирует над молчанием для обоих игроков. Оба игрока понимают это и тем самым полностью отбрасывают искушение отклониться от строго доминируемого пути. Соответственно, они оба признаются — и оба сядут в тюрьму на 5 лет.

Игроки, равно как и аналитики, могут предсказать подобный итог, используя механическую процедуру, известную как последовательное исключение строго доминируемых стратегий. Первый игрок, изучив матрицу, может увидеть, что его выигрыш в каждой ячейке первой строки выше, чем его выигрыш в ячейках строкой ниже. Следовательно, игра по нижнему ряду (т.е. хранение молчания) не может максимизировать его полезность, независимо от того, что делает второй игрок. Поскольку первый игрок никогда не будет использовать стратегию по нижней строке, мы можем просто удалить нижнюю строку из матрицы. Теперь очевидно, что второй игрок не будет отказываться от признания, поскольку его выигрыш от признания в двух оставшихся ячейках выше, чем выигрыш от молчания. Так что теперь мы можем удалить правый столбец из игры. У нас осталась только одна ячейка, которая соответствует обоюдному признанию вины.

Поскольку рассуждение, которое привело нас к исключению всех остальных возможных результатов, на каждом шаге отталкивалось от предпосылки, что оба игрока экономически рациональны — иными словами, мы выбирали стратегии, которые приводили к более высокому выигрышу по сравнению с другими — у нас есть сильные основания рассматривать взаимное признание вины как решение игры, т.е. результат, к которому она должна прийти, если экономическая рациональность является корректной моделью для поведения игроков. Стоит отметить, что порядок удаления строго доминируемых строк и столбцов неважен. Если бы мы сначала удалили правый столбец, а потом нижнюю строку, мы бы пришли к тому же решению.

Мы уже неоднократно говорили о том, что дилемма заключенного во многих отношениях нетипична. Так, все ее столбцы или строки или строго или строго доминируемые, или строго доминирующие. Для любой игры в стратегической форме верно, что последовательное исключение строго доминируемых стратегий гарантированно приведет вас к уникальному решению. Однако, как мы покажем позже, для многих игр это условие не применяется, и решение нашей аналитической задачи становится менее прямолинейным.

Читатель, возможно, заметил нечто тревожащее в результатах игры заключенных. Если бы оба игрока решили хранить молчание, они бы пришли к результату в нижней правой ячейке, при котором оба бы получили лишь два года тюрьмы, и, соответственно, больше полезности, чем в случае признания. Это самый важный аспект ДЗ, и в теории игр он довольно распространен. Мы вернемся к этому, когда будем обсуждать равновесные состояния. Пока что, однако, давайте продолжим рассматривать разницу между играми в стратегической и развернутой форме.

Когда дилемму заключенного выносят на суд неспециалистов, часто можно услышать, что следователю нужно развести подозреваемых по разным камерам, чтобы они не могли общаться друг с другом. Причины тому кажутся самоочевидными: если бы игроки могли общаться, они бы увидели, что им обоим выгодно хранить молчание, и, соответственно, договорились бы об этом, не так ли? Может показаться, что это позволит игрокам избавиться от убеждения в необходимости сознаться, опережая возможное предательство другого. В действительности же эта интуиция обманчива, а вывод из нее ложен.

Когда мы рассматриваем дилемму заключенного как игру в стратегической форме, мы неявно предполагаем, что заключенные не могут прийти к взаимовыгодному соглашению, поскольку они выбирают свои действия одновременно. В этом случае предварительная договоренность никак им не помогает. Если первый игрок убежден, что его партнер будет придерживаться условий сделки, он может воспользоваться возможностью выйти на свободу, дав показания. Конечно же, он поймет, что то же самое искушение встанет и перед вторым игроком; и в этом случае он тем более должен будет признаться, дабы избежать наихудшего для себя исхода. Соглашение заключенных ни к чему не приводит оттого, что у них нет способа принудить друг друга к его исполнению; их данные друг другу обещания представляют собой то, что теоретики игр называют «пустым разговором».

Но теперь предположим, что заключенные принимают решения не одновременно. То есть предположим, что игрок II может сделать выбор после наблюдения за действиями игрока I. Это та ситуация, которую люди, уверенные в необходимости отсутствия коммуникации, должны иметь в виду. Теперь игрок II сможет увидеть, что игрок I остался непоколебим, когда дело дошло до выбора игроком I, и ему не следует беспокоиться о том, что его обманут. Однако это ничего не меняет, лучше всего повторно представить игру в развернутой форме. Это позволит нам ввести деревья игры и соответствующий им метод анализа.

Прежде всего, рассмотрим определения основных понятий, которые будут полезны при анализе игровых деревьев:

Вершина: точка, в которой игрок принимает решение.

Начальная вершина: точка, в которой происходит первое действие игры.

Терминальная вершина: любая вершина, достижение которой оканчивает игру. Каждой терминальной вершине соответствует результат.

Подыгра: любое связанное множество вершин и разбиений, отходящих из одной единственной вершины.

Выигрыш: количество порядковой полезности, которую игрок извлекает из того или иного результата.

Результат: приписывание множества выигрышей, по одному на каждого игрока в игре.

Стратегия: программа, предписывающая игроку, какое действие следует совершать на каждой из вершин игрового древа, где он может сделать выбор.

Эти краткие определения могут быть не очень ясны до тех пор, пока вы не начнете их использовать по ходу нашего анализа деревьев. Вам, пожалуй, лучше всего возвращаться к этому списку, пока мы будем обсуждать примеры. К тому времени, как вы разберетесь с каждым из примеров, эти понятия и их значение станут для вас интуитивно ясны.

Чтобы сделать это упражнение максимально поучительным, давайте предположим, что заключенные изучили нашу матрицу и, увидев, что для них обоих наилучшим является результат из нижней правой ячейки, заключили соглашение о сотрудничестве. Первый игрок должен сохранить молчание первым, после чего второй поступит также, когда полиция попросит его сделать выбор. Мы назовем стратегию соблюдения соглашения «сотрудничеством» и пометим его на дереве ниже литерой «С» (от «cooperation»). Стратегию же нарушения договора мы назовем «отступничеством» и обозначим его литерой «D» (от «defection»). Каждая вершина пронумерована 1, 2, 3, …, сверху вниз, для удобства использования в обсуждении.

Итак, вот наше дерево:

Давайте взглянем на терминальные вершины (они расположены внизу). Они отражают возможные результаты. Каждая из них связана с раздачей выигрышей: как и при игре в стратегической форме, сначала указан выигрыш первого игрока, затем второго. Каждая из структур, что берет начало в вершинах 1, 2 и 3, является подыгрой.

Мы начнем наш обратно-индуктивный анализ с подыгр, которые возникают последними в игре — и будем использовать технику алгоритма Цермело. В подыгре, начинающейся от вершины 3, второй игрок должен выбрать между выигрышем 4 и 3 очков. (Обратите внимание на второе число, обозначающее выигрыш второго игрока в каждом множестве на терминальной вершине, спускающейся от вершины 3). Второй игрок выигрывает больше, играя D. Поэтому мы можем заменить всю подыгру назначением выигрыша (0,4) непосредственно вершине 3, так как именно этот результат будет реализован, если игра достигнет этой вершины.

Теперь рассмотрим подыгру, берущую начало от вершины 2. Здесь второй игрок выбирает между 2 и одним из нулей. Он получит более высокий выигрыш, играя D. Мы можем поэтому присвоить выигрыш (2,2) непосредственно вершине 2. Теперь мы переходим к подыгре, идущей от вершины 1. (Эта подыгра, конечно, тождественна самой игре; все игры являются подыграми самих себя). Теперь первый игрок выбирает между результатами (2,2) и (0,4). Сравнив первые числа в каждом из этих множеств, он видит, что, играя D, он получает более высокий выигрыш — 2. D — это значит дать показания. Таким образом, первый игрок дает показания, а затем их дает и второй, приводя нас к тому же результату, что и при игре в стратегической форме.

Интуитивно ясно, что произошло: первый игрок понял, что если он сыграет C (промолчит) в вершине 1, тогда второй сможет максимизировать свою полезность, предав его и сыграв D. (На дереве это происходит на вершине 3). Это оставляет первого игрока с выигрышем 0 (десять лет в тюрьме), чего он может избежать, только с самого начала играя D. Поэтому он нарушает соглашение.

Таким образом, мы видим, что в случае дилеммы заключенного, будь она игрой хоть с одновременным, хоть с последовательным ходом, обе версии дают один и тот же результат. Однако в других играх это не всегда так. Кроме того, с помощью алгоритма Цермело можно решать только (последовательные) игры с полной информацией в развернутой форме.

Как мы уже упоминали в этой главе, иногда мы должны представлять одновременные действия внутри игр с последовательной очередностью хода на всех остальных этапах. (Во всех таких случаях игра в целом будет игрой с неполной информацией, поэтому мы не сможем ее решить с помощью алгоритма Цермело). Мы представляем такие игры с использованием информационных множеств. Рассмотрим следующее дерево:

Овал, нарисованный вокруг вершин b и c, указывает, что они принадлежат одному информационному множеству. Это означает, что на этих вершинах игроки не могут отследить путь, который их сюда привел. При выборе стратегии игрок II не знает, находится ли он в b или c. (По этой причине в развернутых играх фактически нумеруются информационные множества, которые понимаются как «точки действия», а не сами вершины — поэтому вершины внутри овала обозначены буквами, а не цифрами). Иначе говоря, игрок II, делая свой выбор, не знает, что сделал первый на вершине a. Как вы помните, именно это определяет два хода как одновременные. Таким образом, мы можем видеть, что метод представления игр на деревьях является полностью общим. Если ни одна вершина после начальной не принадлежит отдельному информационному множеству на своем дереве, то в игре есть только одна подыгра (она сама), а вся игра является одновременной. Если хотя бы одна вершина принадлежит тому же информационному множеству, что и какая-либо другая, в то время как все остальные остаются обособленными, то наша игра включает в себя как одновременные, так и последовательные ходы и по-прежнему остается игрой с неполной информацией. Игра с полной информацией имеет место лишь тогда, когда все информационные множества содержат только одну вершину.

Концепции решения и равновесие

Результат, обозначенный нами как (2,2) в дилемме заключенного и соответствующий взаимному предательству, был назван «решением» игры. Следуя принятой в экономике практике, специалисты в области теории игр именуют решения игр равновесиями. Философски подкованные читатели наверняка захотят задать концептуальный вопрос: что именно «уравновешивается» в результатах игр, позволяя нам, таким образом, называть их «решениями»? Когда мы говорим, что физическая система находится в равновесии, мы имеем в виду, что она находится в устойчивом состоянии, при котором все каузальные силы внутри системы уравновешивают друг друга и таким образом оставляют систему «в покое» до тех пор, пока в нее не проникнет некая экзогенная (т. е. внешняя) сила. Именно это традиционно имеют в виду экономисты, когда говорят о «равновесии»; они рассматривают экономические системы точно так же, как и физические: как совокупности взаимно ограничивающих (часто каузальных) отношений. Равновесия таких систем являются их эндогенно стабильными состояниями. (Следует отметить: бывает так, что эндогенно стабильные состояния для некоторых физических, так и экономических систем оказываются недоступны прямому наблюдению, поскольку никогда не бывают изолированы от экзогенных воздействий, что смещают и дестабилизируют их. В классической механике, как и в экономике, понятия равновесия используются в качестве инструментов анализа, а не предсказаний относительно того, что мы ожидаем как наблюдатели). Как мы увидим в последующих разделах, мы можем пользоваться таким пониманием равновесия в теории игр.

Однако, как мы отметили в разделе 2.1, некоторые рассматривают теорию игр как теорию, объясняющую стратегическое мышление. Для них решением игры должен быть результат, который рациональный агент мог бы предсказать, опираясь только на средства рационального вычисления. Для таких теоретиков затруднения, связанные с концепциями решения не так важны, как для тех, кто не пытается использовать теорию игр в качестве вспомогательного инструмента в рамках общего анализа рациональности. Но интерес философов к теории игр чаще всего вызван именно этим стремлением, в отличие от интереса экономистов и других ученых.

Полезно начать наше обсуждение, вернувшись к дилемме заключенного, ввиду ее необычайной простоты с точки зрения проблем с концепциями решения. То, что мы назвали тогда «решением», было уникальным равновесием Нэша для этой игры (названо в честь Джона Нэша, математика, лауреата премии по экономике памяти А. Нобеля, очень много сделавшего для расширения и обобщения новаторской работы фон Неймана и Моргенштерна в Nash 1950).

Равновесие Нэша (далее «РН») применяется к наборам стратегий, по набору для каждого участника игры. Набор стратегий — это РН в том случае, если ни один игрок уже не может, сменив стратегию и учтя стратегии своих партнеров по игре, увеличить свой выигрыш. Обратите внимание на то, насколько близка эта идея идее строгого доминирования: никакая стратегия не может быть РН-стратегией, если она строго доминируема. Поэтому, если последовательное исключение строго доминируемых стратегий приводит нас к уникальному результату, мы знаем, что этот вектор приводит к уникальному РН. Сейчас почти все теоретики согласны с тем, что избегание строго доминируемых стратегий является минимальным требованием к агенту, который претендует на экономическую рациональность. Игрок, который сознательно выбирает строго доминируемую стратегию, прямо нарушает пункт (iii) определения экономической агентности из раздела 2.2. Это означает, что если игра имеет результат, который является уникальным РН — как в случае обоюдной дачи показаний в дилемме заключенного, — он должен быть ее уникальным решением. Это одна из самых главных причин, по которой дилемма заключенного является «легкой» (и нетипичной) игрой.

Мы можем указать еще один класс игр, в котором РН всегда не только необходимая, но и достаточная концепция решения. Это конечные игры с совершенной информацией и нулевой суммой. Игра с нулевой суммой (в случае игры с участием всего двух игроков) — это игра, в которой игрок не может улучшить свое положение, не ухудшив положение другого (простейший пример тут — крестики-нолики: любой ход, который приближает одного игрока к победе, приближает противника к проигрышу, и наоборот).

Мы можем определить, является ли некая игра игрой с нулевой суммой, изучив функции полезности игроков: в играх с нулевой суммой они будут зеркальными отображениями друг друга, а результатам с высоким рейтингом для одного игрока будут соответствовать результатам с низким рейтингом для другого, и наоборот.

В такой игре, если я разыгрываю стратегию, при которой, с учетом вашей стратегии, я не могу сделать ничего лучше, и если вы также разыгрываете подобную стратегию, то, поскольку предпринятая мной смена стратегии должна поставить вас в худшее положение и наоборот, наша игра не может иметь никакого решения, совместимого с нашей общей экономической рациональностью, отличной от ее уникального РН.

Иначе говоря, в игре с нулевой суммой моя стратегия, максимизирующая мой минимальный выигрыш, если вы играете наилучшим возможным образом и одновременно делаете то же самое, просто эквивалентна применению наших наилучших стратегий. Поэтому эта пара так называемых «максимин» процедур гарантировано приводит к уникальному решению игры, которое одновременно будет его уникальным РН. (В крестиках-ноликах это просто ничья: ни вы, ни я не можем получить ничего больше ничьей, если мы оба пытаемся победить и стремимся не проиграть.)

Однако большинство игр не обладают этим свойством. В этой статье невозможно перечислить все типы затруднений, делающие игру проблематичной с точки зрения возможных решений. (Во-первых, крайне маловероятно даже то, что теоретики уже нашли всех возможные проблемы). Однако мы можем попытаться рассмотреть это все немного обобщенно.

Во-первых, есть проблема с тем, что большинство игр с ненулевой суммой имеют больше одного РН, но не все РН выглядят одинаково удовлетворительными решениями для стратегически осмотрительных игроков. Взгляните на игру в стратегической форме (взято из Kreps 1990: 403):

В этой игре есть два РН: s1-t1 и s2-t2. (Следует обратить внимание на то, что ни одна строка или столбец не являются здесь строго доминируемыми, но если I играет s1, то II не может сделать ничего лучше t1, и наоборот; то же верно и для пары s2-t2). Если РН — это наша единственная концепция решения, то мы будем вынуждены признать, что любой из этих результатов в равной степени убедителен в качестве решения. Однако, если теория игр рассматривается как объяснительная и/или нормативная теория стратегического мышления, то видно, что тут чего-то не хватает: не сойдутся ли рассудительные и полностью информированные игроки на s1-t1? (Заметьте, что это не похоже на ситуацию с дилеммой заключенного, в которой социально наилучшая ситуация недостижима, поскольку не является РН. А в игре выше у обоих игроков есть все основания стремиться сойтись на РН, которое для них выгодно).

Это иллюстрирует тот факт, что РН является относительно (с точки зрения логики) слабой концепцией решения, часто не способной предсказать интуитивно разумные решения, применение одного лишь РН не позволяет игрокам использовать принципы равновесного выбора, которые если и не обязательны с точки зрения экономической рациональности (или какой-ли еще более философски амбициозной концепции рациональности), то по меньшей мере представляются как разумными, так и вычислимыми. Рассмотрим другой пример (Kreps 1990: 397):

Здесь ни одна стратегия не доминирует строго над другой. Однако s1 слабо доминирует над s2, так как I преуспевает по меньшей мере в той же степени, разыгрывая s1 вместо s2 для любого хода II, и выигрывает больше, если II отвечает ходом t2. Так не следует ли игрокам (и аналитикам) просто удалить слабо доминируемую строку s2? Если сделать это, то t1 станет строго доминируемым, а РН s1-t2 остается единственным решением.

Однако, как показывает на этом примере Крепс, у идеи, что слабо доминируемая стратегия должна удаляться так же, как и строго доминируемая, есть любопытные последствия. Давайте немного изменим выигрыши игры:

s2 по-прежнему слабо доминируема; но из двух нэшевский равновесий вариант s2-t1 теперь становится наиболее привлекательным для обоих игроков. Так почему же аналитику исключать эту возможность? (Обратите внимание, что эта игра, опять же, не воспроизводит логику из дилеммы заключенных. Там у исключения наиболее привлекательного результата, молчания, есть смысл, поскольку у обоих игроков есть стимулы для одностороннего отказа от него, так что там мы имеем дело не с РН. Но в случае с s2-t1 в настоящей игре это не так. Вы уже начинаете понимать, почему мы назвали игру заключенных «атипичной»?).

Аргумент в пользу исключения слабо доминируемых стратегий такой: что игрок I может нервничать, опасаясь, что игрок II не обязательно экономически рационален (или II боится, что I может оказаться не рационален экономически, или II переживает, что I опасается того, что II не рационален… и так далее до бесконечности), и поэтому есть некоторая вероятность, что II сыграет t2. Если всерьез принимать возможность того, что игрок может не быть экономически рационален, то у нас появляется аргумент в пользу устранения слабо доминируемых стратегий: игрок I таким образом страхуется от наихудшего для себя результата, s2-t2. Конечно, страхуясь подобным образом, он кое-что теряет, уменьшая свой ожидаемый выигрыш с 10 до 5. С другой стороны, мы можем представить, что игроки поговорили перед игрой и договорились разыгрывать коррелированные стратегии, чтобы сойтись на s2-t1, тем самым устраняя неопределенность, которой вызвано желание исключить слабо доминируемую строку s1 и вместо этого исключить s1-t2 из ряда вероятных решений!

Любой предлагаемый принцип решения игр, который позволил бы нам отбросить одно или несколько РН в качестве возможных решений, называется рафинированием РН. В рассматриваемом случае устранение слабо доминируемых стратегий является одним из возможных рафинирований, поскольку оно исключает РН s2-t1, а корреляция — другим рафинированием, поскольку вместо этого она очищает другое РН, s1-t2. Итак, какое рафинирование является более подходящим в качестве концепции решения? Те, кто рассматривает теорию игры как объяснительную и / или нормативную теорию стратегической рациональности, создали немалый корпус литературы, где обсуждаются достоинства и недостатки большого количества рафинирований. В принципе, нет никаких ограничений на количество возможных рафинирований, так как не может быть никаких ограничений на количество возможных философских позиций относительно того, какими принципами могут или не могут руководствоваться рациональные заинтересованные стороны, либо иметь опасения или ожидания или уверенность в отношении того, каким принципам следуют другие игроки.

Теперь мы ненадолго отвлечемся, чтобы сделать терминологическое замечание. В предыдущих изданиях настоящей статьи мы называли теоретиков, предпочитающих интерпретацию функций полезности в духе RPT, «бихевиористами». Термин подчеркивал, что подход RPT приравнивает выбор к экономически последовательным действиям, а не обращается к ментальным конструктам. Однако это словоупотребление, вероятно, вызовет путаницу из-за недавно вошедшей в моду поведенческой теории игр Колина Камерера (Camerer 2003). Эта исследовательская программа пытается ввести в модели теории игр обобщения, выведенные главным образом из экспериментов с людьми: выводы, которые люди делают из наличной информации, оказываются отличными от тех, которые бы сделали экономические агенты («фрейминг»). Применения теории Камерера также обычно содержат специфические предположения о функциях полезности, также опирающиеся на экспериментальные данные. Например, можно предполагать, что игроки готовы идти на компромиссы между неравенством в распределении выигрышей среди игроков и объемом собственного выигрыша. Мы обсудим поведенческую теории игр в разделах 8.1, 8.2 и 8.3. Пока же обратите внимание, насколько важно для подобного использования теории игр предположение, что психологические представления о ценности едины для всех людей. Потому было бы неверно ссылаться на поведенческую теорию игр как бихевиористскую. Но именование традиционной экономической теории, опирающейся на выявленные предпочтения, «бихевиористской» теорией, создает ненужную путаницу. Поэтому мы будем впредь называть конвенциональную теорию «непсихологической» теорией игр. Под этим мы подразумеваем теорию игр, используемую большинством экономистов, которые при этом не занимаются поведенческой экономикой. Они рассматривают теорию игр как абстрактную математику стратегического взаимодействия, а не как попытку описания особых психологических диспозиций, возможно, типичных для людей.

Специалисты в непсихологической теории игр склонны скептически оценивать большую часть уточнений, привносимых поведенческой теорией игр. Это с очевидностью вызвано тем, что она полагается на интуиции о том, какие выводы люди должны считать разумными. Как и большинство ученых, теоретики непсихологических игр скептически оценивают силу и основания каких бы то ни было философских допущений, взятых в качестве ориентира для эмпирического и математического моделирования.

Однако поведенческую теорию игр можно понимать и иначе: как уточнение теории игр, не обязательно затрагивающее ее концепции решения. Она ограничивает базовые аксиомы теории, чтобы применять ее к особому классу агентов — психологически типичных людей. Ограничение нужно для работы с суждениями и предпочтениями, которые люди находят естественными, независимо от того, кажутся они рациональными или нет (а они зачастую ими не являются). Непсихологическая и поведенческая теории игр едины в том, что ни одна из них не является нормативной — хотя обе они часто используются для описания норм, преобладающих в группах игроков, а также объяснения того, почему нормы могут оставаться неизменными в группах игроков, даже если они оказываются менее рациональными с философской точки зрения. Обе теории, полагают, что задача прикладной теории игр состоит в предсказании результатов эмпирических игр при заданном распределении стратегических диспозиций и распределении ожиданий относительно стратегических диспозиций других игроков, которые оформляются изменениями в окружении игроков, включая институциональное давление, структуры и эволюционный отбор. Поэтому мы объединим исследователей непсихологической и поведенческой теорий игр в группу дескриптивистов лишь затем, чтобы противопоставить их нормативным теоретикам игр.

Дескриптивисты часто склонны сомневаться в том, в поисках общей теории рациональности есть какой-либо смысл. Институты и эволюционные процессы создают множество самых разнообразных условий, и то, что считается рациональной процедурой в одной среде, может не выглядеть предпочтительным в других. С другой стороны, сущность, которая как минимум стохастически (т.е., статистически чаще, чем нет, невзирая на степень зашумленности) не отвечает минимальным требованиям экономической рациональности, не может быть, кроме как случайно, названа как стремящейся к максимизации функции полезности. К таким сущностям теория игр не исходно не применяется.

Это не подразумевает, что теоретики непсихологических игр отвергают все принципиальные способы ограничения множеств РН подмножествами на основании относительной вероятности их возникновения. В частности, теоретики непсихологических игр склонны симпатизировать подходам, которые смещают акцент с рациональности на соображения, касающиеся информационной динамики игр. Возможно, мы не должны удивляться тому, что РН-анализ сам по себе часто мало может нам рассказать о прикладном, эмпирическом интересе в играх стратегической формы (напр., с рис. 6 выше), в которых информационная структура игры не отображается. Вопросы выбора равновесия намного более эффективно решаются для игр в развернутой форме.

Совершенствование подыгр

Для углубления нашего понимания игр с развернутой формой нам нужен пример с более интересной структурой, чем предлагает ДЗ.

Рассмотрим игру, описанную этим деревом:

Эта игра не призвана отражать какую-либо вымышленную ситуацию, это просто математический объект. (L и R здесь просто обозначают «левый» и «правый» соответственно.)

Теперь рассмотрим стратегическую форму этой игры:

Если вы не очень поняли, почему эта матрица выглядит так, вспомните, что стратегия должна указывать игроку, что делать на каждом информационном множестве, где у игрока есть ход. Поскольку в нашем примере каждый игрок выбирает из двух действий на информационном множестве (которых тоже два), то стратегий у каждого игрока всего четыре. Первая буква в обозначении стратегии сообщает игроку, что делать, когда он достигает первого информационного множества, вторая — когда достигнут второй. Т.е. LR для игрока II говорит ему играть L, если он оказывается перед множеством 5, и R, если он имеет дело со множеством 6.

Если вы рассмотрите изображенную на рисунке 10 матрицу, вы увидите, что среди РН есть (LL, RL). Это немного озадачивает, поскольку если игрок I достигнет своего второго информационного множества (7) в игре с развернутой формой, он вряд ли захочет сыграть там L; он выиграет больше, играя R в вершине 7. Один только поиск нэшевских равновесий не замечает этого, потому что РН нечувствительно к тому, что происходит вне [хода] розыгрыша (off the path of play). Игрок I, выбирая L на вершине 4, гарантирует, что вершина 7 не будет достигнута; собственно, это и значит оказаться «вне розыгрыша». Однако при анализе игр в развернутой форме нам следует интересоваться тем, что происходит вне розыгрыша, поскольку знание об этом оказывает решающее влияние на то, что происходит с самим розыгрышем.

Например, именно тот факт, что Игрок I сыграл бы R на вершине 7, вынуждает Игрока II играть L на вершине 6, и именно поэтому Игрок I не выберет R на вершине 4. Игнорируя результаты вне траектории розыгрыша, мы лишаем себя значимой для решений игры информации, как это делает простой поиск нэшевских равновесий. Обратите внимание на то, что повод сомневаться в том, что РН является полностью удовлетворительной концепцией равновесия само по себе, не имеет ничего общего с представлениями о рациональности, как в случае уточнения концепций, рассмотренных в разделе 2.5.

Теперь применим алгоритм Цермело к развернутой форме нашего примера. Начнем, опять же, с последней подыгры, начинающейся с вершины 7. Это ход игрока I, и он выберет R, потому что предпочитает выигрыш пяти очков выигрышу четырех, которые он получит, сыграв L. Поэтому мы назначаем выигрыш (5, -1) вершине 7. Таким образом, на вершине 6 игрок II должен выбирать между (-1, 0) и (5, -1). Он выбирает L. На вершине 5 игрок II выбирает R (0,5). На вершине 4 игрок I, таким образом, выбирает между (0, 5) и (-1, 0), и поэтому он играет L. Заметим, что, как и в игре заключенных, в терминальной вершине результатом является (4, 5) на вершине 7 — что по Парето предпочтительнее РН. Но, опять же, динамика игры препятствует достижению этого результата.

Тот факт, что алгоритм Цермело выбирает вектор (LR, RL) в качестве уникального решения игры, показывает, что он дает нечто иное, чем просто РН. Фактически, он генерирует идеальное равновесие подыгры (ИРП) для данной игры. Это дает результат, который обеспечивает достижение РН не только для всей игры, но также и для каждой подыгры. Это концепция решения убедительна, потому что, опять же в отличие от рафинирований из раздела 2.5, она не требует «дополнительной» рациональности от агентов, в том смысле что не ожидает, что они будут руководствоваться философскими представлениями о «том, что целесообразно». Однако она предполагает, что игроки не только знают все, что стратегически важно них в этой ситуации, но и используют всю эту информацию. В спорах об основах экономики это часто называют аспектом рациональности, как во фразе «рациональные ожидания». Но, как отмечалось ранее, следует соблюдать осторожность, дабы не спутать общую нормативную идею рациональности с вычислительной мощностью и обладанием запасом времени и энергии, позволяющим использовать ее наиболее полно.

Агент, разыгрывающий совершенную стратегию в подыгре, просто выбирает на каждой вершине путь, который приносит ему самый высокий выигрыш в подыгре, исходящей от этой вершины. ИРП предсказывает результат игры только в случае, если при решении игры игроки предвидят, что все они поступят таким образом.

Главная ценность поиска ИРП для игр расширенной формы в том, что он позволяет определить структурные ограничения социальной оптимизации. В нашем текущем примере игроку I было бы лучше, а игроку II не хуже, оказаться в левой вершине, исходящей из вершины 7, чем на результате ИРП. Однако экономическая рациональность игрока I и осведомленность игрока II об этом блокируют социально эффективный исход. Если наши игроки хотят здесь добиться более социально эффективного результата (4,5), они должны поменять свои установки, дабы изменить структуру игры.

Перестройка институциональных и информационных структур для повышения вероятности эффективных результатов в играх, в которые действительно играют агенты (то есть индивидуумы, корпорации, правительства и т.д.), называется дизайном механизмов и является одной из ведущих областей прикладного использования теории игр. Основные техники дизайна механизмов разбираются в книге Гурвича и Рейтера (Hurwicz and Reiter 2006), первый из которых за свою новаторскую работу в этой области получил Нобелевскую премию.

Интерпретация выигрышей: мораль и эффективность в играх

Многие читатели, но особенно философы, могут задуматься, почему для нашего последнего примера нужен дизайн механизмов, если игроки не являются патологическими социопатами. Разумеется, они могли бы просто увидеть, что результат (4,5) в социальном и моральном отношении превосходит все остальные; и поскольку здесь также принимается за само собой разумеющимся, что они могут проследить последовательность действий, которая приводит к этому эффективному результату, то какой же теоретик игр посмеет заявить, что этот результат недостижим без изменения игры?

Это возражение, что взывает к особой концепции рациональности, на которой настаивал Иммануил Кант, демонстрирует, что многие философы понимают под «рациональностью» нечто большее, чем теоретики игр. Эта тема активно и полемически исследуется Бинмором (Binmore 1994, 1998).

Вся эта сложная философская полемика относительно рациональности иногда порождает заблуждения ввиду неверного истолкования слова «полезность» в непсихологической теории игр.

Чтобы устранить эту ошибку, давайте вновь рассмотрим дилемму заключенного.

Мы видели, что в уникальном нэшевском равновесии ДЗ оба игрока получают меньшую полезность, чем они могли бы получить от сотрудничества. Это может сильно удивить вас, даже если вы не являетесь кантианцем (как это удивило многих комментаторов). Разумеется, можете подумать вы, что это просто итог сочетания эгоизма и паранойи игроков. Они, во-первых, не учитывают общественное благо, а после еще сильнее усугубляют свое положение, будучи слишком ненадежными для соблюдения соглашений.

Подобные соображения широко распространены и крайне запутаны. Чтобы лишить их влияния, давайте для начала введем некую терминологию для обсуждения результатов. Экономисты, изучающие благосостояние, обыкновенно измеряют общественное благо в терминах Парето-оптимальности, или оптимальности по Парето.

Распределение полезности β называется Парето-превосходящим по сравнению с распределением δ в случае, если из состояния δ возможно перераспределить полезность в β так, что по крайней мере один игрок выигрывает больше в β, чем в δ, и никто при этом не выигрывает меньше. Неспособность перейти от неоптимального по Парето к парето-оптимальному распределению неэффективна, поскольку сама возможность β показывает, что в δ некоторая доля полезности теряется впустую. Так вот, результат (3,3), который соответствует сотрудничеству в нашей модели ДЗ, явно превосходит по Парето взаимное предательство; на (3,3) обоим игрокам лучше, чем на (2,2). Поэтому верно, что ДЗ приводит к неэффективным результатам. Это справедливо и для нашего примера в разделе 2.6.

Однако неэффективность не должна ассоциироваться с безнравственностью. Функция полезности для игрока должна отражать все, что волнует игрока — а это может быть что угодно. Мы описали наших заключенных и их ситуацию так, будто они действительно заботятся только об относительной продолжительности сроков своего заключения, но это несущественно. Что делает игру примером ДЗ — так это ее структура выигрышей и только она. Фигурально выражаясь, «заключенными» игроками могут быть две матери Терезы, каждая из которых беспокоится не о себе, а о голодающих детях. Примем, что одна мать — собственно, Тереза — хочет накормить детей Калькутты, в то время как мать Хуанита хочет накормить детей Боготы. И предположим, что международный благотворительный фонд пожертвует максимальную сумму, если обе святых выберут один и тот же город; даст вторую по величине сумму, если они выберут города друг друга (т.е. Тереза — Боготу, а Хуанита — Калькутту) и самую низкую сумму, если каждая из них выберет свой собственный город. Наши святые здесь находятся в ситуации ДЗ, хотя они едва ли эгоистичны или не заботятся об общественном благе.

А теперь вернемся к нашим заключенным и предположим, что, вопреки нашим ожиданиям, они ценят благополучие друг друга так же, как и свое собственное. В этом случае это должно сказываться на их функциях полезности и, следовательно, на их выигрышах. Если их структуры платежей изменятся таким образом, что, например, им будет настолько плохо от своей причастности к неэффективности, что они предпочтут лишние годы заключения стыду, они больше не будут находиться в ДЗ. Но все это демонстрирует? То, что не всякая возможная ситуация — дилемма заключенного; это не показывает, что эгоизм входит в число предпосылок теории игр. Логика ситуации заключенных, а не психология удерживает их в капкане конечной неэффективности, и если они действительно оказались в нем, то из него нет иного выхода (если пренебречь дополнительными трудностями, которые будут обсуждаться ниже). Агентам, которые желают избегать неэффективных результатов, следует просто не допускать возникновения некоторых игр; сторонник кантовской рациональности на самом деле предлагает игрокам попытаться выйти из сложившейся игры, превратившись в агентов другого типа.

Короче, из этого следует, что игра частично определяется выигрышами, которые назначаются игрокам. В любой ситуации приписывания этих выигрышей должны опираться на достоверные эмпирические данные. Если предлагаемое решение подразумевает скрытое изменение выигрышей, то это «решение» на самом деле скрыто подменяет тему и отклоняется от стандартов моделирования.

«Дрожащая рука» и равновесие квантильных откликов (QRE)

Сказанное выше открывает путь к философскому затруднению, над которым работают те, кого все еще интересуют логические основания теории игр. Этот вопрос можно поставить по отношению к любому примеру, но мы обратимся к изящному примеру Кристины Биккьери (Bicchieri 1993). Рассмотрим следующую игру:

Равновесный по Нэшу итог один — он находится в крайней левой вершине, отходящей от вершины 8. Чтобы увидеть это, снова воспользуемся обратной индукцией. В вершине 10 игрок I сыграет L дабы получить 3, оставляя игроку II выигрыш в 1. Игрок II может добиться большего, сыграв L в вершине 9 и оставив I выигрыш в 0. Чтобы избежать этого, I сыграет L в вершине 8; это он и делает — так что игра заканчивается без передачи хода игроку II. Биккьери (наряду с другими авторами, включая Binmore 1987, Pettit and Sugden 1989) ставит следующую проблему. Игрок I играет L в вершине 8, потому что ему известно, что Игрок II экономически рационален, и потому в вершине 9 сыграет L, потому что Игрок II знает, что Игрок I экономически рационален и в вершине 10 сыграет L. Но теперь перед нами возникает следующий парадокс: Игрок I должен предполагать, что Игрок II в вершине 9 предскажет экономически рациональный ход Игрока I на вершине 10, несмотря на то, что он достиг вершины 9 — на которой он мог оказаться только в том случае, если Игрок I не является экономически рациональным! Если Игрок I не является экономически рациональным, Игрок II не может обосновать прогноз, что Игрок I не будет играть R в вершине 10, и в потому не очевидно, что Игрок II не должен играть R в вершине 9; и если Игрок II сыграет R в 9, то Игроку I гарантируется лучший выигрыш, если он сыграет L в вершине 8. Оба игрока используют обратную индукцию для решения игры; обратная индукция требует, чтобы Игрок I знал, что игрок II знает, что игрок I является экономически рациональным; но игрок II может решить игру только с помощью аргумента обратной индукции, который предполагает, что Игрок I ведет себя экономически рационально. Это парадокс обратной индукции.

Стандартный способ обойти этот парадокс, описанный в исследовательской литературе, — обратиться к идее «дрожащей руки», предложенной Зельтеном (Selten 1975). Она состоит в том, что решение и его последствия могут быть «разнесены» с некоторой ненулевой вероятностью, сколь бы малой она ни была. То есть игрок может желать предпринять некое действие, но затем ошибиться в розыгрыше и направить игру по другому пути. Если есть даже отдаленная возможность, что игрок может совершить ошибку, — его «рука может дрогнуть», — то игрок, используя аргумент от обратной индукции, не впадает в противоречие, предполагая, что другой игрок изберет путь, который экономически рациональный игрок выбрать не может. В нашем примере Игрок II мог размышлять о том, что делать в вершине 9, исходя из предположения, что Игрок I выбрал L в вершине 8, но затем пошел по другому пути.

Гинтис (Gintis 2009) указывает, что кажущийся парадокс возникает не только из-за нашего предположения об экономической рациональности обоих игроков. Он также опирается на предпосылку, что каждый игрок знает и руководствуется в своих размышлениях тем, что другой игрок экономически рационален. Из-за этой предпосылки догадки каждого игрока о том, что происходит вне пути к равновесию игры, становятся противоречивы. У игрока есть основания учитывать неравновесные возможности, если: а) он считает, что его противник экономически рационален, но его рука может дрогнуть; б) допускает ненулевую вероятность того, что противник не является экономически рациональным; в) сомневается в том, что он верно понимает функцию полезности противника.

Как подчеркивает Гинтис, в общем виде эта проблема при решении игр в развернутой форме по алгоритму Цермело для игр с ИРП такова: у игрока нет причин разыгрывать даже равновесную по Нэшу стратегию, если он не ожидает от других игроков, что они также будут придерживаться нэшевской стратегии. Мы вернемся к этому вопросу ниже, в разделе 7.

Парадокс обратной индукции, подобно затруднениям, связанным с рафинированием равновесия, проблематичен главным образом для тех, кто рассматривает теорию игр как часть нормативной теории рациональности (а именно, как часть более широкой теории стратегической рациональности).

Мнения специалистов в области непсихологической теории игр об «иррациональном» поведении и осторожности, которую она провоцирует, могут разниться.

Некоторые указывают на эмпирический факт, что реальные агенты, в том числе люди, должны осваивать равновесные стратегии игр, в которые они играют, по крайней мере, когда игры хоть сколько-нибудь сложны. Исследования показывают, что даже столь простые игры, как дилемма заключенного, требуют обучения (Ledyard 1995, Sally 1995, Camerer 2003).

Сказать, что люди должны изучать равновесные стратегии, значит сказать, что нам следует быть несколько более искушенными, чем было указано ранее, в построении функций полезности из поведения при применении теории выявленных предпочтений (RPT).

Вместо построения функции полезности на основе отдельных эпизодов, нам следует делать это на основе наблюдений за регулярными паттернами стабилизировавшегося поведения, т.е. после того, как субъекты уже изучили игру.

И вновь, дилемма заключенного здесь будет нам хорошим примером. В повседневной жизни люди редко сталкиваются с однократными ДЗ, им куда чаще приходится иметь дело с повторяющимися дилеммами, участники которых не случайные друг другу люди. В результате, когда экспериментаторы заставляют их играть однократную ДЗ, испытуемые обычно начинают играть так, как если бы эта игра была одним раундом повторяющейся ДЗ. Повторяющаяся ДЗ имеет множество равновесий Нэша, которые предполагают сотрудничество, а не отступничество.

Таким образом, экспериментальные субъекты, как правило, вначале сотрудничают, но после нескольких раундов научаются предавать. Экспериментатор не может сделать вывод, что он успешно воспроизводит однократную ДЗ в своем эксперименте, пока не убедится в стабилизации такого поведения.

Если игроки понимают, что другим игрокам нужно сначала разобраться в структуре игры и ее равновесиях опытным путем, это дает им основание учитывать также и то, что происходит вне равновесных путей решения игры в развернутой форме. Конечно, если игрок опасается, что другие игроки не изучили равновесие, это вполне может лишить его стимула разыгрывать стратегию равновесия.

Это порождает множество серьезных проблем социального обучения (Fudenberg and Levine 1998). Как несведущим игрокам научиться разыгрывать равновесие, если искушенные игроки им это не показывают, поскольку у искушенных игроков нет мотивации играть в стратегии равновесия, пока неискушенные этому не научились? Ключевой ответ для прикладного применения теории игр к взаимодействию между людьми гласит: молодежь социализируется, пока растет в институциональных сетях, у которых есть культурные нормы. Большинство сложных игр, в которые играют люди, разыгрывают те, кто уже был социализирован, то есть освоил игровые структуры и равновесия (Ross 2008a). Новички вынуждены в этом случае лишь копировать тех, чья игра кажется ожидаемой и понятной для остальных. Институты и нормы насыщены напоминаниями, типа нравоучений и легко запоминающихся «правил большого пальца», которые помогают людям помнить о том, чем они вообще занимаются (Clark 1997).

Как отмечалось в разделе 2.7, если наблюдаемое поведение не стабилизируется вокруг равновесных состояний игры, и нет никаких свидетельств тому, что обучение все еще продолжается, аналитику следует сделать вывод, что он неправильно смоделировал изучаемую им ситуацию. Вероятно, он либо неправильно задал функции полезности игроков, либо доступные игрокам стратегии, либо доступную для них информацию. Учитывая сложность многих изучаемых социологами ситуаций, не следует удивляться тому, что модели часто оказываются неправильными. Теоретики, занимающиеся прикладными играми, должны тратить много сил на обучения, точно так же, как и их испытуемые.

Таким образом, парадокс обратной индукции — лишь видимость. Если игроки не имеют опыта равновесной игры друг с другом в прошлом, даже если они экономически рациональны и уверены в рациональности партнера, мы должны понимать, что они допускают, что другие игроки могут не вполне понимать структуры игры. Это объясняет, почему люди, даже если они являются экономически рациональными агентами, могут зачастую — или даже обыкновенно — играть так, будто они верят в «дрогнувшую руку».

Изучение равновесий может принимать различные формы для разных агентов, а также для игр различного уровня сложности и риска. Включение этого фактора в теоретико-игровые модели взаимодействий, соответственно, открывает перед нами огромное множество новых технических решений. Наиболее развитая общая теория изложена Фуденбергом и Левиным (Fudenberg and Levine 1998).

Выше мы уже упоминали, что люди обыкновенно играют так, будто они верят в «дрожание рук». Причина этого заключается в том, что при взаимодействии людей мир не дает им подсказок, которые бы поясняли им структуру игры, в которую они играют. Они вынуждены строить и проверять гипотезы относительно структуры игры, опираясь на социальный контекст. Иногда контекст задают институциональные правила. Например, когда человек входит в магазин и видит ценник на что-то, что он хотел бы иметь, он знает, не нуждаясь в догадках или обучении чему-либо, что он участвует в простой игре «либо да, либо нет». А оказавшись на рынке, например, он может знать, что может торговаться, и также знает правила для этого.

Учитывая сложные взаимоотношения между теорией обучения и теорией игр (все еще нерешенные), приведенное выше рассуждение может привести к мысли, что теория игр никогда не сможет быть применена к ситуациям с участием новичков. К счастью, это, однако, не так. Маккелви и Палфри в двух своих весьма влиятельных работах середины-конца 1990-х (McKelvey and Palfrey 1995, 1998) разработали концепцию решения равновесия дискретного отклика (QRE), или просто дискретного равновесия. QRE не является рафинированием нэшевского равновесия, в том смысле, что оно не является философски мотивированной попыткой усилить РН с опорой на нормативные стандарты рациональности. Это, скорее, метод расчета равновесных свойств выборов, сделанных игроками, предположения которых о возможных ошибках в выборе других игроков не определены. Таким образом, QRE является стандартным средством в инструментарии экономистов-экспериментаторов, которые пытаются оценить распределение функций полезности в популяциях реальных людей, помещенных в модельные игровые ситуации. Таким образом, QRE нельзя было бы применить на практике до разработки эконометрических пакетов, таких как Stata, позволяющих вычислять QRE по адекватным информативным записям наблюдений за сложными играми. QRE редко используется поведенческими экономистами и почти никогда не используется психологами при анализе лабораторных данных. Вследствие этого многие исследователи из этой группы делают крайне драматичные риторические заявления, «открывая», что реальные люди в экспериментальных играх часто не сходятся на РН. Но хотя РН и представляет собой в некотором смысле минималистскую концепцию решения, поскольку достаточно сильно абстрагируется от информационной структуры, в своей категорической форме одновременно является сильным эмпирическим ожиданием (то есть если ожидается, что игроки будут играть так, как если бы они были уверены, что все остальные игроки также сыграют стратегии РН). Прогнозирование розыгрыша, соответствующего QRE, согласуется — а, точнее, мотивировано — с точкой зрения, согласно которой РН воплощает центральную идею стратегического равновесия. С философской точки зрения отношение между РН и QRE можно описать следующим образом. РН определяет логический принцип, который хорошо подходит для «настройки» нашего мышления и разработки типовых стратегий для моделирования новых классов социальных явлений. Для оценки же реальных эмпирических данных необходимо иметь возможность определить равновесие статистически. QRE представляет собой способ сделать это сообразно логике РН. Эта идея настолько масштабна, что в теории игр она все еще остается малоисследованной. Современные способы истолкования QRE представлены в работе Гори, Холта и Палфри (Goeree, Holt and Palfrey 2016).

Неопределенность, риск и секвенциальное равновесие

Во всех играх, которые мы моделировали до этого момента, участвовали игроки, выбиравшие из чистых стратегий, в которых каждый искал на каждой вершине один оптимальный курс действий, представляющий собой наилучшую реакцию на действия других.

Однако часто полезность для игрока оптимизируется при помощи смешанной стратегии, которая выглядит как выбор одного из возможных действий посредством подбрасывания «нечестной» монетки. (Позже мы увидим, что существует альтернативная интерпретация смешивания, не предполагающая рандомизации в определенном информационном множестве, но мы начнем здесь с интерпретации подбрасывания монетки, а затем продолжим в части 3.1).

Если ни одна чистая стратегия не максимизирует полезность игрока по отношению ко всем стратегиям противника, используется смешивание. Примером подобного является игра с преодолением реки, описанная в разделе 1. Как мы видели, задача в этой игре состоит в том, что если в ходе размышления беглец выбирает некоторый мост в качестве оптимального, то следует допустить, что его преследователь сможет воспроизвести тот же самый ход мысли. Беглец может уйти от погони только в том случае, если охотник не может однозначно предсказать, по какому мосту будет переправляться беглец. Симметрия логического рассуждения упирается в то, что беглец сможет удивить преследователя только в том случае, если он окажется способен удивить себя.

Давайте забудем на мгновение про камнепады и кобр и представим, что все мосты безопасны в равной степени. Предположим также, что беглец не имеет особых сведений о своем преследователе, которые позволили ему отважиться на то, чтобы построить специфическое распределение вероятностей для доступных стратегий преследователя. В этом случае лучшим вариантом для беглеца будет бросок трехгранной кости, в которой каждая сторона представляет один из мостов (или шестигранного кубика, на котором каждый мост представлен двумя гранями). Он также должен предварительно взять на себя обязательство использовать мост, выбранный с помощью данного средства рандомизации. Это закрепляет шансы его выживания независимо от того, как поступит преследователь; но поскольку у преследователя нет оснований предпочесть какую-либо доступную ему — чистую или смешанную — стратегию, и поскольку мы в любом случае предполагаем, что его эпистемическая ситуация симметрична ситуации беглеца, мы можем предположить, что преследователь также сделает свой выбор на основании броска трехгранной кости. Теперь вероятность успеха для беглеца составляет 2/3, а вероятность преследователя поймать его — 1/3. Ни беглец, ни преследователь не могут улучшить свои шансы, учтя рандомизирующее смешение другого, поэтому две стратегии рандомизации находятся в равновесии Нэша. Обратите внимание на то, что если один игрок рандомизирует, то другой преуспеет одинаково при любом смешении вероятностей для мостов, поэтому комбинаций наилучших ответов бесконечно много. Тем не менее каждый игрок вынужден беспокоиться о том, что любая неслучайная стратегия будет увязана с некоторым фактором, который другой игрок может обнаружить и использовать. Поскольку любую неслучайную стратегию можно таким образом обыграть при помощи другой неслучайной стратегии, то в игре с нулевой суммой, к каковой относится наш пример, равновесным по Нэшу будет только вектор рандомизированных стратегий.

Теперь повторно введем параметрические факторы, т.е. падающие камни на мосту №2 и кобр на мосту №3. Опять же, предположим, что беглец точно переправится по мосту №1 успешно, сделает это 90-процентным шансом на успех по мосту №2 и 80-процентным — по мосту №3. Мы можем решить эту игру, если сделаем определенные предположения о функциях полезности двух игроков. Предположим, что игрок 1, беглец, заботится только о жизни или смерти (предпочитая жизнь смерти), в то время как преследователь просто хочет доложить, что беглец мертв, и предпочитает это докладу о том, что беглец ушел. (Иными словами, ни один из игроков не заботится о том, как именно выживет или погибнет беглец). Предположим также, что ни один из игроков не получает ни пользы, ни вреда от того, что решается рисковать. В этом случае беглец просто берет свою первоначальную формулу рандомизации и взвешивает ее в соответствии с различными уровнями параметрической опасности на трех мостах. Каждый мост следует рассматривать как лотерею возможных результатов беглеца, в которых каждая лотерея имеет иную ожидаемую выгоду с точки зрения позиций в своей функции полезности.

Рассмотрим ситуацию с точки зрения преследователя. Выбирая сочетание вероятностей для мостов, он будет использовать свою равновесную по Нэшу стратегию, так что беглецу при выборе между чистыми стратегиями позиция оппонента безразлична. Мост с камнепадами для него в 1,1 раза опаснее, чем безопасный мост. Поэтому он будет безразличным к выбору между ними, если вероятность встретить на безопасном мосту охотника будет в 1,1 раза выше, чем на мосту под осыпающейся скалой. Мост с кобрами в 1,2 раза опаснее для беглеца, чем безопасный мост. Поэтому он будет безразличен к выбору между этими мостами, если вероятность встретить преследователя на безопасном мосту в 1,2 раза выше, чем на мосту с кобрами. Предположим, мы используем параметрическую выживаемость беглеца на каждом мосту s1, s2 и s3. Преследователь снижает чистую выживаемость беглеца для любой пары мостов тем, что может ожидать его на каждом из них — это выражается через p1 и p2, так, что

s1 (1 − p1) = s2 (1 − p2)

Поскольку p1 + p2 = 1, мы можем переписать это так:

s1 × p2 = s2 × p1

так что

p1/s1 = p2/s2.

Таким образом, преследователь находит свою равновесную по Нэшу стратегию, решая следующую систему одновременных уравнений:

1 (1 − p1) = 0,9 (1 − p2)

                = 0,8 (1 − p3)

p1 + p2 + p3 = 1.

Тогда

p1 = 49/121

p2 = 41/121

p3 = 31/121

Теперь введем f1, f2, f3 для обозначения вероятностей, с которыми беглец выбирает каждый соответствующий мост. Тогда беглец находит свою стратегию РН, решая

s1 × f1 = s2 × f2

           = s3 × f3

так что

1 × f1 = 0.9 × f2

          = 0.8 × f3

одновременно с

f1 + f2 + f3 = 1.

Тогда

f1 = 36/121

f2 = 40/121

f3 = 45/121

Эти два набора РН-вероятностей сообщают каждому игроку, как задать вес игрального кубика перед броском. Обратите внимание — возможно, к своему удивлению, — что беглец, хотя и не получает по условиям нашей игры удовольствия от азартных игр, выбирает более рискованные мосты с большей вероятностью. Это единственный способ сделать преследователя безразличным к тому, на какой мост ему делать ставку, что, в свою очередь, максимизирует вероятность счастливого исхода для беглеца.

Мы смогли решить эту игру напрямую, потому что мы задаем функции полезности так, чтобы сделать ее игрой с нулевой суммой или строго конкурентной. Это значит, что любой прирост ожидаемой полезности для одного игрока представляет собой точно симметричную потерю для другого. Однако часто это условие может не выполняться. Предположим теперь, что функции полезности более сложны. Преследователь больше всего предпочитает результат, при котором он пристрелит беглеца, тому, где беглец погибнет самостоятельно — под камнепадом или от укуса кобры; а самостоятельную смерть беглеца он предпочитает удачному побегу. Беглец же предпочитает быструю смерть от выстрела долгим мукам под камнепадом или ужасу встречи с коброй. А больше всего, конечно, он предпочитает спастись. Предположим, что беглец намного больше заботится о своем выживании, чем тем, каким именно способом ему погибнуть. Мы не можем решить эту игру, как и прежде, только с опорой на порядковые функции полезности игроков, поскольку интенсивность их относительных предпочтений теперь будет соответствовать их стратегиям.

До 1947 года (работы фон Неймана и Моргенштерна) подобные ситуации по своей сути были непонятны аналитикам, потому что полезность не отражает такую скрытую психологическую переменную, как удовольствие.

Как мы уже говорили в разделе 2.1, полезность является лишь мерой относительных поведенческих склонностей, с учетом когда нам точно известны отношения между предпочтениями и выборами. Поэтому нет смысла сравнивать кардинальные — т.е. чувствительные к интенсивности — предпочтения наших игроков, поскольку не существует независимой, для всех одинаковой линейки, которую бы мы могли использовать. Как же тогда моделировать игры, в которых важна кардинальная информация?

В конце концов, для моделирования игр требуется, чтобы все полезности для игроков учитывались одновременно.

Важнейшей результатом работы фон Неймана и Моргенштерна было решение этой проблемы. Здесь мы кратко изложим предложенную ими оригинальную технику получения кардинальных функций полезности из порядковых. Следует подчеркнуть, что изложенное ниже является лишь наброском, необходимым для того, чтобы демистифицировать кардинальную полезность для вас как для того, кто заинтересован в философских основаниях теории игр и круге проблем, к которым она может быть применена. Составление руководства, по которому вы могли бы строить кардинальные функций самостоятельно, потребовало бы многих страниц. Такие руководства доступны во многих учебниках.

Предположим, что мы теперь назначаем следующую порядковую функцию полезности беглецу, пересекающему реку:

Спасение ≫ 4

Смерть от выстрела ≫ 3

Смерть от камнепада ≫ 2

Смерть от укуса змеи ≫ 1

Мы полагаем, что он предпочитает свободу смерти в большей степени, чем любую из форм смерти другой. Это должно отражаться на том, какое поведение он предпочтет, следующим образом. В игре с переправой его готовность рискнуть, дабы усилить относительную вероятность побега по сравнению с вероятностью быть застреленным, будет выше, чем в ситуации, когда он оценивает риски попытки усилить относительную вероятность быть застреленным по сравнению с вероятностью умереть от змеиного укуса. Эта логика — важнейший элемент решения проблемы кардинализации, предложенного фон Нейманом и Моргенштерном.

Предположим, что мы попросили беглеца выбрать из доступного набора результатов лучший и худший. «Лучший» и «худший» определяются при помощи ожидаемых выигрышей, как показано на примере нашей игры с нулевой суммой: игрок максимизирует свой ожидаемый выигрыш, если при выборе лотерей, содержащих только два возможных приза, его выбор всегда устремлён к максимизации вероятности наилучшего результата — назовем его W — и минимизации вероятности наихудшего — назовем его L.

Теперь расширим множество возможных призов, чтобы оно включало призы, которые агент оценивает как промежуточные между W и L.

Мы обнаруживаем, что для набора результатов, содержащих такие призы, имеется такая лотерея, что наш агент не видит отличий между ней и лотереей, включающей только W и L.

В нашем примере это лотерея, включающая в себя смерть от пули и смерть от камня. Назовем эту лотерею T. Мы определим q = u(T) как функцию полезности от результатов на ряд действительных чисел (в отличие от порядкового), так что если q — ожидаемый выигрыш в T, то агенты не видят различий между выигрышем T и выигрышем лотереи T*, в которой W встречается с вероятностью u(T), а L встречается с вероятностью 1–u(T).

Если поведение агентов соблюдает принцип сокращения сложных лотерей (reduction of compound lotteries, ROCL) — т.е. не получает или не теряет в полезности от рассмотрения более сложных лотерей, — то набор отображений результатов в T в uT* дает функцию полезности фон Неймана-Моргенштерна (vNMuf) с кардинальной структурой по всем результатам в T.

Что именно мы здесь сделали? Мы предоставили нашему агенту выбор из лотерей, вместо того чтобы дать ему выбирать результаты, и увидели, какому именно дополнительному риску смерти он готов подвергнуться, чтобы изменить свои шансы на одну смерть по отношению к другой. Отметим, что это кардинализирует структуру предпочтений агента только по отношению к специфичным для этого агента точкам сравнения W и L; процедура никак не сравнивает экстра-порядковые предпочтения между агентами, что позволяет ясно показать, что построение функции vNMuf не вводит никакого потенциально объективного психологическего элемента. Более того, два агента в рамках одной игры или один агент в различных обстоятельствах могут по-разному относиться к риску. Возможно, в игре с переправой преследователь, чья жизнь не поставлена на карту, будет азартен, в то время как беглец осторожен. Однако при анализе этой игры мы не должны сравнивать кардинальную полезность для преследователя с кардинальной полезностью для беглеца. Оба агента, в конце концов, могут достичь своих равновесных по Нэшу стратегий, если смогут оценить вероятности, которые каждая сторона присваивает действиям другой. Это значит, что каждый агент должен знать обе функции vNMuf; но ни один из них не нуждается в том, чтобы сравнить ценность результатов, из которых они выбирают.

Теперь мы можем заполнить остальную часть матрицы для игры с переправой, которую мы нарисовали в разделе 2. Если оба игрока не питают страсти к риску и их выявленные предпочтения учитывают ROCL, то у нас имеется достаточно информации, чтобы распределить ожидаемую полезность, выражая ее путем умножения исходных выигрышей на соответствующие вероятности, как результаты в матрице. Предположим, что охотник ждет на мосту со кобрами с вероятностью x, а на скалистом мосту с вероятностью y. Поскольку сумма его вероятностей для трех мостов должна быть равна 1, это означает, что он должен ждать на безопасном мосту с вероятностью 1 — (x + y). Назначая выигрыш беглецу за смерть 0, и 1, если он уйдет от погони, а выигрыши преследователя противоположным образом, получаем полную матрицу следующего вида:

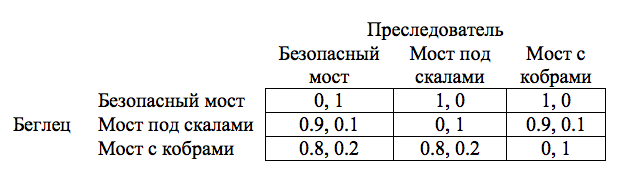
Теперь мы можем непосредственно по матрице узнать об игре следующие факты: ни одна пара чистых стратегий не является парой лучших ответов друг на друга. Таким образом, единственное РН в игре требует, чтобы по меньшей мере один игрок использовал смешанную стратегию.

Убеждения и субъективные вероятности

Во всех наших примерах до этого момента мы предполагали, что убеждения игроков относительно вероятностей в лотереях соответствуют объективным вероятностям. Но в реальных ситуациях интерактивного выбора агенты часто вынуждены полагаться на свои субъективные оценки или восприятие вероятностей. Автор одной из величайших работа по поведенческим и социальным наукам XX века Леонард Сэвидж показал (Savage 1954), как можно включить субъективные вероятности и их отношения к предпочтениям в теорию ожидаемой полезности фон Неймана-Моргенштерна. Действительно, с достижением Сэвиджа теория ожидаемой полезности (EUT) была, наконец, полностью формализована. Затем, чуть более десятилетия спустя, Джон Харсаньи (Harsanyi 1967) показал, как решать игры с использованием максимизаторов ожидаемой полезности Сэвиджа. Принято считать, что с этого момента теория игр наконец созрела для того, чтобы стать прикладным инструментом поведенческих и социальных наук, и была признана как таковая, когда Харсаньи вместе с Нэшем и Зельтеном в 1994 году стали первыми теоретиками игр, получившими Нобелевскую премию.

Как мы уже видели, — рассматривая необходимость того, чтобы играющие в игры люди освоили равновесие «дрожащей руки» и QRE, — при моделировании стратегических взаимодействий людей, мы должны допускать тот факт, что люди, как правило, не уверены в том, что их модели других игроков верны. Эта неуверенность проявляется в том, как они выбирают стратегии. Более того, некоторые действия могут быть предприняты специально лишь для того, чтобы проверить точность предположений игрока относительно других игроков. Расширенная Харсаньи теория игр включает в себя эти важнейшие элементы.

Рассмотрим игру с неполной информацией на трех игроков, известную как «лошадь Зельтена» (получившую такое имя в честь ее изобретателя Рейнхарда Зельтена, нобелевского лауреата по экономике, — и из-за формы ее дерева; взято из Kreps 1990: 426):

У этой игры есть четыре равновесия по Нэшу: (L, l2, l3), (L, r2, l3), (R, r2, l3) и (R, r2, r3). Рассмотрим четвертое. Оно возникает, когда игрок I играет R, а игрок II играет r2; все информационное множество игрока III оказывается вне пути игры, и для результата действия игрока III не имеют значения. Однако игрок I не играл бы R, если бы игрок III видел разницу между позицией в вершине 13 и позицией в вершине 14. Структура игры благоприятствует усилиям игрока I предоставить игроку III информацию, которая вскрыла бы его закрытое информационное множество. Игроку III следует поверить этим данным, поскольку структура игры показывает, что у Игрока I есть стимул говорить правду. Тогда решением игры будет ИРП для игры с (теперь) совершенной информацией: (L, r2, l3).

Теоретики, рассматривающие теорию игр как часть нормативной теории общей рациональности, например, большинство философов, а также сторонники программы уточнения понятия равновесия среди экономистов, разработали стратегию, которая бы определяла это решение на общих принципах. Обратите внимание: игрок III в «лошади Зельтена» может задуматься, выбирая стратегию: «Если я получил ход, была ли вершина моего действия достигнута из вершины 11 или вершины 12?» Иными словами, каковы условные вероятности того, что Игрок III находится в вершине 13 или 14, учитывая, что ход перешел к нему? Теперь, если Игрок III размышляет об условных вероятностях, тогда игрок I и игрок II, выбирая свои стратегии, думают об убеждениях Игрока III относительно этих условных вероятностей. В этом случае Игрок I должен строить догадки об убеждениях Игрока II по поводу убеждений Игрока III и убеждениях Игрока III по поводу убеждений игрока II, и т.д. Эти убеждения здесь не просто, как прежде, стратегические, поскольку они касаются не только того, что будут делать игроки при данных наборах выигрышей и в таких игровых структурах, но и о том, какого понимания условной вероятности они должны ожидать от других игроков.

Каких убеждений относительно условной вероятности игрокам разумно ожидать друг от друга? Если бы мы последовали за Сэвиджем (Savage 1954), мы бы предположили в качестве нормативного принципа, что они должны рассуждать сами и ожидать от других рассуждений в соответствии с правилом Байеса. Это подскажет им, как вычислить вероятность события F при информации E (обозначается «pr (F / E)»):

pr(F/E) = [pr(E/F) × pr(F)] / pr(E)

Если предположить, что убеждения игроков всегда согласуются с этим равенством, то мы можем определить последовательное равновесие (sequential equilibrium). Оно состоит из двух частей: (1) профиля стратегии § для каждого игрока, как и раньше, и (2) системы убеждений μ для каждого игрока. μ присваивает каждому информационному множеству h распределение вероятностей по вершинам в h с интерпретацией, что это убеждения игрока i(h) о том, где в его информационном множестве он находится, при условии, что информационное множество h достигнуто. Тогда последовательное равновесие является совокупностью профиля стратегий § и системы убеждений μ, согласующейся с правилом Байеса таким образом, что, начиная с любого информационного множества h на дереве, игрок i(h) играет в дальнейшем оптимально, учитывая, что, по его мнению, то, что происходило ранее, дано в μ(h), а то, что будет происходить при последующих ходах, дано посредством §.

Применим эту концепцию решения к игре «лошадь Зельтена». Вновь рассмотрим РН (R, r2, r3). Предположим, что игрок III назначает pr(1) своему убеждению в том, что если он получит ход, то он находится в вершине 13. Тогда игрок I, учитывая непротиворечивое μ(I), должен полагать, что игрок III будет играть l3, и в этом случае его единственная стратегия ПР — это L. Поэтому, хотя (R, r2, l3) и является РН, это не ПР.

Использование требования непротиворечивости в этом примере несколько тривиально, поэтому рассмотрим теперь второй случай (также взятый из Kreps 1990: 429):

Предположим, что игрок I играет L, игрок II играет l2, а игрок III играет l3. Предположим также, что μ(II) присваивает pr(0,3) вершине 16. В этом случае l2 не является стратегией ПР для игрока II, так как l2 приносит ожидаемый выигрыш 0,3(4) + 0,7(2) = 2,6, а r2 — ожидаемый выигрыш 3,1. Обратите внимание, что если мы повозимся со стратегическим профилем игрока III, оставив все остальное неизменным, l2 может стать стратегией ПР для игрока II. Если §(III) приводит к розыгрышу l3 с pr(0,5) и r3 с pr(0,5), то если игрок II сыграет r2, его ожидаемый выигрыш будет уже 2,2, поэтому (Ll2l3) будет последовательным равновесием. Теперь представим, что мы откатили μ(III) обратно, но изменили μ(II) так, чтобы игрок II считал, что условная вероятность находиться в вершине 16 больше 0,5; в этом случае l2 вновь не является стратегией ПР.

Идея последовательного равновесия, как мы надеемся, теперь ясна. Мы можем применить его к игре с переправой таким образом, чтобы преследователю не пришлось подбрасывать какие-либо монетки, для чего мы немного модифицируем игру. Предположим теперь, что охотник может дважды поменять мост, пока беглец переправляется, и поймает его, если встретится с ним на выходе с моста. Тогда стратегия ПР для преследователя заключается в том, чтобы разделить время своего пребывания на трех мостах в соответствии с пропорцией, заданной выше уравнением в третьем абзаце раздела 3.

Следует отметить, что, поскольку правило Байеса нельзя применить к событиям с вероятностью 0, его применение к ПР требует, чтобы игроки назначали ненулевые вероятности всем действиям, доступным в развернутой форме. Это требование закрепляется предположением, что все профили стратегии строго смешаны, т.е. что каждое действие в каждом информационном множестве имеет положительную вероятность. Мы увидим, что это просто эквивалентно предположению, что все руки иногда дрожат, или же что никакое ожидание не может быть определенным в достаточной мере. Говорят, что ПР является совершенной дрогнувшей рукой (trembling-hand perfect), если все равновесные стратегии являются наилучшими ответами на строго смешанные стратегии. Мы также не должны удивляться тому, что ни одна слабо доминируемая стратегия не может быть совершенной дрогнувшей рукой, поскольку вероятность дрогнувшей руки является для игроков наиболее убедительной причиной для того, чтобы избегать подобных стратегий.

Как может специалист в области теории непсихологических игр понять концепцию РН, которая является равновесием как действий, так и убеждений? Десятилетия экспериментов показали, что когда люди играют в игры, особенно в те, что в идеале требуют применения правила Байеса при выдвижении предположений об убеждениях других игроков, мы должны ожидать, что стратегические ответы будут в значительной степени гетерогенны. Множество видов информационных каналов обычно связывают разных агентов со структурами стимулов в их среде. Некоторые агенты действительно способны вычислять равновесия с той или иной погрешностью. Другие агенты в результате более или менее упрощенного условного обучения могут удовлетвориться диапазонами ошибок, стохастически дрейфующими вокруг равновесных значений. Третьи могут выбирать шаблонные ответы, копируя поведение других агентов или следуя эмпирическим правилам, встроенным в культурные и институциональные структуры и репрезентирующими коллективную историческую память.

Следует обратить внимание на то, что это весьма специфичная для теории игр проблема, а не простая реитерация более общего тезиса, верного для любой науки о поведении и гласящего, что с точки зрения идеальной теории поведение людей зашумлено.

В данной игре рациональность разыгрывания РН для агента — даже натренированного, осознающего свое положение, обеспеченного вычислительными ресурсами — будет зависит от частоты, с которой, как он ожидает, другие будут поступать аналогичным образом. Ожидая, что другие игроки отклонятся от равновесной по Нэшу игры, он может и сам в итоге отклонится от этой стратегии.

Вместо того, чтобы предсказывать, что игроки будут сами раскрывать строгие стратегии РН, опытный экспериментатор или специалист по моделированию будет ожидать, что между розыгрышем и ожидаемыми затратами на отклонение от РН будет какая-то связь.

Следовательно, оценка наиболее вероятного развития наблюдаемых действий, как правило, указывает на дискретное равновесие как на наилучший вариант по сравнению с любым РН.

Не надо думать, что аналитик, рассматривающий эмпирические данные таким образом, занимается «проверкой гипотезы» о том, что анализируемые агенты «рациональны». Скорее, он предполагает, что они являются агентами, то есть что существует систематическая взаимосвязь между статистическими изменениями паттернов их поведения и некоторыми взвешенными по риску кардинальными рейтингами возможных итоговых состояний. Если агенты являются людьми или институционально структурированными группами людей, которые наблюдают друг за другом и у которых есть стимулы пытаться действовать коллективно, критики будут считать эти гипотезы разумными, или даже прагматически не подлежащими сомнению — даже если они всегда могут быть отброшены с оглядкой на ненулевую вероятность каких-либо внезапных и необычных обстоятельств вроде тех, что иногда рассматривают философы (например, люди окажутся заранее запрограммированными неразумными механическими симулякрами, которые будут раскрыты, только если обстоятельства вызовут в них реакцию, которая не была заложена в их программу). Аналитик будет предполагать, что агенты будут реагировать на стимульные изменения в соответствии с теорией ожидаемой полезности Сэвиджа, особенно если агенты являются фирмами, изучившими ответные действия в условиях нормативно взыскательных условий рыночной конкуренции со многими игроками. Если субъекты аналитика являются отдельными людьми и, в особенности, если они находятся в нестандартной ситуации (относительно их культурного и институционального опыта), аналитик тогда допустит максимально правдоподобную модель, которая допускает, что спектр различных структур обеспечения полезности управляет различными подмножествами его данных. Все это говорится для того, чтобы подчеркнуть: применение теории игр не заставляет ученого эмпирически применять модель, которая, по всей вероятности, будет слишком точной и узкой по своей спецификации, чтобы правдоподобно соответствовать сложным хитросплетениям реального стратегического взаимодействия. Хороший специалист по прикладной теории игр также должен быть хорошо подготовленным эконометристом.

Повторяющиеся игры и координация

До сих пор мы ограничивались лишь однократными играми, то есть играми, в которых стратегические интересы игроков распространяются не далее, чем терминальные вершины их однократного взаимодействия. Однако игры часто проходят с учетом будущих игр, и это может значительно влиять на их результаты и равновесные стратегии. В этом разделе мы будем рассматривать повторяющиеся игры, то есть игры, в которых множества игроков предполагают встретить друг с друга в схожих ситуациях несколько раз. Вначале рассмотрим этот класс игр в ограниченном контексте многократно повторяющихся дилемм заключенного.

Мы видели, что в однократной ДЗ единственным нэшевским равновесием является взаимное отступничество. Однако это может больше не выполняться, если игроки ожидают встречи друг с другом в следующей ДЗ. Представим себе, что четыре фирмы, изготавливающие какие-то штуковины, договариваются поддерживать высокие цены путем совместного ограничения поставок. (То есть формируют картель). Это будет работать только в том случае, если каждая фирма будет сохранять согласованную квоту на производство. Обычно в таких ситуациях верно то, что каждая фирма может максимизировать свою прибыль, если она отклонится от квоты, в то время как другие продолжат соблюдать свои, так как она продаст больше штуковин по завышенной цене, созданной пока еще действующим картелем. В однократном примере все фирмы разделяют этот стимул на отступничество, потому картель незамедлительно распался бы. Однако фирмы в действительности ожидают, что они будут конкурировать друг с другом в течение длительного времени. Потому каждая фирма знает, что если она нарушит картельное соглашение, другие могут наказать ее путем достаточно долгого демпинга для того, чтобы погасить полученную ей краткосрочную выгоду. Разумеется, карающие фирмы будут также понесут убытки в период снижения цен. Но эти потери могут окупиться, если они восстановят картель, который обеспечит максимальные цены на длительный срок.

Одна простая и известная (но, вопреки широко распространенному мифу, необязательно оптимальная) стратегия сохранения кооперации в повторяющихся ДЗ называется «зуб за зуб». Эта стратегия гласит, что каждый игрок должен вести себя следующим образом:

i.      Всегда сотрудничать в первом раунде.

ii.     Далее действовать также, как и ваш противник в предыдущем раунде.

Если все члены группы будут играть по принципу «зуб за зуб», они никогда не столкнутся с отступничеством.

Поэтому в популяции, где все остальные разыгрывают стратегию «зуб за зуб», «зуб за зуб» является рациональным ответом для каждого игрока; всеобщий розыгрыш «зуб за зуб» есть нэшевское равновесие. Вы можете часто слышать от людей, которые знают немного (но недостаточно) о теории игр, что на этом история заканчивается. Однако это не так.

Есть две сложности.

Во-первых, игроки не должны быть знать о том, когда именно закончится их взаимодействие. Предположим, игроки знают, какой раунд будет последним. В этом раунде можно будет максимизировать полезность отступничеством, они не понесут наказание. Теперь рассмотрим предпоследний раунд. В этом раунде игроки также не подвергаются наказанию за отступничество, так как в любом случае они собираются отступиться в последнем раунде. Так что они отступаются в предпоследнем раунде. Но это означает, что они не рискуют быть наказанными в предпредпоследнем раунде и отступаются и в нем. Мы можем прошагать так по дереву игры до первого раунда. Поскольку в этом раунде сотрудничество не является равновесной по Нэшу стратегией, принцип «зуб за зуб» больше не является стратегией РН в повторяющейся игре, и мы получаем тот же результат — взаимное отступничество, — что и при однократной ДЗ. Поэтому сотрудничество возможно только в повторяющихся ДЗ, где ожидаемое количество повторений не определено. (Разумеется, это относится ко многим играм в реальной жизни). Заметьте, что в этом контексте любой объем неопределенности ожиданий или возможность дрожащей руки будут способствовать сотрудничеству, по крайней мере, некоторое время. Когда люди в экспериментах играют повторяющиеся ДЗ с известным числом ходов, они действительно склонны сотрудничать некоторое время, но потом, с опытом, научаются отступаться чуть раньше.

Теперь введем второе осложнение.

Предположим, что способность игроков отличать отступничество от сотрудничества несовершенна. Рассмотрим наш случай картеля штуковин. Предположим, что игроки наблюдают падение рыночной цены на штуковины. Возможно, это объясняется обманом одного из членов картеля. Или, возможно, это вызвано экзогенным падением спроса. Если руководствующиеся принципом «зуб за зуб» игроки ошибочно примут второе за первое, они нарушат договоренность, тем самым вызвав цепную реакцию взаимных отступничеств, из которой они никогда не смогут выбраться, поскольку каждый игрок будет отвечать на первое обнаруженное отступничество взаимностью, тем самым инициируя дальнейшие, и т.д.

Если игроки знают, что такое недопонимание возможно, у них есть стимул прибегнуть к более сложным стратегиям. В частности, они могут быть готовы иногда рисковать после нарушений и вновь кооперироваться, чтобы проверить свои выводы. Однако, если они слишком благосклонны, тогда другие игроки могут использовать это и отступиться снова. В общем, сложные стратегии сталкиваются с проблемой. Поскольку другим игрокам сложнее их прочесть, использование сложных стратегий увеличивает вероятность взаимного недопонимания. Но недопонимание приводит к развалу кооперативных равновесий в повторяющихся играх. Сложности, связанные с передачей информации, ее оценкой и выводами в повторяющихся ДЗ помогают интуитивно объяснить народную теорему, называемую так, потому что никто не знает наверняка, кто первый ее сформулировал. Согласно этой теореме в повторяющихся ДЗ для любой стратегии S существует такое распределение стратегий других игроков, что вектор S и этих стратегий является РН. Так что ничего особенного в принципе «зуб за зуб» на самом деле нет.

Реальные, сложные, социальные и политические драмы редко бывают реализациями простых игр типа ДЗ. Хардин (Hardin 1995) анализировал два трагически реальных политических кейса: гражданской войны в Югославии 1991–1995 годов и геноцида в Руанде в 1994 году как ДЗ, которые были встроены в координационные игры.

Координационная игра возникает всякий раз, когда полезность двух или более игроков максимизируется тем, что они делают одно и то же, и когда сам по себе факт наличия такой согласованности им важнее, чем содержательная сторона того, что они оба делают. Стандартный пример заимствуется из правил дорожного движения: «все движение левостороннее» и «все движение правостороннее» являются РН, и ни одно из них не эффективнее, чем другое. В играх с «чистой» координацией не помогают даже более точные критерии равновесия.