физика

Поделиться статьей в социальных сетях:

в избранное

Принцип соответствия Бора

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 14 октября 2010 года.

По поводу принципа соответствия Нильса Бора историк физики Макс Джеммер пишет следующее: «В истории физики найдется немного примеров всеобъемлющих теорий, столь многим обязанных одному принципу, сколь обязана боровскому принципу соответствия квантовая механика» (Джеммер 1985: 124). Этот принцип не только сыграл ключевую роль в открытии самой квантовой механики, но и послужил для Бора краеугольным камнем ее философской интерпретации, будучи тесно связанным с его более известным принципом дополнительности и копенгагенской интерпретацией.

Хотя большинство исследователей не подвергают сомнению важность принципа соответствия Бора, они расходятся во мнениях относительно того, как этот принцип следует определять. Следует различать смысл, который приписывал ему сам Бор, и значение, которое он позднее обрел для более широкого сообщества физиков. Даже если ограничиться только сочинениями Бора, среди исследователей по-прежнему нет единого мнения по поводу того, какое именно из нескольких соотношений между классической и квантовой механикой, открытых Бором, должно быть обозначено как принцип соответствия. В специальной литературе имеется три основных кандидата на роль определения. Во-первых, это частотная интерпретация, согласно которой в принципе соответствия речь идет о статистическом асимптотическом совпадении значений одного члена в преобразовании Фурье классической частоты, с одной стороны, и квантовой частоты в пределе больших квантовых чисел, с другой. Во-вторых, имеется интерпретация по интенсивности, согласно которой принцип соответствия постулирует статистическое совпадение (в пределе больших квантовых чисел) значений квантовой интенсивности, выраженной посредством вероятности квантового перехода, и классической интенсивности, понятой как квадрат амплитуды одной компоненты классического движения. Наконец, существует интерпретация по правилу отбора, согласно которой принцип Бора, по сути, утверждает, что каждый разрешенный квантовый переход между стационарными состояниями соответствует одной гармонической компоненте классического движения.

Принцип соответствия впервые был сформулирован в 1913 году в контексте старой квантовой теории. Тем не менее, по словам Бора, этот принцип сумел пережить замещение старой квантовой теории современной квантовой механикой. Принцип соответствия до сих пор фигурирует в литературе по физике как предмет текущих исследований, хотя, по всей видимости, его значение несколько отличается от смысла, который ему придавал сам Бор. Одна из разновидностей принципа соответствия также нашла место в философской литературе, где была обобщена до уровня базового методологического принципа (т.н. обобщенного принципа соответствия), накладывающего ограничения на развитие новых научных теорий.

Предыстория и научный контекст

Нильс Бор — датский физик, живший с 1885 по 1962 год; родился и умер в Копенгагене. Он наиболее известен как один из основоположников квантовой теории. Бор также прославился работой о строении атомов — в 1922 году благодаря ей он получил Нобелевскую премию по физике. Помимо научных изысканий Бор посвятил большую часть своей карьеры философской интерпретации квантовой механики. Он участвовал в знаменитой продолжительной дискуссии с Альбертом Эйнштейном по поводу того, является ли квантовая механика полным описанием атомных явлений (т.н. дискуссия Эйнштейна–Бора). Плоды его трудов по истолкованию квантовой теории включают в себя копенгагенскую интерпретацию, положение о дополнительности и принцип соответствия.

Принцип соответствия впервые был предложен в контексте старой квантовой теории, разработанной в период между 1900 и 1925 годами. Старая квантовая теория была «промежуточной» теорией — она возникла в качестве реакции на признание непригодности ньютоновской механики и классической электродинамики для описания атомных систем. Хотя старая квантовая теория имела немалый эмпирический успех, ее критиковали за несовместимые, как казалось многим, основания. Старая квантовая теория в конечном итоге была замещена современной квантовой механикой благодаря матричной механике, разработанной Вернером Гейзенбергом в 1925 году, а также волновой механике, выдвинутой Эрвином Шрёдингером в 1926 году.

Чтобы понять суть принципа соответствия, необходимо сначала рассмотреть основные положения старой квантовой теории. Нильс Бор впервые сформулировал ее постулаты в 1913 году в трехчастной работе «О строении атомов и молекул» (Bohr 1913; Бор I: 84–148). Бор принял модель атома Эрнеста Резерфорда, согласно которой основная часть массы атома сосредоточена в небольшом центральном ядре, а электроны вращаются вокруг ядра по планетарным траекториям. Главная проблема модели Резерфорда заключалась в нестабильности: согласно классической электродинамике, электрон, являющийся ускоренным заряженным телом, должен излучать энергию и, следовательно, вскоре упасть на ядро. Решение Бора состояло в том, чтобы встроить в модель Резерфорда теорию излучения Макса Планка, которая постулирует, что «излучение энергии атомной системы происходит не непрерывно (как принято в классической электродинамике), а, напротив, определенными раздельными актами испускания» (Bohr 1913: 4; BCW 2: 164; Бор I: 87) {{1}}.

Бор кратко сформулировал свою квантовую теорию при помощи двух допущений, или постулатов. В соответствии с первым постулатом, электроны не могут вращаться вокруг ядра по какой угодно траектории. Вернее будет сказать, что атомные системы могут существовать лишь в виде последовательности дискретных «стационарных состояний», в которых электрон находится на особой разрешенной и устойчивой периодической орбите и при этом не испускает излучение. Такие состояния могут быть наглядно представлены как ряд концентрических круговых орбит, вдоль которых движется электрон. Cтационарные состояния пронумерованы главным квантовым числом n, где наименьшая разрешенная орбита («нормальное» или основное состояние) обозначена n = 1, следующее состояние с более высокой энергией — n = 2 и т.д. Согласно Бору, когда электрон находится в одном из стационарных состояний, его перемещения могут быть адекватно описаны с помощью классической механики, однако когда электрон совершает переход из одного стационарного состояния в другое, классическая теория оказывается уже не пригодной. Второй постулат старой квантовой теории Бора состоит в том, что при переходе между различными стационарными состояниями (n' и n") испускаемое излучение имеет одну частоту (ν), определяемую через разность энергий двух состояний (En' – En"), деленную на постоянную Планка.

ν = (En' – En") / h

(1)

Эта формула обычно называется правилом частот Бора–Эйнштейна. Второй постулат представляет собой значительный разрыв с классической электродинамикой, согласно которой испускаться будет многообразие различных частот излучения и эти частоты будут определяться исключительно движением источника.

Важно отметить: пускай сегодня принято считать, что испускаемое излучение является фотоном, сам Бор, как ни странно, довольно скептически относился к концепции фотонов вплоть до середины 1920-х годов (Stachel 2009). Бор предпочитал рассматривать излучаемое или поглощенное излучение как волну, а не частицу. Сопротивление Бора принятию существования фотонов в этот период, по всей видимости, обусловлено ​​его опасением, что представление о частицах света окажется не в состоянии объяснить известные явления интерференции. К примеру, Бор пишет в 1921 году следующее:

Любопытно, что первоначальный отказ Бора от концепции фотона был вызван насущной необходимостью анализировать излучение в его гармонических компонентах в целях применения его принципа соответствия (см. ниже). Как отмечает Джон Стэйчел: «Действительно, похоже, что Бор не доверял понятию фотона главным образом из-за своей зависимости от принципа соответствия и связанной с ней готовностью отказаться от сохранения энергии-импульса для того, чтобы спасти представления об излучении классической электродинамики» (Stachel 2009: 72). Стэйчел утверждает, что Бор был вынужден в конечном итоге принять теорию фотона, помимо прочего, из-за результатов экспериментов Боте–Гейгера и Комптона–Саймона. В силу описанных исторических причин необходимо проявлять осторожность при обращении к понятию фотона в ходе рассмотрения ранних взглядов Бора. Тем не менее, концепция фотонов весьма полезна для понимания физики, обуславливающей принцип соответствия (и представления Бора после начала 1920-х), и потому она будет использована в последующем изложении.

Вернемся к намеченной нами схеме старой квантовой теории: двух постулатов Бора еще недостаточно для того, чтобы выбрать из всех классически разрешенных орбит те, которые соответствуют стационарным состояниям. Чтобы определить стационарные состояния, необходимо также ввести следующее «квантовое условие»:

∮pθdθ = nh,

(2)

где интеграл по замкнутому контуру берется за один период электронной орбиты, р — угловой момент (радиальная составляющая), θ — угол в плоскости электронной орбиты, а n — квантовое число {{2}}. Как подытоживает Макс Джеммер, применение старой квантовой теории состоит, по сути, из трех этапов: «…во-первых, [из] использования классической механики для определения возможных движений системы; во-вторых, наложения определенных квантовых условий для отбора фактических или разрешенных движений; в-третьих, рассмотрения радиационных процессов как переходов между разрешенными движениями, подчиняющихся условию частот Бора» (Джеммер 1985: 97). Старая квантовая теория складывалась из сочетания классических и квантовых идей: хотя предполагается, что движение электрона в определенном стационарном состоянии все еще можно описать на основе классической теории, излучение, выделяемое при переходе между стационарными состояниями («квантовые скачки»), классически описать уже нельзя.

Понять содержание принципа соответствия поможет взгляд на упрощенную модель атома как одномерной системы, где электрон совершает простое периодическое движение. В классической физике траектория электрона задается выражением x(t), которое выступает решением уравнения движения Ньютона, и является периодической. Это значит, что электрон просто снова и снова повторяет свой путь с частотой ω, известной как основная частота. Поскольку движение является периодическим, положение электрона может быть представлено в виде ряда Фурье следующим образом {{3}}:

x(t) = C1cos(ωt) + C2cos (2ωt) + C3cos(3ωt) + …

(3)

Каждый из этих членов в сумме называется гармоническим, а τ-я гармоника задается через время t, амплитуду Cτ, и частоту ωτ, которая является целым кратным основной частоты, ωτ = τω (эти кратные основной частоты называются обертонами). Согласно классической электродинамике, частоты излучения, испускаемого данным атомом, должны быть заданы только в частотах гармоник движения: ω, 2ω, 3ω и т.д.; вот почему спектр данной классической системы должен представлять собой ряд дискретных и равноудаленных линий.

Напротив, согласно старой квантовой теории Бора, излучение возникает вовсе не из-за ускоренного движения электрона по орбите, а из-за «перескакивания» электрона из одного стационарного состояния в другое; и вместо того, чтобы выделялись все гармонические «обертоны» вместе, испускается только одна частота ν, чье значение задается правилом частот Бора–Эйнштейна (см. уравнение 1). Спектральные линии создаются целым ансамблем атомов, осуществляющих переходы между различными стационарными состояниями, и хотя в этих линиях можно усмотреть закономерность, расположены они не равноудаленно — за исключением случая пределов больших квантовых чисел.

Вслед за Бором можно обозначить разницу между стационарными состояниями n’ и n” через τ — т.е. если электрон переходит в ближайшее (к n’) стационарное состояние, τ = 1; если он перепрыгивает два стационарных состояния, τ = 2, и т.д. Хотя в соответствии с классическим определением τ обозначает конкретную гармоническую компоненту классического движения, согласно квантово-механическому определению τ указывает на изменение квантового числа в конкретном скачке.

Определения принципа соответствия

Большинство современных исследователей, занимающихся изучением работ Бора, пришли к выводу, что сам Бор вовсе не предполагал, будто его принцип соответствия установит некое общее требование, согласно которому квантовая механика должна воспроизводить предсказания классической механики в классическом пределе. Однако именно данная интерпретация преобладает в физике (см. раздел 6). При этом нет единого мнения касательно вопроса о том, какое именно соотношение между классической и квантовой механикой Бор намеревался установить при помощи своего принципа. В специальной литературе были предложены три многообещающих варианта ответа, каждому из которых можно найти подтверждение в сочинениях Бора. Эти три трактовки могут быть обозначены как частотная интерпретация, интерпретация по интенсивности и интерпретация по правилу отбора.

В рамках частотной интерпретации принцип соответствия определяется как статистическое асимптотическое совпадение значений (квантовой) частоты νn' → n" излучения, испускаемого при квантовом скачке разности τ из состояния n′ в n″, и (классической) частоты ωτ в τ-й гармонике классического движения в стационарном состоянии n′, а именно:

νn' → n" = ωτ = τω при больших n,

(4)

где n' – n" = τ.

Заметим, что о равенстве между квантовой частотой и одной компонентой классической частоты можно говорить только в пределе больших квантовых чисел — оно неприменимо для низкоуровневых квантовых переходов. Более того, речь можно вести лишь о статистическом совпадении, поскольку в классическом рассмотрении все частоты будут выделяться вместе, тогда как в рамках квантово-механического подхода испускается только один фотон с одной частотой при любом заданном переходе между стационарными состояниями. Следовательно, необходимо сопоставить статистический ансамбль атомов с классическим спектром.

Согласно интерпретации по интенсивности, принцип соответствия определяется как совпадение (в пределе больших квантовых чисел) вероятности Pn'→ n" перехода между двумя стационарными состояниями, разделенными τ и квадратом амплитуды (Cτ) τ-й гармонической компоненты классического движения:

Pn'→ n" ∝ |Cτ(n)|2 при больших n

(5)

Таким образом, в пределе больших n амплитуды гармонических компонент классической орбиты электрона могут быть использованы для расчета интенсивностей спектральных линий. В то время как при классическом рассмотрении интенсивность излучения определяется его амплитудой, в рамках квантово-механического подхода интенсивность спектральной линии определяется числом фотонов, испускаемых на этой конкретной частоте. Следовательно, чем вероятнее конкретный квантовый переход, тем больше фотонов будет выделено и тем большей окажется интенсивность. Заметим, что это соответствие, как и при частотной интерпретации, наблюдается только статистически и лишь в пределе больших квантовых чисел {{4}}.

В рамках интерпретации по правилу отбора принцип соответствия Бора рассматривается прежде всего как утверждение, что каждый разрешенный квантовый переход между стационарными состояниями соответствует одной гармонической компоненте классического движения. Если быть более точным, правило отбора Бора гласит: переход из стационарного состояния n′ в другое стационарное состояние n″ допускается тогда и только тогда, когда существует τ-я гармоника в классическом движении электрона в начальном стационарном состоянии; если τ-й гармоники в классическом движении нет, то переходы между стационарными состояниями, отстоящими друг от друга на τ, квантово-механически не допускаются. Суть принципа соответствия Бора отображена на рис. 1.

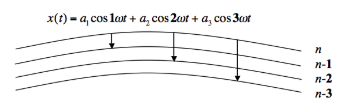
Рис. 1. Классическая периодическая орбита x(t) может быть представлена в виде суммы Фурье, «гармоники» которой являются целыми кратными основной частоты ω, представляющей периодичность движения. В рамках интерпретации по правилу отбора принцип соответствия является догадкой Бора, согласно которой каждый разрешенный переход между стационарными состояниями соответствует одной гармонической компоненте классического движения. (На основании рис. 3 из Fedak and Prentis 2002.)

Правило отбора можно проиллюстрировать следующим упрощенным примером{{5}}

Предположим, что решение уравнения Ньютона F = m d2x/dt2 и квантовое условие ∮pdx = nh представляют собой{{6}}

x(t,n) = ncos(n½t) + n½cos(3n½t),

(6)

т.е. разложение в ряд Фурье классического периодического движения электрона в разрешенном стационарном состоянии n. Для этого стационарного состояния n основная частота (периодичность движения электрона) представляет собой ω = n½. Отметим, что в классическом движении присутствуют только первая (τ = 1) и третья (τ = 3) гармоники (см. уравнение 6). По правилу отбора Бора, отсюда следует, что квантовые скачки могут происходить только между стационарными состояниями, удаленными друг от друга на одно или три стационарных состояния. Так, например, возможны переходы из стационарного состояния n = 100 в стационарные состояния n = 99 или n = 97; однако переход из n = 100 в стационарное состояние n = 98 невозможен, так как на классической электронной орбите нет второй гармоники.

В отличие от интерпретаций принципа соответствия по частоте или интенсивности, трактовка, опирающаяся на правило отбора, не включает асимптотическое отношение — она применима к переходам между любыми квантовыми числами, включая малые n.

Важно принять к сведению, что Бор открыл все эти отношения соответствия и написал о них; разногласие между исследователями работ Бора касается лишь того, какое из этих соответствий Бор намеревался обозначить в качестве предмета принципа соответствия. Некоторые исследователи даже начали сомневаться в наличии у Бора четкого и неизменного определения последнего. Эти и другие интерпретации принципа подробно описываются в нижеследующем разделе 5.

Сочинения Бора о принципе соответствия (1918–1928)

Большинство сочинений Бора о принципе соответствия собраны в третьем томе «Избранных трудов Нильса Бора» (Niels Bohr Collected Works, далее BCW), носящем название «Принцип соответствия (1918–1923)» (The Correspondence Principle [1918–1923]). Как пишет сам Бор (Bohr 1922), первый зародыш принципа соответствия обнаруживается в его лекции 1913 года «О строении атомов и молекул» (Бор I: 84–148), хотя данный термин не фигурирует в работах до 1920 года. До того, как он ввел выражение «принцип соответствия», Бор описывал отношение, составляющее содержание принципа, как аналогию между классической и квантовой механикой. Например, в статье 1918 года «О квантовой теории линейных спектров» (которую он называет «работой I») Бор пишет: «Представляется возможным пролить свет на исключительные трудности, если попытаться проследить аналогию между квантовой теорией и классической теорией излучения как можно тщательнее» (Bohr 1918: 4, BCW 3: 70). Однако в более поздних работах Бор явно отвергает точку зрения, согласно которой принцип соответствия можно рассматривать как аналогию:

В работе I это название еще не используется, но содержание принципа формулируется там как формальная аналогия между квантовой и классической теориями. Однако такая формулировка могла быть источником ошибок, поскольку, как мы увидим в дальнейшем, принцип соответствия должен рассматриваться как чисто квантово-теоретический закон, который никоим образом не может уменьшить контраст между этими постулатами и классической электродинамикой. (Bohr [1923] 1924: 22fn1; Бор I: 505п1)

Здесь Бор не только отвергает мнение, будто принцип соответствия — это аналогия. Само указание на принцип как на закон квантовой теории подразумевает, во-первых, что Бор считает его всеобщим принципом (а не применимым лишь в узкой области), и, во-вторых, что он выступает неотъемлемой частью самой квантовой теории, нежели разновидностью общего методологического ограничения, привносимого в квантовую теорию извне.

В статье 1920 года «О сериальных спектрах элементов», где впервые появляются термины «соответствие» и «принцип соответствия» (Nielsen 1976: 21), Бор пишет:

Здесь Бор описывает соответствие между разрешенными переходами из одного стационарного состояния в другое и гармоническими компонентами классического движения. Более того, он считает это соответствие обоснованием или оправданием представления о том, что квантовая теория является рациональным обобщением классической механики (разбор этой точки зрения см. в Bokulich and Bokulich 2005). Спустя несколько страниц Бор переходит к описанию соответствия как частот, так и интенсивностей:

Задаваясь вопросом о более глубоком значении найденного соответствия, мы вправе, естественно, ожидать, что соответствие не ограничивается совпадением частот спектральных линий, вычисленных тем и другим методом, но простирается и на их интенсивности. Такое ожидание равносильно гому, что вероятность определенного перехода между двумя стационарными состояниями связана известным образом с амплитудой, соответствующей гармонической компоненте. Дальнейшее рассмотрение приводит нас к тому, что эта своеобразная связь является общим законом переходов между стационарными состояниями; мы должны предположить, что возможность перехода между двумя данными стационарными состояниями связана с наличием определенной гармонической компоненты в движении системы. (Bohr 1920: 27–28; BCW 3: 249–250; Бор I: 253–254)

В свойственном ему духе Бор не может четко объявить, что именно собирается обозначить в качестве предмета принципа соответствия: одно из этих соответствий, все или ни одно из них.

Бор также утверждает, что принцип соответствия объясняет, почему в экспериментах наблюдаются только определенные спектральные линии. Он пишет:

Приведенный выше взгляд, который можно назвать принципом соответствия <…> позволяет предложить непосредственное истолкование кажущейся своенравности, связанной с применением комбинационного принципа спектральных линий и заключающейся в том обстоятельстве, что лишь малая часть спектральных линий, наличие которых можно было бы ожидать в силу неограниченного применения данного принципа [Ридберга–Ритца], на самом деле наблюдается в экспериментах. (Bohr 1921b, неопубл., BCW 4: 150)

Как утверждает Бокулич (Bokulich 2008), интерпретация принципа соответствия с опорой на правило отбора проясняет не только утверждение Бора, согласно которому этот принцип объясняет своенравность спектральных линий, но и его заявление о том, что принцип соответствия выступает в качестве закона квантовой теории. Действительно, соответствие, которое Бор называет «законом», — это соответствие по правилу отбора, которое справедливо для малых квантовых чисел, а не только в классическом пределе. Это закон, поскольку речь идет о всеобщем (т.е. применимом ко всем n) ограничении, накладываемом на разрешенные квантовые переходы. Будет легче понять, почему это закон именно квантовой теории (а не классической электродинамики), если рассмотреть следующие замечания Бора:

Очевидно, что Бор считает квантовую механику универсальной теорией. Несмотря на статистическое совпадение результатов в классическом пределе, физика, на которую опираются понятия, к примеру, «частоты» и «интенсивности», остается различной. При этом Бор настаивает, что именно квантовый подход является верным в строгом смысле — даже при таком большом значении n, или «классическом» пределе. Следовательно, когда Бор обнаружил, что разрешенными являются те квантовые переходы, для которых имеется соответствующая гармоника в классическом движении, его открытие касалось самой квантовой теории.

В гёттингенских лекциях 1922 года по атомной теории Бор вновь подчеркивает, что принцип соответствия справедлив даже для переходов с небольшим квантовым числом. В частности, об этом свидетельствует его обсуждение хорошо известных красных и зеленых линий серии Бальмера в видимой части спектра водорода. Красная линия (которая действительно имеет красный цвет с длиной волны около 656 нм), обычно обозначаемая Hα, возникает из-за излучения, испускаемого при скачке от стационарного состояния n = 3 до n = 2. Зеленая линия (обозначаемая Hβ, с длиной волны около 486 нм) является результатом скачка электрона в атоме водорода от стационарного состояния n = 4 до n = 2.

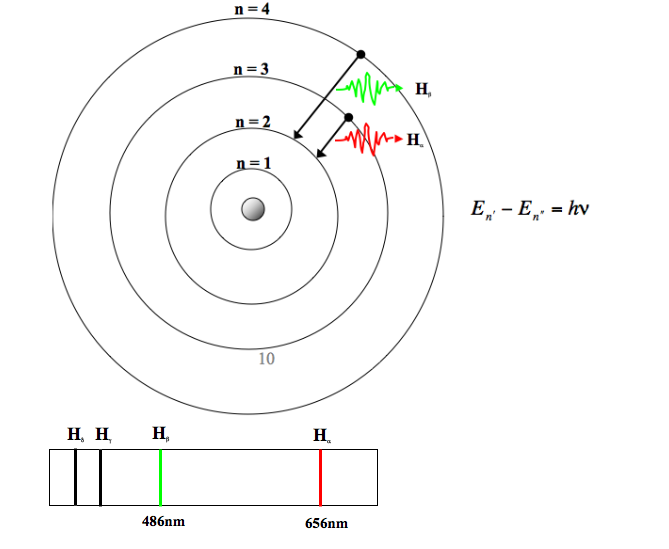
По поводу данных переходов с низким квантовым числом Бор пишет:

Мы можем рассматривать Hβ как октаву Hα, поскольку Hβ соответствует скачку на 2, а Hα — квантовому скачку на 1. Верно, что частота Hβ не превышает частоту Hα в два раза, однако она соответствует октаве. Это отношение мы называем принципом соответствия. Каждому переходу соответствует гармоническая компонента механического движения. (Bohr 1922, неопубл. лекция; BCW4: 348)

Иными словами, хотя при низких квантовых числах «соответствие частот» не наблюдается (и интенсивности линий нельзя рассчитать непосредственно из классических амплитуд по «соответствию интенсивностей»), по-прежнему в силе то, что Бор называет здесь более общим принципом соответствия. В частности, переходы τ = 1 и τ = 2 допустимы, поскольку в преобразовании Фурье классической орбиты электрона в начальном стационарном состоянии есть первая и вторая гармонические компоненты. Фрагменты, подобные приведенной цитате, делают затруднительной интерпретацию принципа соответствия как разновидности асимптотического отношения, которое проявляется в классическом пределе.

В заявлениях Бора о принципе соответствия просматривается преемственность. В 1923 году Бор вновь подчеркивает: разрешенные (или возможные) переходы между стационарными состояниями связаны с гармоническими компонентами, присутствующими в классическом движении.

…возможность перехода между двумя стационарными состояниями многократно периодической системы, характеризующимися квантовыми числами соответственно n1', … nu' и n1", … nu", сопровождающегося излучением, обусловлена теми гармоническими компонентами колебания в выражении (2) [разложение в ряд Фурье классического движения электронов], для которых частота τ1ω1 + … + τuωu удовлетворяет соотношениям

τ1 = n1′ − n1″, …, τu = nu′ − nu″.

Поэтому такие компоненты мы назовем «соответствующими» компонентами колебаний, а сущность приведенного выше рассуждения — «принципом соответствия» для многократно периодической системы. (Bohr [1923] 1924: 22; BCW 3: 479; Бор I: 505)

В 1925 году Вернер Гейзенберг публикует свою знаменитую статью «О квантово-теоретическом истолковании кинематических и механических соотношений», где представляет матричную механику (Heisenberg 1925, Гейзенберг 1977). Она положит начало современной квантовой механике, которая заменит старую квантовую теорию. В приложении к публикации в журнале Nature за декабрь 1925 года Бор описывает свое понимание связи новой квантовой механики с принципом соответствия. Он начинает с утверждения о принципе соответствия:

В этой цитате Бор отмечает все три отношения соответствия: соответствие по правилу выбора, асимптотическое соответствие частот и асимптотическое соответствие интенсивностей. Затем Бор обращается к статье о матричной механике Гейзенберга и утверждает следующее:

Она [новая матричная механика] оперирует совокупностями количеств, которые замещают составляющие гармонического колебательного движения и символизируют вероятности переходов между стационарными состояниями, в согласии с принципом соответствия. <…> Короче говоря, весь аппарат квантовой механики можно рассматривать как точную формулировку тенденций, заключенных в принципе соответствия. (Bohr 1925: 852; BCW 5: 280; Бор II: 22–23)

Мысль Бора в этом отрывке, судя по всему, состоит в том, что способ обозначения (или «символизации») разрешенных переходов в новой квантовой механике согласуется с его правилом отбора.

Бор продолжал обсуждать принцип соответствия даже после появления современной квантовой механики. Например, в «Квантовом постулате и новейшем развитии атомной теории» (лекция в Комо, прочитанная в 1927-м и опубликованная в 1928-м году) он утверждает:

Обратите внимание, что здесь Бор говорит о «символическом» применении классической электродинамики — например, электронные траектории в стационарных состояниях не должны истолковываться буквально или даже «формально». Этот сдвиг в понимании Бором статуса траекторий электронов, фигурирующих в принципе соответствия, подчеркивается, в частности, Оливье Дарриголем (Darrigol 1997: 558).

Тем не менее, после замещения старой квантовой теории современной квантовой механикой в 1928 году Бор все еще трактует соответствие в качестве связи между процессами перехода и гармониками в классическом движении частиц — как и ранее в 1920 году, когда он впервые ввел принцип соответствия. Более того: как и прежде, он прямо соотносит принцип соответствия со своим воззрением, согласно которому квантовая механика представляет собой рациональное обобщение классической механики. Тем самым принцип соответствия обеспечил схождение понятий классической механики (и электродинамики), старой квантовой теории и современной квантовой механики. Тезис о рациональном обобщении, в свою очередь, выступил в качестве опоры для представлений Бора о дополнительности и, в более широком смысле, копенгагенской интерпретации квантовой механики. Таким образом, принцип соответствия оказался не только технически значим для развития современной квантовой механики, как подчеркивает Джеммер (1985: 124), но также лег в само основание философии Бора.

Ранние отклики

Людей, которые первыми откликнулись на принцип соответствия Бора, можно условно разделить на три группы: тех, кто неправильно понял принцип (как Макс Борн и Леон Розенфельд), тех, кто его принял и развил (как Хендрик Крамерс и Джон ван Флек), и тех, кто вроде бы понимал принцип, но все же сомневался в нем (как Арнольд Зоммерфельд, Вольфганг Паули и Вернер Гейзенберг).

Остается неясным, насколько хорошо многие современники Бора понимали, что он имел в виду, говоря о принципе соответствия. К примеру, даже Розенфельд, один из ближайших учеников и коллег Бора, вспоминает, как последний был раздосадован тем, что Розенфельд не сумел верно понять суть принципа (Rosenfeld [1973] 1979: 690). Быть может, это не столь неожиданно, если учесть туманный характер сочинений Бора. Сам Бор прекрасно осознавал тот факт, что его плотный стиль письма зачастую вводил читателей в заблуждение. В письме к Зоммерфельду Бор сетует: «В течение последних нескольких лет я нередко ощущал научное одиночество, находясь под впечатлением, что мои попытки в полную меру своих возможностей выстроить систему из принципов квантовой теории встретили крайне мало понимания… Я прекрасно понимаю, сколь мало все эти вопросы прояснены на текущий момент и сколь я бессилен в выражении своих мыслей в легкой и доступной форме» (Бор — Зоммерфельду, 30 апреля 1922 года; BCW 3: 39).

Действительно, как можно легко заметить, в литературе по физике возник широкий набор различных интерпретаций принципа Бора, которые дают о себе знать и по сей день. А значит, не следует путать смысл, который принципу соответствия придавал сам Бор, и значение, которое этот принцип обрел для более широкого физического сообщества. Например, Крамерс и ван Флек воспользовались термином «принцип соответствия» с тем, чтобы обозначить целый ряд аргументов, которые были выстроены вокруг различного рода соответствий и оказали влияние на развитие квантовой механики (см., напр., Duncan and Janssen 2007).

Среди тех, кто, по всей видимости, верно понимал суть принципа соответствия Бора, еще меньше было тех, кто его принимал. В самом деле, многие из современников Бора выражали свои сомнения по поводу этого принципа, даже несмотря на готовность c выгодой для себя использовать его для получения осязаемых результатов в том случае, если другие методы не работают. В эту группу попадают три наиболее значительных современника Бора, которые выступили с критикой принципа соответствия: Зоммерфельд, Паули и Гейзенберг  {{7}}

Зоммерфельд

Одним из первых и самых рьяных критиков принципа соответствия Бора был Арнольд Зоммерфельд (1868–1951). Из подробного изложения Дарриголя мы узнаём, что Зоммерфельд никогда не соглашался с принципом соответствия Бора полностью и признавал его продуктивность с неохотой (Darrigol 1992: 138–145). Зоммерфельд предпочитал рассматривать квантовую теорию как самодостаточный набор формальных правил и стремился получить правила отбора «при помощи подчеркнуто строгого способа вывода, напоминающего неопровержимую логику численных расчетов» (Sommerfeld [1919] 1923: 265–266). В первом издании своей книги «Строение атома и спектры» (Atombau und Spektrallinen; рус. пер. издания 1951 года см. в Зоммерфельд 1956) Зоммерфельд пренебрежительно отзывается о принципе соответствия Бора, именуя его «волшебной палочкой»:

Сформулировав принцип соответствия, Бор заполучил волшебную палочку (которую он сам называет формальным принципом), которая позволяет нам непосредственно применить результаты классической волновой теории в квантовой теории. (Sommerfeld [1919] 1923: 275){{8}}

Во втором издании «Строения атома» Зоммерфельд смягчает критику принципа соответствия, отмечая его огромную продуктивность. В письме Бору от ноября 1920 года Зоммерфельд пишет:

Суман Сет (Seth 2008) утверждал, что недовольство Зоммерфельда по поводу принципа соответствия проистекает не столько из приверженности формальным правилам, как предполагает Дарриголь, но скорее из общего неприятия мышления по аналогии и всего того, что представлялось Зоммерфельду неправомерным смешением квантовых и классических понятий. Подобное недоверие дает о себе знать, к примеру, в статье Зоммерфельда 1924 года, посвященной моделям атома у Бора, где он пишет:

Волшебная сила принципа соответствия доказала себя в целом на примере правил отбора квантовых чисел в спектральных рядах и полосах… Тем не менее, я не могу рассматривать его как окончательно удовлетворительный из-за смешения [в этом принципе] квантово-теоретической и классической точек зрения. (Sommerfeld 1924: 1048; также цит. в Seth 2008: 345)

Критическое отношение Зоммерфельда к принципу соответствия окажет влияние на Паули и Гейзенберга, которые оба защитили диссертации под его научным руководством.

Паули

В лекции по случаю присуждения ему в 1945 году Нобелевской премии за открытие принципа запрета Вольфганг Паули описывает коренные методологические различия подходов Бора и Зоммерфельда:

Хотя по прошествии времени Паули утверждает, что на него повлияли обе методологии, в переписке, датируемой 1924 и 1925 годами, он преимущественно отстаивает подход Зоммерфельда, отбрасывая как принцип соответствия, так и модельные рассуждения в целом. Критические замечания Паули по поводу принципа соответствия Бора сосредотачиваются вокруг двух вопросов. Во-первых, Паули возражал против использования даже «формального» понятия электронной орбиты, играющего главную роль в применении принципа соответствия (напр., Паули — Бору, 21 февраля 1924 года). Во-вторых, Паули сомневался, что принцип соответствия сумеет объяснить заполнение электронных оболочек, как на это надеялся Бор. В 1924 году Паули написал Бору:

Если читать между строк, то, по-видимому, Паули понимает принцип соответствия Бора как правило отбора, касающееся переходов между стационарными состояниями, которые связаны с гармониками в классическом движении. Паули возражает не против данного принципа соответствия, а, скорее, против попыток объяснить с его помощью заполнение групп электронов в атоме — той разновидности расширенного принципа соответствия, которую Паули в других местах называл «империализмом принципа соответствия» (Imperialismus des Korrespondenzprinzips) (Паули — Гейзенбергу, 28 февраля 1925 года; цит. по Serwer 1977: 233). Заполнение электронных оболочек будет в конечном счете объяснено принципом запрета Паули, хотя изначально Паули не был доволен таким объяснением, поскольку нельзя было предоставить более общее обоснование и подтверждение его правила запрета. Когда Бор предположил, что принцип соответствия сумеет обеспечить такое обоснование, Паули в ответ заявил:

Из приведенной выше цитаты следует, что Паули примыкает к Зоммерфельду в своем недоверии к принципу соответствия и всем рассуждениям, основанным на моделях, а также в предпочтении «непосредственной» интерпретации, опирающейся на понятия новой квантовой механики.

Гейзенберг

По словам Джагдиша Мехра и Хельмута Рехенберга (1982), когда Вернер Гейзенберг впервые прибыл в Копенгаген для работы с Бором в 1924 году, он с энтузиазмом принял принцип соответствия и взялся отстаивать его перед более широким сообществом физиков. Это особенно заметно в письме Гейзенберга, адресованному Паули 30 сентября 1924 года:

Тем не менее, к 1925 году Гейзенберг начал все больше дистанцироваться от принципа соответствия. Даниэль Сервер объясняет эту перемену во взглядах влиянием Паули:

Несмотря на то, что он в значительной степени полагался на принцип соответствия при разработке матричной механики, Гейзенберг больше не отстаивал его на публике {{9}}. Действительно, как отметила Мара Беллер, «Гейзенберг вообще не ссылается на работу Бора [в статье 1925 года о матричной механике], хотя статья опиралась на принцип соответствия Бора фундаментальным образом… Вместо этого Гейзенберг [некорректно] заявил, что его заключения вытекают из позитивистского принципа исключения ненаблюдаемых объектов» (Beller 1999: 140){{10}}. Гейзенберг выражает все более противоречивое отношение к принципу соответствия в книге «Физические принципы квантовой теории»:

Гейзенберг готов признать ограниченную полезность данного принципа, однако не рассматривает его как основное положение квантовой теории, в отличие от Бора. Вместо этого Гейзенберг утверждает: «следует подчеркнуть, что это [соответствие представляет собой] чисто формальный результат; он не вытекает из каких-либо физических принципов квантовой теории» (Heisenberg 1930: 83). Другими словами, соответствие должно истолковываться как чисто математический результат, а не как проявление некой глубинной связи между квантовой и классической теориями и уж тем более не как принцип квантовой теории. Для Гейзенберга квантовая механика — это замкнутая теория [Abgeschlossene Theorie], самодостаточная аксиоматическая система, которая никоим образом не зависит от классической механики {{11}}.

Интерпретации историков и философов науки

Судя по всему, любая интерпретация принципа соответствия сталкивается с четырьмя трудностями. Во-первых, нужно определить, какую именно связь (или же сочетание связей) из целого ряда аналогий между классической и квантовой механиками Бор намеревался обозначить в качестве содержания принципа соответствия. Во-вторых, следует установить область действия принципа соответствия (т.е. определить, применяется ли он только к большим квантовым числам или же ко всем). В-третьих, необходимо назвать причину, по которой Бор считал, что принцип соответствия следует рассматривать как закон квантовой теории. Наконец, нужно объяснить, почему Бор полагал, что принцип соответствия был формализован и тем самым сохранен в новой (матричной) квантовой механике.

Один из наиболее влиятельных разборов принципа соответствия Бора представлен в книге Макса Джеммера «Эволюция понятий квантовой механики» (The Conceptual Development of Quantum Mechanics, 1966; см. Джеммер 1985). По мнению Джеммера, принцип соответствия касается взаимосвязи между кинематикой электрона и свойствами испускаемого излучения. Как и многие комментаторы, он уделяет внимание прежде всего отношению частот. Джеммер отмечает, что Бор также обнаружил асимптотическое соответствие интенсивностей спектральных линий и амплитуд в классических гармонических компонентах движения, а также соответствие поляризации испускаемого излучения и характера классического движения. Хотя Джеммер рассматривает и эти соответствия, по-видимому, именно соответствие частот составляет для него главное содержание принципа соответствия. О принципиальной роли данного отношения Джеммер высказывается следующим образом:

Согласно Джеммеру, принцип соответствия, понятый как отношение частот, по указанию применяется ко всем квантовым числам — и, следовательно, получает ранг «принципа», пускай речь идет лишь о «приближенном» отношении, которое является точным только для больших квантовых чисел.

К заявлению Бора о том, что принцип соответствия следует рассматривать как закон квантовой теории, Джеммер относится довольно снисходительно:

По мнению Джеммера, это заявление Бора лишь пытается замаскировать противоречия в основании старой квантовой теории. Несмотря на слова Бора о том, что квантовая теория является рациональным обобщением классической механики, для Бора в понимании Джеммера квантовая и классическая механики несовместимы. И потому Джеммер определяет принцип соответствия как «формальную аналогию, имеющую эвристическое значение». В конце обсуждения принципа соответствия Джеммер заключает: «…многочисленные и часто несколько не согласующиеся друг с другом высказывания Бора о существе принципа соответствия, сделанные им с 1920 по 1961 гг., не дают оснований (если не исключают совсем эту возможность) приписать Бору вполне определенное и неизменное понимание этого принципа» (Джеммер 1985: 123).

Возможно, именно по этой причине Джагдиш Мехра и Хельмут Рехенберг в своем детальном историческом повествовании, посвященном развитию квантовой теории, не занимают твердой позиции относительно того, какое из нескольких обсуждаемых Бором соответствий выступает содержанием его принципа. Как и Джеммер, они пытаются понять, почему Бор считает, что принцип соответствия применим к малым квантовым числам, и почему его следует рассматривать как закон квантовой теории. Они пишут: «Расширение аналогии „неким образом“ до небольших квантовых чисел представляло собой самое дерзкое предположение… [Бор] был уверен, что расширение его соотношений до частот и интенсивностей, справедливое в пределе больших квантовых чисел, может в конечном итоге быть оправдано и тогда, когда речь идет о малых числах» (Mehra and Rechenberg 1982: 250). Мехра и Рехенберг предлагают более подробный разбор этого принципа с технической точки зрения, однако вместе с тем не обсуждают ни заявление Бора о том, что принцип следует рассматривать как закон, ни его утверждение, согласно которому принцип получает формализацию в новой квантовой механике.

Альтернативную интерпретацию принципа соответствия Бора отстаивал Оливье Дарриголь в своей захватывающей и хорошо написанной истории квантовой теории «От классических до квантовых чисел» (From c-Numbers to q-Numbers, 1992). Вместо того, чтобы рассматривать принцип соответствия как утверждение о квантовых и классических частотах, в его интерпретации содержанием принципа оказывается то, что раньше было названо соответствием интенсивностей. Суть последнего заключается в том, что вероятность квантового перехода между двумя стационарными состояниями, отстоящими друг от друга на τ, прямо пропорциональна квадрату модуля классической амплитуды τ-го гармонического колебания, которое в классическом подходе считается мерой интенсивности (см. уравнение 5).

Дарриголь пишет:

Строго говоря, соответствие интенсивностей выполняется точно лишь в пределе больших квантовых чисел, и применить его к малым квантовым числам нельзя. Единственным исключением выступает ситуация, когда классическая амплитуда равна нулю, ведь вероятность квантового перехода также будет равна нулю (частный случай того, что ранее было названо правилом отбора Бора), и это верно для любых квантовых чисел.

В отличие от ряда других интерпретаторов принципа соответствия, Дарриголь полагает, что существует стройное и рациональное объяснение принципа соответствия Бора через соответствие интенсивностей. Он утверждает, что Бор в праве называть его законом квантовой теории, поскольку «речь действительно идет об отношении между двумя квантово-теоретическими понятиями: вероятностью квантового скачка и движением атома» (Darrigol 1997: 553). Более того, Дарриголь убедительно настаивает, что это соответствие было напрямую встроено в матричную механику в статье Гейзенберга 1925 года — тем самым подтверждая слова Бора о том, что новую квантовую механику можно рассматривать как «точную формулировку тенденций, заключенных в принципе соответствия» (Bohr 1925: 852; BCW 5: 280; Бор II: 23).

По словам Дарриголя, несмотря на наличие у Бора этой сквозной темы, в его понимании принципа соответствия все же произошел фундаментальный сдвиг, пускай и неявно:

«Формальность» описания движения электрона в атоме для Дарриголя означает, что в подобном описании сохраняются пространственно-временные и динамические соотношения, хотя уже было признано, что фактически наблюдать подобное движение невозможно. Как только оно стало «символическим» соотношением, описание пространства-времени было полностью утрачено.

Ханс Раддер также утверждал, что понимание Бором принципа соответствия претерпевало развитие на протяжении всей его карьеры. Раддер выделяет три различных этапа. На первом этапе (с 1913 по 1915 годы) принцип соответствия был лишь только «численным соответствием»: речь в нем шла о численном совпадении значений некоторых величин в классической механике (и электродинамике) и старой квантовой теории. На втором этапе, продлившемся с 1916 по 1922 годы, принцип соответствия не только выступал в качестве численного совпадения, но и подразумевал единство понятийного аппарата: «Здесь обе разновидности теории опираются на одни и те же основные понятия ωn,τ и Cn,τ, которые описывают движение электронов по орбитам, и ту же самую функцию f, определяющую вероятности перехода» (Radder 1991: 206). На третьем этапе (1923–1925), завершившемся при создании новой матричной (квантовой) механики, тезис о единстве понятийного аппарата был отклонен Бором в пользу «формального» соответствия. В данном случае под «формальностью» принципа соответствия Раддер имеет в виду нечто иное, чем Дарриголь. По его словам:

Раддер в первую очередь стремится соотнести различные «перевоплощения» принципа соответствия Бора с эвристическими аргументами, претендующими на более общий уровень соответствия, которые были предложены в философии науки (см. раздел 7 ниже).

Среди недавних интерпретаций принципа соответствия Бора можно также отметить позицию Роберта Баттермана. По его словам, «принцип соответствия утверждает, что процессы излучения, к которым применяется второй постулат [hν = E' – E"], образуют „корреляцию“ или приходят в „соответствие“ с механическими колебаниями или периодическими движениями заряженных частиц, — электронов, — в атоме» (Batterman 1991: 203). Как справедливо указывает Баттерман, из принципа соответствия не следует, что квантовая механика должна содержать классическую механику в качестве своего предельного случая. Баттерман настаивает: асимптотическое совпадение классических и квантовых частот (частотная интерпретация) не составляет содержание принципа соответствия, а получает с его помощью него обоснование и объяснение.

В схожем ключе Скотт Танона отвергает мнение о том, что принцип соответствия Бора касается асимптотического совпадения квантовых и классических теорий. По его мнению, принцип соответствия Бора прежде всего устанавливает связь между спектрами (излучения) и орбитальным движением. В более широком смысле Танона утверждает: принцип соответствия следует рассматривать, скорее, не как эвристический инструмент для построения теории, а как теоретико-познавательный (эпистемологический) инструмент, чьей «главной целью в рамках эмпирического подхода Бора было преодоление эпистемологического разрыва между явлениями опыта и неизвестным строением атома… посредством сопоставления классических свойств спектров со свойствами атома» (Tanona 2004: 683).

Относительно недавно Алиса Бокулич выступила с заявлением, что лучше всего принцип соответствия Бора поможет понять указанное ею правило отбора Бора. Оно гласит, что «переход из стационарного состояния n’ в другое стационарное состояние n” допускается тогда и только тогда, когда существует τ-я гармоника в классическом движении электрона в стационарном состоянии; если τ-й гармоники в классическом движении нет, то переходы между удаленными друг от друга на τ стационарными состояниями не допускаются квантово-механически» (Bokulich 2008: 85). При таком прочтении принцип соответствия Бора утверждает, что каждый разрешенный квантовый переход между стационарными состояниями соответствует одной гармонической компоненте классического движения. С точки зрения Бокулич, асимптотические совпадения частот и ​​интенсивностей, отмеченные Джеммером и Дарриголем соответственно, являются приложениями или следствиями принципа соответствия, но не его содержанием. Более того, по ее словам, интерпретация по правилу отбора лучше всего объясняет заявления Бора о том, что принцип соответствия применим к малым n, что он является законом квантовой теории и что он сохраняется в матричной механике в формализованном виде.

Интерпретации, предложенные в современной литературе по физике

Как правило, в современной литературе по физике фигурирует совершенно другое понимание принципа соответствия Бора. Уже в классическом тексте Макса Борна о новой квантовой теории «Атомная физика», впервые опубликованном в 1933 году, можно обнаружить такое определение принципа соответствия:

В литературе по физике приобрели широкое распространение две линии перепрочтения Борном принципа соответствия Бора. Во-первых, речь идет о понимании принципа соответствия как крайне общего требования, по которому квантовая механика должна суметь воспроизвести эмпирические успехи классической механики. Во-вторых, принцип трактуется в качестве более конкретного требования: воспроизведения предсказаний классической механики в пределе больших масс и орбит большой размерности (этот предел обычно выражается в виде n → ∞).

В классическом учебнике Дэвида Бома по стандартной квантовой механике «Квантовая теория» (Quantum Theory, 1951; см. Бом 1965) принцип соответствия в схожем ключе трактуется как общая связь между двумя теориями: «Этот принцип гласит: законы квантовой физики должны быть сформулированы таким образом, чтобы в классических границах, когда в процесс вовлечено много квантов, эти законы приводили бы к классическим уравнениям для усредненных величин» (Бом 1965: 45).

В статье из Physics Today под названием «Пересмотр принципа соответствия» (“The Correspondence Principle Revisited”, 1984) Ричард Либофф утверждает, что принцип соответствия Бора не является общим требованием воспроизвести классическую механики из квантовой — речь идет о более узком заявлении: «…квантовый спектр частот периодической системы приближается к классическому спектру в пределе больших п» (Liboff 1984: 52). Либофф также отмечает, что даже в ограниченной форме принцип соответствия нарушается для таких систем, как частица в ящике и жесткий ротатор. По его словам, «в обоих случаях предел h → 0 приводит к соответствию частот, однако предел n → ∞ не приводит» (Liboff 1984: 52).

Вслед за Либоффом Гази Хасун и Дональд Коуб утверждали, что для получения полноценного классического предела из собственных значений квантовой механики необходимо, чтобы «обе формулировки [принципа соответствия] применялись одновременно в том смысле, что постоянная Планка обратится в нуль, а соответствующее квантовое число уйдет в бесконечность… при условии, что nh = J , где J — релевантное действие классической механики» (Hassoun and Kobe 1989: 658). При таком прочтении принцип понимается просто как предел n→ ∞. Пускай они и называют данный предел «принципом соответствия Бора», авторы все же отмечают, что Бору удалось получить правильную классическую орбитальную частоту как раз «потому, что он не стал брать математический предел там, где квантовое число уходит в бесконечность. Вместо этого Бор счел, что для больших квантовых чисел квантовый результат будет приблизительно классическим. Вот почему квантовое число n, к примеру, может принимать значение n >> 1, но не бесконечно» (Hassoun and Kobe 1989: 661). Хасун и Коуб заключают, что принцип соответствия «часто считается неточным из-за использования Бором больших, но не бесконечных квантовых чисел. Тем не менее, как показано нами, когда формулировки Бора и Планка соединяются, принцип соответствия обретает строгую математическую форму» (Hassoun and Kobe 1989: 661). Так, принцип соответствия рассматривается ими в широком смысле как попытка прийти к математически выверенной формулировке классического предела.

Во многом интерес современного сообщества физиков к принципу соответствия Бора (в его различных пониманиях) заключается в том, что предположительно он не соблюдается в отдельных классах физических систем. Например, в статье «Подчиняется ли квантовая механика принципу соответствия? Является ли она полной?» (“Does Quantum Mechanics Obey the Correspondence Principle? Is It Complete?”) Джозеф Форд и Джорджо Мантика определяют принцип соответствия как требование, по которому «любые две обоснованные физические теории, чьи области применимости пересекаются, с соответствующей точностью должны давать одни и те же прогнозы для наблюдений» (Ford and Mantica 1992: 1087). Авторов занимает вопрос о том, может ли квантовая механика объяснить поведение хаотических классических систем. В схожем ключе для Войцеха Зурека принцип соответствия утверждает согласованность «квантовых и классических математических ожиданий» (Habib et al. 1998). По его мнению, без явления декогеренции принцип соответствия не соблюдается.

В то время как понимание принципа соответствия в современной литературе по физике во многом созвучно указанной выше трактовке Макса Борна, оно отличается от представлений самого Бора. Бор соглашался с тем, что квантовая механика должна суметь воспроизвести эмпирически подтвержденные предсказания классической механики, однако он явным образом отвергал такое прочтение принципа соответствия. Действительно, Леон Розенфельд вспоминает разочарование Бора по поводу того, что его принцип постоянно неверно истолковывали. Когда Розенфельд бесцеремонно предложил Бору вариант, согласно которому принцип соответствия касается асимптотического совпадения квантовых и классических предсказаний, Бор решительно возразил: «Это не аргумент соответствия. Требование, по которому квантовая теория должна переходить к классическому описанию для низких мод колебаний, вовсе не составляет принцип, поскольку оно слишком очевидно» (Rosenfeld 1973: 690).

Обобщенный принцип соответствия

Наконец, важно провести различие между принципом соответствия Бора и тем, что ряд философов науки называет «обобщенным принципом соответствия» (или же «общим принципом соответствия»).

В классическом эссе «Соответствие, инвариантность и эвристики: в защиту консервативной индукции» (“Correspondence, Invariance and Heuristics: In Praise of Conservative Induction”, 1971) Хайнц Пост определяет принцип следующим образом:

Обобщенный принцип соответствия рассматривается здесь как ограничение на развитие новых теорий и как объяснение того, каким образом теории-преемницы связаны со своими предшественницами. Как правило, в физике понятие «вырождения» Поста служит пределом некоего параметра, при достижении которого уравнения теории-преемницы воспроизводятся в качестве предела уравнений теории-предшественницы. При рассмотрении конкретного случая квантово-классического соотношения Пост заявил, что общий принцип соответствия в рамках него не выполняется:

Хотя обобщенный принцип соответствия Поста имеет некоторое сходство с концепцией принципа соответствия Бора, принятой физиками, он довольно сильно расходится с представлениями самого Бора. Действительно, согласно Посту, обобщенный принцип соответствия не выполняется даже для конкретной пары теорий, над которыми работал Бор.

В отличие от Поста, Раддер утверждал, что обобщенный принцип соответствия применим к случаю квантово-классического соотношения (Radder 1991: 215) и что принцип соответствия Бора, понимаемый им в основном как эвристический инструмент, сам может быть рассмотрен в качестве примера обобщенного принципа соответствия (Radder 1991: 208).

Библиография

Работы Бора в русском переводе

[Бор I] Избранные научные труды: В 2 тт. М.: Наука, 1970. Т. 1.

[Бор II] Избранные научные труды: В 2 тт. М.: Наука, 1970. Т. 2.

Бор Н. О строении атомов и молекул // Бор I. С. 84–148.

–—. О сериальных спектрах элементов // Бор I. С. 247–284.

–—. Квантовый постулат и новейшее развитие атомной теории // Бор II. С. 30–53.

Другие первоисточники на русском языке

Бом Д. (1965) Квантовая теория, Москва, Наука.

Борн М. (1970) Атомная физика. М.: Мир.

Гейзенберг В. (1932) Физические принципы квантовой теории. М.; Л.: Государственное технико-теоретическое издательство.

–—. (1977) О квантово-теоретическом истолковании кинематических и механических соотношений // Успехи физических наук. № 122. С. 574–586.

Зоммерфельд А. (1956) Строение атома и спектры: В 2 тт. М.: Государственное издательство технико-теоретической литературы.

Паули В. (1962) Принцип запрета и квантовая механика // Теоретическая физика XX века. Памяти Вольфганга Паули / под ред. Я.А. Смородинского. М.: Издательство иностранной литературы. С. 354–397.

Другие источники на русском языке

Джеммер М. (1985) Эволюция понятий квантовой механики. М.: Наука.

Работы Бора в английском переводе

1913, “On the constitution of atoms and molecules”, Philosophical Magazine, 26: 1–25, 476–502, 857–75.

1918, “The quantum theory of line-spectra”, Det kongelige Danske videnskabernes Selskab, Matematiske-fysike Meddelser, 4(1): 1–36; reprinted in Bohr (1976), pp. 67–102.

1920, “On the series spectra of the elements”, Lecture before the German Physical Society in Berlin (27 April 1920), translated by A. D. Udden, in Bohr (1976), 241–282.

1921a, “Application of the quantum theory to atomic problems in general”, unpublished manuscript in Bohr (1976), pp. 397–414.

1921b, “Constitution of atoms”, unpublished manuscript in Bohr (1977), pp. 99–174.

1922, “Seven lectures on the theory of atomic structure”, unpublished, in Bohr (1977), pp. 341–419.

[1923] 1924, “On the application of the quantum theory to atomic structure,” Proceedings of the Cambridge Philosophical Society (supplement), Cambridge: Cambridge University Press, pp. 1–42. First published in Zeitschrift für Physik, 13 (1923): 117. Reprinted in Bohr (1976), pp. 457–499.

1925, “Atomic theory and mechanics,” Nature (Supplement), 116: 845–852. Reprinted in Bohr (1984), pp. 273–280.

1928, “The quantum postulate and the recent development of atomic theory,” Nature (Supplement), 121: 580–590. Reprinted Bohr (1985), pp. 148–158.

1976, Niels Bohr Collected Works, Vol. 3: The Correspondence Principle (1918–1923), J. R. Nielsen (ed.). Amsterdam: North-Holland Publishing.

1977, Niels Bohr Collected Works, Vol. 4: The Periodic System (1920–1923), J. R. Nielsen (ed.). Amsterdam: North-Holland Publishing.

1984, Niels Bohr Collected Works, Vol. 5: The Emergence of Quantum Mechanics (Mainly 1924–1926), K. Stolzenburg (ed.). Amsterdam: North-Holland Publishing.

1985, Niels Bohr Collected Works, Vol. 6: Foundations of Quantum Physics I (1926–1932), J. Kalckar (ed.). Amsterdam: North-Holland Publishing.

Другие первоисточники на английском и немецком языках

Born, M., 1957 [1933], Atomic Physics, 6th edition. J. Dougall and R. Blin-Stoyle (trans.). New York: Hafner Publishing Co.

Heisenberg, W., 1967 [1925], “Quantum-theoretical re-interpretation of kinematic and mechanical relations”, in B. van der Waerden (ed.), Sources of Quantum Mechanics, New York: Dover Publications, 261–276. Translation of “Über quantentheorische Umdeutung kinematischer und mechanischer Beziehungen”, Zeitschrift für Physik, 33: 879–893.

–––, 1930, The Physical Principles of the Quantum Theory, Translated by C. Eckart and F. C. Hoyt. Chicago: University of Chicago Press.

Pauli, W., 1946, “Exclusion Principle and Quantum Mechanics” in Nobel Lectures, Physics 1942–1962, Amsterdam: Elsevier Publishing Co., 1964.

Sommerfeld, A., 1923 [1919], Atomic Structure and Spectral Lines, translated by H. Brose. London: Methuen.

–––, 1924, “Grundlagen der Quantentheorie und des Bohrschen Atommodelles”, Die Naturwissenschaften 12(47): 1047–1049.

Другие источники на английском языке

Batterman, R., 1991, “Chaos, quantization, and the correspondence principle”, Synthese, 89: 189–227.

Beller, M., 1999, Quantum Dialogue: The Making of a Revolution, Chicago: University of Chicago Press.

Bohm, D., 1951, Quantum Theory, New York: Prentice Hall. Reprinted by Dover Publications, Inc.

Bokulich, A., 2004, “Open or closed? Dirac, Heisenberg, and the relation between classical and quantum mechanics,” Studies in History and Philosophy of Modern Physics, 35: 377–396.

–––, 2006, “Heisenberg meets Kuhn: Closed theories and paradigms”, Philosophy of Science, 73: 90–107.

–––, 2008, Reexamining the Quantum-Classical Relation: Beyond Reductionism and Pluralism, Cambridge: Cambridge University Press.

Bokulich, P. and A. Bokulich, 2005, “Niels Bohr's generalization of classical mechanics,” Foundations of Physics, 35: 347–371.

Darrigol, O., 1992, From c-Numbers to q-Numbers: The Classical Analogy in the History of Quantum Theory, Berkeley: University of California Press.

–––, 1997, “Classical concepts in Bohr's atomic theory (1913–1925)”, Physis: Riv. Internaz. di Storia della Scienza, 34: 545–567.

Duncan, A. and M. Janssen, 2007, “On the verge of Umdeutung, in Minnesota: Van Vleck and the Correspondence Principle, Part One”, Archive for History of Exact Sciences, 61: 553–624.

Fedak, W. A. and J. J. Prentis, 2002, “Quantum jumps and classical harmonics”, American Journal of Physics, 70: 332–344.

Ford, J. and G. Mantica, 1992, “Does quantum mechanics obey the correspondence principle? Is it complete?”, American Journal of Physics, 60: 1086–1098.

Habib, S., K. Shizume, and W. Zurek, 1998, “Decoherence, Chaos and the Correspondence Principle” Physical Review Letters, 80: 4361–4365.

Hassoun, G. and D. Kobe, 1989, “Synthesis of the Planck and Bohr formulations of the correspondence principle”, American Journal of Physics, 57(7): 658–662.

Heilbron, J., 1983, “The Origins of the Exclusion Principle” Historical Studies in the Physical Sciences, 13(2): 261–310.

Liboff, R., 1984, “The correspondence principle revisited”, Physics Today, 37: 50–55.

Mehra, J. and Rechenberg, H., 1982, The Historical Development of Quantum Theory (Volume I: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900–1925; Volume II: The Discovery of Quantum Mechanics 1925), New York: Springer-Verlag.

Nielsen, J. R., 1976, “Introduction to Niels Bohr Collected Works, Vol. 3”, in Bohr (1976), pp. 3–46.

Post, H., 1971, “Correspondence, Invariance and Heuristics: In Praise of Conservative Induction” Studies in History and Philosophy of Science, 2: 213–255. Reprinted in Correspondence, Invariance and Heuristics: Essays in Honour of Heinz Post (Boston Studies in the Philosophy of Science, Volume 148), S. French and H. Kamminga (eds.), Boston: Kluwer Academic Publishers, 1993, pp. 1–43.

Radder, H., 1991, “Heuristics and The Generalized Correspondence Principle”, British Journal for the Philosophy of Science, 42: 195–226.

Rosenfeld, L., 1979 [1973], “The Wave-Particle Dilemma”, in R. Cohen and J. Stachel (eds.) Selected Papers of Léon Rosenfeld (Boston Studies in the Philosophy of Science, Volume 21), Dordrecht: D. Reidel Publishing Co., 688–703. Originally published in J. Mehra (ed.) The Physicist's Conception of Nature, Dordrecht: D. Reidel Publishing Co., pp. 251–263.

Serwer, D., 1977, “Unmechanischer Zwang: Pauli, Heisenberg, and the Rejection of the Mechanical Atom, 1923–1925”, Historical Studies in the Physical Sciences, 8: 189–256.

Seth, S., 2008, “Mystik and Technik: Arnold Sommerfeld and Early-Weimar Quantum Theory”, Berichte zur Wissenschaftsgeschichte, 31(4): 331–352.

Stachel, J., 2009, “Bohr and the Photon” in W. Myrvold and J. Christian (eds.), Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle (Western Ontario Series in Philosophy of Science, Volume 73), Dordrecht: Springer, pp. 69–83.

Tanona, S., 2004, “Idealization and Formalism in Bohr's Approach to Quantum Theory”, Philosophy of Science, 71: 683–695.