физика

Поделиться статьей в социальных сетях:

в избранное

Путешествие во времени и современная физика

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано: 17 сентября 2000 г. (четверг); опубликовано с существенными изменениями: 23 июня 2009 г. (вторник).

Путешествие во времени красной нитью проходит через научную фантастику. С появлением общей теории относительности проблема путешествий во времени серьезно рассматривалась физиками. Но вместе с тем отмечалось, особенно в философской литературе, что путешествия во времени по своей сути парадоксальны. Самый известный парадокс — это так называемый «парадокс дедушки»: вы путешествуете в прошлое, убиваете своего деда и, тем самым, исключаете свое собственное существование. Для того, чтобы избежать некоторых несогласованностей, должно возникнуть некое обстоятельство, из-за которого попытка убить деда окажется неудачной. Не требует ли это некоторого неправдоподобного ограничения для нежелательных обстоятельств? Проверим эти опасения в контексте современной физики.

Неудавшаяся попытка самоубийства

Вы подавлены. У вас депрессия. Вы подавлены настолько, что готовы совершить самоубийство. У вас есть пистолет. Но у вас не хватает смелости направить пистолет на себя и убить себя. Если кто-то другой убьет вас, то это будет хорошо. Но вы не можете попросить кого-то убить вас. Это было бы нечестно. Вы решаете, что если вы остаетесь таким же подавленным и найдете машину времени, то вы совершите путешествие в прошлое, почти к данному моменту, и убьете себя более раннего. Это было бы хорошо. Таким образом вы даже избавитесь от гнетущего времени, которое вы потратите между настоящим моментом времени и моментом, когда вы воспользуетесь машиной времени. Вы начнете размышлять о логичности этой мысли — и вдруг происходит нечто восхитительное. Внезапно вы видите человека, выходящего из никуда, приближающегося к вам с пистолетом, направленным на вас. Он практически похож на вас, но с той лишь разницей, что из его левого глаза вытекает кровь и что он едва ли может встать прямо. Вы спокойны. Вы спокойно смотрите прямо на него. Он стреляет. Вы чувствуете жгучую боль в левом глазу. Ваше сознание спутано. Вы пошатываетесь и случайным образом заходите в странно выглядящую кабинку. Вы погружаетесь в бессознательное состояние. Через некоторое время — и вы не можете понять, сколько прошло времени — к вам возвращается сознание и вы с трудом вылезаете из кабинки. Вы видите человека, смотрящего на вас пристально и спокойно. Вы понимаете, что это вы, но некоторое время назад. Он смотрит прямо на вас. Вы испытываете страшную боль. Вам нужно это закончить — вам нужно убить его. По-настоящему убить его — раз и навсегда. Вы стреляете в него, но ваше зрение настолько плохое, что вы не можете прицелиться. Вы не убиваете его — вы повреждаете его левый глаз. Он, пошатываясь, уходит. Вы падаете на пол от мучительной боли и решаете изучить парадоксы путешествий во времени более серьезно.

Почему при путешествии во времени невозможно совершить самоубийство?

Обычная причина беспокойства, касающаяся путешествий во времени, — это то, что путешествия во времени позволяют кому-либо переместиться в прошлое и убить себя более молодого и таким образом создать парадокс. В более общем смысле, парадокс заключается в том, что люди или предметы могут путешествовать во времени и стать причиной событий, несовместимых с тем, что на самом деле произошло. (см. следующие работы: Гёдель, 1949; Ирман, 1972; Маламент, 1985 a и b; Хорвич, 1987).

Сильный аргумент против этого — это то, что, согласно логике, несовместимые события никак не могут произойти. Так что в действительности все подобные схемы, создающие парадокс, обречены на провал. Так в чем же причина беспокойства?

Первый вопрос, который беспокоит нас: почему такие схемы не работают? Не налагает ли необходимость несостоятельности таких схем на первый взгляд необычные и неожиданные ограничения на действия вещей или людей, которые перемещались во времени? Нет ли у нас основания принять, что таких ограничений не существует (в этом мире) и, следовательно, нет и путешествий во времени (в этом мире)? Мы позднее вернемся к вопросу о «вкусовых предпочтениях» при наложении таких ограничений, но прежде мы рассмотрим аргумент, что путешествия во времени не налагают никаких ограничений.

Топология и ограничения

Уилер и Фейнман (1949) были первыми, кто утверждал, что тот факт, что природа непрерывна во времени, является аргументом против того, что более поздние события, обусловливающие более ранние (что возможно в результате путешествий во времени), не приведут к появлению парадокса без необходимости в задании каких-либо ограничений. Модлин (1990) показал, как обобщить их довод и сделать его более точным, но утверждал, что тем не менее этот довод все-таки не обладал полностью общим характером.

Представьте следующие события. Вначале у нас есть фотокамера с черно-белой пленкой, и мы готовы сделать фотографию того, что бы не появилось из машины времени. Из машины появится предмет. В действительности этот предмет — это проявленная пленка. Мы фотографируем ее и проявляем пленку. Проявленную пленку затем кладут в машину времени и отправляют ее в то время, когда был сделан снимок. Мы определенно создадим парадокс: проявленная пленка будет иметь обращенные цвета — черный, белый и оттенки серого — того предмета, который выйдет из машины времени. Проявленные черно-белые пленки (т. е. негативы) имеют обращенные оттенки серого тех объектов, которые были засняты на них. Но поскольку предметом, который появляется из машины времени, является сама проявленная пленка, получится парадокс.

Однако нетрудно понять, что здесь никакого парадокса нет. Произойдет следующее: появится однородно серая картинка, а на проявленной пленке будет точно такой же однородный оттенок серого. Неважно, какова чувствительность пленки: пока яркость проявленной пленки зависит от яркости фотографируемого объекта непрерывным образом, всегда найдется оттенок серого, который при фотографировании даст точно такой же оттенок на проявленной пленке. В этом была суть идеи Уилера и Фейнмана. Давайте сначала рассмотрим проблему более точно, а затем — в более общем виде.

Для простоты предположим, что на пленке всегда запечатлен однородный оттенок серого (т. е. в любой момент времени оттенок серого не изменяется нигде на пленке). Возможные оттенки серого, появляющиеся на пленке, можно обозначить вещественными числами от 0 (полностью черный) до 1 (полностью белый).

Выделим теперь в хронологическом порядке различные стадии жизненного цикла пленки. На стадии S1 пленка неэкспонирована; ее только что зарядили в аппарат, и она готова для съемки. Затем на ней запечатлевают объект, появившийся из машины времени (на самом деле, этот объект — та же пленка на более поздней стадии своего жизненного цикла). В тот момент, когда мы подойдем к стадии S2 жизненного цикла пленки, она уже будет проявлена и готова к помещению в машину времени. Стадия S3 наступает сразу после того, как пленка появляется из машины времени, и как раз перед тем, как она будет сфотографирована. Стадия S4 наступает после того, как пленка была сфотографирована и до того, как она начинает терять цвет. Предположим, что пленка начинает свой жизненный цикл в состоянии S1, имея некий однородный оттенок серого, и что только значительная перемена оттенка серого происходит между стадиями S1 и S2. В этот период она приобретает оттенок серого, который зависит от оттенка серого сфотографированного объекта. Это означает, что оттенок серого, приобретенный пленкой на стадии S2, зависит от того оттенка серого, который она имела на стадии S3. Влияние оттенка серого, который пленка имеет на стадии S3, на оттенок серого, который пленка имеет на стадии S2, может быть представлено в качестве отображения («mapping») или функции, т .е. зависимости вещественных чисел от 0 до 1 (включительно) от других вещественных чисел от 0 до 1 (включительно). Предположим, что процесс фотографирования происходит таким образом, что если оттенок серого объекта изменяется гладко и непрерывно, то и оттенок серого, который имеет снимок объекта, будет также изменяться гладко и непрерывно. Из этого следует, что описываемая функция будет непрерывной. Итак, любая непрерывная функция зависимости вещественных чисел от 0 до 1 (включительно) от других вещественных чисел от 0 до 1 (включительно) должна включать хотя бы одно число. В этом можно быстро убедиться, построив графики таких функций. Можно легко увидеть, что любая непрерывная функция f от [0,1], значениями которой являются [0,1], должна в какой-либо точке пересекать прямую x=y, и поэтому должна быть хотя бы одна точка x, для которой f(x)=x. Такие точки называются неподвижными точками («fixed points») функции. Посмотрим теперь, чему может соответствовать такая неподвижная точка. Она соответствует оттенку серого, который, когда его сфотографируют, даст на проявленной пленке такой же оттенок. Наличие такой неподвижной точки означает, что явный парадокс разрешен.

Рассмотрим вопрос в более общем виде: допустим, что мы используем цветную фотографию. Каждый возможный цвет предмета (одного цвета) можно представить в качестве определенных соотношений синего, зеленого и красного, которые составляют один цвет. По тому же принципу телевизионные экраны дают все возможные цвета. Таким образом можно представить все возможные цвета предмета, отложив точки на трех координатных ортогональных осях x, y и z, поместив, по сути, точку в трехмерный куб. Такой куб также известен как прямое или Декартово произведение («Cartesian product») трех отрезков, отложенных на линиях. В данном случае можно также показать, что любой непрерывный график от куба до самой функции имеет хотя бы одну неподвижную точку. Следовательно, цветная фотография тоже не может быть использована для создания парадоксов путешествий во времени!

Давайте в более общем виде рассмотрим некую систему P, которая, как и в вышеприведенном примере, имеет следующий жизненный цикл. Система начинает в некотором состоянии S1, она взаимодействует с объектом, выходящим из машины времени (который является более поздним самим собой); система путешествует обратно во времени, взаимодействует с неким объектом (который является более ранним самим собой) и, в конце концов, система стареет и умирает. Предположим, что набор возможных состояний системы P может быть представлен как Декартово произведение n замкнутых интервалов вещественных чисел, т. е. предположим, что топология пространства состояний («state-space») P изоморфно конечному Декартову произведению замкнутых интервалов вещественных чисел. Далее предположим, что развитие P во времени и зависимость этого развития от состояния объектов, с которыми она взаимодействует, являются непрерывными. Тогда, согласно хорошо известной в топологии теоремы о неподвижной точке (см. Хокинг и Янг, 1961, с. 273), независимо от природы взаимодействия и независимо от начального состояния объекта, найдется хотя бы одно состояние S3 более старой системы (так как оно вызвано машиной времени), которое будет влиять на начальное состояние S1 более ранней системы (когда она возникнет рядом с более старой системы) таким образом, что когда система начнет стареть, она перейдет в состояние S3. Таким образом, без дополнительных ограничений, налагаемых на начальное состояние S1 системы P, мы показали, что всегда найдутся простые непарадоксальные решения, в которых все происходящее обусловлено обычными законами развертывания. Конечно, существует причинная циклическая обусловленность; следовательно, у нас есть такое же циклическое объяснение, но что можно ожидать, если временя тоже зациклено?

К сожалению, для любителя путешествий во времени, некоторое рассуждение предполагает, что существуют системы, для которых необходимая теорема о неподвижной точке не сохраняется. Представим, например, что у нас есть циферблат часов, который может вращаться лишь в одной плоскости. Мы собираемся положить циферблат в машину времени. Действительно, мы решили, что если мы увидим более позднее состояние циферблата, выходящего из машины времени, на угле x, мы переставим циферблат на x+90 и забросим его в машину времени. Теперь кажется, что мы пришли к парадоксу, поскольку отображение, состоящее из поворотов всех точек в круговом пространстве состояний на 90 градусов, не имеет неподвижной точки. И почему некоторые пространства состояний не будут иметь топологию круга?

Однако до настоящего времени мы не использовали другое предположение о непрерывности, которое также является обоснованным. До этого мы выдвинули только следующее требование: состояние, в котором циферблат находится на стадии S2, должно быть непрерывной функцией от состояния циферблата на стадии S3. Но состояние циферблата на стадии S2 достигается фиксированием состояния циферблата на стадии S1 и его поворотом на некоторый угол. Это явно не тот случай, когда эффект от взаимодействия, а именно состояние циферблата на стадии S2, должен быть непрерывной функцией причины, а именно состояния циферблата на стадии S3. Это к тому же тот случай, когда пройденный путь, т. е. то, каким образом циферблат вращается между состояниями S1 и S2, должен быть непрерывной функцией от состояния на стадии S3. И, что удивительно, оказывается, что это осуществить невозможно. Проиллюстрируем, в чем состоит проблема, перед тем, как перейдем к более общему рассмотрению того, что в случае с циферблатом должно в существовать решение, связанное с неподвижной точкой.

На время забудьте о путешествиях во времени. Предположим, что у вас и у меня есть часы с одним циферблатом. И ваши, и мои часы стоят. Стрелка моих часов стоит на 12. Вы собираетесь сказать, сколько показывают ваши часы. Моей задачей будет подстроить мои часы под ваши, в зависимости от того, что вы скажете. У моих действий при этом должна быть непрерывная зависимость (с одним значением) от времени, которое вы укажете. Удивительно, но это невозможно! Предположим, что вы скажете: «12». Тогда я устанавливаю это время, не предпринимая никаких действий. Теперь представим, что вы медленно и непрерывно называете каждый раз все более поздний час, начиная с 12. В силу непрерывности, я должен устанавливать каждое время, поворачивая свой циферблат против часовой стрелки. Если в какой-то момент я меняю тактику и достигаю поставленной цели путем вращения циферблата по часовой стрелке, то я внесу прерывистость в свои действия, т. е. в действия, которые я совершаю как функцию от названного угла. Таким образом, я буду вынужден, согласно непрерывности, выставлять каждое объявляемое значение путем вращения циферблата против часовой стрелки. Но такое вращение против часовой стрелки резко прервется, как только объявляемые числа, увеличиваясь, в конце концов снова придут к 12 часам, так как я выставляю 12 часов, совсем не поворачивая циферблат. Таким образом, возникнет разрыв непрерывности на 12 часах в заключительной точке. В принципе невозможно поддерживать непрерывность моих действий как функцию объявляемых величин на протяжении всего процесса, если я буду обязан воспроизвести все возможные значения. Для того, чтобы рассмотреть данную задачу иначе, можно рассуждать подобным образом: если мы начнем выставлять время с 12 часов, представляя, что мы выставляем каждый раз более раннее время, то мы будем вынуждены, в силу непрерывности, достигать объявленного значения времени, поворачивая циферблат по часовой стрелке. Но выводы, которые можно сделать из предположения о непрерывном увеличении значений и предположения о непрерывном уменьшении значений, не согласуются друг с другом. Таким образом, мы пришли к несогласованности, которая следует из непрерывности и предположения, что мне всегда удается подстроить время своих часов под время ваших часов. Следовательно, циферблат, изменяющий в соответствии с непрерывной динамикой свое состояние из заданного начального состояния, не может быть настроен согласно положению другого циферблата, с которым он взаимодействует, таким способом, чтобы гарантированно заканчивать поворотом на угол, выставленном на другом циферблате. Аналогично этому, первый циферблат не может быть настроен так, чтобы мы гарантированно заканчивали поворотом на 90 градусов по отношению ко второму циферблату. Все это не имеет никакого отношения к путешествиям во времени. Однако невозможность создания таких ситуаций является тем, что предотвращает поворот нами циферблата на 90 градусов, что создало бы парадокс при путешествии во времени.

Зададим положительный результат, который заключается в том, что с такими циферблатами всегда найдется решение с неподвижными точками, пока динамика непрерывна. Назовем состояние циферблата до взаимодействия с более поздней копией себя начальным состоянием циферблата. А то состояние, в котором находится циферблат на выходе из машины времени, мы назовем конечным. Обозначим возможное начальное и конечное состояния циферблата через углы x и y, на которые циферблат может быть выставлен в начале и в конце. Набор возможных начальных и конечных состояний образует тор (см. рис. 1).

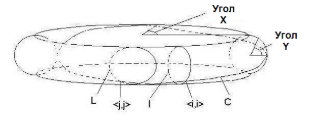
Предположим, что выставлен начальный угол I циферблата. Начальный угол I, на котором циферблат находится до того, как он возникнет рядом с более поздней копией самого себя, и набор всех возможных конечных углов, на которых циферблат может находиться при выходе из машины времени, представлены в виде круга I (см. рисунок 1). При любом возможном угле выходящего циферблата, циферблат, находящийся изначально на угле I, повернется на некоторый другой угол. Это изменение можно показать, повернув каждую точку в круге I в горизонтальном направлении на соответствующую величину. Поскольку вращение должно непрерывно зависеть от угла выходящего циферблата, кольцо I во время этой трансформации выродится в петлю L, лежащую на торе. Петля L соответствует углу x, на котором находится циферблат в момент помещения в машину времени, при условии, что он начал вращение на угле I и затем возник рядом с циферблатом (с более поздней копией самого себя), который находится на угле y при появлении из машины времени. Согласованность появляется, если x=y для некоторых x и y на петле L. Теперь пусть петля C будет петлей, состоящей из всех точек тора, для которых x=y. Кольцо I пересекает C в точке <i,i>. Очевидно, что любая непрерывная деформация круга I будет пересекать C в какой-либо точке. Таким образом, петля L должна пересекать C где-либо — допустим, в точке <j,j>. Но это означает, что не имеет значения, как вращение циферблата, начатое от угла I, зависит от угла появляющегося циферблата — для появляющегося циферблата найдется такой угол, при котором первый циферблат повернется именно на этот же угол (к тому времени, когда он войдет в машину времени) именно под влиянием появляющегося циферблата. Так что неважно, с какого угла начинать, и неважно, каким образом вращение циферблата зависит от угла появляющегося циферблата. Таким образом, даже для кругового пространства состояний нет необходимых ограничений (кроме непрерывности).

К сожалению, есть пространства состояний, обходящие даже эту необходимость. Рассмотрим, например, указатель, который может быть установлен на все значения от 0 до 1 (кроме самих значений 0 и 1). При этом предположим что у нам есть пространство состояний, изоморфное открытому множеству вещественных чисел. Теперь предположим, что у нас есть машина, которая устанавливает указатель на половину того значения, на котором он стоит при появлении из машины времени.

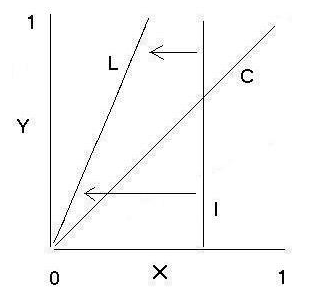
Рисунок 2

Предположим, указатель начинает с указания на значение I. Как и ранее, мы можем представить сочетание этого начального положения и всех возможных конечных положений с помощью линии I. Под влиянием указателя, выходящего из машины времени, значение указателя изменится так, что оно будет равно половине конечного значения указателя, выходящего из машины. Это изменение можно представить как непрерывное вырождение линии I в линию L, что показано стрелками на рисунке 2. Это изменение полностью непрерывно. Точки <x,y> на линии I обозначают начальное положение x=I (раннего во времени) указателя и положение y более позднего указателя в момент его появления из машины времени. Точки <x,y> на линии L обозначают положение x, в которое должен придти более ранний указатель, если он столкнется с более старым указателем, выходящем из машины времени и находящимся в положении y. Поскольку указатель устроен таким образом, что он должен перейти на половину того значения, которое он обнаружит, линия L соответствует x=1/2y. Согласованность возникает, если найдется такая точка, которая перейдет в другую точку при возникновении рядом с этой точкой. Поэтому согласованность возникает, если есть такая точка <x,y> на линии L, при которой x=y. Однако такой точки нет: линии L и C не пересекаются. Поэтому не существует согласованного решения, несмотря на тот факт, что динамика полностью непрерывна.

Конечно, если бы 0 был одним из возможных значений, то L и C пересекались бы в точке 0. Это странно и удивительно: добавление только одной точки ко множеству возможных значений количества создает в данном случае различие между парадоксом и его отсутствием. Это своего рода соблазн — добавить одну точку к пространству состояний, чтобы избежать проблем. После всего вышесказанного можно заметить, что определенно никакие измерения не могут подсказать, включает ли набор возможных значений данную конкретную точку или нет. К сожалению, могут существовать убедительные теоретические обоснования предположений того, что некоторая количественная величина имеет открытое пространство состояний: множество всех возможных скоростей массивных объектов в специальной теории относительности определенно является открытым, поскольку оно включает все возможные скорости, вплоть до скорости света, но исключая ее саму. Количественные величины, имеющие несвязанные возможные значения, также приводят к появлению контрпримеров по отношению к рассмотренным аргументам о неподвижных точках. И для нас не является очевидным, почему следует исключить такие возможности. Так что аргумент о том, что ограничения не нужны совсем, не является полностью общим.

Интересный вопрос состоит в следующем: для каких конкретных пространств состояний существуют неподвижные точки? Общий ответ нам неизвестен (см. дополнительную информацию у Кутаха, 2003).

Общая возможность путешествий во времени в рамках общей теории относительности

Тема путешествий во времени широко обсуждается в контексте общей теории относительности. Путешествие во времени может иметь место в общих релятивистских моделях, в которых имеются замкнутые времениподобные кривые (closed time-like curves), которые мы будем называть для краткости «ЗВК». Времениподобная кривая — это просто пространственно-временная траектория, при движении по которой невозможно достичь или превысить скорость света. Времениподобные кривые, таким образом, представляют собой возможные траектории движения простых объектов. Если бы существовали времениподобные кривые, которые были бы замкнуты (образовывали петлю), то, двигаясь по такой кривой, мы никогда бы не превысили скорость света и через определенное (соответствующее) время мы бы вернулись в уже пройденную точку. Или, находясь близко к ЗВК, мы бы могли подойти произвольно близко к точке пространственного-временного континуума, в которой мы уже побывали. Общая теория относительности напрямую допускает путешествие во времени: оказывается, что существует много пространственно-временных континуумов с ЗВК, согласующихся с фундаментальными уравнениями общей теории относительности. Пространственно-временной континуум может везде иметь метрику Минковского и в то же время иметь ЗВК посредством топологически свернутого в окружность временного измерения. Или могут существовать соединения в виде «кротовых нор» («червоточин») между различными частями пространственно-временного континуума, позволяющие войти объекту в «отверстие A» такой норы, пройти через нее, выйти из нее через «отверстие B» и снова войти в «отверстие A». Или же могут существовать пространственно-временные континуумы, топологически обозначаемые R4, которые также имеют ЗВК в силу «отклонения» световых конусов (пространственно-временные континуумы Гёделя, Тауба-НУТ и т. д.).

Таким образом, благодаря общей теории относительности открывается множество возможностей для путешествий во времени. Заметьте, что даже если в континууме существуют ЗВК, это не означает, что можно добраться от одной точки континуума до другой по какой-либо времениподобной кривой, направленной в будущее. Во многих континуумах с ЗВК такие ЗВК существуют не во всем пространственно-временном континууме. Некоторые части пространственно-временного континуума могут иметь ЗВК, в то время как другие части могут и не иметь ЗВК. Назовем ту часть континуума, где есть ЗВК, областью путешествий во времени, а остальную часть — нормальной областью. Более точно, область путешествий во времени состоит из таких точек континуума p, при которых всегда найдется времениподобная кривая ненулевой длины, начинающаяся в p и возвращающаяся в p. Теперь мы начнем более детально тестировать пространственно-временные континуумы, содержащие ЗВК, на предмет возможных проблем.

Две игрушечные модели

Чтобы лучше понять весь смысл замкнутых времениподобных кривых (ЗВК), было бы полезно рассмотреть две простые модели. В континуумах с ЗВК традиционная проблема начального значения не может быть сформулирована обычным образом. Для этого необходимо существование поверхностей Коши; если ЗВК существуют, то поверхности Коши не существуют (поверхность Коши — это такая пространственноподобная поверхность, которую каждая нерастяжимая времениподобная пересекает только один раз; обычно начальные условия задаются условиями для такой поверхности). Тем не менее, если топологические сложности многообразия локализованы подходящим образом, то мы можем подойти к проблеме совсем близко. Назовем неограниченную пространственноподобную поверхность S квазиповерхностью Коши («quasi-Cauchy surface») при условии ее разделения остальной части многообразия на две части так, чтобы а) каждая точка многообразия могла быть соединена с S посредством времениподобной кривой и б) любая времениподобная кривая, которая соединяет точку в одной области с точкой в другой области, пересекала S только один раз. Очевидно, что квазиповерхность Коши должна полностью заселить нормальную область пространственно-временного континуума; если любая точка p, принадлежащая S, будет находится в области путешествий во времени, то любая времениподобная кривая, которая проходит через p, может быть продолжена до времениподобной кривой, которая снова пересекает S вблизи p. В исключительных случаях путешествий во времени данная модель может вообще не иметь нормальной области (например, пространственно-временной континуум Минковского, свернутый в цилиндр во времениподобном направлении), в которой наши обычные понятия о предшествовании во времени будут неприменимы. Но временные аномалии, такие как кротовые норы (и машины времени) могут быть достаточно локализованными, чтобы допустить существование квазиповерхностей Коши.

Будучи расположенной во времениподобной ориентации, квазиповерхность Коши без проблем делит многообразие на его прошлое (т. е. на все точки, которые могут быть достигнуты, если мы будем перемещаться по кривой, направленной в прошлое из S) и будущее (с необходимыми изменениями). Если прошлое S полностью находится в нормальной области пространства, то S является частичной поверхностью Коши: каждая нерастяжимая времениподобная кривая, существующая в прошлом S, пересекает S строго один раз, но (если существуют путешествия в будущее) не каждая нерастяжимая времениподобная кривая, существующая в будущем S, пересекает S. Теперь мы можем рассмотреть следующую четко определяемую проблему. Давайте рассмотрим многообразие, содержащее область путешествий во времени и имеющее также такую частичную поверхность Коши S, при которой все временные «странности» относятся к будущему S. Если все, что мы могли бы видеть, было бы поверхностью S и ее прошлым, мы бы не узнали, что в континууме вообще существуют путешествия во времени. Вопрос в следующем: есть ли какие-либо ограничения, налагаемые на данные, которые могут быть нанесены на S и доведены до глобального решения, которые отличны от ограничений (если таковые существуют), налагаемых на данные, которые могут быть нанесены на поверхность Коши в односвязном пространстве и доведены до глобального решения? Если существует путешествие в будущее, то сможем ли мы сказать об этом в настоящий момент из-за предполагаемой странности в пространственной конфигурации настоящего?

Нет ничего удивительного в том, что могут возникать ограничения для данных, которые могут быть нанесены на пространственноподобную поверхность, проходящую через область путешествий во времени: в конце концов, мы никогда не сможем беспрепятственно определить, что происходит на пространственноподобной поверхности и на другой такой же поверхности в ее будущем, но в этом случае поверхность, о которой мы говорим, находится в своем будущем. Но если бы накладывались отдельные ограничения для данных на частичной поверхности Коши, то нам бы очевидно потребовалось бы исключить некоторые виды состояний, приемлемые в противном случае для S, в том случае, если существуют путешествия в будущее по поверхности S. Тогда бы мы смогли установить, что путешествий в будущем не будет через простое наблюдение текущего состояния Вселенной. Как мы увидим, есть основание подозревать, что такие ограничения, налагаемые на частичную поверхность Коши, не являются общими. Но мы заходим далеко вперед: давайте сначала рассмотрим эффект путешествия во времени на очень простой динамической модели.

Простейший возможный пример — это ньютоновская теория идеально упругих соударений макрочастиц в одном пространственном измерении. Пространственно-временной континуум является двумерным, так что мы можем вначале представить его в виде Евклидовой плоскости. Динамика частиц полностью задана двумя условиями. Когда частицы перемещаются свободно, их траектории (или «мировые линии») — это прямые линии, а когда две частицы сталкиваются, они обмениваются импульсами таким образом, что столкновение в континууме выглядит как ‘X’, при этом каждая частица меняет свой импульс при ударе.[1] Динамика частиц полностью локальна, и в ее рамках можно убедиться, что множество мировых линий составляет модель динамики, т. е. законы динамики выполняются в каждой небольшой произвольной области. Также тривиальным является нахождение решений, отталкиваясь от произвольных начальных данных, если не существует ЗВК: имея начальные координаты и импульсы нескольких частиц, можно просто провести прямую линию от каждой частицы в подходящем направлении и бесконечно продолжать ее. Как только будут построены все линии, мировая линия каждой частицы может быть проведена от соударения к соударению. Граничная задача (boundary-value problem) для такой динамики обозначена довольно четко: любой массив данных в любой момент времени выдает единственное глобальное решение, полученное вышеописанным методом.

Что произойдет, если мы вручную изменим топологию континуума таким образом, чтобы появились ЗВК? Наиболее простой способ сделать это показан на рис. 3: мы как бы редактируем континуум с помощью компьютерных команд «вырезать» и «вставить» таким образом, что он оказывается разделенным линиями L− и L+. Частицы, входящие в L+ снизу, появляются из L−, а частицы, входящие в L− снизу, появляются из L+.

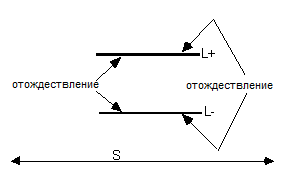
 Рисунок 3. Вставка ЗВК с помощью компьютерных команд «вырезать» и «вставить»

Как изменилась граничная задача после такой модификации пространственно-временного континуума? До «удаления» и «вставки» мы можем ввести произвольные данные в срез одновременности S и довести их до единственного решения. S больше не является поверхностью Коши после изменения топологии, поскольку ЗВК никогда не пересечет ее, — это теперь частичная поверхность Коши. Теперь мы можем задать два вопроса. Первый: могут ли произвольные данные, нанесенные на S, всегда быть доведены до глобального решения? Второй: является ли это решение единственным? Если ответ на первый вопрос — «нет», то возникает обратно-временное ограничение: существование области с ЗВК налагает ограничения на события, происходящие на S, даже если эта область полностью находится в будущем поверхности S. Если ответ на второй вопрос — «нет», то мы придем к индетерминизму в его странном проявлении: полное физическое состояние S не определяет физического состояния в будущем, хотя локальная динамика является полностью детерминистской и нет никакого другого ограничения для области континуума, соответствующей будущему для S (т. е. граничным значениям, которые могли бы оказывать влияние на состояние области, неоткуда взяться).

В таком случае ответ на первый вопрос — «да», а на второй — «нет»: нет ограничений для данных, наносимых на S, но эти данные всегда согласуются с бесконечностью различных глобальных решений. Простой способ понять, что всегда существует решение, заключается в построении минимального решения следующим образом. Начнем с проведения прямых линий, исходящих из S, как этого требуют исходные данные. Если линия придет в L− снизу, то продолжим ее как выходящую из L+ сверху в соответствующем месте, а если линия придет в L+ снизу, то продолжим ее как исходящую из L− в соответствующем месте. На рис. 4 показано минимальное решение для отдельной частицы, которая входит в область путешествий во времени с левой стороны.

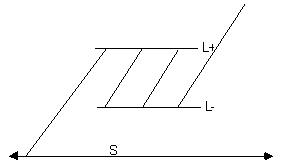
Рисунок 4. Минимальное решение

Частица «перемещается назад во времени» три раза. Очевидно, что это минимальное решение является глобальным решением, поскольку частица всегда движется равномерно.

Но то же самое начальное состояние на S также согласуется с другими глобальными решениями. Новое требование, задаваемое топологией, заключается лишь в том, что данные, входящие в L+ снизу, должны соответствовать данным, выходящим из L− сверху, а данные, входящие в L− снизу, должны соответствовать данным, исходящим сверху из L+. Таким образом, мы можем добавить любое число вертикальных линий, соединяющих L- и L+, и все так же получать решение. Например, добавление нескольких таких линий к минимальному решению приводит к следующему:

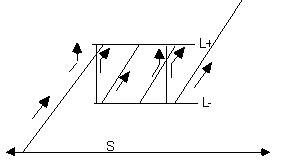
Рисунок 5. Неминимальное решение

Теперь частица сталкивается с самой собой дважды: сначала перед тем, как она достигнет L+ в первый раз, а затем незадолго до того, как она выйдет из области ЗВК. С точки зрения частицы, она движется вправо с постоянной скоростью до тех пор, пока она не ударит более старую копию самой себя и не перейдет в состояние покоя. Она находится в состоянии покоя до тех пор, пока ее не ударит справа более ранняя копия ее самой, и тогда частица продолжит движение. Тот же самый процесс повторяется позже. Понятно, что это глобальная модель динамики и что любое количество различных моделей может быть построено путем изменения числа и расположения вертикальных линий.

Данные об S в таком случае дают нам лишь неполную информацию о том, что происходит с частицей. Мы знаем, что частица войдет в область ЗВК и достигнет L+, мы знаем, что она будет единственной частицей во Вселенной, и мы точно знаем, в каком направлении и с какой скоростью она покинет область ЗВК. Но мы не можем определить, ни сколько столкновений произойдет с частицей (если таковые возможны), ни как долго она задержится (на соответствующее время) в области ЗВК. Если бы частица была часами, мы бы не могли предсказать, какое время бы она бы показывала, покидая эту область. Более того, динамика не дает нам никакого средства определения различных возможностей: нет вероятностей, привязанных к каждому возможному исходу процесса.

Изменение топологии изменило математическое описание двумя диаметрально противоположными способами. С одной стороны S больше не является поверхностью Коши, так что, вероятно, неудивительно, что данных об S недостаточно для нахождения единственного глобального решения. Но с другой стороны существует дополнительное ограничение: данные, выходящие из L− должны в точности соответствовать данным, входящим в L+, даже если то, что выходит из L− помогает определить то, что входит в L+. Это добавочное ограничение согласованности обладает тенденцией к сокращению числа решений, хотя в данном случае дополнительное ограничение является более чем несущественным благодаря существованию различных видов данных на L+/L-.

Факт существования различных данных, перевешивающий дополнительное ограничение, также указывает на неожиданный способ, с помощью которого могут быть разрешены парадоксы путешествий во времени. Попробуем создать парадоксальную ситуацию, используя небольшую замкнутую петлю времени, описанную выше. Если мы с левой стороны направим отдельную частицу внутрь петли, не сделав ничего другого, то мы будем точно знать, в каком месте она покинет правую сторону области путешествий во времени. Теперь предположим, что мы ставим кого-либо с другой стороны области и даем ему следующее задание: если частица вылетела с правой стороны, то человек должен сделать что-либо, чтобы не допустить попадания частицы на левую сторону в месте вхождения в петлю. На самом деле это довольно просто: если мы направляем частицу с правой стороны, то нам кажется, что она может вылететь с левой стороны и отклонить частицу, влетающую с левой стороны.

Продолжая наше рассуждение подобным образом, мы далее увидим, что если частица вылетит справа, то мы сможем просто отправить ее назад, чтобы отклонить ее саму от места вхождения. Следовательно, все, что нам нужно сделать — это поставить зеркало, идеально отражающее частицы, справа от области путешествий во времени и запустить частицу с левой стороны так, чтобы она слегка задела L+ (если ничего не препятствует этому). Теперь наш парадокс полностью описан. С одной стороны, если ничто не препятствует частице, то она войдет в область путешествий во времени с левой стороны, выйдет с правой, будет отражена зеркалом, снова войдет справа и выйдет слева, что исключает попадание частицы в область путешествий в дальнейшем. Следовательно, если частица вошла в область, то она отражается и больше никогда не входит снова. С другой стороны, если частица никогда не войдет в петлю, то слева ничего не произойдет, ничего не выйдет справа, ничего не будет отражено и ничто не отклонит частицу от попадания в область путешествий. Таким образом, если она не входит, то ее нечем отразить — и она входит. Если она входит, то она отклоняется и не входит; если она не входит, то нечем отразить ее и она входит. В этом и заключается парадокс.

Но в то же время легко получить по крайней мере одно решение предложенного парадокса: следуйте только указаниям по построению минимального решения, продолжая изначальную траекторию частицы (зеркало отражает ее очевидным образом), а затем возьмите числа и траектории частиц с результирующих диаграмм. Результат показан на рис. 6.

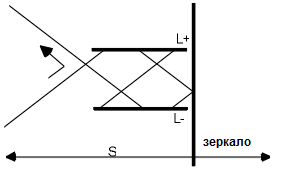
Как мы можем видеть, частица, приближающаяся с левой стороны, никогда не достигнет L+: ее до этого отклоняет частица, появляющаяся из L-. Но она не отклоняется самой собой, как предполагает данный парадокс, а ее отклоняет другая частица. На самом деле теперь на диаграмме существуют четыре частицы: исходная частица и три частицы, заключенные в замкнутые времениподобные кривые. Это не крайняя левая частица, отражаемая зеркалом, и даже не та частица, которая отклоняет крайнюю левую частицу, — это, вообще, другая частица.

Парадокс проистекает из некорректной предварительной формулировки: если в мире на поверхности S существует только одна частица, то найдется только одна частица, которая может участвовать во взаимодействии в области путешествий во времени; отдельная частица должна будет взаимодействовать с более ранней (или более поздней) копией самой себя. Но мы не знаем, что может выйти из L−, при этом существует единственное требование: все, что появляется, должно соответствовать тому, что входит на L+. Таким образом, если вы решили заняться созданием работоспособной машины времени, то вы должны быть готовы испытать еще одно разочарование: когда вы попробуете переместится в прошлое, чтобы убить себя, вас, возможно, остановит непредвиденный субъект, который появится из машины, т. е. вы не сможете войти в машину времени. И тогда вы снова столкнетесь с особым случаем индетерминизма: если существует много самосогласованных вещей, которые могут не позволить вам войти в машину, то у вас вообще нет никакой информации о том, какая из них вероятнее всего сможет при этом материализоваться.

Когда некоторая свобода в нанесении данных на L− сделает так, что ограничение, заключающаяся в том, что те же самые данные должны переходить в L+, станет незначительным, вместо парадокса мы получим ошеломляющее богатство выбора, т. е. множество решений, согласующихся с данными на S. Чтобы найти случай, в котором ограничение становится более существенным фактором, чем свобода, нам нужно построить особую искусственную динамику и топологию. Рассмотрим пространство всех линейных динамик для скалярного поля на решетке. Можно представить решетку как простой дискретный пространственно-временной континуум. Мы построим пространственно-временную решетку как ориентированный граф («directed graph»). Должно существовать скалярное поле, определенное в каждой вершине графа, значения которого в данной вершине зависят линейно от значений поля в вершинах, имеющих стрелки, приводящие к этим значениям. Для каждого ребра графа можно использовать весовой коэффициент, который определяет вклад поля в вершине ввода в поле в вершине вывода. Если мы обозначим вершины буквами латинского алфавита a, b, c, ..., а ребра обозначим очевидным образом их конечными точками, то мы сможем обозначить весовые коэффициенты теми ребрами, с которыми они связаны, с той же очевидностью.

Предположим, что граф пространственно-временной решетки является ациклическим (см рис. 7). Граф является ациклическим, если отсутствует возможность перемещения в направлении стрелок по петле.

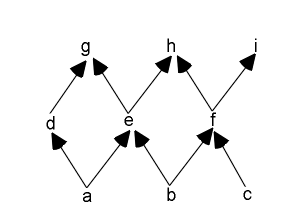
Несложно рассматривать набор вершин в качестве аналога поверхности Коши (например, набор {a, b, c}), и очевидно, что если произвольные данные будут нанесены на эти вершины, то эти данные приведут в будущем к единственному решению.[2] Если значение поля в вершине a равно 3, а в вершине b равно 7, то его значение в вершине d будет равно 3Wad, а в вершине e — 3Wae + 7Wbe. Изменяя весовые коэффициенты, мы можем управлять динамикой, но в ациклическом графе эволюция поля в будущем всегда будет единственной в своем роде.

Теперь давайте снова искусственно поменяем топологию решетки, чтобы допустить существование ЗВК и сделать так, чтобы граф стал замкнутым. Один из простейших таких графов показан на рис. 8. Теперь существуют пути, которые приводят от z к нему же, например, от z к y, а затем от y к z.

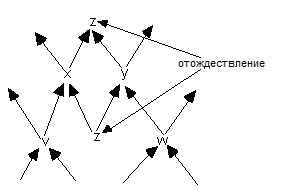
Можем ли мы ввести произвольные данные в v и w и довести эти данные до глобального решения? Будет ли решение единственным?

В общем случае найдется решение, и это решение будет единственным. Уравнения значения поля при x, y, и z имеют вид:

x = vWvx + zWzx 

y = wWwy + zWzy 

z = xWxz + yWyz. 

Решение этих уравнений для z дает:

z = (vWvx + zWzx)Wxz + (wWwy + zWzy)Wyz 

или

z = (vWvxWxz + wWwyWyz)/ (1 − WzxWxz − WzyWyz),

которое дает единственное значение z в общем случае. Но если рассмотреть пространство всех возможных видов динамики решетки (т. е. пространство всех возможных весовых коэффициентов), то мы придем к сингулярности для 1−WzxWxz − WzyWyz = 0. Если мы выберем весовые коэффициенты именно таким образом, то произвольные данные v и w не смогут быть доведены до глобального решения. В самом деле, если скалярное поле во всех точках неотрицательно, то данный конкретный выбор динамики налагает жесткие ограничения на поле в точках v и w: в этих точках поле должно быть равно нулю (при том, что Wvx и Wwy должны иметь ненулевые значения); также во всех вершинах в их прошлом значение поля должно быть равно нулю. Если поле может принимать отрицательные значения, то v и w должны быть подобраны таким образом, что vWvxWxz = −wWwyWyz. В любом случае значения поля в точках v и w строго ограничены существованием области ЗВК, даже если эти вершины полностью находятся в прошлом этой области. Это ограничение не похоже на все то, что существует в рамках классической физики.

Наши игрушечные модели имеют три характерные черты. Первая заключается в том, что может оказаться невозможным доказать полностью в общем виде: произвольные данные на частичной поверхности Коши всегда могут быть доведены до глобального решения, и наш искусственно созданный случай включает пример, в рамках которого это невозможно. Вторая — в том, что такие странные ограничения, вероятно, не являются общими: чтобы получить проблему, мы должны провести «тонкую настройку» рассматриваемой динамики. Третья характерная черта — в том, что противоположная проблема, а именно данные на частичной поверхности Коши, согласующиеся со многими различными глобальными решениями, являются, вероятно, общими: для получения результата здесь не требуется никакой «тонкой настройки». И это приводит к особому виду индетерминизма: общее состояние для S не определяет то, что произойдет в будущем, даже если локальная динамика является детерминистской и если не существует никаких «краев», ограничивающих пространственно-временной континуум, данные из которого могут влиять на конечный результат. То, что происходит в области путешествий во времени, ограничено, но не детерминировано тем, что происходит на S, и динамика не предоставляет даже никаких вероятностей для различных возможностей. Пример с фотонегативом, который мы обсуждали в разделе 3, теперь представляется, скорее всего, необычным, т. к. в данном случае существует единственная неподвижная точка в его динамике, а условия в сочетании с динамическими законами определяют конечный результат. В общем случае скорее можно ожидать реализацию нескольких неподвижных точек, на которые даже вероятностно ничего не оказывает влияния.

В этом есть некая ирония: в общем виде путешествия во времени должны приводить не к противоречиям или ограничениям (в нормальной области), а к недоопределенности («underdetermination») того, что происходит в области путешествий во времени посредством того, что происходит во всех остальных областях (недоопределенность не связана ни с вероятностной динамикой, ни со свободным краем пространственно-временного континуума). Традиционное аргумент против путешествий во времени заключается в том, что не существует согласованного способа закончить произвольно построенную историю о том, как должно происходить такое путешествие с точки зрения путешественника. Вместо этого оказывается, что проблема заключается в недоопределенности: история может быть согласованно закончена многими различными способами.

Замечания и ограничения для игрушечных моделей

Две игрушечные модели, представленные выше, могут быть истолкованы математически, но они предполагают некоторые упрощения, т. е. при попытке усложнить эти модели могут возникать потенциальные проблемы. Преодолевая эти затруднения, мы сможем обозначить условия, которыми мы воспользовались.

Рассмотрим небольшую модификацию первой простой модели, которую нам предложил Адам Элга. Пусть частицы имеют электрический заряд, в результате которых возникают силы в соответствии с законом Кулона. Создадим ситуацию, представленную на рис. 9.

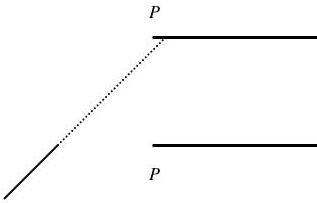
Рисунок 9. Схема парадокса Элга

Пунктирная линия показывает путь, который пройдет частица, если на нее не действует никакая сила. Точка, обозначенная P — это левый край области путешествий во времени; две отметки напоминают, что точка внизу и точка вверху представляют собой одно и то же.

Парадокс Элга состоит в следующем: если никакая сила не действует на частицу, то она попадет в область путешествий во времени. Но если она попадет в область путешествий во времени и, как следствие, появится снова, двигаясь вдоль нижнего края, то более старшая копия частицы после взаимодействия с собой более ранней отклонится от области путешествий во времени. Просто воссоздать этот случай можно легко: нужно сделать так, чтобы отклонение было бы достаточно сильным, чтобы частица не вошла в область путешествий даже в начальный момент. Например, пусть импульс частицы, входящей в область путешествий, будет очень мал. Явное существование одноименно заряженных частиц внутри области путешествий во времени будет достаточным, чтобы отклонить входящую частицу так, что она никогда не достигнет L+. Но если частица вообще никогда не войдет в данную область, то она никогда не отклонит саму себя...

Может возникнуть подозрение, что сложное скопление заряженных частиц в области путешествий во времени может очень помочь нам, как и в случае с вышеописанной проблемой зеркального отражения. Исключая случай, когда таких частиц бесконечно много, это не будет работать, как диктуют законы сохранения числа частиц и линейного импульса. Предположим, что некоторое конечное скопление частиц появляется из L- и создает отталкивающее электрическое поле, необходимое для отклонения входящей частицы. Тогда точно такое же скопление частиц должно быть «поглощено» на L+. Таким образом, во все моменты времени после L+ единственная частица во всем мире — это входящая частица, которая в настоящий момент была отклонена от своей изначальной траектории.

При этом отклонение означает, что линейный импульс частицы изменился по сравнению тем, каким он был до L-. Но это невозможно в силу закона сохранения импульса. Неважно, как исходящая частица взаимодействует с частицей в области путешествий во времени или как эти частицы взаимодействуют между собой — суммарный импульс всегда сохраняется при взаимодействии. И какой бы ни был линейный импульс у частиц, перемещающихся во времени, когда они появляются из L-, линейный момент будет большей частью поглощен на L+. Итак, импульс входящей частицы не может быть изменен через взаимодействие: частица не могла быть отклонена (к настоящему времени). Можно представить попытку построения кривой вида «S» в траектории входящей частицы, которая сначала отклоняется влево, а затем вправо, что сохраняет ее конечный импульс, который остается равным начальному, и наконец перемещается в пространстве, пролетая мимо L+. Но если в конце на частицу действует сила отталкивания, то снова вправо частица не может быть отклонена. В вышеописанном примере с зеркалом путь входящей частицы может быть изменен, не нарушая закона сохранения импульса, потому что в конце процесса импульс передается зеркалу.

Каким же образом пример Элга не подвергается нашему анализу? Почему принцип непрерывности не может гарантировать здесь наличие решения?

Предположение о непрерывности оказывается несостоятельным из-за двух особенностей данного примера: концентрация электрического заряда на точечной частице и то, как мы рассмотрели (или, точнее, не смогли рассмотреть) точку P, край L+ (и L-). Мы предположили, что точечная частица соударяется с L+ и затем появляется из L- или, в противном случае, не попадает в L+ и продолжает движение внутрь пространственно-временного континуума над ней. Это значит, что для заряда на входящей частице существует две возможности: или он будет полностью перенесен через время, или полностью избежит перемещения во времени. Посмотрим теперь, как изменится ситуация при равномерном распределении заряда.

Предположим, что, вместо того чтобы быть сконцентрированным в точке, входящий объект представляет собой небольшой прут с распределенным по нему электрическим зарядом (см. рис. 10).

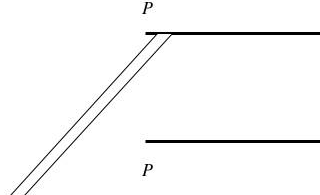
Рисунок 10. Парадокс Элга с заряженным прутом

И опять мы организуем все таким образом, что если на прут не действуют силы, то он будет полностью поглощен L+. Но теперь мы постулируем, что если прут все же попадет в точку P, то он сломается: часть его (которая ударится с L+) отправится назад во времени, а оставшаяся часть продолжит движение над L+. Таким образом, непрерывность восстановлена: у нас есть не только возможность отправить назад во времени весь заряд (или вообще не отправлять его), а у нас есть также различные промежуточные величины заряда для этой возможности.

Нетрудно увидеть, что восстановление непрерывности восстанавливает существование согласованного решения. Если заряд не отправлен назад во времени, то прут не отклонен и он целиком соударяется с L+ (и, как следствие, отправляется назад во времени). Если весь заряд отправляется назад во времени, то входящий прут отклоняется настолько, что он полностью обходит L+ и заряд назад во времени не отправляется. Но если соответствующее количество заряда пройдет в прошлое сквозь время, то прут будет отклонен лишь частично таким образом, что он попадет в краевую точку P и будет разбит на части, одна из которых переместится немного назад во времени, а другая этого не сделает, и та часть, которая переместится немного назад, будет иметь тот заряд, который необходим для того, чтобы вызвать необходимое отклонение (см. рис. 11).

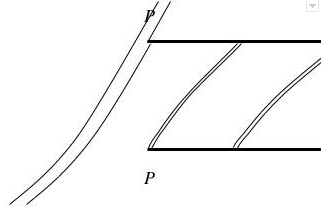
Рисунок 11. Разрешение парадокса Элга с заряженным прутом

Наша проблема сохранения импульса теперь также решена: часть прута, которая не перемещается во времени, в конце обладает более низким импульсом, чем прежде, а часть, перемещавшаяся во времени — более высокий (из-за Кулоновских сил), т. е. баланс будет достигнут.

Является ли обманчивым моделирование заряженной частицы в виде прута, распадающегося на части? Что, если мы будем настаивать на том, что частица является именно точечной частицей, и, следовательно, ее путешествие во времени происходит по принципу «все или ничего»?

В этом случае существует причина для беспокойства, так как с таким мы еще не сталкивались: что произойдет, если наша точечная частица будет находиться строго в точке P на диаграмме? Путешествует ли она во времени или нет? При рассмотрении этого вопроса мы должны рассмотреть особенность наиболее простого способа, с помощью которого мы осуществляли путешествия во времени в рамках наших игрушечных моделей при помощи компьютерных команд «вырезать» и «вставить». Наша повторная разметка структуры пространственно-временного континуума внесла довольно строгое ограничение: результирующий континуум больше не является многомерным, т. к. топологическая структура в точке P отлична от топологической структуры во всех остальных точках. Исследователи, занимающиеся математической физикой, просто-напросто не работают с такими структурами — обычно они просто удаляют «точку-нарушителя» из пространственно-временного континуума и восстанавливают таким образом многомерность. В этом случае в точке P может возникнуть голая сингулярность («bare singularity») — край, открытый в континуум, в котором может исчезнуть и из которого может появиться все, что угодно, любые физические объекты.

В частности, если мы будем настаивать, что наша частица является точечной, то при пересечении P ее траекторией, частица просто исчезнет. Что приведет к чрезвычайно удачному результату, при котором траектория точно попадет в P? Появление некоторых других заряженных частиц с необходимым зарядом и траекторией от P (на L-). И мы уже больше не связаны никакими законами сохранения: голая сингулярность позволяет как «проглатывать», так и «выдавать» частицы с любыми нужными нам массой, зарядом и импульсом. Следовательно, если мы будем настаивать на том, что частицы — точечные, то необходимо принимать во внимание сингулярность, что снова оказывает нам неоценимую помощь.

Рассмотрение этих (чуть более усложненных) игрушечных моделей, само собой, не отменяет необходимости доказательства теорем. Но эти модели определенно помогают проиллюстрировать разного рода соображения, которые становятся уместными тогда, когда мы подробно начинаем рассматривать физические законы при путешествиях во времени. Обсудим теперь некоторые результаты, относящиеся к некоторым несколько более реалистичным моделям, которые обсуждаются в литературе по физике.

Немного более реалистичные модели путешествий во времени

Эчеверрия, Клинхаммер и Торн в 1991 году рассматривали следующую модель: трехмерный одиночный жесткий шар, который проходит через одну кротовую нору и сталкивается со своей более ранней копией.

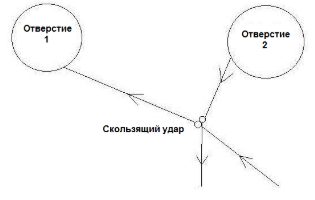
Угроза парадокса в этом случае проявляется следующим образом. Для шара существуют такие начальные траектории (начинающиеся в области, в которой путешествия во времени невозможны), что если такие траектории будут продолжены (в область путешествий во времени) при условии отсутствия столкновения шара перед попаданием в отверстие 1 норы, то он выйдет из отверстия 2 и столкнется со своей более ранней копией до попадания в отверстие 1, предотвращая тем самым попадание своей более ранней копии в отверстие 1. Поэтому кажется, что шар войдет в отверстие 1 тогда и только тогда, когда он в отверстие 1 не войдет. Стратегия Уилера-Фейнмана заключается в поиске решения по принципу скользящего удара («glancing blow»): столкновение, которое приведет к необходимому (малому) отклонению в траектории более ранней копии шара, которое вызовет именно это столкновение. Существуют ли всегда такие решения?[3]

Эчеверрия, Клинхаммер и Торн обнаружили огромное семейство начальных траекторий, имеющих согласованные непрерывности по типу скользящего удара и не нашли траекторий без непрерывностей (но их поиск не был до конца общим). Они не дали строгого доказательства, что каждая начальная траектория имеет согласованную непрерывность, но предположили, что наличие согласованной непрерывности у каждой начальной траектории является правдоподобным. Иными словами, правдоподобным с их точки зрения является то, что в случае бильярдного шара и кротовой норы структура путешествий во времени в пространственно-временном континууме, включающем такие норы, не приводит к ограничениям состояний на пространственноподобных поверхностях в области без путешествий во времени.

Действительно, как можно было бы ожидать после нашего обсуждения в предыдущем разделе, они вывели противоположную проблему из проблемы несогласованности: они обнаружили недоопределенность. Для большого семейства начальных траекторий существует много различных согласованных продолжений развития событий по типу скользящего удара (при этом многие траектории имеют между собой множественные кротовые норы). Например, если изначально имеется шар, который перемещается по траектории, направленной прямо между двумя входами в норы, очевидное решение заключается в том, что шар проходит от одного отверстия к другому без перемещений во времени. Но другое решение заключается в том, что более ранний шар оказывается «забит» в отверстие 1 специально, чтобы выйти из отверстия 2 и произвести это столкновение. Эчеверрия, Клинхаммер и Торн не отмечают возможности существования добавочных шаров в области путешествий во времени (на эту возможность мы указали в предыдущем разделе). Мы догадываемся (но не имеем доказательства) о том, что для каждой начальной траектории A существует в общем виде много вариантов дальнейшего развития событий.

Эчеверрия, Клинхаммер и Торн в 1990 году изучали случай с несамовзаимодействующими скалярными полями без источников, перемещающимися во времени через такую кротовую нору, и нашли, что наличие таких нор не налагает никаких ограничений на область без путешествий во времени. В принципе не существует известных контрпримеров по отношению к утверждению о том, что в «довольно реалистичных» пространственно-временных континуумах с перемещениями во времени с частичной поверхностью Коши не существует ограничений, налагаемых на состояние такой поверхности Коши посредством существования ЗВК (см. Фридман и Моррис, 1991, Торн, 1994 и Ирмэн, 1995; в разделе «Другие интернет-ресурсы» см. Ирмэн, Сминк и Вютрих, 2003).

Как насчет ограничений в области путешествий во времени T? На первый взгляд, существование ограничений в такой области не удивило бы нас. Но можно все еще ожидать, что не будет никаких ограничений на состояния на пространственноподобной поверхности, если поверхность «достаточно мала». В литературе по физике ставится следующий вопрос: для любой точки p в T и для пространственноподобной поверхности S, включающей p, найдется ли такая окрестность E точки p в S, что любое решение в E можно было бы распространить на весь пространственно-временной континуум? В соответствии с этим вопросом, существует несколько простых моделей, в рамках которых локальные решения могут быть расширены до глобальных, и несколько простых моделей, не обладающих такой расширяемостью, без явного общего образца. Технические математические проблемы дополнены более концептуальной проблемой того, что может произойти в ситуации, предполагающей построение замкнутых времениподобных кривых (см. Юртсевер, 1990; Фридман и соавторы, 1990; Новиков, 1992; Ирмэн, 1995; Ирмэн, Сминк и Вютрих, 2009; в разделе «Другие интернет-ресурсы» см. Ирмэн, Сминк и Вютрих, 2003). Что обо всем этом думать?

Ограничения. Ну и что?

Поскольку возможность избавления от ограничений в реалистичной модели не является очевидной, проверим аргумент о неправдоподобности путешествий во времени и о маловероятном их существовании в нашем мире, поскольку в мире существуют ограничения. Аргумент выглядит примерно следующим образом. Для того, чтобы не противоречить таким ограничениям, необходимо существование предопределенной «божественной гармонии» между глобальной структурой пространственно-временного континуума (перемещения во времени) и распределением частиц и полей на пространственноподобных поверхностях в нем. Но построение с «божественной гармонией», как частью единого плана, неправдоподобно для настоящего мира или любого другого мира, удаленно подобному нашему. На самом деле, с этим можно поспорить: у нас есть эмпирическое подтверждение, что условия в любой области пространства могут меняться достаточно произвольно. Так что у нас есть подтверждение что любые такие ограничения в действительности в мире не существуют. Следовательно, у нас есть подтверждение, что не существует ЗВК в нашем мире или в мире, отдаленно похожем на наш. Мы изучим этот аргумент более детально, представив четыре возможных ответа со встречными ответами на этот аргумент.

Ответ № 1. Нет ничего неправдоподобного или нового в таких ограничениях. Например, если Вселенная замкнута в пространстве, то должно быть достаточно материи, чтобы образовать необходимую кривизну, и это налагает условия на распределение материи в пространственноподобной гиперповерхности. Поэтому структура глобального пространственно-временного континуума может без проблем вполне ограничить распределение материи на заключенной в нем пространственноподобной поверхности. Более того, у нас нет никакого реалистичного представления, как должны выглядеть эти ограничения, так что мы едва можем иметь подтверждение из существования.

Встречный ответ № 1. Конечно же существуют ограничивающие соотношения между глобальной структурой пространственно-временного континуума и материей в нем. Уравнения Эйнштейна соотносят кривизну многообразия с материей, заключенной в нем. Однако странным и неправдоподобным в ограничениях, наложенных замкнутыми времениподобными кривыми, является то, что эти ограничения, по сути, не имеют ничего общего с уравнениями Эйнштейна. Исследуя такие ограничения, мы обычно рассматриваем частицы и/или поля как тестовые частицы и/или поля данного континуума, т. е. мы принимаем, что они никоим образом не затрагивают размерность континуума. В типичном континууме без замкнутых времениподобных кривых это означает, что мы имеем, по сути, полную свободу распределения материи по пространственноподобной гиперповерхности (для дальнейшего обсуждения этого вопроса см. ответ № 2). Ограничения, наложенные возможностью путешествий во времени, имеют другое происхождение и являются неправдоподобными. В простом случае имеет место причинное взаимодействие между материей и континуумом, приводящее к определенным соотношениям между глобальной структурой пространственно-временного континуума и распределением материи в нем. В случае путешествий во времени нет соотношений причинности: должна быть только предопределенная гармония между глобальной структурой пространственно-временного континуума и распределением материи на пространственноподобных поверхностях. Это неправдоподобно.

Ответ № 2. Ограничения, распространяющиеся на распределения материи, не являются ничем новым. Например, уравнения Максвелла ограничивают электрическое поле E на начальной поверхности таким образом, что оно соотносится с распределением плотности заряда ρ (происходящем одновременно) как уравнение ρ = div(E). Если мы предположим, что поле E сгенерировано только распределением заряда, то это условие подразумевает, что поле E в любой точке пространства будет просто сгенерировано распределением заряда в соответствии с законом Кулона — электростатическим законом обратных квадратов. Это не является неправдоподобной «божественной гармонией». Такие ограничения могут рассматриваться как смысл физического закона. Более того, если бы мы сделали вывод из явного произвольного изменения условий, налагаемых на области пространства, что не могло бы быть таких ограничений, мы бы ошибочно сделали вывод, что выражение ρ = div(E) не может быть законом природы.

Встречный ответ № 2. Ограничения, налагаемые существованием замкнутых времениподобных кривых, резко отличаются от ограничения формулы ρ = div(E). Ограничения формулы ρ = div(E), налагаемые на состояния на пространственноподобной гиперповерхности: 1) локальные ограничения (т. е. позволяющие проверить, действует ли ограничение в области, которую нужно рассмотреть или оно распространяется на все точки области), 2) довольно независимые от глобальной структуры пространственно-временного континуума, 3) довольно независимые от того, как пространственноподобная поверхность, о которой мы говорим, интегрирована в пространственно-временной континуум и 4) очень простые, определяемые в общем виде. С другой стороны, ограничения согласованности, возникающие из-за наличия замкнутых времениподобных кривых 1) не являются локальными, 2) зависят от глобальной структуры континуума, 3) зависят от расположения данной пространственноподобной кривой в данном континууме и 4) формулируются с тем требованием, что состояние на данной пространственноподобной кривой, встроенной определенным образом в данный континуум, не приводят к несогласованности. С точки зрения законов (например, точка зрения Дэвида Льюиса) эта правдоподобность подразумевает, что такие ограничения, даже если они сохраняются, не могут, вероятно, быть законами. Но даже если мы не принимаем такую точку зрения на законы, то можно утверждать, что странные особенности таких ограничений означают неправдоподобность таких ограничений в нашем или любом другом мире, хотя бы отдаленно похожем на наш.

Ответ № 3. Было бы странно, если бы существовали ограничения в области, где путешествий во времени нет. То, что в области путешествий во времени существуют ограничения, не является странным. Их следует объяснить в терминах странных самовзаимодействующих особенностей характера области путешествий во времени. В этой области есть времениподобные траектории, исходящие из точек и возвращающиеся в них. Состояние в такой точке в такой области будет, в некотором смысле, взаимодействовать с самим собой. Хорошо известным является тот факт, что системы, взаимодействующие с самими собой, придут к состоянию равновесия, если такое состояние в принципе существует, или, в противном случае, придут к некоторой сингулярности. Обычно такое самовзаимодействие системы самой собой не является строго мгновенным, оно включает в себя механизм действия обратной связи, на осуществление которого требуется время. Но в областях путешествий во времени происходит нечто подобное мгновенному самовзаимодействию. Это утверждение объясняет, почему во областях путешествий во времени возникают ограничения: состояния «от начала» должны быть «равновесными состояниями». На самом деле это утверждение также иллюстрирует, почему в области путешествий во времени появляется индетерминизм: в начале самовзаимодействий состояния как бы расщепляются на различные одинаково возможные состояния равновесия.

Встречный ответ № 3. Это объяснение — грубая аналогия. Все это показывает, что путешествие во времени приводит к таким странным последствиям, что маловероятно, что это произойдет в мире, отдаленно похожем на наш.

Ответ № 4. Все предыдущее обсуждение полностью игнорирует этот момент. До сих пор мы принимали структуру континуума как данную и ставили вопрос, налагает ли структура континуума ограничения на какие-либо состояния, расположенные на пространственноподобных поверхностях или их частях. Однако континуум и материя взаимодействуют. Предположим, что некто находится в континууме с такими замкнутыми времениподобными линиями, что определенные контрафактивные распределения материи в окрестности точки p исключены, если структура пространственно-временного континуума неподвижна. Тогда можно спросить: «Почему настоящее состояние в окрестности p удовлетворяет этим ограничениям? Какая необыкновенная удача или «божественный план» делает это локальное состояние совместимым с глобальной структурой пространственно-временного континуума? А что бы произошло, если условия вблизи p несколько бы отличались? И можно было бы принять, что отсутствие нормальных ответов на эти вопросы показывает, что очень неправдоподобно, что наш или отдаленно похожий на наш мир допускает путешествия во времени. Однако подходящий ответ на эти вопросы состоит в следующем. Во всяком значительном смысле ограничений не существует. Если они вступают в действие, то они это делают как суть случайного факта, а не закона. Не существует более возможного объяснения для них, чем объяснение случайного факта. Если бы условия в окрестности p были другими, то глобальная структура континуума была бы другой. Так что же? Единственный вопрос, относящийся к проблеме ограничений, состоит в том, всегда ли может произвольное состояние на произвольной поверхности S быть вставлено в континуум так, чтобы состояние на S согласованно доходило до решения для всего континуума.

Но мы знаем ответ на этот вопрос. Хорошо известная теорема из общей теории относительности гласит следующее: любые начальные данные, нанесенные на трехмерное многообразие S с определенной положительной метрической системой, могут быть единственным образом инкорпорированы в максимальный континуум, в котором S является поверхностью Коши (чтобы узнать об этом больше, см. Герох и Горовиц, 1979, с. 284), т. е. существует единственный наибольший континуум, в котором S — поверхность Коши и в котором возможна эволюция начальных данных на S. Теперь, поскольку S является поверхностью Коши, этот континуум не имеет замкнутых времениподобных кривых. Но континуум может иметь расширения (в которых S не является поверхностью Коши), которые включают замкнутые времениподобные кривые; в реальности может быть так, что любое максимально расширение континуума будет включать замкнутые времениподобные кривые. Оказывается, что это представляет собой случай расширений состояний на определенных поверхностях континуумов Тауба-НУТ (см. Ирмэн, Сминк и Вютрих, 2003 в разделе «Другие интернет-ресурсы»). Но конечно, эти расширения будут согласованными. Говоря корректно, для состояний на пространственноподобных поверхностях, ограничений не существует. Тем не менее континуум, в котором поверхности инкорпорированы, может включать, а может и не включать замкнутые времениподобные кривые.

Встречный ответ № 4. Это, по сути, «железобетонный» ответ, на который мы указали в начале раздела 2. Однако не имеет значение, назовем ли мы или нет ограничения, наложенные данным континуумом на распределения материи на определенных пространственноподобных поверхностях «истинными ограничениями», могут они или нет быть рассмотрены наподобие законов и нуждаются ли они в объяснениях: существование таких ограничений все еще можно использовать, чтобы поспорить о том, что миры путешествий во времени являются чем-то настолько странным, что в нашем или в отдаленно похожем на него мире такие путешествия неправдоподобны.

Предположим, что мы находимся в мире путешествий во времени. Предположим, что при данной глобальной пространственно-временной структуре этого мира существуют ограничения, налагаемые, например, на движение шара по пространственно-подобной поверхности, когда его рассматривают как тестовую частицу, т. е. когда предполагается, что шар не затрагивает метрические свойства континуума, в котором он находится. Существует множество другой материи, которая по уравнению Эйнштейна в точности соответствует кривизне, существующей везде в мирах путешествий во времени. Естественно, реальный шар имеет воздействие на метрическую систему континуума, в котором он находится. Но мы рассмотрим шар настолько малый, что его воздействие на метрическую систему пренебрежимо мало. Предположительно, это будет тот же случай, когда определенные состояния этого шара на той пространственноподобной поверхности не будут совместимыми с глобальной структурой путешествий во времени в данной Вселенной.

Это означает, что актуальное распределение материи на такой пространственноподобной поверхности будет продолжено в континуум с замкнутыми времениподобными линиями, а также то, что определенные контрафактивные распределения на пространственноподобной поверхности не могут быть продолжены в тот же самый континуум. Но заметьте, что изменения, привнесенные в распределение материи (при переходе от актуального к контрафактивному распределению) не оказывают влияния на метрические свойства континуума. Таким образом, причина, по которой глобальные свойства (в контексте путешествий во времени) контрафактивного континуума должны существенно отличаться от актуального континуума, заключается не в том, что существуют проблемы с метрическими сингулярностями или изменениями в метрической системе, которые вызывают значительные глобальные изменения при переходе к контрафактивному распределению материи. Причина того, что контрафактивный континуум должен отличаться, состоит в том, что в контрафактивном мире начальное состояние шара в движении, начинающееся на пространственноподобной поверхности, не может согласованно «встретиться» со своей более ранней копией (не может быть согласованно продлено), если бы мы позволили глобальной структуре контрафактивного континуума быть такой же, как и структура настоящего континуума. Не представляется странным или неправдоподобным то, что существует контрафактивная зависимость структуры многообразия, даже его топологии от распределений материи на пространственноподобных поверхностях. Например, некоторые распределения материи могут приводить к сингулярностям, а другие — нет. Мы можем случайно стать, в какой-то мере, обладателями силы воздействия на топологию пространственно-временного континуума, в котором мы живем. Но наличие этой силы очевидно выводится через уравнения Эйнштейна. Но было бы странно думать, что должна была быть контрафактивная зависимость глобальной структуры континуума от расположения определенных мелких частей материи от некоей пространственноподобной поверхности, на которой изменения в расположении по предположению никаким значительным образом не затрагивают метрическую систему в континууме. Это неправдоподобно, что мы живем в таком мире или то, что мир, даже отдаленно похожий на наш, является именно таким.

Проиллюстрируем этот аргумент другим способом, принимая, что путешествия во времени через кротовые норы налагает ограничения, на состояния людей, перед таким путешествием во времени, где люди имеют такую низкую массу/энергию, что они оказывают пренебрежимо малое влияние на локальные метрические свойства (по уравнению Эйнштейна). Думаете ли вы, что более правдоподобным является то, что мы живем в мире, в котором происходят путешествия во времени через кротовые норы, но они происходят только в том случае, когда состояния людей таковы, что эти локальные состояния сочетаются с путешествиями во времени таким образом, что никто не сумеет убить себя более раннего, или вы думаете что более правдоподобно то, что мы находимся в мире без кротовых нор?

Квантовая механика нам поможет?

Существовала особенно ясная формулировка путешествий во времени в контексте квантовой механики, которую предложил исследователь Дэвид Дойч (см. Дойч, 1991; Дойч и Локвуд, 1994) в которой утверждалось, что построения квантовой механики показывают, что путешествия во времени никогда не налагают никаких ограничений на состояние системы до такого путешествия. Суть этой формулировки в следующем.

Квантовая система начинает в состоянии S1, взаимодействует со своей более старой копией, а затем, после того, как взаимодействие перешло в состояние S2, путешествует во времени, переходя в состояние S3, затем взаимодействует со своей более ранней копией и заканчивает в состоянии S4 (см. рисунок 13).

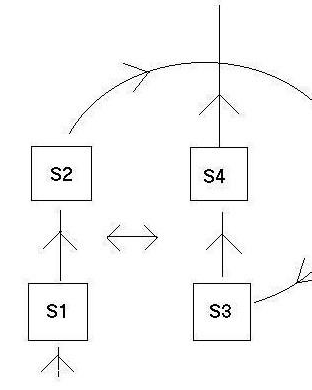
Рисунок 13

Дойч предположил, что набор возможных состояний этой системы находится в смешанных состояниях, т. е. представлены в виде матриц плотности в Гильбертовом пространстве системы. Далее Дойч показывает что для любого начального состояния S1, любого единичного взаимодействия между более старой и более ранней системой и любого единичного развития в процессе перемещения во времени найдется согласованное решение, т. е. найдется хотя бы одна пара таких состояний S2 и S3, при которых она перейдет в состояние S2, когда S1 реагирует с S3, а S2 перейдет в таком случае в S3. Состояния S2, S3 и S4 будут не чистыми, а нетривиальными смешанными состояниями, даже если S1 — чистое. Чтобы понять, как это приводит к проблемам интерпретации, приведем пример. Рассмотрим систему с двумерным Гильбертовым пространством с базисом в состояниях и . Предположим, что когда состояние ранней копии системы встречается с состоянием более старой копии системы, системы взаимодействуют, и ранняя система переходит в состояние , а старая система остается в состоянии . В явных обозначениях:

13 переходит в 24.

Похожим образом, предположим, что:

13 переходит в 24,

13 переходит в 24,

13 переходит в 24.

Далее предположим, что в процессе путешествий во времени переходов между состояниями не наблюдается, т. е. 2 переходит в 3, а 2 переходит в 3.

Теперь, если единственными возможными состояниями системы были бы и (т. е. если бы не было суперпозиций или смешения этих состояний), возникло бы ограничение на начальные состояния: состояние 1 невозможно. Если 1 взаимодействует с 3, то оно перейдет в 2, которое в течение путешествия во времени перейдет в 3, которое является несогласованным с принятым состоянием 3. Похожим образом, если 1 взаимодействует с 3, то оно перейдет в 2, которое тогда перейдет в 3, которое также несогласованно. Таким образом, система не может начинать действия в состоянии 1.

Но, как говорит Дойч, в квантовой механике такая система также может находиться в любом сочетании состояний и . Предположим, что более старая копия системы до взаимодействия находится в состоянии S3, которое представляет собой смесь равных частей — 50 % 3 и 50 % 3. Тогда более ранняя копия системы во время взаимодействия перейдет в сочетание 50 % 2 и 50 % 2, которая затем превратится в сочетание 50 % 3 и 50 % 3, что является согласованным! В более общем смысле Дойч использует теорему о неподвижных точках, чтобы показать, что единичное развитие системы во время взаимодействия не имеет значения, и неважно, каким является единичное развитие в процессе перемещений во времени — для любого состояния S1 всегда найдется состояние S3, которое не является чистыми состоянием и которое заставляет S1 переходить в состояние S2, которое, в свою очередь, переходит в состояние S3. Таким образом, квантовая механика приходит на помощь: она показывает полностью в общем виде, что начальное состояние не требует никаких ограничений!

Можно поинтересоваться, почему Дойч говорит о смешанных состояниях: являются ли недостаточными суперпозиции состояний и ? К сожалению, такая идея не работает. Предположим снова, что начальным состоянием является 1. Можно предположить, что если состояние S3 выражается через 1/√2 3 + 1/√2 3, то мы получим согласованное развитие. Можно представить, что когда начальное состояние 1 встречается с суперпозицией 1/√2 3 + 1/√2 3, оно переходит в суперпозицию 1/√2 2 + 1/√2 2, и что эта суперпозиция, в свою очередь, превращается в 1/√2 3 + 1/√2 3, как мы этого и хотим. Однако это не корректно. Для начального состояния 1 при встрече с 1/√2 3 + 1/√2 3, осуществляется переход в переплетенное состояние 1/√2 24 + 1/√2 24. Поэтому можно говорить о состоянии ранней системы после этого взаимодействия: оно представляет собой сочетание 50 % 2 и 50 % 2, а не суперпозицию 1/√2 2 + 1/√2 2. Так что Дойчу действительно необходимо использовать смешанные состояния.

Разъяснение того, почему Дойч имеет необходимость в использовании смешанных состояний не указывает на серьезную причину для беспокойства, касающуюся упрощений, которые являются частью рассуждений Дойча. После взаимодействия старая и ранняя копии системы попадает (обычно) в переплетенное состояние. Хотя для выполнения измерений на одной из двух систем можно принять, что система находится в смешанном состоянии, невозможно представить полное состояние двух систем, определяя смешанное состояние каждой отдельной части, поскольку существуют корреляции между различными наблюдаемыми частями двух систем, не показанные этими двумя смешанными состояниями, но представленные в соединенном переплетенном состоянии. Но если действительно существует переплетенное состояние, образованное старой и ранней системой после взаимодействия, то как можно далее показать эволюцию этого состояния? Останется ли состояние ранней системы переплетенным с состоянием ранней системы при том, что ранняя копия системы перемещается во времени, а старая система переходит в будущее? На какой пространственноподобной поверхности должны мы представить это полностью переплетенное состояние? На данном этапе становится ясным, что не существует очевидного и простого способа применить элементарную нерелятивистскую квантовую механику к континуумам с замкнутыми времениподобным кривым. Существуют также более сложные подходы, чем те, которые Дойч применил к путешествиям во времени, используя методический аппарат теории квантового поля и многообразия, поддающиеся дифференцированию (см. Фридман и др., 1991; Ирмэн, Сминк и Вютрих, 2003 в разделе «Другие интернет-ресурсы», а также ссылки в этих работах). Но такие подходы нет дают результатов, приближающихся к решению проблемы таким же ясным и интересным образом, как результаты Дойча.

Как Дойч избегает этих усложнений? Дойч предполагает, что более старая копия системы S3 находится в смешанном состоянии перед тем, как она взаимодействует с более ранней копией системы. Он позволяет ей взаимодействовать с более ранней копией системы, находящейся в произвольно чистом состоянии S1. После этого взаимодействия наступает «переплетенное» состояние S′ двух систем. Дойч вычисляет смешанное состояние S2 более ранней копии системы, которое налагает это переплетенное состояние S′. Его требование согласованности тогда состоит лишь в том, что это смешанное состояние S2 переходит в смешанное состояние S3. Сейчас не совсем ясно, что это представляет собой законный путь для упрощения проблемы путешествий во времени в контексте квантовой механики. Но даже если мы поставим Дойчу в заслугу это упрощение, то проблема остается: как нам понимать эти смешанные системы?

Если мы будем интерпретировать их путем игнорирования чего-либо, то мы придем к затруднениям. Предположив, что в каждом отдельном случае каждая старая система находится или в состоянии 3, или в состоянии 3 перед взаимодействием, мы вернемся к нашему парадоксу. Вместо этого Дойч рекомендует следующее: много миров, смешанные состояния. Предположим, что мы начинаем в состоянии 1 во всех мирах. В некоторых из многих миров более старая копия системы будет в состоянии 3, назовем их «A-миры», и в некоторых мирах, назовем их «B-миры», она будет в состоянии 3. Таким образом, в A-мирах после взаимодействия мы придем к состоянию 2, а в B-мирах мы придем к 2. В время путешествия во времени состояние 2 останется тем же самым, т. е. перейдет в состояние 3, но система, о которой мы говорим, перейдет из A-миров в B-миры. Похожим образом состояния 2 перейдут из B-миров в A-миры, сохраняя согласованность.

Теперь, что бы не думали о пользе от интерпретаций множества миров и рассмотрения смешанных состояний, в конце концов мы не получим истинного путешествия во времени в рамках построений Дойча. Системы, о которых мы говорим, переходят от одного времени в одном мире к другому времени в другом мире, но при этом никакая система не перемещается в более раннее время в одном и том же мире (это верно по крайней мере в обычном смысле слова «мир», т. е. смысле, подразумеваемом, когда говорят, например: «Был и будет только один Элвис Пресли в мире»). Следовательно, даже если бы это был разумный взгляд, это не настолько интересно, как оно могло казаться в начале.

Выводы

После всего вышесказанного парадокс, связанный с убийством более ранней копии самого себя, в общих релятивистских мирах, где осуществляются путешествия во времени, заключается в том, что в некоторых случаях состояния на бескрайних пространственноподобных поверхностях «сверхограничены». Так что у нас нечто меньшее, чем обычная свобода задавать условия на такой поверхности, определять данную структуру путешествий во времени. А в некоторых случаях такие состояния «недоограничены», т. е. такие состояния на пространственноподобных поверхностях не определяют то, что происходит где-либо еще и не задают структуру перемещений во времени. Могут быть также сочетания этих двух типов состояний. То, в какой степени состояния сверхограничены и/или недоограничены, в реалистичных моделях до конца не выяснено. Хотя, если бы такой результат появился, то это было бы удивительно. Существующая литература первоначально сконцентрировалась на проблеме сверхограничения, поскольку часто ее рассматривают или как метафизическое препятствие на пути к перемещениям во времени, или как эпистемологическое препятствие к правдоподобию таких перемещений в нашем мире. Пока же верно то, что наш мир являлся бы довольно отличным от того, как мы обычно его представляем, если состояния были бы сверхограниченными, а недоограничение представляется по крайней мере настолько же странным, как и сверхограничение. Тем не менее полностью исключить возможность путешествий во времени нельзя.

Если бы перемещение во времени влекло за собой противоречия, то мы бы неизбежно к ним пришли. И в самом деле, большинство популярных художественных произведений, в которых происходят путешествия во времени, логически непоследовательны: невозможно изменить прошлое и изменить то, что было, поскольку прошлое (так же, как и настоящее и будущее) случается только однажды. Но если бы единственным требованием была бы логическая последовательность, то все было бы слишком просто. Умный автор может придумать последовательный сценарий, в котором все события происходят согласованным образом только по одному разу. Это слишком просто: логическая последовательность является очень слабым условием, и многие вещи, которые мы считаем метафизически невозможными, обладают логической последовательностью. Например, для нее нет логического противоречия в том, чтобы считать, что у воды нет молекулярной структуры, но если химия и Крипке правы, то это — метафизическая невозможность. Мы были заинтересованы не в логической, а в физической возможности. Но даже в таком случае наши условия относительно слабы: мы задали вопрос лишь о том, совместимы ли путешествия во времени с универсальной действительностью физических законов и с утверждением о том, что физическое состояние на поверхности перед перемещением во времени не имеет ограничений. Вполне возможно, что физические законы подчиняются этому условию, но путешествия во времени пока еще невозможны метафизически из-за природы времени как такового. Рассмотрим аналогию. Аристотель считал, что вода гомоморфна и бесконечно делима: любая часть воды может быть в принципе разделена на меньшие части воды. Взгляд Аристотеля не содержит логического противоречия. Он являлся определенно согласованным с представлением Аристотеля о воде, о том, что она гомоморфна, и это было для него концептуальной возможностью. Но если химия права, то Аристотель не был прав и в том, что собой представляет вода, и в том, что для нее возможно. Она не может быть бесконечно делима, даже если этого не выявит никакой логический или концептуальный анализ.

Похожим образом, если будут соблюдены все наши условия согласованности, то из этого не следует, что путешествия во времени возможны физически. Из этого следует лишь то, что некоторые особые физические построения не могут исключить этого. Единственным серьезным доказательством путешествий во времени будет их наглядная демонстрация. Если мы согласимся, что в нашей Вселенной не существует реальных путешествий во времени, то предположение, что они могли были быть, заставляет нас постулировать значительное различие с реальностью, постулировать, что все вещи в этом мире не являются первичными. Для нас не вполне ясно, насколько это было бы возможно, если бы кто-то стал поддерживать или отрицать возможность путешествий во времени в этих обстоятельствах, если бы кто-то явно не обозначил, что такая возможность не исключается набором ограничений. Как показывает пример с теорией воды Аристотеля, концептуальная и логическая возможность не влекут за собой возможность в полноценном смысле. Каким был бы полноценный смысл в случае путешествий во времени и можно ли иметь основание добиться его, остается для нас неизвестным.

Библиография

1. Deutsch, D. 1991. “Quantum mechanics near closed timelike curves,” Physical Review D, 44: 3197-3217.
2. Deutsch, D. and Lockwood, M. 1994. “The quantum physics of time travel,” Scientific American, 270 (3): 68-74.
3. Earman, J. 1972. “Implications of causal propagation outsider the null cone,” in Foundations of Space-Time Theory, Minnesota Studies in the Philosophy of Science, Vol VII, Earman, J., Glymour, C., and Stachel, J. (eds), pp. 94-108. Minneapolis: University of Minnesota Press.
4. Earman, J. 1995. Bangs, Crunches, Whimpers and Shrieks: Singularities and Acausalities in Relativistic Spacetimes, New York: Oxford University Press.
5. Earman, J., Smeenk, C., and Wüthrich, C. 2009.“Do the laws of physics forbid the operation of a time machine?,” Synthese, 169 (1): 91-124.
6. Echeverria, F., Klinkhammer, G., and Thorne, K. 1991. “Billiard ball in wormhole spacetimes with closed timelike curves: classical theory,” Physical Review D, 44 (4): 1077-1099.
7. Friedman, J. et al. 1990. “Cauchy problem in spacetimes with closed timelike lines,” Physical Review D, 42: 1915-1930.
8. Friedman, J. and Morris, M. 1991. “The Cauchy problem for the scalar wave equation is well defined on a class of spacetimes with closed timelike curves,” Physical Review letters, 66: 401-404.
9. Geroch, R. and Horowitz, G. 1979. “Global structures of spacetimes,” in General Relativity, an Einstein Centenary Survey, S. Hawking and W. Israel (eds.), Cambridge: Cambridge University Press.
10. Gödel, K. 1949. “A remark about the relationship between relativity theory and idealistic philosophy,” in Albert Einstein: Philosopher-Scientist, P. Schilpp (ed.), La Salle: Open Court, pp. 557-562.
11. Hocking, J., and Young, G. 1961. Topology, New York: Dover Publications.
12. Horwich, P. 1987. “Time travel,” in Asymmetries in time, Cambridge, MA: MIT Press.
13. Kutach, D. 2003. “Time travel and consistency constraint”, Philosophy of Science, 70: 1098-1113.
14. Malament, D. 1985a. “’Time travel’ in the Gödel universe,” PSA 1984, 2: 91-100, P. Asquith and P. Kitcher (eds.), East Lansing, MI: Philosophy of Science Association.
15. Malament, D. 1985b. “Minimal acceleration requirements for ‘time travel’ in Gödel spacetime,” Journal of Mathematical Physics, 26: 774-777.
16. Maudlin, T. 1990. “Time Travel and topology,” PSA 1990, 1: 303-315, East Lansing, MI: Philosophy of Science Association.
17. Novikov, I. 1992. “Time machine and self-consistent evolution in problems with self-interaction,” Physical Review D, 45: 1989-1994.
18. Thorne, K. 1994. Black Holes and Time Warps, Einstein's Outrageous Legacy, London and New York: W.W. Norton.
19. Wheeler, J. and Feynman, R. 1949. “Classical electrodynamics in terms of direct interparticle action,” Reviews of Modern Physics, 21: 425-434.
20. Yurtsever, U. 1990. “Test fields on compact space-times,” Journal of Mathematical Physics, 31: 3064-3078.

Другие Интернет ресурсы

1. Earman, J., Smeenk, C. and Wüthrich, C., 2003, “Take a ride on a time machine”, manuscript available at the PhilSci Archive, University of Pittsburgh.
2. Time Travel in Flatland (Cal Tech Particle Theory Group)

Связанные статьи

determinism: causal | Gödel, Kurt: contributions to relativity theory | time machines | time travel