диспуты

Поделиться статьей в социальных сетях:

в избранное

Самореференция

Ссылка на оригинал: Stanford Encyclopedia of Philosophy

Впервые опубликовано 15 июля 2008 года; содержательно переработано 31 августа 2017 года.

В языковом контексте понятие «самореференция» используется для обозначения утверждения, которое отсылает к себе самому или к своему референту. Наиболее известным примером такого суждения является предложение лжеца: «Это суждение ложно». Термин «самореференция» часто употребляется и в более широком контексте. Так, изображение считается самореферентным, если содержит копию себя (см. анимацию выше), а также литературное произведение — если в нем есть отсылка к себе самому. В рамках философии самореференция в первую очередь изучается в языковом контексте. Самореференция в языке — это не только предмет философии, но и область особого интереса в математике и информатике, в частности, в связи с основаниями этих наук.

Философия интерес к самореференции в значительной степени сосредоточен вокруг парадоксов. Парадокс — рассуждение, кажущееся здравым, исходящее из истинных, по видимости, допущений, однако приводящее к противоречию. Рассмотренное выше предложение лжеца ведет к противоречию, когда мы пытаемся установить его истинность. Если допустить, что это предложение истинно, должно иметь место то, о чем говорится, то есть предложение не может быть истинным. Если, с другой стороны, предположить, что это не так, выходит, что утверждаемое на самом деле не имеет места, а следовательно, предложение лжеца должно быть истинным. В любом случае выходит противоречие. Поскольку же оно было получено с помощью здравого, казалось бы, рассуждения, опирающегося на истинные, по всей видимости, допущения, предложение с этим противоречием называют парадокс. Оно известно как парадокс лжеца.

Семантические парадоксы, такие как парадокс лжеца, в первую очередь имеют отношение к теориям истины. Теоретико-множественные парадоксы связаны с основаниями математики, а эпистемические парадоксы — с эпистемологией. Несмотря на то, что парадоксы различаются по предмету, к которому относятся, структура у них в основном совпадает, и их часто можно разрешить с использованием одних и тех же математических средств.

В настоящей статье сначала мы представим ряд наиболее известных парадоксов самореференции и обсудим их общую базовую структуру. Далее мы обсудим проистекающие из них глубокие последствия для ряда различных областей: теории истины, теории множеств, эпистемологии, оснований математики, вычислимости. Наконец, мы представим наиболее известные подходы к решению парадоксов.

Парадоксы самореференции

Семантические парадоксы

Парадоксы самореференции известны с древних времен. Открытие парадокса лжеца чаще всего приписывают мегарику Евбулиду, который жил в IV в. до н.э. Парадокс лжеца относится к категории семантических, поскольку опирается на семантическое понятие истины. К другим хорошо известным семантическим парадоксам относятся парадоксы Греллинга, Берри и Ришара.

Парадокс Греллинга включает в себя предикат, определяемый следующим образом. Предикат называется гетерологичным, если не описывает сам себя, т.е. если сам не обладает выражаемым им свойством. К примеру, предикат «немецкий» гетерологичен, поскольку не является немецким словом, а предикат «deutsch» не гетерологичен. Вопрос, приводящий к парадоксу, звучит так:

Гетерологичен ли предикат «гетерологичный»?

Нетрудно увидеть, что противоречие возникает вне зависимости от того, отвечаем ли мы «да» или «нет» на этот вопрос (аргументация здесь более или менее схожа с парадоксом лжеца). Парадокс Греллинга самореферентен, так как определение предиката «гетерологичный» относится ко всем предикатам, включая предикат «гетерологичный». Подобные определения, которые опираются на множество элементов, по крайней мере один из которых входит в круг определяемых, называются непредикативными.

Парадокс Берри точно так же основывается на непредикативном определении или, если точнее, описании. Некоторые фразы естественного языка описывают натуральные числа, например, «сумма пяти и семи» — это описание числа 12. Парадокс Берри возникает при попытке определить денотат следующего описания:

наименьшее натуральное число, которое нельзя описать менее чем одиннадцатью словами.

Противоречие в том, что это описание из десяти слов обозначает число, которое по определению нельзя обозначить описанием, содержащим менее одиннадцати слов. Это описание непредикативно, разумеется, поскольку имплицитно относится ко всем описаниям, включая само себя.

Парадокс Ришара касается тех фраз естественного языка, которые определяют вещественные числа, а не натуральные. Например, «соотношение между окружностью и диаметром круга» — определение числа π. Допустим, приведено перечисление всех таких фраз (дано в лексикографическом порядке, скажем). Теперь рассмотрим фразу:

вещественное число, чей n-й десятичный знак равен 1, когда n-й десятичный знак числа, обозначаемого n-й фразой, равен 0; в противном случае 0.

Фраза определяет вещественное число, поэтому должна быть среди перечисленных определений, скажем, числа k в этом перечислении. Но в то же время, по определению, оно отличается от числа, обозначаемого k-й фразой в k-м десятичном знаке. Возникает противоречие. Определение, очевидно, непредикативно. Построение, применяемое здесь, является разновидностью диагонализации.

Он также лег в основу парадокса Кантора, одного из теоретико-множественных парадоксов, которые будут рассмотрены ниже.

Теоретико-множественные парадоксы

Наиболее известные парадоксы теории множеств — это парадоксы Рассела и Кантора. Парадокс Рассела возникает при рассмотрении множества Рассела R всех множеств, которые не входят сами в себя, заданного как R={x∣x∉x}. Противоречие выводится, когда мы спрашиваем, не принадлежит ли само R себе, то есть справедливо ли R∈R. Если R∈R, то R принадлежит себе, а следовательно, R∉R, по определению R. Если, с другой стороны, R∉R, то R не принадлежит себе, а следовательно, R∈R, опять же по определению R.

Парадокс Кантора проистекает из применения теоремы Кантора. Теорема Кантора гласит: при любом конечном или бесконечном множестве S его степенное множество строго больше по своей мощности (размеру), чем S. Теорема доказывается путем диагонализации, идея здесь та же самая, что в случае парадокса Ришара. В парадоксе Кантора рассматривается множество всех множеств. Пусть оно называется универсальным множеством U. Степенное множество U обозначается как ℘(U). Так как U содержит все множества, в частности, оно будет содержать все элементы ℘(U). Таким образом, ℘(U) должно быть подмножеством U, а следовательно, мощность ℘(U) меньше или равна мощности U. Однако этот результат противоречит теореме Кантора.

Относительно недавно перечень теоретико-множественных парадоксов пополнил парадокс гиперигры, изобретенный Цвикером (Zwicker 1987). Назовем игру с двумя игроками конечной (или вполне фундированной — well-founded), если она обязательно закончится за конечное число ходов. Турнирные шахматы — пример конечной игры. Теперь мы определяем гиперигру как игру, в которой игрок 1 на первом ходу выбирает для игры конечную игру, а игрок 2 впоследствии делает первый ход в выбранной игре. Оставшиеся ходы тогда являются ходами выбранной игры. Гиперигра должна быть конечной, так как любая игра будет длиться ровно на один ход больше, чем какая-либо выбранная конечная игра. Однако если гиперигра конечна, то относится к играм, которые доступны для выбора на первом ходу гиперигры, а стало быть, игрок 1 может выбрать гиперигру на первом ходу, а игрок 2 — на следующем ходу, и они могут выбирать гиперигры до бесконечности. А значит, гиперигра не вполне фундирована, что противоречит нашему предыдущему выводу.

Эпистемические парадоксы

Самым известным среди эпистемических является парадокс познающего (paradox of the knower). Имеется множество эквивалентных формулировок парадокса, одна из них основана на предложении «Это предложение никем не познано». Назовем его предложением познающего, сокращенно ПП.

Вывод противоречия из ПП несколько сложнее, чем в парадоксе лжеца. Сначала истинность ПП показывается в следующем рассуждении:

Чтобы прийти к противоречию, допустим, что ПП ложно. Тогда то, что выражает ПП, не может иметь место, иными словами, ПП должно быть кем-то познано. Поскольку все познанное истинно (по определению познаний), ПП истинно, что противоречит нашему допущению. Отсюда следует, что ПП истинно.

Ход рассуждений, только что использованный для доказательства истинности ПП, должен быть доступен любому агенту (лицу) с достаточными возможностями суждения. То есть агент должен быть способен доказать истинность ПП — и таким образом узнать, что ПП имеет место. Однако если ПП познано, то выражаемое им не имеет места, а следовательно, не может быть истинным. В итоге мы имеем противоречие, а стало быть, и парадокс. Роль самореференции в нем очевидна, поскольку парадокс основан на предложении, относящемся непосредственно к самому себе, — ПП.

Парадокс познающего — лишь один среди многих эпистемических парадоксов самореференции. Для получения дополнительных сведений см. статью об эпистемических парадоксах. В последние годы их перечень пополнил парадокс Бранденбургера-Кейслера (Brandenburger & Keisler 2006), который возник в контексте убеждений и предположений в игре для двух игроков; см. подробный его разбор в статье об эпистемических основаниях теории игр. История парадоксов самореференции в целом и подробное обсуждение см. в статье о парадоксах и современной логике.

Общие структуры парадоксов

Вышеперечисленные парадоксы весьма схожи по структуре. В случае парадоксов Греллинга и Рассела это демонстрируется следующим образом. Давайте зададим объем предиката как множество объектов, для которых он истинен. Для предиката P объем будет обозначаться как ext(P). Парадокс Греллинга включает в себя предикат «гетерологический», который истинен для всех тех предикатов, которые неистинны сами по себе. Объемом предиката «гетерологический» выступит множество {P∣P∉ ext(P)}. Сравним с множеством Рассела R, заданным как {x∣x∉x}. Единственное существенное отличие между ними состоит в том, что первое определяется через предикаты, тогда как второе — через множества. Доказательства противоречий, основанные на двух множествах, также имеют одинаковую структуру, как показано ниже (где «het» — краткое обозначение предиката «гетерологический»):

Возникают два парадокса почти с одной и той же структурой, но принадлежат они ко двум разным классам: первый — семантический, а второй — теоретико-множественный. Мы видим здесь, что даже если парадоксы кажутся разными, поскольку затрагивают разные предметы, по своей базовой структуре они могут почти что совпадать. Значит, во многих случаях имеет смысл рассматривать парадоксы самореференции вместе, а не брать по отдельности, скажем, семантические и теоретико-множественные парадоксы.

В том числе парадоксы Рассела и Кантора похожи больше, чем кажется на первый взгляд. Парадокс Кантора основан на применении теоремы Кантора к универсальному множеству U (ср. выше § 1.2). Ниже приведено доказательство теоремы Кантора для произвольного множества S.

Нужно доказать, что мощность ℘(S) больше, чем у S. Чтобы прийти к противоречию, допустим, что истинно обратное. Тогда должно существовать отображение f из S на ℘(S). Теперь рассмотрим множество C={x∈S∣x∉f(x)}. Так как f отображено на ℘(S), то должно существовать множество c∈S, такое что f(c)=C. Однако теперь мы приходим к противоречию, ведь справедливо следующее:

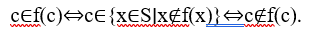
Обратите внимание на сходство между этой чередой эквивалентностей и соответствующими рядами эквивалентностей, полученными выше для парадоксов Рассела и Греллинга. Рассмотрим теперь частный случай теоремы Кантора, где S — универсальное множество. Можно просто выбрать f как функцию тождественности, поскольку ℘(U) с необходимостью должно быть подмножеством универсального множества U. Но C становится в таком случае множеством Рассела!

Прист (Priest 1994) приводит даже еще более убедительные свидетельства в пользу схожести парадоксов самореференции. Он показывает, что все они вписываются в то, что он первоначально называл Качественной схемой Рассела (Qualified Russell’s Schema), а в наши дни называется Схемой замыкания. Идея в основании восходит к самому Расселу (Russell 1905), который также считал, что парадоксы самореференции разделяют базовую структуру друг с другом. Если даны два предиката P и Q и возможно частичная функция δ, то схема замыкания состоит из следующих двух условий:

1. w={x∣P(x)} существует, Q(w) имеет место;

2. если y — такое подмножество w, что имеет место Q(y), то:

a. δ(y)∉y,

b. δ(y)∈w.

Если условия выполняются, возникает следующее противоречие: поскольку w тривиально является подмножеством w и поскольку имеет место Q(w), по условию 1, мы имеем и δ(w)∉w, и δ(w)∈w, по 2a и 2b соответственно. Любой триплет (P,Q,δ), удовлетворяющий схеме замыкания, приводит к парадоксу. Прист показывает, что в данную схему вписываются большинство известных парадоксов самореференции. Ниже будут рассмотрены лишь некоторые из них, начиная с парадокса Рассела. В этом случае мы определим триплет (P,Q,δ) так:

• P(x) — это предикат «x∉x».

• Q(y) — универсальный предикат, истинный для любого объекта.

• δ — функция тождественности.

Тогда w в схеме замыкания будет множеством Рассела, а противоречие, полученное из схемы, — парадоксом Рассела.

Для парадокса Ришара мы определим триплет так:

• P(x) — предикат «x — вещественное число, которое определяется фразой обыденного языка».

• Q(y) — предикат «y — перечислимое множество вещественных чисел, которые определяются фразами обыденного языка».

• δ — функция, которая отображает любое перечислимое множество вещественных чисел y на вещественное z, чей n-й десятичный знак равен 1, когда n-й десятичный знак n-го вещественного числа в y равен 0; в противном случае 0. (Подойдет любое перечисление элементов y.)

Здесь w={x∣P(x)} становится множеством всех вещественных чисел, которые можно определить фразами обыденного языка. Для любого перечислимого подмножества y из w окажется вещественным δ(y), которое по определению будет отличаться от всех вещественных чисел в y (оно отличается от n-го вещественного числа в y на n-м десятичном знаке). Если y равняется w, мы получаем δ(w)∉w. Но в то же время δ(w) задается фразой обыденного языка, поэтому δ(w)∈w, стало быть, возникает противоречие. Это противоречие и есть парадокс Ришара.

Под схему Рассела подпадает и парадокс лжеца, хотя и не так непосредственно:

• P(x) — предикат «x∉x».

• Q(y) — предикат «y определимо».

• δ(y) — предложение «Это предложение не принадлежит множеству y».

Здесь w={x∣P(x)} будет множеством истинных предложений, а δ(w) — примером предложения лжеца: «Это предложение не принадлежит множеству истинных предложений».

Из вышесказанного можно сделать вывод, что все или по крайней мере большая часть парадоксов самореференции разделяют одну и ту же базовую структуру — вне зависимости от того, являются они семантическими, теоретико-множественными или же эпистемическими. По Присту (Priest 1994), тогда они должны иметь и общее решение. Прист называет это принципом единообразного решения: «Одному типу парадоксов — один тип решений». Однако вопрос о том, может ли схема замыкания считаться условием, необходимым и достаточным для парадоксальности самореференции, является спорным (Slater 2002; Abad 2008; Badici 2008; Zhong 2012 и др.), поэтому не все авторы также согласны с принципом единообразного решения.

Парадокс кучи («Сорит») на первый взгляд не предполагает самореференции вовсе. Но Прист (Priest 2010b, 2013) утверждает, что и он тоже соответствует схеме замыкания, а значит, может рассматриваться как парадокс самореференции или по крайней мере парадокс, решение которого по своему типу совпадает с решением парадоксов самореференции. В результате в работах Colyvan 2009, Priest 2010 и Weber 2010b был выдвинут диалетеический подход к парадоксу кучи. Он был подвергнут критике в Beall 2014a, 2014b и затем отстаивался в Weber et al. 2014.

Парадоксы без отрицания

Большинство рассмотренных здесь парадоксов существенным образом включают отрицание: например, предложениях, говорящие сами о себе, что они не истинны или познаваемы. Ключевая роль отрицания станет еще более ясной, когда мы формализуем парадоксы самореференции в § 2 ниже. Парадокс Карри — схожий парадокс самореференции, который, однако, не задействует отрицание напрямую. Семантический его вариант исходит из предложения Карри (далее — C) «Если это предложение истинно, то F», где F может быть любым утверждением, к примеру, явно ложным. Предположим, C истинно. Тогда оно выражает истинный факт, то есть, если C истинно, то F. Но мы уже предположили, что C истинно, поэтому можем вывести F через modus ponens. Теперь мы доказали, что если предположить, что C истинно, то F. Именно это и выражает само предложение Карри. Другими словами, мы доказали, что само предложение Карри истинно! Но тогда мы также имеем, что F истинно, и это парадокс, поскольку F может быть любым утверждением, включая явно ложные.

В классической логике, где импликация C→F эквивалентна C∨F, парадокс Карри по-прежнему имплицитно задействует отрицание, но он все же интересен сам по себе, поскольку он проходит меньшее количество допущений о лежащей в его основании логике, нежели парадокс лжеца. Более подробный разбор см. в статье о парадоксе Карри.

Парадоксы без самореференции

В 1985 году Ябло преуспел в построении семантического парадокса, который не предполагает самореференции в строгом смысле слова. Вместо этого он состоит из бесконечной цепочки предложений, каждое из которых выражает неистинность всех последующих. Точнее, для каждого натурального числа i мы определяем Si как предложение «Для всех j>i выходит, что Sj ложно». Тогда мы можем вывести противоречие следующим образом:

Сначала докажем, что ни одно из суждений Si не может быть истинным. Чтобы прийти к противоречию, допустим, что Si истинно для некоторого i. Тогда истинно «Для всех j>i выходит, что Sj ложно». Таким образом, ни одно из предложений Sj для j>i не истинно. В частности, Si+1 неистинно. Si+1 — предложение «Для всех j>i+1 выходит, что Sj ложно». Поскольку оно ложно, то должно существовать некоторое k>i+1, для которого Sk истинно. Но это противоречит тому, что ни одно из суждений Sj при j>i не является истинным.

Теперь мы доказали, что ни одно из суждений Si не является истинным. Тогда, в частности, для всех j>0 у нас выходит, что S>j ложно. Это именно то, что выражается S0, поэтому S0 должно быть истинным. Опять-таки, противоречие.

Ябло называет ситуацию парадоксом ω-лжеца, но другие обычно называют ее парадоксом Ябло. Обратите внимание, что ни одно из предложений Si не отсылает к себе (даже косвенно), а только к тем предложениям, которые встречаются позже в последовательности. Это семантический парадокс, но, как показал Ябло (Yablo 2006), подобного рода парадоксы без самореференции формулируемы и для некоторых теорий множеств.

Парадокс Ябло демонстрирует возможность логических парадоксов без самореференции — для вывода противоречия требуется лишь наличие особой разновидности неполной фундированности (non-wellfoundedness). По структуре обычные парадоксы самореференции и парадокс Ябло, разумеется, отличаются: обычные включают в себя циклическую структуру референции, тогда как парадокс Ябло включает нециклическую, но не вполне фундированую структуру референции. Если говорить точнее, структура референции в самореферентных парадоксах, таких как парадокс лжеца, представляет собой не что иное, как рефлексивное отношение к синглетону (циклу), тогда как структура референции в парадоксе Ябло изоморфна обычному возрастающему порядку натуральных чисел, который является строгим полным упорядочиванием (не содержит циклов).

В дальнейшем мы, однако, будем придерживаться термина «парадоксы самореференции», вместе с тем большая часть сказанного будет относиться в том числе к парадоксу Ябло и связанным с ним парадоксам неполной фундированности.

С пониманием того, что не только циклические структуры референции приводят к парадоксам, но и особые типы не вполне фундированных структур, становится интересным дальнейшее изучение этих структур референции и их потенциала в описании перечня условий, необходимых и достаточных для парадоксальности. Это направление работы было начато в Gaifman 1988, 1992, 2000 и продолжено в Cook 2004, Walicki 2009 и др.

В значительном количестве новых работ по самореференции предпринимались попытки дать полное описание того, какие именно структуры референции допускают парадоксы, с точки зрения теории графов (см., напр., Rabern and Macauley 2013, Cook 2014 и Dyrkolbotn and Walicki 2014). Полное описание — вопрос все еще открытый (Rabern, Rabern and Macauley 2013), однако, по-видимому, гипотеза, в соответствии с которой все парадоксальные графы референции циклические либо содержат структуру, схожую со структурой парадокса Ябло, весьма широко распространена. Если гипотеза оправдает себя, это будет означать, что структурно все парадоксы референции похожи либо на парадокс лжеца, либо на парадокс Ябло. Точная характеризация того, что подразумевается под «схожестью с парадоксом Ябло», — также открытый вопрос.

Хотя структура референции в парадоксе Ябло и не содержит циклов (каждое предложение относится только к более поздним в последовательности), все еще обсуждается вопрос, является ли парадокс самореферентным (Cook 2014; Halbach and Zhang 2017). Сам Ябло (Yablo 1993) утверждает, что тот не самореферентен, в то время как Прист (Priest 1997) утверждает обратное. Батлер (Butler 2017) заявляет, что даже если Прист прав, возможны и иные парадоксы, схожие с парадоксом Ябло и не самореферентные в смысле Приста. При анализе парадокса Ябло важно отметить, что он включает бесконечную последовательность предложений, где каждое относится к бесконечному множеству других. Следовательно, чтобы формализовать его в рамках пропозициональной логики, необходимо использовать инфинитную пропозициональную логику. Любой финитный вид последовательности Ябло — где каждое предложение относится лишь к конечному числу более поздних — обязательно должен быть консистентным (непарадоксальным) из-за теоремы компактности в пропозициональной логике (каждое конечное подмножество предложений в последовательности вызывает вполне фундированное отношение референции, а стало быть, суждениям можно непротиворечиво присваивать значения истинности снизу вверх). В финитной арифметике первого и второго порядка вместо этого можно попытаться формализовать парадокс Ябло через одноместный предикат S(x), где S(i) для каждого натурального числа i — это формализация i-го предложения Si ряда Ябло (где i — цифра, представляющая i). То, как парадокс Ябло можно правдоподобно представить таким образом и как именно он связан с компактностью лежащей в его основе логики, было исследовано Пиколло (Picollo 2013).

Парадокс Ябло вдохновил создание аналогичных парадоксов, содержащих не вполне фундированные нециклические структуры референции, также и в других предметных областях, кроме истины, таких как вариант парадокса Бранденбургера-Кейслера из теории эпистемических игр Башкента (Başkent 2016), версия, касающаяся доказуемости, Сиеслински и Урбаняка (Cieśliński and Urbaniak 2013) и версия в контексте теорем Гёделя о неполноте Лича-Кроуза (Leach-Krouse 2014).

2. В чем смысл парадоксов?

После того, как мы представили ряд парадоксов самореференции и обсудили некоторые основные сходства, мы можем перейти к обсуждению их значимости.

Значимость парадокса заключается в указании на недостаток или изъян в нашем обращении с основными понятиями, связанными с ним.

Похоже, в случае семантических парадоксов мы недостаточно хорошо знаем основные понятия семантики, таких как истина (в парадоксе лжеца и парадоксе Греллинга) или определимость (в парадоксах Берри и Ришара). В случае теоретико-множественных парадоксов речь идет о нашем знании понятия множества. Если бы мы знали эти понятия вдоль и поперек, то могли бы иметь с ними дело, не впадая в противоречия.

Как пример рассмотрим случай классического парадокса Зенона «Ахиллес и черепаха» (подробнее см. в статье о парадоксах Зенона). В этом парадоксе кажется возможным доказать, что черепаха может выиграть гонку с Ахиллесом, а он в десять раз быстрее ее, если дать ей сколь угодно малую фору. Зенон использовал этот парадокс в качестве довода против возможности движения. Позже выяснилось, что парадокс основывается на неадекватном понимании бесконечности. Точнее, он основывается на имплицитном допущении, что любой бесконечный ряд положительных вещественных чисел должен иметь бесконечную сумму. Более поздние разработки в математике бесконечных рядов показали, что это допущение ложно, вследствие чего парадокс был разрешен. Первоначальное принятие аргумента Зенона как парадокса указывает на недостаточное в то время знание понятия бесконечности. Поэтому резонно допустить, что существование семантических и теоретико-множественных парадоксов указывает на недостаточное знание нами соответствующих понятий семантики и теории множеств.

Другой возможный ответ состоит в том, что ошибочны наши представления о самом понятии «противоречие». Все рассуждения, связанные с парадоксами самореференции, содержат в конце некоторое противоречие — предложение, которое считается и истинным, и ложным. Мы считаем это невозможным, отсюда и парадокс, но, быть может, этого и не нужно делать? Диалетеизм — это точка зрения, согласно которой могут существовать «истинные противоречия», а значит, предложение вполне может быть истинным и ложным в одно и то же время. Если принять диалетеистскую точку зрения, парадоксы самореференции разрешаются и вместо этого превращаются в доказательства существования особой разновидности диалетеи. Прист (Priest 1987) — убежденный сторонник диалетеизма, который использует свой принцип единообразного решения (см. выше § 1.4) для его защиты. Дополнительные сведения см. в статьях о диалетеизме и параконсистентной логике.

В настоящее время не существует общепринятого решения парадоксов. Они продолжают служить источником фундаментальных проблем семантики и теории множеств. Нельзя притязать на прочные основания этих предметов, пока не будет найдено удовлетворительное решение для парадоксальных самореференций. Проблемы возникают в момент, когда дело доходит до формализации семантики (самого понятия истины) и теории множеств. Если формализовать интуитивное, наивное понимание предметов, противоречивые системы останутся на месте, поскольку в них будут формализованы и парадоксы.

2.1 Следствия семантических парадоксов

Парадокс лжеца — существенная помеха на пути построения формальных теорий истины, так как создает противоречия в потенциальных теориях. Значительное количество исследований в области самореференции сосредоточено на формальных теориях истины и способах обойти парадокс лжеца.

Больше, чем какие-либо другие, на работу над формальными теориями истины и парадоксом лжеца повлияли две статьи, а именно «Понятие истины в формализованных языках» Альфреда Тарского и «Наброски теории истины» Сола Крипке.

Сначала мы представим идеи из статьи Тарского (Tarski 1935) и ряд связанных с ними результатов. Статья Крипке (Kripke 1975) обсуждается в § 3.2.

Тарский выдвигает ряд условий, которым должно удовлетворять любое, по его словам, адекватное определение истины. Центральным является то из них, которое в наши дни чаще всего называют T-схемой (а также схемой T, или конвенцией T, или бикондиционалами Тарского):

(Т-схема) ϕ↔T⟨ϕ⟩ для всех предложений ϕ.

T — предикат, предназначенный для выражения истины, а ⟨ϕ⟩ — имя суждения ϕ. Применение предиката T к имени ⟨ϕ⟩ дает выражение T⟨ϕ⟩, предназначенное для репрезентации фразы «ϕ истинно». T-схема, таким образом, выражает, что для каждого ϕ, ϕ выполняется тогда и только тогда (т.т.т.), когда «ϕ истинно» имеет место. T-схема обычно понимается как множество предложений в рамках формальной теории. Здесь обычно принято использовать арифметику первого порядка, или логику предикатов первого порядка, расширенную множеством стандартных аксиом для арифметики, таких как PA (то есть арифметика Пеано) или Q Робинсона. Сказанное ниже применимо к любой такой формализации арифметики первого порядка. В этом случае ⟨ϕ⟩ выше обозначает код Гёделя ϕ, а T⟨ϕ⟩ — сокращение от T(⟨ϕ⟩). Читатель, незнакомый с нумерацией (или кодом) Гёделя, может просто считать ⟨⋅⟩ манерой именования или механизмом цитирования формул — чем-то вроде кавычек в естественном языке. Часто используемые варианты обозначения для ⟨ϕ⟩ — это ┌ϕ┐ и ‘ϕ’.

Тарский показал, что в любой формальной теории, содержащей T-схему, формализуем парадокс лжеца и, следовательно, любая такая теория должна быть противоречивой. Этот результат часто называют теоремой Тарского о неопределимости истины. По большей части это формализация парадокса лжеца в арифметике первого порядка, расширенной T-схемой. Чтобы построить эту формализацию, необходимо быть в состоянии формулировать самореференции (напр., предложение лжеца) в рамках первопорядковой арифметики. Подобное состояние обеспечивается диагональной леммой.

Диагональная лемма.

Пусть S — теория, расширяющая арифметику первого порядка. Для каждой формулы ϕ(x) существует суждение ψ такое, что S⊢ψ↔ϕ⟨ψ⟩.

Здесь нотация S⊢α обозначает, что α доказуемо в теории S, а ϕ⟨ψ⟩ — это сокращение от ϕ(⟨ψ⟩). Допустим, дана формула ϕ(x), предназначенная для выражения некоторого свойства суждений — например, истины. Тогда диагональная лемма дает существование суждения ψ, удовлетворяющего биимпликации ψ↔ϕ⟨ψ⟩. Суждение ϕ⟨ψ⟩ можно рассматривать как выражение того, что суждение ψ обладает свойством, выраженным ϕ(x). Таким образом, биимпликация выражает здесь то, что ψ эквивалентно предложению, выражающему, что ψ обладает свойством ϕ. Поэтому можно думать о ψ как о предложении, выражающем относительно себя, что оно само обладает свойством ϕ. В случае истины — это предложение, которое выражает относительно себя, что оно истинно. Предложение ψ, конечно, не самореферентно в строгом смысле, но математически ведет себя именно так. Поэтому предложения, порожденные диагональной леммой, можно использовать для формализации парадоксов, основанных на самореферентных предложениях, таких как парадокс лжеца. Диагональную лемму иногда называют леммой с неподвижной точкой, поскольку эквивалентность ψ↔ϕ⟨ψ⟩ можно рассматривать как выражение того, что ψ выступает неподвижной точкой ϕ(x).

Теория в логике предикатов первого порядка называется неконсистентной, если в рамках нее доказуемо логическое противоречие. Теорема Тарского (о неопределимости истины) теперь может быть сформулирована и доказана.

Теорема Тарского.

Любая теория, расширяющая арифметику первого порядка и содержащая схему T, противоречива.

Доказательство. Допустим, что существует консистентная формальная теория S, которая расширяет первопорядковую арифметику и содержит T-схему. Требуется показать, что такое допущение ведет к противоречию. Доказательство имитирует случай с парадоксом лжеца. Применим диагональную лемму для того, чтобы получить предложение λ, удовлетворяющее λ↔¬T⟨λ⟩ в S. Предложение λ выражает, что оно ложно само по себе, поэтому λ соответствует предложению лжеца. Подстановка T-схемы с предложением λ дает λ↔T⟨λ⟩. Теперь обе λ↔¬Т⟨λ⟩ и λ↔Т⟨λ⟩ имеют место в S (доказуемы в S), и таким образом Т⟨λ⟩↔¬Т⟨λ⟩ имеет место в S. Это противоречит консистентности S. □

Отметим: противоречие T⟨λ⟩↔T⟨λ⟩ выражает, что предложение лжеца истинно т.т.т., когда это не так. Сравним его с неформальным парадоксом лжеца, представленным в начале статьи. Теорема Тарского показывает, что в условиях арифметики первого порядка невозможно дать то, что Тарский называет «адекватной теорией истины».

Встает главный вопрос: как изменить (если это возможно) формализм или сами требования к адекватной теории истины таким образом, чтобы в итоге восстановить консистентность, то есть предотвратить тривиализацию системы парадоксом лжеца?

На этот вопрос есть много разных ответов, так как существует много разных способов восстановить консистентность. Наиболее влиятельные подходы мы рассмотрим ниже в § 3.

2.2 Следствия теоретико-множественных парадоксов

Парадоксы теории множеств бросают серьезный вызов основаниям математики. Они доказывают, что понятие множества не может удовлетворять принципу неограниченного выделения (также известного как принцип полного выделения или неограниченной абстракции):

Неограниченное выделение:

∀u(u∈{x∣ϕ(x)}↔ϕ(u)) для всех формул ϕ(x).

В неформальном контексте формулы ϕ(x) могли бы быть произвольными предикатами. В более формальном контексте они были бы формулами, например, подходящего языка первого порядка. Принцип неограниченного выделения гласит, что для любого свойства (выраженного ϕ) существует множество элементов, которые удовлетворяют свойству. Этот принцип кажется очень разумным, и он более-менее отражает интуитивное понятие множества. В самом деле, таково именно понятие множества, первоначально выдвинутое Георгом Кантором, самим отцом теории множеств (Cantor 1895). К сожалению, этот принцип не является обоснованным, поскольку он порождает парадокс Рассела. Рассмотрим свойство непринадлежности к себе. Оно может быть выражено формулой x∉x. Если ϕ(x) формула и x∉x, то множество {x∣ϕ(x)} станет множеством Рассела R, и мы получим следующую подстановку принципа неограниченного выделения:

∀u(u∈R↔u∉u).

Как и в рассуждении, связанном с парадоксом Рассела, к противоречию мы приходим, когда производим через R подстановку u:

R∈R↔R∉R.

Это противоречие выражает то, что множество Рассела есть элемент самого себя т.т.т., когда это не так. Тем самым было доказано следующее.

Теорема (Неконсистентность наивной теории множеств).

Любая теория, содержащая принцип неограниченного выделения, неконсистентна.

Сравним ее с теоремой Тарского. Та выражает, что при интуитивной формализации наиболее очевидного принципа истины в конечном итоге мы получаем неконсистентную теорию. Теорема выше показывает, что то же самое происходит при формализации интуитивно наиболее очевидного принципа, связанного с существованием множеств и принадлежностью.

Учитывая неконсистентность неограниченного выделения, задача заключается в поиске способа ограничить либо сам принцип выделения, либо лежащие в его основании логические принципы, чтобы восстановить консистентную теорию, то есть теорию множеств, которая не подвергнется тривиализации парадоксом Рассела. За последний век было разработано множество альтернативных теорий множеств, которые исключают принцип неограниченного выделения, в том числе теория типов Рассела и Уайтхеда, теория простых типов (ST), теория множеств Гёделя — Бернайса (GB), теория множеств Цермело — Френкеля (ZF) и новые основания Куайна (NF). Все они считаются консистентными, хотя простые доказательства их консистентности неизвестны. Все они, по крайней мере, избегают известных парадоксов самореференции. Мы вернемся к обсуждению этого в § 3.

2.3 Следствия эпистемических парадоксов

Эпистемические парадоксы представляют угрозу для построения формальных теорий познания, поскольку они формализуемы во многих таких теориях. Предположим, мы хотели бы построить формальную теорию познаваемости в рамках расширения арифметики первого порядка.

Для формализации выбирается познаваемость, а не познание, ведь знание всегда соотносится с некоторым агентом в определенный момент времени, тогда как познаваемость — всеобщее понятие, наподобие истины.

Можно было бы работать непосредственно со знаниями, но это потребовало бы больше усилий и сделало бы представление излишне сложным. Для того чтобы формализовать познаваемость, введем особый предикат K и используем предложения вида K⟨ϕ⟩ для выражения, что ϕ познаваемо. Как и в случаях с истиной и принадлежностью в теории множеств, должны существовать определенные логические принципы, которым К необходимо удовлетворять, чтобы формальная теория квалифицировалась как адекватная теория познаваемости. Прежде всего, все познаваемые предложения должны быть истинными. Это свойство можно формализовать с помощью следующего логического принципа:

• А1. K⟨ϕ⟩→ϕ для всех суждений ϕ.

Принцип сам по себе должен быть познаваемым, разумеется, поэтому мы также получаем принцип:

• А2. K⟨K⟨ϕ⟩→ϕ⟩ для всех суждений ϕ.

Кроме того, все теоремы арифметики первого порядка должны быть познаваемы:

• А3. K⟨ϕ⟩ для всех суждений ϕ арифметики первого порядка.

Кроме того, познаваемость должна быть замкнута в соответствии с логическими последствиями:

• А4. K⟨ϕ→ψ⟩→(K⟨ϕ⟩→K⟨ψ⟩) для всех суждений ϕ.

Итак, принципы А1–А4 — вот все, что требуется для формализации парадокса познающего. Точнее, благодаря Монтегю (Montague 1963) у нас имеется следующая теорема:

Теорема Монтегю.

Любая формальная теория, расширяющая арифметику первого порядка и содержащая схемы аксиом A1–A4, противоречива.

Доказательство. Допустим, что существует непротиворечивая формальная теория S, которая расширяет арифметику первого порядка и содержит схемы аксиом A1–A4. Нам требуется показать, что допущение такого рода приводит к противоречию. Доказательство имитирует сам ход парадокса познающего. Применим диагональную лемму для того, чтобы получить предложение λ, удовлетворяющее λ↔K⟨λ⟩ в S. Предложение λ выражает само по себе, что оно непознаваемо, поэтому λ примерно соответствует предложению познающего (ПП). Первая часть аргументации, использованная в парадоксе познающего, привела к выводу, что ПП действительно истинно. Этот фрагмент аргументации имитируется следующим отрывком формального рассуждения в рамках S:

Доказательство показывает, что λ — формальная версия ПП — доказуема в S. Оно соответствует неформальному аргументу об истинности ПП. Как утверждается в парадоксе познающего, любой агент, обладающий достаточными способностями к рассуждению, сможет доказать истинность ПП и, таким образом, узнать, что ПП имеет место. Таким образом, ПП должно быть познаваемо. В рамках рассматриваемого формального аппарата это значит, что мы можем доказать познаваемость λ в S:

Этим завершается доказательство познаваемости λ, соответствующее неформальному аргументу о познанности ПП тем или иным агентом. Обратите внимание на сходство доказательств в строках 1–7 и 8–14. Единственное отличие состоит в том, что в последнем случае всем формулам предшествует дополнительная буква K. Это связано с тем, что строки 8–14 выражают тот же ход рассуждений, что и строки 1–7, с той разницей, что последние являются доказательством познаваемости λ, а не истины λ. Придя к выводу, что λ одновременно истинно и познаваемо, мы теперь сразу получаем противоречие, как в парадоксе познающего:

Доказательство теоремы Монтегю завершено. □

Приведенное выше доказательство проще, чем исходное доказательство Монтегю (Montague 1963), и непосредственным образом имитирует ход рассуждений в случае парадокса познающего. Теорема Монтегю показывает, что в условиях арифметики первого порядка невозможна теория (по)знания или познаваемости, удовлетворяющая даже основным принципам A1–A4. Она обобщает теорему Тарского. Если символ предиката K удовлетворяет Т-схеме Тарского, то легко видеть, что он также будет удовлетворять схемам аксиом A1–A4. Итак, схемы аксиом A1–A4 представляют собой ослабление T-схемы, и теорема Монтегю показывает, что даже этой гораздо более слабой T-схемы достаточно для разрыва консистентности.

Формализация познания как предиката в логике первого порядка называется синтаксической трактовкой познания. В качестве альтернативы можно выбрать формализацию в виде модального оператора подходящей модальной логики. Такова семантическая трактовка. При семантической трактовке познания обычно избегают проблем самореференции, а значит, и неконсистентности, но за счет выразительной силы формализма, или ценой ее ослабления (проблемы самореференции исчезают в пропозициональной модальной логике, которая не допускает ничего вроде диагональной леммы для построения самореферентных формул).

Следствия относительно доказуемости и исчислимости

Главный аргумент, приведенный в доказательстве теоремы Тарского, тесно связан с аргументом в сердцевине первой теоремы Гёделя о неполноте (Gödel 1931). Теорему Гёделя сформулируем так.

Теория называется ω-консистентной, если для любой формулы ϕ(х), содержащей x в качестве единственной свободной переменной, справедливо следующее: если ⊢¬ϕ(n) для любого натурального n, то ⊬∃xϕ(х). ω-консистентность сильнее, нежели просто консистентность, поэтому любая ω-консистентная теория консистентна. Теория неполна, если содержит формулу, которую нельзя ни доказать, ни опровергнуть.

Эскиз доказательства первой теоремы Гёделя о неполноте. Допустим, что арифметика первого порядка одновременно ω-консистентная и полная. Нам нужно показать, что это допущение приводит к противоречию. Гёдель строит формулу Bew (от Beweis ‘доказуемый’) в формальной арифметике, удовлетворяющую для всех ϕ и всех n

• (1) ⊢Bew(n,⟨ϕ⟩) т.т.т., когда n — гёделев номер доказательства ϕ.

Допуская, что теория ω-консистентна и полна, мы можем доказать, что для всех суждений ϕ

• (2) ⊢∃xBew(x,⟨ϕ⟩) т.т.т., когда ⊢ϕ.

Доказательство (2) выглядит следующим образом. Сначала мы докажем импликацию слева направо. Если ⊢∃xBew(x,⟨ϕ⟩), то существует такое n, что ⊬Bew(n,⟨ϕ⟩), по ω-консистентности. По полноте мы получаем ⊢Bew(n,⟨ϕ⟩) для n. Из (1) выше мы получаем, что n обозначает доказательство ϕ. То есть ϕ доказуемо, поэтому у нас есть ⊢ϕ. Чтобы доказать импликацию справа налево, заметим, что если ⊢ϕ, должно быть такое n, что ⊢ Bew(n,⟨ϕ⟩), по (1). Отсюда мы получаем ⊢∃x Bew(x,⟨ϕ⟩), как и требуется. На этом (2) доказано. Теперь, когда в полной теории у нас есть (2), также получается:

• (3) ⊢∃xBew(x,⟨ϕ⟩)↔ϕ для всех суждений ϕ.

Если мы сократим ∃xBew(x,⟨ϕ⟩) до T⟨ϕ⟩, то (3) принимает вид:

⊢T⟨ϕ⟩↔ϕ для всех суждений ϕ.

Это и есть Т-схема! Таким образом, если мы предположим, что арифметика первого порядка ω-консистентна и полна, то в ней интерпретируема T-схема. Итак, теорема Тарского показывает, что подобной консистентной теории не существует, и, таким образом, мы приходим к противоречию. □

В приведенном доказательстве мы свели, для того чтобы показать их тесную связь, теорему Гёделя о неполноте к применению теоремы Тарского (эта версия доказательства взята из Bolander 2002). Гёдель хорошо знал об их связи, и действительно, похоже, что он даже доказал теорему Тарского до того, как это сделал сам Тарский (Feferman 1984). Теорему Гёделя можно интерпретировать как демонстрацию ограничения того, что может быть достигнуто с помощью чисто формальных процедур. В ней говорится, что если арифметика первого порядка ω-консистентна (как считается), в ней должны существовать предложения, которые не могут быть ни доказаны, ни опровергнуты формальными процедурами арифметики первого порядка. Сначала можно было ожидать, что это ограничение разрешимо путем включения дополнительных аксиом, но Гёдель показал, что неполнота все еще имеет место, когда арифметика первого порядка расширяется произвольным конечным множеством схем аксиом (или, в более общем понимании, произвольным рекурсивным множеством аксиом). Итак, мы получаем общий результат ограничения, и как таковой он говорит о невозможности формально доказать истинность или ложность любого арифметического суждения (несуществовании соответствующей процедуры). Более подробное обсуждение теоремы Гёделя о неполноте см. в статье о Курте Гёделе.

Результат ограничения теоремы Гёделя тесно связан еще с одним результатом ограничения, который касается ограничений вычислимости и известен под именем неразрешимости проблемы остановки. Мы представим его ниже. Он основан на понятии машины Тьюринга, представляющей собой общую модель программы, работающей на компьютере с неограниченной памятью. Любую программу, запущенную на любом компьютере, можно рассматривать как машину Тьюринга (см. статью о машинах Тьюринга). Машина Тьюринга после запуска либо завершится после конечного числа шагов вычисления, либо будет работать вечно. В первом случае мы говорим, что она останавливается. Проблема остановки касается поиска машины Тьюринга, которая может решить, останавливаются другие машины Тьюринга или нет. Машина Тьюринга H разрешает проблему остановки, если выполняется следующее:

H принимает на вводе (в качестве входных данных) пару (⟨A⟩,x) из гёделева номера ⟨A⟩ машины Тьюринга A и произвольной строки x. H возвращает ответ «да», если машина Тьюринга A останавливается при вводе x, и «нет» в противном случае.

Если машина Тьюринга H разрешает проблему остановки, ее можно применить для произвольных машины Тьюринга A и ввода x вне зависимости от того, останавливается ли A на вводе x или нет. Неразрешимость проблемы остановки — это результат, полученный Тьюрингом (Turing 1937) и гласящий, что такой машины не может быть:

Доказательство. Допустим, существует машина Тьюринга, решающая проблему остановки. Нам нужно показать, что такое допущение приводит к противоречию. Доказательство имитирует ход парадокса Греллинга. Назовем машину Тьюринга гетерологичной, если A не останавливается на вводе ⟨A⟩, то есть когда вводится ее собственный код Гёделя. Используя H, мы построим машину Тьюринга G, которая останавливается т.т.т., когда в качестве входных данных ей задан код Гёделя гетерологичной машины Тьюринга. G работает в таком режиме:

G принимает в качестве ввода (входных данных) код Гёделя машины Тьюринга A. Затем она запускает H на входе (⟨A⟩,⟨A⟩). Если H на вводе (⟨A⟩,⟨A⟩) возвращает «нет», мы знаем, что A гетерологично, а G остановилась. Если, с другой стороны, H на вводе (⟨A⟩,⟨A⟩) возвращает «да», то G начинает бесконечный цикл (вынуждена никогда не останавливаться).

По аналогии с парадоксом Греллинга теперь мы можем спросить, является ли G гетерологичной машиной Тьюринга или нет. В итоге мы получаем следующий ряд эквивалентностей:

Тем самым выходит и требуемое противоречие. □

Из двух вышеприведенных теорем мы видим, что в областях доказуемости и вычислимости парадоксы самореференции превращаются в результаты ограничения (limitation results): существуют пределы того, что можно доказать и что доступно для вычисления. На самом деле это очень похоже на то, что произошло в областях семантики, теории множеств и эпистемологии: парадоксы самореференции стали теоремами, которые показывают, что существуют пределы, в которых можно консистентно допускать наличие таких-то и таких-то свойств у предиката истины (теорема Тарского), у теории множеств в целом (неконсистентность наивной теории множеств) и у предиката познания (теорема Монтегю).

Все же мы вынуждены принять ограничения и признать тот факт, что в этих областях нам нельзя получить все, о чем (в противном случае) разумно было бы желать.

Разрешение парадоксов

В данном разделе рассматривается, как разрешить парадоксы — или по меньшей мере обойти. Чтобы разрешить или обойти парадокс, нужно ослабить некоторые допущения, ведущие к противоречию. Выбрать, какие именно из допущений следовало бы ослабить, крайне трудно, поскольку каждое из эксплицитных предположений, лежащих в основе парадокса, представляется «очевидно истинным» — в противном случае парадокс не имел бы статус парадокса. Ниже будут рассматриваться наиболее влиятельные подходы к разрешению парадоксов.

До сих пор повествование структурировалось в соответствии с разновидностью парадокса, то есть семантические, теоретико-множественные и эпистемические парадоксы рассматривались по отдельности. Но мы также показали, что эти три типа схожи по своей структуре, и утверждали, что решение парадокса одного типа должно сработать и для остальных (по принципу единообразного решения). Далее изложение структурируется не по типу парадокса, а по типу решения. Каждый тип решения, рассмотренный ниже, можно применить к любому из парадоксов самореференции, хотя в большинстве случаев разбираемые построения изначально разрабатывались с учетом одного из типов парадокса, а не всех сразу.

Построение эксплицитных иерархий

Построение иерархий — это метод обхода как и теоретико-множественных, так и семантических и эпистемических парадоксов. Изначально парадокс Рассела и проблема неопределенности истины Тарского разрешались построением иерархии. В первом случае Рассел предложил теорию типов. Во втором случае Тарский дал то, что в наши дни известно как иерархия языков Тарского. В обоих случаях идея состояла в том, чтобы подвергнуть вселенную дискурса (множества, предложения) стратификации — разбить ее на уровни. В теории типов уровни — это типы. Фундаментальная идея теории состоит в том, чтобы ввести ограничение, согласно которому любое множество некоторого типа может содержать исключительно элементы более низких типов (лишь те множества, которые расположены ниже в иерархии). Оно действенно блокирует парадокс Рассела, поскольку в таком случае ни одно множество попросту не может быть элементом самого себя.

В случае Тарского стратификация выглядит так. Предположим, что некто хочет снабдить язык L0 предикатом истинности. Из теоремы Тарского (§ 2.1) известно, что этот предикат не может входить в состав самого языка L0 — по крайней мере пока мы хотим, чтобы предикат удовлетворял T-схеме. Вместо этого строится иерархия языков — L0, L1, L2, …, где в каждом языке Li+1 имеется предикат истинности Ti+1, который применяется только к суждениям Lj, j≤i. В этой иерархии L0 называется объектным языком, а метаязыком Li для всех i становится Li+1. Иерархия действенно блокирует парадокс лжеца, поскольку с момента ее введения суждение может выражать только истинность или ложность суждений на более низких уровнях, и, следовательно, такое суждение, как предложение лжеца, которое выражает собственную неистину, нельзя сформулировать.

Теорию типов Рассела можно рассматривать как разрешение парадокса Рассела, поскольку в ней показано, как именно можно «починить» теорию множеств с тем, чтобы он исчез. Схожим образом иерархию Тарского можно считать разрешением парадокса лжеца.

Следует отметить, что парадокс Рассела и парадокс лжеца в решающей степени зависят от понятий (самопринадлежности, самореференции), которые предполагают цикличность. Цикличность исчезает, когда введена стратификация, в которой объект может содержать в себе или же упоминать только объекты более низких уровней. В случае эпистемических парадоксов это достигается путем эксплицитного различения знаний первого порядка (о внешнем мире), второго порядка (о знаниях первого порядка), третьего порядка (о знаниях второго порядка) и т.д. Стратификация подобного рода автоматически производится при семантической трактовке, формализующей знание в виде модального оператора.

Построения эксплицитных иерархий достаточно, чтобы избежать цикличности, а следовательно, и стандартных парадоксов самореференции. Однако существуют и парадоксы наподобие парадокса Ябло, которые не полагаются на цикличность и самореференцию. От них также можно укрыться с помощью иерархического подхода, но в таком случае необходимо дополнительное требование полной фундированности иерархии — чтобы в ней обозначался самый низкий уровень. В противном случае все еще можно сформулировать «не вполне фундированные» парадоксы. Парадокс Ябло можно формализовать в нисходящей иерархии языков. Нисходящая иерархия языков состоит из языков L0, L−1, L−2, …, где в каждом языке L−i имеется предикат истинности, применимый только лишь к предложениям языков L−j, j>i. И точно так же теоретико-множественный парадокс неполной фундированности можно сформулировать в теории типов, допускающей отрицательные типы. Вывод отсюда следует такой: стратификации вселенной самой по себе недостаточно, чтобы избежать всех парадоксов, — стратификация также должна быть вполне фундированной.

Большинство авторов построение эксплицитной (вполне фундированной) иерархии для решения парадоксов ныне считает чересчур радикальным и жестким подходом. Иерархии вводят ряд сугубо технических деталей, усложняющих ситуацию и отсутствующих в «плоской вселенной», и пускай парадоксы действительно исчезают, то же самое происходит и со всеми случаями самореференции — в том числе и не парадоксальными. Крипке (Kripke 1975) приводит следующий пример из обыденного дискурса. Пусть N — это следующее утверждение Никсона:

• (N) Все высказывания Джонса об Уотергейте истинны,

— и пусть J будет следующим утверждением Джонса:

• (J) Большинство высказываний Никсона об Уотергейте ложны.

В иерархии языка по Тарскому предложение N должно находиться на более высоком уровне, чем все высказывания Джонса, тогда как предложение J, наоборот, должно находиться на более высоком уровне, чем все высказывания Никсона. Так как N — высказывание Никсона, а J — высказывание Джонса, N должно было бы находиться на более высоком уровне, чем J, а J — на более высоком уровне, чем N. Очевидно, что это невозможно, а потому в иерархии вроде иерархии Тарского такие предложения нельзя даже сформулировать. N и J действительно косвенно самореферентны, так как N ссылается на тотальность, включающую J, а J ссылается на тотальность, включающую N. Тем не менее в большинстве случаев N и J безвредны и не создают парадокса. Парадокс возникает только в особом случае, когда все высказывания Джонса, за исключением, возможно, J, истинны, и ровно одна вторая всех высказываний Никсона ложна, кроме N. Только в определенном частном случае Крипке пользуется фактом проблематичности N и J как доводом против того подхода, который полностью исключает возможность формулирования N и J.

Еще один довод против иерархического подхода состоит в том, что эксплицитная стратификация не входит в состав обыденного дискурса, поэтому можно считать ее введение в формальные условия с одной лишь целью обойти парадоксы несколько ad hoc.

Приведенные аргументы — одна из причин, по которой работы Рассела и Тарского не считались работами, где были предоставлены окончательные решения парадоксов. Были предложены мириады альтернативных решений. Так, можно попытаться найти имплицитные, а не эксплицитные иерархии. Имплицитной является иерархия, эксплицитно не отраженная в синтаксисе языка. В следующем разделе мы рассмотрим некоторые из решений парадоксов, полученных с помощью подобных имплицитных стратификаций.

Построение имплицитных иерархий

Иерархический подход Тарского к семантическим парадоксам доминировал в области до 1975 года, пока Крипке не опубликовал свой знаменитый и чрезвычайно влиятельный «Набросок теории истины». Эта статья в значительной степени сформировала большинство более поздних подходов к теориям истины и семантическим парадоксам. Однако следует отметить, что идеи, весьма схожие с идеями Крипке, одновременно и независимо от него разрабатывались Мартином и Вудраффом (Martin and Woodruff 1975) и что в рамках теории множеств аналогичный подход был независимо разработан Гилмором (Gilmore 1974).

Теория истины Крипке

Идеи Крипке опираются на анализ проблем, связанных с иерархическим подходом Тарского. Крипке перечисляет ряд аргументов против языковой иерархии, в которой каждое предложение находится на неподвижном уровне, определяемом его синтаксической формой. Он предлагает альтернативное решение, в котором все еще используется идея наличия уровней, но при этом уровни не входят в эксплицитный состав синтаксиса. Скорее, уровни становятся этапами в итеративном построении предиката истинности. Чтобы объяснить конструкцию Крипке, требуется некоторый дополнительный аппарат.

На каждом этапе построения Крипке предикат истинности лишь частично определен, то есть он применим только к некоторым предложениям языка. Для работы с частично определенными предикатами используется трехзначная логика, то есть логика, оперирующая третьим значением истинности — не определено — в дополнение к привычным истина и ложь. Часто его обозначают как «u» (от ориг. англ. undefined) или «⊥» (снизу). Когда частично определенный предикат применен к одному из терминов, для которых был определен предикат, он получит только одно из классических значений истинности, истина или ложь, тогда как в противном случае — не определено. Существует несколько трехзначных логик, различающихся по тому, как обрабатывается третье значение. Здесь кратко описана только одна из них, называемая сильной трехзначной логикой Клини. Подробные сведения об этой и связанных с ней логиках см. в статье о многозначной логике.

В сильной трехзначной логике Клини значение ⊥ (не определено) может быть интерпретировано как «еще не определено». Таким образом, формулы со значением ⊥ могут быть поняты как формулы, на самом деле имеющие классическое значение (будь то истина или же ложь), которое просто еще не определено. Такая интерпретация «не определено» отражена в таблицах истинности ниже. Верхняя таблица истинности дана для дизъюнкции, нижняя — для отрицания:

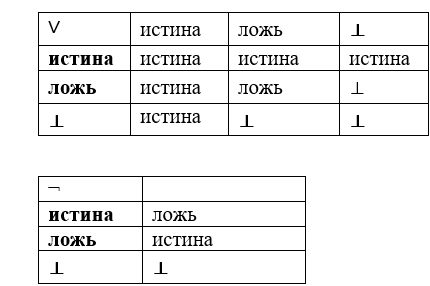
Эти таблицы истинности полностью определяют трехзначную логику, так как ∨ и ¬ используются для формирования адекватного множества связок, а квантификации по существованию и общности рассматриваются как бесконечная дизъюнкция и конъюнкция соответственно.

Для обработки частично определенных предикатов истинности необходимо ввести понятие частичных моделей. В частичной модели для языка первого порядка каждый символ n-местного предиката P интерпретируется парой непересекающихся n-местных отношений на домене модели (U,V). U называется объемом P, а V — его анти-объемом (anti-extension). В данной модели P истинен для объектов в U, ложен для объектов в V и не определен в противном случае. Любое атомарное предложение получает в модели одно из значений истинности: истина, ложь или не определено. Неатомарным формулам в модели значения истинности присваиваются благодаря использованию сильной трехзначной логики Клини для оценки связок.

Учитывая определение частичной модели, частично интерпретируемый язык представляет собой пару (L,M), где L — язык первого порядка, а M — частичная модель L. Крипке рекурсивно задает ряд частично интерпретируемых языков L0, L1, L2, …, отличающихся только интерпретацией предиката истинности T. Первый язык — L0 — принимается за произвольный язык, в котором как объем, так и анти-объем T — пустые множества. Стало быть, в L0 предикат истинности полностью не определен. Для любого α язык Lα+1 подобен Lα, за исключением того, что T интерпретируется парой объема/анти-объема (U,V), заданной:

• U — множеством гёделевых номеров ⟨ϕ⟩ предложений ϕ, истинных в Lα.

• V — множеством гёделевых номеров ⟨ϕ⟩ предложений ϕ, ложных в Lα.

Это определение сразу позволяет нам вывести, что для всех α

• (4) ϕ истинно (ложно) в Lα ⇔ T⟨ϕ⟩ истинно (ложно) в L α+1.

В итоге был построен ряд L0, L1, L2, … частично интерпретируемых языков, где T интерпретируем в Lα+1 в виде предиката истинности для Lα.

Ряд L0, L1, L2, … обладает важным свойством: для каждого α интерпретация T в Lα+1 расширяет (extends) интерпретацию T в Lα, то есть и объем, и анти-объем T растут (или остаются неизменными) при переходе от Lα к Lα+1. А стало быть, можно определить новый, частично интерпретируемый язык Lω, позволив объему T быть объединением всех объемов T в L0, L1, L2,...; и аналогично для анти-объема. Таким образом, в Lω интерпретация T расширяет интерпретацию, которую T получает во всех предыдущих языках. Это дает стратегию переноса итерационного построения предиката истины в трансфинитную область:

Для каждого ординала следования α+1 определим Lα+1 от Lα так же, как и в конечном случае выше; и для каждого предельного ординала σ определим Lσ от предшествующих языков (Li)i<σ точно так же, как и определено Lω (подробное объяснение роли порядковых чисел и их использования в этом контексте см. в статье о ревизионной теории истины). Простое рассмотрение кардинальности теперь показывает, что этот трансфинитный ряд языков в итоге будет стабилизирован: существует такой ординал γ, что Lγ=Lγ+1. Значит, получается следующая подстановка (4):

• (5) ϕ истинно (ложно) в Lγ ⇔ T⟨ϕ⟩ истинно (ложно) в Lγ.

Это показывает, что Lγ на деле является языком, содержащим собственный предикат истинности: любое предложение ϕ истинно (ложно) т.т.т., когда предложение, выражающее его истинность, T⟨ϕ⟩, истинно (ложно). Эквивалентность (5) есть не что иное, как семантический аналог T-схемы Тарского в трехзначной логике. Построение языка Lγ было одним из основных вкладов Крипке (Kripke 1975). Оно показывает, что в трехзначном формализме язык действительно может содержать собственный предикат истинности. Легко увидеть, что третье значение, не определено, оказывается важным для того, чтобы все работало: если бы Lγ был полностью интерпретированным языком (без неопределенных суждений), то Lγ удовлетворял бы схеме T, согласно (5) выше. Однако это противоречит теореме Тарского о возможности такого языка.

Среди предложений, которые получают значение не определено в Lγ, есть и предложение лжеца. Решение парадокса лжеца, подразумеваемого в теории Крипке, заключается в следующем: поскольку и допущение, что предложение лжеца истинно, и допущение, что оно ложно, приводят к противоречию, предложение лжеца будет ни тем, ни другим, то есть оно не определено. Говорят, что предложение лжеца страдает от истинностного провала. Идея избежать парадокса лжеца за счет истинностного провала действительно несколько раз появлялась в литературе до статьи Крипке, но Крипке был в числе первых, кто сделал эту идею неотъемлемой частью отдельной теории.

Ядро критики состоит в том, что использование трехзначной семантики дает интерпретируемый язык, очень слабый в выразительном отношении. Например, ни в одном из языков Крипке не может быть предиката, выражающего свойство быть со значением истинности не определено. На самом деле это отмечает и сам Крипке. Если бы частично интерпретируемый язык содержал такой предикат, в нем можно было бы сформулировать усиленное предложение лжеца «Это суждение либо ложно, либо не определено». Усиленное предложение лжеца истинно т.т.т., когда ложно или не определено, поэтому у нас есть новый парадокс усиленного лжеца. Трудность с ним известна под именем реванш-проблемы: похоже, что при любом решении парадокса лжеца мы можем придумать новый — схожий, однако усиленный — парадокс, остающийся нерешенным. Идея состоит в том, что вне зависимости от того, каким семантическим статусом, по предполагаемому решению, обладает предложение лжеца, возможно создать новый парадокс, если только будет разрешено свободно ссылаться на семантический статус на объектном языке.

Неспособность языка Крипке выразить свой предикат не определено также означает, что мы не можем на объектном языке Крипке выразить такое утверждение, как «Предложение лжеца не определено». На самом деле в языке Крипке Lγ предложение лжеца не определено, вследствие чего предыдущее предложение выражает истину о Lγ, которая не может быть выражена в самом Lγ (стало быть, язык выразительно неполон). Чтобы выразить истинное утверждение «Предложение лжеца не определено», мы вынуждены подняться на метаязык Lγ. Как выразился сам Крипке (Kripke 1975): «Призрак иерархии Тарского все еще с нами».

Расширения и альтернативы теории истины Крипке

Вслед за работой Крипке было предпринято много попыток выстроить языки, содержащие свой предикат истины и не подверженные угрозе со стороны реванш-проблемы усиленного парадокса лжеца. Многие такие попытки сосредотачивались на изменении или расширении лежащей в основе сильной трехзначной логики, напр., на изменении семантики кондиционалов (Field 2003, 2008) или на допущении неограниченного числа значений истинности (Cook 2007, Schlenker 2010, Tourville and Cook 2016).

Теория Крипке предотвращает парадокс лжеца, присваивая ему значение не определено. Тогда альтернативный способ избежать парадокса лжеца — это присвоить ему значение и истина, и ложь в подходящей параконсистентной логике. Согласно диалетеистской точке зрения, именно это решение было бы верным (см. § 2). Одна из простейших параконсистентных логик, LP представляет собой трехзначную логику с теми же таблицами истинности, что и представленная выше сильная трехзначная логика Клини. Единственное отличие заключается в том, что третье значение трактуется как «и истина, и ложь», а не как «не определено». Причина, по которой параконсистентная логика предпочтительнее частичной, состоит в том, что парадоксальные суждения, такие как парадокс лжеца, можно смоделировать в виде истинных противоречий — диалетей, а не в виде провалов истинности. Подробнее об этом см. в статьях о диалетеизме и параконсистентной логике.

Выбор стоит между истинностным провалом и пресыщенной оценкой: истинностный провал — это утверждение без значения истинности, будь то истина или ложь (как «не определено» в сильной трехзначной логике Клини), а вот пресыщенная оценка — утверждение с несколькими значениями истинности, например, одновременно истина и ложь (как в параконсистентной логике LP). Есть аргументы в пользу допущения как провала, так и пресыщения; в рамках таких решений множество значений истинности формирует двустороннюю систему (Fitting 2006, Odintsov and Wansing 2015). Простейшая нетривиальная бирешетка имеет ровно четыре значения, которые в истинностном контексте интерпретируются как истина, ложь, ⊥ (ни истина, ни ложь) и ⊤ (и истина, и ложь).

Более подробное обсуждение теории Крипке, ее последователей и соперников см. в статье о парадоксе лжеца.

Имплицитные иерархии в теориях множеств

Идея построения имплицитных, не эксплицитных иерархий использовалась и в теории множеств. Новые основания (NF) Куайна (Quine 1937) — это модификация простой теории типов, в которой стратификация на синтаксические типы заменена стратификацией по принципу выделения:

Выделение в логике НО:

∀u(u∈{x∣ϕ(x)}↔ϕ(u)), для всех стратифицированных формул ϕ(x).

Формула ϕ стратифицирована, если существует такое отображение σ (стратификация) исходя из переменных ϕ на натуральные числа, что если u∈v — подформула ϕ, тогда σ(v)=σ(u)+1, а если u=v — подформула ϕ, тогда σ(v)=σ(u). Очевидно, что формула x∉x не стратифицирована, и поэтому принцип выделения NF не может использоваться для формулировки в теории парадокса Рассела. Новые основания Куайна, по сути, получены из теории типов путем сокрытия типов из синтаксиса. Таким образом, теория по-прежнему использует иерархический подход для избегания парадоксов, но иерархия уже не эксплицитна, то есть она не представлена в синтаксисе формул. Кантини (Cantini 2015) исследовал возможность имитации этого неэксплицитного иерархического подхода в контексте теорий истины (в итоге она дает имплицитно репрезентированную иерархию истин по Тарскому).

Теория множеств Цермело — Френкеля (ZF) — еще одна теория, которая основана на идее неэксплицитной иерархии, позволяющей обойти парадоксы. Однако делает она это гораздо менее непосредственно, нежели чем NF. В ZF множества строятся снизу вверх — начиная с пустого множества и итерируя построение все больших и больших множеств с использованием операций объединения и вывода степенного множества. Так создается иерархия с пустым множеством самого низкого уровня 0 и операцией вывода степенного множества, создающей множество уровня α+1 из множества уровня α. Как и в итерациях Крипке, процедура переносится в область трансфинитного путем использования оператора объединения на предельных ординальных уровнях. Полученная иерархия называется совокупной иерархией. Одна из аксиом ZF — аксиома основания — гласит, что каждое множество ZF существует на некотором уровне в этой иерархии. Иными словами, в ZF нет множеств помимо тех, что могут быть построены снизу вверх с помощью описанной итерационной процедуры. Поскольку в совокупной иерархии не может быть множеств, содержащих самих себя, нет универсальных или не вполне фундированных множеств, то ни один из известных парадоксов не может быть немедленно сформулирован в теории. Очевидно, что само по себе это не обеспечивает консистентности ZF, но по меньшей мере видно, что идея иерархии множеств играет важную роль и в ZF. ZF имеет привилегированный статус среди теорий множеств, поскольку это наиболее широко признанный на данный момент кандидат на роль формального основания математики.

Общие подходы с неподвижной точкой

Представленное выше итеративное построение Крипке предиката истинности можно понимать как пример более общего подхода с неподвижной точкой к построению формальных теорий истины. Подходы с неподвижной точкой играют ключевую роль в современных формализациях истины. Основная идея заключается в том, чтобы получить оператор ревизии истинности, а затем обнаружить неподвижные точки этого оператора. В основе подходов с неподвижной точкой лежит некоторая релевантная теорема о неподвижной точке, которая бы гарантировала существование неподвижных точек для особых типов операторов. В доступе имеется много теорем о неподвижной точке. Давайте рассмотрим один из более простых вариантов.

Теорема о неподвижной точке.

Пусть τ — монотонный оператор в полной цепи частичного порядка (chain complete partial order, далее — ccpo). Тогда τ имеет наименьшую неподвижную точку, то есть существует такое наименьшее f, что τ(f)=f.

И ccpo — это частичный порядок (D,<), в котором каждое полностью упорядоченное подмножество D имеет по меньшей мере верхнюю границу. Полностью упорядоченные подмножества D называются цепями в D. Монотонный оператор (D,<) — отображение τ:D→D, удовлетворяющее:

d1≤d2⇒τ(d1)≤τ(d2) для всех d1,d2∈D.

Конструкция Крипке вписывается в приведенную выше теорему о неподвижной точке следующим образом. Во-первых, отметим, что множество частично интерпретируемых языков, которые различаются только по интерпретации Т, образует ccpo:

Попросту определим упорядочивание этих языков по L1≤L2 т.т.т., когда интерпретация T в L2 расширяет интерпретацию Tв L1 (т.е. и объем, и анти-объем T в L1 включены в объем и анти-объем L2). Затем зададим оператор ревизии истинности τ на этих языках с помощью:

• (6) τ(L)=L', где T⟨ϕ⟩ истинно (ложно) в L', т.т.т., когда ϕ истинно (ложно) в L.

Обратите внимание, что если Lα — один из языков в построении Крипке, то Lα+1=τ(Lα). Идея этого оператора ревизии истинности τ состоит в том, что если τ(L)=L', то L' будет языком, в котором T интерпретируется как предикат истинности для L. Следовательно, если τ(L)=L для некоторого L, т.е. L — неподвижная точка τ, то L будет языком, содержащим собственный предикат истинности. Этим мотивируется поиск неподвижных точек τ. Поскольку легко увидеть, что τ монотонный, то, согласно теореме о неподвижной точке, он имеет наименьшую такую точку. Нетрудно заметить, что она точно соответствует языку Lγ, построенному в теории истины Крипке. Так, построение Крипке восстанавливается путем установки неподвижных точек для монотонных операторов.

Смысл введения дополнительного механизма не только в том, чтобы заново открыть язык Lγ. Дело скорее в том, чтобы предоставить гораздо более общее и абстрактное основание, которое может привести к новым теориям истины и обогатить будущее понимание семантических парадоксов. Оказывается, что оператор ревизии истинности τ, определенный выше, имеет много интересных неподвижных точек помимо Lγ. Также возможно получить новые теории истины, рассмотрев альтернативные способы превращения множества интерпретируемых языков в ccpo. К примеру, можно добавить еще одно значение истинности и рассмотреть ситуацию в четырехзначной логике, как было предложено в Fitting 1997; или можно убрать третье значение не определено и построить ccpo уже в полностью классическом формализме. В последнем внимание ограничится полностью интерпретированными языками (где предложение всегда либо истина, либо ложь), упорядочивание в которых задается по формуле: L1≤L2 имеет место т.т.т., когда объем предиката истинности в L1 включен в объем предиката истинности в L2, т.е. т.т.т., когда L2 указывает на истинность того же как минимум числа предложений, что L1. Это дает ccpo. Используя теорему о неподвижной точке для подходящего оператора ревизии, довольно легко доказать существование в рамках такого аппарата полностью интерпретированного языка, который содержит положительное определение истины. Подразумевается, что интерпретированный язык имеет предикат T, который удовлетворяет следующей ограниченной версии T-схемы:

• (7) ϕ↔T(⟨ϕ⟩) для всех положительных предложений ϕ,

где положительными называются предложения, построенные без использования отрицания (¬). Поскольку (7) удовлетворяется в полностью интерпретированном языке, теория первого порядка, содержащая предложения из (7) в роли аксиом, должна быть консистентной. Результат такого толка следует противопоставить теореме Тарского, утверждающей, что неограниченная T-схема неконсистентна. Если принцип неограниченного выделения сходным образом ограничивается положительными формулами, мы также получаем консистентную теорию. Впервые это было показано Гилмором (Gilmore 1974).

Подход с неподвижной точкой — еще и отправная точка ревизионной теории истины, разработанной Белнапом и Гуптой (Belnap and Gupta 1993). Среди разработанных со времен Крипке теорий истины и семантических парадоксов она является самой влиятельной. Ревизионная теория истины рассматривает стандартный оператор ревизии истины τ, определенный в (6), как оператор в полностью интерпретированных языках. На этих языках τ не имеет неподвижной точки: если бы у него была такая неподвижная точка L, то L был бы полностью интерпретированным языком, удовлетворяющим полной T-схеме, что прямо противоречит теореме Тарского. Поскольку τ не имеет неподвижной точки в полностью интерпретированных языках, вместо этого теория ревизии рассматривает бесконечные ряды L1, L2, …, Lω, Lω+1, … полностью интерпретированных языков, удовлетворяющих:

• Для любого ординала следования α+1, L α+1=τ(L α).

• Для любого предельного ординала σ и любого предложения ϕ, если ϕ стабилизируется на значении истина (ложь) в ряду (L α)α<σ, то ϕ истинно (ложно) в Lσ.

В таком ряде каждое предложение ϕ в конечном итоге либо стабилизируется на классическом значении (истинно или ложно), либо никогда не стабилизируется. Пример второго варианта дает предложение лжеца: если предложение лжеца истинно в одном из языков L α, оно будет ложным в Lα+1, и наоборот.

В ревизионной теории, как утверждается, формулируется более правильное представление об истине и самореференции, чем теория Крипке, в которой предложению лжеца попросту присваивается значение не определено. И ревизионная теория, и теории с неподвижной точкой на манер Крипке по-прежнему активно исследуются (Gupta and Standefer 2017, Hsiung 2017, Schindler 2017). Полный разбор см. в статье о ревизионной теории истины.

Изучение самореферентных явлений в качестве неподвижных точек не ограничивается теориями истины. В контексте эпистемических парадоксов, к примеру, парадокс Бранденбургера — Кейслера был представлен в виде результата с неподвижной точкой в работе Abramsky and Zvesper 2015.

Новые подходы

Мурци и Массимилиано (Murzi and Massimiliano 2015) дают обзор последних подходов к решению парадоксов, таких как паракомплектность (где допускаются провалы в значениях истинности), параконсистентность (где последние пресыщены), субструктурная логика (где ослаблены принципы классической логики), и рассматривают проблемы реванша (revenge problems), к которым приводят или могут привести эти подходы. К последним разработкам в области субструктурной логики как «лекарства от парадоксов» можно отнести работы French 2016 с запретом на рефлексивность, Caret, Colin and Weber 2015, Shapiro and Lionel 2015, Mares and Paoli 2014 с отказом от сокращения и Cobreros, Égré, Ripley and van Rooij 2014 с отказом от транзитивности. В сборнике Achourioti et al. (eds) 2015 ряд статей посвящен самореференции и тому, как избежать парадоксов в контексте теорий истины.

Фолькер Хальбах и Альберт Виссер (Halbach and Visser 2014a, 2014b) провели довольно подробное исследование самореференции в арифметике. Они изучали, что означает приписывать себе свойства для арифметического суждения и как это зависит от выбранной кодировки, деталей построений с неподвижной точкой и т.п.

Библиография

● Abad, Jordi Valor, 2008, “The inclosure scheme and the solution to the paradoxes of self-reference”, Synthese, 160(2): 183–202.

● Abramsky, Samson, and Jonathan Zvesper, 2015, “From Lawvere to Brandenburger-Keisler: Interactive forms of diagonalization and self-reference”, Journal of Computer and System Sciences, 81(5): 799–812.

● Achourioti, T. et al. (eds.), 2015, Unifying the Philosophy of Truth, vol. 36 of Logic, Epistemology, and the Unity of Science, Springer.

● Badici, Emil, 2008, “The liar paradox and the inclosure schema 1”, Australasian Journal of Philosophy, 86(4): 583–596.

● Başkent, Can, 2016, “A Yabloesque paradox in epistemic game theory”, Synthese 1–24.

● Bartlett, S.J. (ed.), 1992, Reflexivity—A Source-Book in Self-Reference, Amsterdam: North-Holland Publishing Co.

● Bartlett, S.J. and Peter Suber (eds.), 1987, Self-Reference—Reflections on Reflexivity, Dordrecht: Martinus Nijhoff Publishers.

● Barwise, J. and J. Etchemendy, 1987, The Liar—An Essay on Truth and Circularity, New York: Oxford University Press.

● Barwise, J. and L. Moss, 1996, Vicious Circles—On the Mathematics of Non-Wellfounded Phenomena, Stanford: CSLI Publications.

● Beall, Jc, 2009, Spandrels of truth, OUP Oxford.

● –––, 2003, Liars and Heaps: New Essays on Paradox, Oxford: Clarendon.

● –––, 2007, Revenge of the Liar: New essays on the paradox, Oxford: Oxford University Press.

● –––, 2014a, “Finding tolerance without gluts”, Mind 123(491): 791–811.

● –––, 2014b, “End of inclosure”, Mind 123(491): 829–849.

● Bernardi, Claudio, 2001, “Fixed points and unfounded chains”, Annals of Pure and Applied Logic, 109(3): 163–178.

● Bolander, Thomas, 2002, “Self-reference and logic”, Phi News, 1: 9–44.

● Bolander, T. and V.F. Hendricks and S.A. Pedersen (eds.), 2006, Self-Reference, Stanford: CSLI Publications.

● Boolos, G., 1993, The Logic of Provability, Cambridge: Cambridge University Press.

● Brandenburger, Adam and Keisler, H. Jerome, 2006, “An impossibility theorem on beliefs in games”, Studia Logica, 84(2): 211–240.

● Butler, Jesse M., 2017, “An entirely non-self-referential Yabloesque paradox”, Synthese 1–13.

● Cantini, Andrea, 2009, “Paradoxes, self-reference and truth in the 20th century”, Handbook of the History of Logic, 5: 875–1013.

● –––, 1996, Logical Frameworks for Truth and Abstraction—An Axiomatic Study, Amsterdam: North-Holland Publishing Co.

● –––, 2009, “Paradoxes, self-reference and truth in the 20th century”, Handbook of the History of Logic, vol. V, Amsterdam: Elsevier, pp. 875–1013.

● –––, 2015, “On stratified truth”, in Unifying the philosophy of truth, Netherlands: Springer.

● Cantor, Georg, 1895, “Beiträge zur begründung der transfiniten mengenlehre”, Mathematische Annalen, 46(4): 481–512.

● –––, 1891, “Über eine Elementare Frage der Mannigfaltigkeitslehre,” Jahresbericht der Deutschen Mathematiker-Vereinigung, 1: 75–78.

● Cieśliński, C. and R. Urbaniak, 2013, “Gödelizing the Yablo Sequence”, Journal of Philosophical Logic 42(5): 679–695.

● Caret, Colin R. and Zach Weber, 2015, “A Note on Contraction-Free Logic for Validity”, Topoi 34(1): 63–74.

● Chapuis, A. and A. Gupta, 2000, Circularity, Definition and Truth, New Delhi: Indian Council of Philosophical Research.

● Cobreros, Pablo, Paul Égré, David Ripley, and Robert van Rooij, 2014, “Reaching Transparent Truth”, Mind 122(488): 841–866.

● Colyvan, Mark, 2009, “Vagueness and Truth”, in Dyke, Heather (ed.): From Truth to Reality: New Essays in Logic and Metaphysics, Oxford: Routledge.

● Cook, Roy, 2007, “Embracing revenge: on the indefinite extensibility of language”, Revenge of the Liar: New Essays on the Paradox, Oxford: Oxford University Press.

● –––, 2004, “Patterns of paradox”, The Journal of Symbolic Logic, 69(3): 767–774.

● –––, 2009, “What is a truth value and how many are there?”, Studia Logica, 92(2): 183–201.

● –––, 2013, Paradoxes, Polity Press.

● –––, 2014, The Yablo paradox: An essay on circularity, Oxford: Oxford University Press.

● Dyrkolbotn, S. and M. Walicki, 2014, “Propositional discourse logic”, Synthese, 191(5): 863–899.

● Erickson, G. W. and J. A. Fossa, 1998, Dictionary of Paradox, Lanham: University Press of America.

● Feferman, S., 1984, “Kurt Gödel: conviction and caution”, Philosophia Naturalis, 21: 546–562.

● –––, 1984a, “Toward useful type-free theories I”, The Journal of Symbolic Logic, 49: 75–111.

● –––, 1991, “Reflecting on incompleteness”, The Journal of Symbolic Logic, 56: 1–49.

● Field, Hartry, 2003, “A revenge-immune solution to the semantic paradoxes”, Journal of Philosophical Logic, 32(2): 139–177.

● –––, 2008, Saving truth from paradox, Oxford University Press, USA.

● Fitting, M., 1986, “Notes on the mathematical aspects of Kripke’s theory of truth”, Notre Dame Journal of Formal Logic, 27(1): 75–88.

● –––, 1997, “A theory of truth that prefers falsehood”, The Journal of Philosophical Logic, 26(5): 477–500.

● –––, 2006, “Bilattices are nice things.”, in Bolander, Hendricks, Pedersen (eds.), Self-reference, Stanford: CSLI Publications.

● Forster, T. E., 1995, Set Theory with a Universal Set, New York: The Clarendon Press.

● French, Rohan, 2016, “Structural reflexivity and the paradoxes of self-reference”, Ergo, an Open Access Journal of Philosophy 3.

● Gaifman, Haim, 1988, “Operational pointer semantics: Solution to self-referential puzzles i”, in Proceedings of the 2nd Conference on Theoretical Aspects of Reasoning about Knowledge, Morgan Kaufmann Publishers Inc., 43–59.

● –––, 1992, “Pointers to truth”, The Journal of Philosophy, 89(5): 223–261.

● –––, 2000, “Pointers to propositions”, in A. Chapuis and A. Gupta, Circularity, definition and truth, Indian Council of Philosophical Research, 79–121.

● Gilmore, P. C., 1974, “The consistency of partial set theory without extensionality”, Axiomatic set theory (Proc. Sympos. Pure Math., Vol. XIII, Part II), pp. 147–153, Providence RI: Amer. Math. Soc.

● Gödel, K., 1931, “Über formal unentscheidbare Satze der Principia Mathematica und verwandter Systeme I”, Monatshefte für Mathematik und Physik, 38: 173–198.

● Gupta, A. and N. Belnap, 1993, The Revision Theory of Truth, Cambridge MA: MIT Press.

● Gupta, A. and S. Standefer, 2017, “Conditionals in theories of truth”, Journal of Philosophical Logic 46(1): 27–63.

● Halbach, Volker, 2008, “On a side effect of solving Fitch’s paradox by typing knowledge”, Analysis, 68(298): 114–120.

● –––, 2011, Axiomatic theories of truth, Cambridge: Cambridge University Press.

● Halbach, Volker, and Albert Visser, 2014a, “Self-reference in Arithmetic I”, The Review of Symbolic Logic 7(4): 671–691.

● –––, 2014b, “Self-reference in arithmetic II”, The Review of Symbolic Logic 7(4): 692–712.

● Halbach, Volker, and Shuoying Zhang, 2017, “Yablo Without Gödel”, Analysis 77(1): 53–59.

● Hsiung, Ming, 2017, “Boolean Paradoxes and Revision Periods”, Studia Logica 1–34.

● van Heijenort, J., 1967, From Frege to Gödel. A source book in mathematical logic, 1879–1931, Cambridge (MA): Harvard University Press.

● Horsten, Leon, 2011, The Tarskian Turn: Deflationism and Axiomatic Truth, Cambridge, MA: MIT Press.

● Kripke, S., 1975, “Outline of a Theory of Truth”, The Journal of Philosophy, 72: 690–716.

● Leach-Krouse, Graham, 2014, “Yablifying the Rosser sentence”, Journal of Philosophical Logic 43(5): 827–834.

● Leitgeb, Hannes, 2008, “On the probabilistic convention t”, The Review of Symbolic Logic, 1(02): 218–224.

● Mares, Edwin and Francesco Paoli, 2014, “Logical Consequence and the Paradoxes”, Journal of Philosophical Logic, 43(2–3): 439–469.

● Martin, R. L., 1984, Recent Essays on Truth and the Liar Paradox, Oxford: Oxford University Press.

● Martin, R. L. and P. W. Woodruff, 1975, “On representing ‘True-in-L’ in L”, Philosophia, 5: 213–217.

● McGee, V., 1990, Truth, Vagueness, and Paradox—An Essay on the Logic of Truth, Indianapolis: Hackett Publishing Co.

● –––, 1992, “Maximal consistent sets of instances of Tarski’s Schema (T)”, The Journal of Philosophical Logic, 21(3): 235–241.

● Montague, R., 1963, “Syntactical treatment of modality, with corollaries on reflection principles and finite axiomatizability”, Acta Philosophica Fennica, 16: 153–167.

● Murzi, Julien, and Massimiliano Carrara, 2015, “Paradox and logical revision. A short introduction”, Topoi 34(1): 7–14.

● Odintsov, Sergei P. and Heinrich Wansing, 2015, “The logic of generalized truth values and the logic of bilattices.” Studia Logica, 103(1): 91–112.

● Pacuit, Eric, 2007, “Understanding the Brandenburger-Keisler paradox”, Studia Logica, 86(3): 435–454.

● Picollo, Lavinia María, 2013, “Yablo’s paradox in second-order languages: Consistency and unsatisfiability”, Studia Logica 101(3): 601–617.

● Pelling, Charlie, 2011, “A self-referential paradox for the truth account of assertion”, Analysis, 71(4): 688–688.

● Perlis, D. and V. S. Subrahmanian, 1994, “Meta-languages, Reflection Principles and Self-Reference”, Handbook of Logic in Artificial Intelligence and Logic Programming, 2: 323–358.

● Priest, Graham, 2010a, “Badici on inclosures and the liar paradox”, Australasian Journal of Philosophy, 88(2): 359–366.

● –––, 2010b, “Inclosures, vagueness, and self-reference”, Notre Dame Journal of Formal Logic, 51(1): 69–84.

● –––, 2013, “Vague Inclosures”, in Paraconsistency: Logic and Applications, Netherlands: Springer.

● –––, 1987, In Contradiction—A Study of the Transconsistent, Dordrecht: Martinus Nijhoff Publishers.

● –––, 1994, “The Structure of the Paradoxes of Self-Reference”, Mind, 103: 25–34.

● –––, 1995, Beyond the Limits of Thought, Cambridge: Cambridge University Press.

● –––, 1997, “Yablo’s paradox”, Analysis 57(4): 236–242.

● Quine, W.V., 1937, “New foundations for mathematical logic”, American Mathematical Monthly, 44: 70–80.

● Rabern, Landon, and Brian Rabern and Matthew Macauley, 2013, “Dangerous reference graphs and semantic paradoxes”, Journal of Philosophical Logic 42(5): 727–765.

● Rosado Haddock, G. E., 2001, “Recent truth theories: A case study”, Axiomathes, 12(1): 87–115.

● Russell, B., 1905, “On some difficulties in the theory of transfinite numbers and order types”, Proceedings of the London Mathematical Society, 4: 29–53.

● Schindler, Thomas, 2017, “Some Notes on Truths and Comprehension”, Journal of Philosophical Logic 1–31.

● Schlenker, Philippe, 2010, “Super liars”, The Review of Symbolic Logic, 1(1): 1–41.

● Shapiro, Lionel, 2015, “Naive Structure, Contraction and Paradox”, Topoi, 34(1): 75–87.

● Sheard, M., 1994, “A guide to truth predicates in the modern era”, The Journal of Symbolic Logic, 59(3): 1032–1054.

● Simmons, K., 1993, Universality and the Liar—An Essay on Truth and the Diagonal Argument, Cambridge: Cambridge University Press.

● Slater, Hartley, 2002, “The Fallacy in Russell’s Schema”, Russell: the Journal of Bertrand Russell Studies, 22(2): 4.

● –––, 2010, “What Priest (amongst many others) has been missing”, Ratio, 23(2): 184–198.

● Smullyan, R. M., 1992, Gödel’s Incompleteness Theorems, Oxford: Oxford University Press.

● –––, 1994, Diagonalization and self-reference, Oxford: Oxford University Press.

● –––, 2006, “Self-Reference in All Its Glory!”, in Bolander, Hendricks, Pedersen (eds.), Self-reference, Stanford: CSLI Publications.

● Snapper, Jeff, 2012, “The liar paradox in new clothes”, Analysis, 72(2): 319–322.

● Tarski, A., 1935, “Der Wahrheitsbegriff in den formalisierten Sprachen”, Studia Philosophica, 1: 261–405.

● –––, 1968, Undecidable Theories, Amsterdam: North-Holland Publishing Co.

● Thomason, R., 1980, “A note of syntactical treatments of modality”, Synthese, 44: 391–395.

● Tourville, Nicholas, and Roy T. Cook, “Embracing the Technicalities: Expressive Completeness and Revenge”, The Review of Symbolic Logic, 9(2): 325–358.

● Turing, A.M., 1936, “On Computable Numbers, With an Application to the Entscheidungsproblem”, Proceedings of the London Mathematical Society, 42(2): 230–265; correction ibid., 43: 544–546 (1937).

● Tucker, Dustin and Richmond H. Thomason, 2011, “Paradoxes of intensionality”, The Review of Symbolic Logic, 4(03): 394–411.

● Urbaniak, Rafał, 2009, “Leitgeb, ‘about,’ Yablo”, Logique & Analyse, 207: 239–254.

● Visser, A., 1989, “Semantics and the liar paradox”, Handbook of Philosophical Logic (Vol. IV), Dordrecht: Kluwer, pp. 617–706.

● Walicki, Michał, 2009, “Reference, paradoxes and truth”, Synthese, 171(1): 195–226.

● Weber, Zach, 2010a, “Explanation and solution in the inclosure argument”, Australasian Journal of Philosophy, 88(2): 353–357.

● –––, 2010b, “A Paraconsistent Model of Vagueness”, Mind 119: 1026–1045.

● Weber, Zach, et al., 2014, “Tolerating gluts”, Mind 123(491): 813–828.

● Wintein, Stefan, 2012, “Assertoric semantics and the computational power of self-referential truth”, Journal of philosophical logic, 41(2): 317–345.

● Yablo, Stephen, 1985, Yablo, “Truth and reflection”, Journal of Philosophical Logic, 14(3): 297–349.

● –––, 1993, “Paradox without self-reference”, Analysis, 53: 251–252.

● –––, 2006, “Circularity and Paradox”, in Bolander, Hendricks, Pedersen (eds.), Self-reference, Stanford: CSLI Publications.

● Zardini, Elia, 2011, “Truth without contra(di)ction”, Review of Symbolic Logic, 4(4): 498–535.

● Zhong, Haixia, 2012, “Definability and the structure of logical paradoxes”, Australasian Journal of Philosophy, 90(4): 779–788.

● Zwicker, W.S., 1987, “Playing Games with Games: The Hypergame Paradox,” The American Mathematical Monthly, 94(6): 507–514.