Машины Тьюринга
Впервые опубликовано 14 сентября 1995 года; содержательно переработано 26 июня 2012 года.
Машины Тьюринга, впервые описанные Аланом Тьюрингом (Turing 1937а), представляют собой теоретические вычислительные устройства, предназначенные для того, чтобы помочь оценить объем и ограничения того, что поддается вычислению.
Тьюринга интересовал один из фундаментальных вопросов в философии информатики: как определить, вычислима ли задача. Интуитивно предполагается, что если возможно представить задачу в виде последовательности команд (операторов), которая приведет в итоге к выполнению ее машиной, то задача вычислима. Такой набор команд называется эффективной процедурой или алгоритмом задачи. Проблема в подобного рода предположении заключается в том, что так называемая эффективная процедура может зависеть от возможностей машины, которой мы передаем команды на выполнение. В принципе устройства с разными возможностями могут выполнять различные наборы команд, а следовательно, мы можем иметь дело с различными классами вычислимых задач (см. статью о вычислимости и сложности).
Тьюринг представил класс устройств, которые стали называться машинами Тьюринга. Благодаря этим устройствам появилось формальное представление вычислимости, которое мы будем называть вычислимостью по Тьюрингу. Задача вычислима по Тьюрингу, если она может быть решена какой-либо машиной Тюринга.
Утверждение о том, что представление Тьюринга точно охватывает интуитивную идею эффективной процедуры, называется тезисом Черча — Тьюринга. Данное положение недоказуемо, поскольку оно касается некоторого соотношения между формальным понятием и интуицией. Тезис мог бы быть опровергнут с помощью интуитивно-приемлемого алгоритма задачи, невычислимой по Тьюрингу, однако подобного рода контрпример так и не был обнаружен. Другие независимые определения вычислимости, которые опираются на альтернативные предпосылки, такие как рекурсивные функции и машины абак, оказались эквивалентными вычислимости по Тьюрингу. Эти факты указывают на то, что данное представление вычислимости обладает по меньшей мере некоторым реальным содержанием.
Машины Тьюринга — это не физические, а математические объекты. Для их построения не требуются ни паяльники, ни кремниевые микросхемы. Архитектура такой машины описывается просто, а действия, которые она выполняет, просты и недвусмысленны. Тьюринг признавал, что необязательно говорить о том, как машина выполняет свои действия; достаточно принять, что машина может выполнять определенные действия и что эти действия могут быть однозначно описаны.
Определение машин Тьюринга
Машина Тьюринга — это машина состояний. В любой момент времени машина находится в одном из конечного числа состояний. Команды для машины Тьюринга заключаются в заданных условиях, при которых машина перейдет из одного состояния в другое.
В литературе имеется несколько различных определений машины Тьюринга. Они различны в конкретике, но сходятся в том, что одни и те же задачи оказываются вычислимыми по Тьюрингу в любой формулировке. Определение, приводимое в настоящей статье, — лишь одно из распространенных; некоторые другие версии обсуждаются в разделе 3.
Машина Тьюринга имеет бесконечную одномерную ленту, разделенную на ячейки. По сложившейся традиции лента представляется горизонтальной, а ячейки в ней располагаются слева направо. Единственный конец ленты располагается в левой ее части, и лента неограниченно простирается вправо. Каждая ячейка может содержать один символ — «0» или «1».
У машины есть головка чтения/записи, которая сканирует отдельную ячейку на ленте. Головка чтения/записи может двигаться влево или вправо по ленте, последовательно сканируя ячейки.
Действие машины Тьюринга полностью определяется: (1) ее текущим состоянием; (2) символом в ячейке, которую в данный момент сканирует головка, и (3) таблицей правил перехода, которая служит в качестве «программы» машины.
Каждое правило перехода представляет собой кортеж из четырех элементов (4-кортеж):
⟨ Состояние-текущее, Символ, Состояние-следующее, Действие ⟩
Это аналогично следующей фразе: «если машина находится в Состоянии-текущее и сканируемая ячейка содержит Символ, то следует перейти в Состояние-следующее, выполнив Действие». В качестве выполняемого действия машина Тьюринга может поставить символ в текущей ячейке на ленте (который мы обозначаем как «Символ») или переместить головку на одну ячейку влево или вправо, что мы обозначаем символами «<<» и «>>» соответственно.
Если машина достигает такого состояния, в котором нет однозначного правила для выполнения — его нет или правил несколько, — то машина останавливается.
В современной терминологии лента — это запоминающее устройство машины, в то время как головка чтения/записи представляет собой шину памяти, через которую машина осуществляет доступ к данным (и их обновление). Следует отметить два важных момента, связанных с данной конфигурацией. Первый относится к определению машины в целом: лента машины имеет бесконечную длину. Данное утверждение соответствует допущению, что память машины бесконечна. Второй момент относится к определению вычислимости по Тьюрингу: функция будет вычислимой по Тьюрингу, если существует набор команд, выполнение которых приведет машину Тьюринга к ее вычислению, независимо от того, сколько времени будет затрачено. Можно сказать, здесь мы имеем дело с допущением, что машина располагает бесконечным временем, необходимым для завершения вычислений.
Эти два допущения используются для удостоверения, что итоговое определение вычислимости не окажется слишком узким. Таким образом, никакая вычислимая функция не утратит вычислимости по Тьюрингу просто из-за недостатка времени или памяти. Отсюда следует, что могут существовать некоторые функции, вычислимые по Тьюрингу, выполнение которых невозможно для существующих компьютеров, вероятно, поскольку ни один из них не имеет достаточно памяти для выполнения задачи. Некоторые функции, вычислимые по Тьюрингу, нельзя вычислить на практике, потому что для этого может потребоваться больше памяти, чем можно построить, используя все атомы во Вселенной (а их число конечно). И наоборот, результат, который показывает, что функция не является вычислимой по Тьюрингу, имеет очень большую силу, поскольку из него однозначно следует, что для такого вычисления в принципе не может быть создан никакой компьютер. В разделе 5 показано, что некоторые функции не являются вычислимыми по Тьюрингу.
Формализованное определение
Такие понятия, как «лента» и «головка чтения/записи», помогают интуитивному пониманию машин, а также немного рассказывают о том времени, в которое работал Тьюринг. Однако они не имеют особого значения для определения. В ситуациях, когда требуется формальный анализ машин Тьюринга, более уместным представляется определение в математических терминах. Чисто формально можно определить, что в состав машины входят:
конечное множество состояний Q, в котором можно выделить начальное состояние;
конечное множество символов Σ.
Вычислительное состояние описывает все, что нужно знать о машине в данный момент времени при выполнении задачи. На любом шаге выполнения s:
Qs, принадлежащее Q, — состояние, в котором находится машина Тьюринга;
σs, функция от целых чисел, входящих в Σ, описывает содержание каждой ячейки ленты;
натуральное число hs — индекс ячейки, сканируемой в настоящий момент.
Функция перехода машины δ — это функция, приводящая от одних вычислительных состояний («аргумент») к другим вычислительным состояниям («функция»); при этом если δ(S) = T, то
σT согласуется с σS везде, исключая hS (но необязательно исключая).
Если σS(hS) ≠ σT(hS), то hT = hS; в противном случае |hT − hS| ≤ 1
Функция перехода определяет новое содержание ленты, выдавая новую функцию σ, но эта новая функция ограничивается тем, что ее значение должно быть очень близко к старому. В первом вышеупомянутом ограничении выдвигается утверждение, что содержание ячейок ленты везде одинаково, кроме (возможно) ячейки, которая сканируется в настоящий момент. Поскольку машины Тьюринга могут или менять содержимое ячейки, или перемещать головку, при условии изменения ячейки головка не должна перемещаться в сторону перехода, а при условии отсутствия изменения содержимого головка перемещается максимум на одну ячейку в любом направлении. В этом состоит смысл второго вышеупомянутого ограничения.
Данное определение близко к приведенному в статье о вычислимости и сложности. Значительное различие состоит в том, что, согласно альтернативному определению, машина может написать новый символ, равно как и перемещать головку при любом переходе. Такое различие не меняет набор функций, вычислимых по Тьюрингу, и упрощает формальное определение путем исключения второго условия, налагаемого на функцию перехода в нашем определении. Согласно обоим формальным определениям, в качестве алфавита символов на ленте может выступать любое конечное множество, в то время как первоначальное определение настаивает на том, что Σ={0,1}. Данное различие, однако, также не затрагивает определение множества функций, вычислимых по Тьюрингу.
Описание машин Тьюринга
Все машины Тьюринга имеют одинаковый механизм. Одна машина Тьюринга выполняет одну задачу, а вторая — другую, поскольку таковы их таблицы правил перехода, которые устанавливают программу машины, и таковы их заданные начальные состояния. В дальнейшем мы будем предполагать, что выполнение операций машина начинает с состояния, наименьшего по порядковому номеру.
Таким образом, можно описать машину Тьюринга, задав только 4-кортежи, которые составляют ее программу. Далее приведены строки, описывающие простую машину.
⟨ s0, 1, s0, >> ⟩
⟨ s0, 0, s1, 1 ⟩
⟨ s1, 1, s1, << ⟩
⟨ s1, 0, s2, >> ⟩
Эта машина имеет три состояния, обозначенные s0, s1 и s2. Первые две команды описывают то, что происходит в состоянии s0. Существуют две возможности. Машина сканирует «1» — в данном случае головка перемещается вправо и остается в состоянии s0. Или машина переходит из состояния s0 в s1 при условии сканирования «0». В таком случае она записывает «1». Следующие две команды описывают то, что происходит в состоянии s1. При сканировании значения «1» машина перемещает головку влево, оставаясь в состоянии s1. Если машина сканирует «0», то головка перемещается вправо и машина переходит в состояние s2. Поскольку для состояния s2 нет команд, машина останавливается, как только она достигает состояния s2.
Когда мы занимаемся изучением поведения машины Тьюринга, проще и, вероятно, точнее будет представить ее при помощи диаграммы состояний. На рис. 1 машина показана в таком виде.
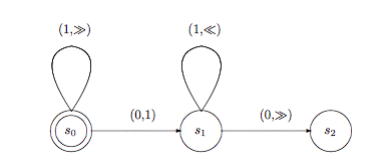
Состояния на диаграмме представлены в виде кругов; при этом двойной круг соответствует начальному состоянию. Переход представлен стрелкой, идущей от одного круга к другому (возможно, к тому же самому). Над стрелками обозначены пары, где слева в скобках находится символ, который должен быть отсканирован для того, чтобы перейти по стрелке, а справа — действие, которое следует выполнить при переходе. Действие окажется либо символом, который требуется записать, либо операцией «<<» или «>>», подразумевающей перемещение налево или направо.
Далее мы опишем машины Тьюринга в виде машинных состояний.
Примеры
Чтобы говорить о машине Тьюринга, выполняющей полезную нагрузку, нужно выполнить интерпретацию символов, записанных на ленте. Например, если мы хотим спроектировать машину, выполняющую математическую функцию, например, сложение, то следует описать, каким образом интерпретируются единицы и нули, появляющиеся как числа на ленте.
В следующем примере мы представим число n как блок из n+1 копий символа «1» на ленте. Таким образом, мы представим число 0 как один символ «1», а число 3 — как последовательность из четырех «1».
Необходимо также сделать несколько допущений о конфигурации ленты в момент начала и в момент завершения работы машины для того, чтобы интерпретировать вычисление. Предположим, что если вычисляемая функция требует n аргументов, то машина Тьюринга начнет со сканирования головкой крайней левой ячейки с символом «1», входящей в последовательность из n блоков, содержащих копии «1». Блоки с «1», представляющие аргументы, должны быть разделены единичным вхождением символа «0». Например, для вычисления сложения «3+4» машина Тьюринга построит нижеследующую конфигурацию, где многоточия показывают, что лента содержит только нули в тех ячейках, которые мы не видим, а стрелка, направленная вверх, указывает на ячейку, сканируемую в настоящий момент.

Здесь машина, выполняющая операцию сложения, берет два аргумента, соответствующие числам, которые следует сложить, начиная с крайней левой единицы первого аргумента. Аргументы разделены одним нулем (как требуется); первый блок содержит четыре символа «1» (что соответствует числу 3), а второй блок — пять символов «1» (это соответствует числу 4).
По завершении операции конфигурация машины также должна быть стандартной. На ленте должен быть отдельный блок символов «1», и машина должна сканировать крайний слева символ «1». Если машина корректно вычисляет функцию, то этот блок должен содержать правильный ответ. Таким образом, выполняющая сложение машина, начавшая вычисление в вышеприведенной конфигурации, должна закончить операцию, когда лента примет вид, показанный ниже.

Принятие данного условия для терминальной конфигурации машины Тьюринга означает, что мы можем строить машины, отождествляя конечное состояние машины с начальным состоянием следующей конфигурации.
При таких условиях диаграмма состояний на рис. 1 описывает машину, которая вычисляет функцию следования (инкремент). Начав в стандартной конфигурации на ленте с числом n, машина остановится в стандартной конфигурации с числом n+1. Машина выполняет это, используя состояние s0, чтобы просканировать ленту далее направо до первого символа «0» после отдельного блока символов «1». Далее машина заменяет этот символ «0» на «1» и сканирует налево в состоянии s1, пока не будет найден символ «0» (это первый ноль от блока символов «1» при сканировании влево). Затем сканирование происходит в обратном направлении до первого символа «1», и машина останавливается в состоянии s2.
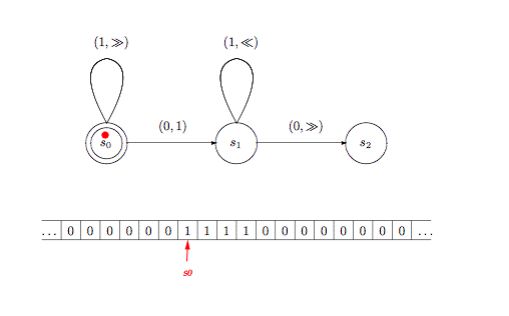
На схеме выше показано начальное состояние. Щелкните по картинке, чтобы запустить анимацию, показывающую, как машина выполняет задание. Щелкните еще раз, чтобы остановить и перезапустить анимацию.
На другом примере рассмотрим машину (рис. 2), вычисляющую функцию сложения. Начав на ленте, представляющей числа n и m, машина останавливается, когда лента соответствует уже сумме n+m.
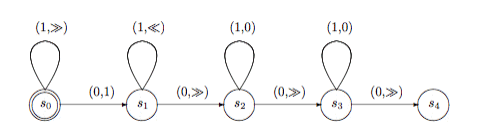
Заметьте, что такая машина похожа на машину с инкрементом (то есть прибавляющую единицу) в том плане, что состояния от s0 до s2 заставляют машину записать символ «1» справа от первого блока символов «1» и вернуть головку к крайнему слева символу «1». В стандартной конфигурации, используемой для сложения, данная операция соединяет два блока символов «1» в один, содержащий (n+1)+1+(m+1) копий символов «1». Таким образом, при переходе в состояние s2 на ленте будет число n+m+2. Чтобы это исправить, нам нужно удалить две копии символа «1», что достигается через состояния s2 и s3, в каждом из которых происходит замена «1» на «0», после чего головка перемещается вправо.
Поскольку лента изначально содержит как минимум два символа «1» и мы добавляем еще один, удаление двух копий «1» приведет к тому, что в конце вычисления на ленте останется как минимум одна единица, и при этом мы будем сканировать крайнюю левую единицу.
Мгновенные описания вычисления
Вспомним, что ранее мы определили, что рабочее состояние машины Тьюринга может быть описано такими параметрами, как название текущего состояния машины Qs, символы на ленте σs и сканируемая в настоящий момент ячейка hs. Такое описание показано на рис. 3, где стрелка указывает на сканируемую в данный момент ячейку, а название текущего состояния указано под стрелкой.
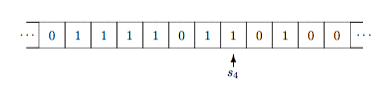
Рис. 3. Мгновенное описание вычисления, производимого машиной Тьюринга
Данная схема показывает, что машина Тьюринга находится в состоянии s4, сканируя указанную ячейку на ленте. Предполагается, что лента содержит символы «0» во всех ячейках, которые не видны.
Разновидности машин Тьюринга
Здесь мы изложили одну из наиболее распространенных формулировок основной идеи Тьюринга. Существуют разнообразные формулировки, которые оказываются эквивалентными ей, и различные авторы представляют машины Тьюринга, используя одну из них. Поскольку все они, вероятно, эквивалентны друг другу, мы можем рассматривать любую удобную нам формулировку в качестве определения машины Тьюринга.
Формулировка F1 и формулировка F2 эквивалентны, если для каждой машины, описанной в формулировке F1, существует машина, описанная в F2, у которой ввод и вывод осуществляются таким же образом, как в F1, и наоборот. Так. когда мы начинаем выполнять операции на той же самой ленте в той же самой ячейке, мы завершим выполнять операции на той же ячейке и на той же ленте.
Бесконечные ленты, имеющие два направления
В нашей исходной формулировке мы постулировали, что лента имеет конец слева и бесконечно простирается слева направо. Если отменить данное ограничение и позволить ленте бесконечно простираться влево и вправо, то мы придем к новой формулировке машин Тьюринга. Можно было бы ожидать, что лента, бесконечная в двух направлениях, позволит увеличить число вычислимых функций, однако этого не происходит. Если для вычисления функции существует машина с лентой, неограниченной слева или справа, то найдется машина с лентой, ограниченной в одном из направлений, которая сможет рассчитать такую же функцию.
Произвольное число головок чтения/записи
Изменив определение машины Тьюринга путем введения утверждения о наличии нескольких головок чтения/записи, мы не вносим никаких исправлений в понятие вычислимости по Тьюрингу.
Машины с несколькими лентами
Вместо одной бесконечной ленты можно рассмотреть машины, обладающие несколькими такими лентами. Формулировка такой машины предполагает, что команды должны определить, какую ленту следует сканировать в данный момент, где нужно написать новый символ и какую головку следует перемещать. Опять же, данное определение эквивалентно первоначальному.
Двумерные ленты
Вместо одномерной бесконечной ленты мы можем рассмотреть двумерную «ленту», которая бесконечно простирается вверх, вниз, влево и вправо. К определению следует добавить, что головка чтения/записи может перемещаться вверх и вниз в дополнение к движению влево и вправо. Опять же, данное определение эквивалентно первоначальному.
Произвольное перемещение головки
Если к определению машины Тьюринга мы добавим условие, что головка может перемещаться на произвольное число ячейок при любом данном переходе, то понятие вычислимости по Тьюрингу останется неизменным.
Произвольный конечный алфавит
В оригинальном определении нам можно использовать только два символа на ленте. В действительности же мощность машины Тьюринга не увеличится, если мы будем использовать любой алфавит, содержащий конечное число символов.
Формулировка из пяти строк
Общий принцип описания машины Тьюринга состоит в том, что машина может как записывать символы, так и перемещать головку одновременно за один переход. Данная формулировка требует замены 4-кортежей первоначального определения 5-кортежами вида
⟨ Состояние0, Символ, Состояние-новое, Символ-новый, Перемещение ⟩,
где Символ-новый — это записанный символ, а Перемещение — одна из операций «<<» или «>>».
Как и прежде, эта добавочная степень свободы не приводит к новому определению вычислимости по Тьюрингу. Для каждой новой машины найдется старая с теми же свойствами.
Недетерминированные машины Тьюринга
На вид более существенное изменение в формулировке машины Тьюринга допускает, что машина может проводить параллельно несколько различных вычислений. В исходной формулировке мы постулировали, что если бы машина определила несколько переходов для пары данных состояний/символов и машина находилась бы в одном из таких состояний, то она бы остановилась. В данной новой формулировке выполняются все переходы и все вычисления ведутся параллельно. Можно представить, что машина порождает точную копию самой себя, включая ленту для каждого доступного перехода, и каждая машина продолжает вычисление. Если какая-либо из машин успешно завершает работу, то завершается общее вычисление с принятием ленты той машины. Обратите внимание на слово «успешно» в предыдущем предложении. В этой формулировке некоторые состояния обозначены как «принимающие состояния». Когда машина завершает операцию в одном из таких состояний, вычисление является успешным; в противном случае вычисление считается неуспешным, и любая другая машина продолжает поиск успешного решения.
Введение недетерминированности в определение машин Тьюринга не изменяет определения вычислимости по Тьюрингу.
В своем первоначальном определении машин Алан Тьюринг использовал представление через 5-кортежи. Эмиль Пост ввел представление машины Тьюринга через 4-кортежи, а также двустороннюю бесконечную ленту.
Более сложная машина
В дополнение к выполнению числовых функций с использованием унарного представления чисел можно выполнять и другие задачи, такие как копирование блоков символов, удаление блоков и т.д. Здесь мы приводим пример машины Тьюринга, которая, начав в стандартной конфигурации, содержащей отдельный блок символов «1», останавливается, когда лента содержит две копии этого блока. При этом два блока разделены одним нулем. Машина использует алфавит, состоящий из символов «0», «1» и «А».
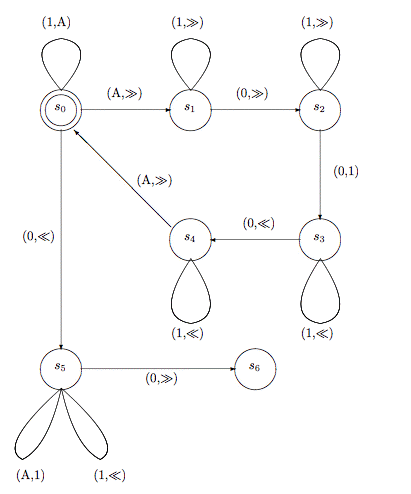
Рис. 4. Машина для копирования блока символов «1»
Действие этой машины заключается в многократной замене исходных символов «1» на «А» и последующей записи нового символа «1» справа от всех оставшихся на ленте «1» после того, как был поставлен ноль между исходным блоком и копией. Когда у нас заканчиваются исходные символы «1», мы обратно превращаем символы «А» в «1».
Начальное состояние s0 используется для того, чтобы заменить символы «1» на «А» и переместиться вправо в состояние s1. В состоянии s1 мы пропускаем оставшуюся часть блока символов «1» до тех пор, пока не найдем «0» (разделитель блоков). В s2 мы пропускаем все «1», двигаясь вправо от найденного символа «0» (это создаваемая нами копия блока символов «1»). Когда мы достигаем конца блока, мы находим «0», который заменяем на «1», после чего головка перемещается влево, а затем машина переходит в состояние s3. В состояниях s3 и s4 пропускаются символы «1» в направлении влево и отделяющие их «0» до тех пор, пока не будет обнаружен символ «А». Когда это происходит, мы возвращаемся назад в состояние s0 и движемся вправо.
На этом этапе либо сканируется следующий символ «1» исходного блока, либо все его символы уже заменены на «А», и мы сканируем разделитель «0». В первом случае мы заново проходим состояния s1–s4, однако во втором случае мы движемся влево в состояние s5. В этом состоянии мы повторно находим символы «А», которые заменяем на «1», и затем движемся влево. Если мы находим «0», то все символы «А» уже заменены на «1». Мы будем сканировать «0» слева от исходной ячейки, после чего мы перейдем вправо, а затем — в конечное состояние s6.
Такая копирующая машина может использоваться в сочетании с машиной сложения (см. рис. 2) для создания машины удвоения, то есть машины, которая, начав на ленте, представляющей число n, останавливается на ленте с записью 2n. Это достигается путем использования сначала копирующей машины, которая запишет на ленте две копии числа n, а затем — машины сложения, которая вычислит n+n (=2n). Нам потребуется приравнять конечное состояние копирующей машины (s6) к начальному состоянию машины сложения (s0).
Предложенная конструкция основывается на том, что копирующая машина завершает работу в стандартной позиции, которая требуется машине сложения для корректного вычисления результата. Для построения подобных машин разрабатываются машины Тьюринга, которые начинают и завершают работу в стандартной конфигурации. В данном примере копирующая машина имеет уникальное терминальное состояние, что, однако, не является необходимым. Мы можем построить машину Тьюринга, которая показывает результат своего вычисления, завершая работу в одном из ряда состояний. Мы можем соединить такую машину еще с несколькими, и при этом идентичность каждой машины будет зависеть от переключающей машины. Тем самым мы смогли бы создать машину, которая при необходимости будет прибавлять единицу к вводимому числу, если оно является четным, и удваивать его, если оно нечетное.
Что поддается вычислению
Машины Тьюринга весьма мощны. Машину Тьюринга можно создать для широкого спектра вычислительных задач. Например, как было показано, можно разработать машину Тьюринга для выполнения арифметических действий с натуральными числами.
Вычислимые числа
В исходной статье Тьюринга рассматриваются вычислимые числа. Число вычислимо по Тьюрингу, если существует такая машина Тьюринга, которая находит произвольно точное приближение к этому числу, начиная с чистой ленты. Все алгебраические числа (корни многочленов с алгебраическими коэффициентами) и многие трансцендентные математические константы, такие как e и π, вычислимы по Тьюрингу.
Вычислимые функции
Как мы уже видели, машины Тьюринга могут делать нечто большее, чем просто записывать числа. Помимо всего прочего, они могут выполнять сложение (см. рис. 2), умножение, собственное вычитание, возведение в степень, вычисление факториалов и т.п.
Характеристическая функция предиката — функция, принимающая значения TRUE (истина) или FALSE (ложь) при наличии подходящих аргументов. В качестве примера можно рассмотреть предикат ‘IsPrime’ («является простым числом»), характеристическая функция которого устанавливается в значение TRUE, если аргумент — простое число (2, 3, 5 и т.п.) и FALSE, когда аргумент принимает значения 4, 9 или 12. Обозначим TRUE как последовательность двух символов «1», а FALSE — как один символ «1». Теперь мы можем построить машину Тьюринга для вычисления характеристических функций вычислимых предикатов. Например, мы можем создать машину, которая, начав на ленте с некоторым числом, заканчивает со значением TRUE только в том случае, если число простое. Можно комбинировать результаты таких вычислений, используя булевы функции: И, НЕТ, ИЛИ, ЕСЛИ-ТОГДА-ИНАЧЕ, — каждая из которых является вычислимой по Тьюрингу.
Собственно, функции, вычислимые по Тьюрингу, — это рекурсивные функции, описание которых приводится далее.
Универсальные машины Тьюринга
Возможности машин Тьюринга нашли наиболее интересное отражение в универсальных машинах Тьюринга (УМТ). Когда машина начинает работать на ленте, содержащей кодировку другой машины Тьюринга (обозначим ее T), а затем идет ввод в T, УМТ выдает тот же результат, что и T, начавшая работу с этим вводом. По сути, УМТ может моделировать поведение любой машины Тьюринга (включая саму себя).
УМТ можно представить как программируемый компьютер. Когда УМТ получает программу (описание другой машины), в ходе обработки введенных данных она ведет себя так, как если бы была этой машиной.
Вновь заметьте, как мы ассоциируем эквивалентность ввода-вывода с «идентичным поведением». Машина T, обрабатывающая данные ввода t, выполняет, вероятно, гораздо меньше переходов, чем УМТ, которая моделирует T, обрабатывающую t, но в целях упрощения нашего изложения этот факт не учитывается.
Чтобы спроектировать такую машину, сначала необходимо определить, каким именно образом символы на ленте будут представлены для УМТ. Для этого вспомним, что машины Тьюринга формально представляют из себя набор из 4-кортежей. Первым делом мы разработаем кодировку для одного набора команд, а затем — для последовательности наборов.
Кодирование машин Тьюринга
Каждый 4-кортеж в спецификации машины будет закодирован как последовательность четырех блоков символов «1», разделенных одним символом «0».
Первый блок единиц закодирует число текущего состояния в соответствии с изложенным выше унарным представлением (n+1 единиц представляют число n).
Следующий блок единиц закодирует текущий символ, используя один символ «1» для обозначения символа «0» и две единицы для обозначения символа «1» (опять же, поскольку мы не можем использовать нули для представления «0»).
Третий элемент кортежа будет представлять собой новое число состояния в унарной записи чисел.
Четвертый элемент представляет действие, при этом имеются четыре возможности: символы будут закодированы, как показано выше, при этом блок из трех символов «1» означает движение влево («<<»), а блок из четырех «1» означает движение вправо («>>»).
Используя эти конвенции, на рис. 5 мы представим кортеж ⟨0, «1», 0, >>⟩.

Рис. 5. Кодировка набора команд ⟨0, «1», 0, >>⟩
Чтобы закодировать машину целиком, нужно просто написать наборы команд на ленте в любом порядке, отделяя один набор от другого двумя пустыми ячейками таким образом, чтобы можно было видеть, где заканчивается каждый кортеж. Представление ленты машины, прибавляющей единицу (см. рис. 1), окажется немного устрашающей вереницей (см. рис. 6).
… 010110101111 00 101011011 00 110110110111 00 11010111011110 …
Рис. 6. Кодировка машины, показанной на рис. 1
Такая конструкция показывает возможность кодировки кортежей машины Тьюринга на ее ленте. (Мы сделали это, используя лишь алфавит из нулей и единиц {0, 1}, в то время как из предыдущего результата нам известно, что можно использовать расширенный алфавит, приводящий к более ясному представлению данных.) Мы хотим, чтобы УМТ начала работу на ленте, содержащей описание машины Тьюринга в этой кодировке, за которым следуют аргументы для описываемой машины. Мы принимаем, что описание машины Тьюринга будет отделено от аргументов блоком из трех символов «0» таким образом, что УМТ сможет распознать, где заканчиваются кортежи и начинаются аргументы. Для машины, прибавляющей единицу, требуется один аргумент, который поможет нам запустить УМТ на ленте, показанной выше, за которой следует четыре символа «0» и, предположим, пять «1». УМТ должна завершить работу на ленте, содержащей отдельный блок из шести символов «1», точно вычислив то, что смогла бы найти машина, прибавляющая единицу, если бы ее запустили на блоке из пяти символов «1».
Что не поддается вычислению
В предыдущем разделе был описан способ кодирования машин Тьюринга для передачи вводных данных в универсальную машину Тьюринга. Кодировка машины Тьюринга представляет собой последовательность символов «0» и «1», и любая такая последовательность может быть проинтерпретирована как натуральное число. Можно представить кодировку машины Тьюринга в виде натурального числа, выступающего серийным номером этой машины. Благодаря способу работы кодировки, каждая машина Тьюринга будет иметь определенный серийный номер. Поскольку все серийные номера — это натуральные числа, номер отдельной машины Тьюринга является счетно бесконечным.
С другой стороны, количество функций натуральных чисел рассчитать невозможно. Функций натуральных чисел (несчетно) больше, чем машин Тьюринга. Отсюда следует, что существуют невычислимые функции, то есть функции, результаты которых не могут быть найдены машиной Тьюринга, поскольку для вычисления таких функций просто не существует достаточно машин Тьюринга.
Доказательство от счетности несколько неудовлетворительно, так как оно говорит о существовании невычислимых функций, но не дает ни одного релевантного примера. Здесь мы приводим два примера невычислимых функций.
«Поиск усердных бобров»
Представим, что машина Тьюринга, которая начала работать на полностью чистой ленте, в конце концов останавливается. Если машина за время вычислений записала n единиц на ленте, то говорят, что производительность машины равна n. Производительность любой машины, которая не останавливается, равна нулю. Производительность — это функция от описаний машины Тьюринга (натуральных чисел) к натуральным числам. Выражение p(T)=n будет означать, что производительность машины T равна n.
Среди машин Тьюринга, у которых есть конкретное число состояний, существует максимальная производительность, которой может обладать машина Тьюринга с данным количеством состояний. Она также представляет собой функцию от натуральных чисел (числа состояний) к натуральным числам (максимальной производительности машины с данным числом состояний). Мы запишем эту функцию в виде BB(k)=n, чтобы показать: максимальная производительность машины Тьюринга с k состояниями равна n. Может быть несколько различных машин с k состояниями и с максимальной производительностью, равной n. Каждую такую машину мы будем называть «усердным бобром» (Busy Beaver) для k.
Не существует машины Тьюринга, которая рассчитает функцию BB(k), то есть машины, которая, начав в стандартной конфигурации с k символами «1» на ленте, остановится в стандартной конфигурации, в которой на ленте будет BB(k) символов «1». Этот пример привел Тибор Радо (Radó 1962).
Доказательство несуществования такой функции начинается с допущения, что машина, которая начинает в стандартной конфигурации с k символами «1» на ленте и останавливается в стандартной конфигурации с BB(k) символами «1» на ленте, существует. Мы назовем такую машину B и примем, что она имеет k состояний.
Существует машина с n состояниями, записывающая n символов «1» на изначально чистой ленте (это задание для читателя). Мы можем построить новую машину, которая соединяет состояние остановки этой машины с начальным состоянием B, а затем соединяющую состояние остановки B с начальным состоянием другой копии B. Таким образом, первая машина пишет n символов «1», затем первая копия B вычисляет BB(n), но затем в дело вступает следующая копия B и считает BB(BB(n)). Общее число состояний одной машины равно n+2k. Наша машина является усердным бобром для n+2k, но она не более производительна, чем любая такая же машина. Итак (если усердный бобер существует):
BB(n+2k) ≥ BB(BB(n)) для любого значения n.
Несложно показать, что производительность машины Тьюринга возрастает при добавлении новых состояний, то есть
если i < j, то BB(i) < BB(j)
(еще одно задание). Следовательно (если усердный бобер существует):
n+2k ≥ BB(n) для любого значения n
Поскольку это верно для любого n, это верно для n+11, в результате чего получаем:
n+11+2k ≥ BB(n+11) для любого значения n
Но несложно показать, что BB(n+11) ≥ 2n (еще одно упражнение: покажите, что существует машина, располагающая одиннадцатью состояниями и предназначенная для удвоения количества символов «1» на ленте, и скомбинируйте такую машину с машиной, имеющей n состояний для записи n символов «1»). Сочетая этот факт с предыдущим неравенством, получаем:
n+11+2k ≥ BB(n+11) ≥ 2n для любого значения n
Вычитая n из обеих частей выражения, получаем 11+2k ≥ n для любого n, если усердный бобер существует, что является противоречием.
Хотя функция производительности невычислима, к поиску усердных бобров (наиболее производительных машин Тьюринга с заданным числом состояний) проявляется значительный интерес. Некоторые подходящие претенденты могут быть найдены по ссылкам в разделе «Интернет-ресурсы» настоящей статьи.
Проблема остановки
Полезно изучить описание машины Тьюринга и определить, не останавливается ли она при вводе определенных данных. Подобная трудность называется проблемой остановки и, к сожалению, является невычислимой. То есть не существует машины Тьюринга, способной вычислить функцию h(t,n), которая определяется как TRUE, если машина t останавливается при вводе n, а в противном случае — как FALSE.
Чтобы увидеть невычислимость функции остановки, представим, что такая машина H существует, и рассмотрим новую машину, совместив копирующую машину (см. рис. 4) с H, соединив состояние остановки копирующей машины с начальным состоянием машины H. Такая машина, начав на ленте с n символами «1», определяет, должна ли машина с кодом n останавливаться, когда в нее вводят n, то есть она вычисляет M(n) = h(n,n).
Теперь добавим еще одну небольшую машину к конечному состоянию H. Машина проходит бесконечную последовательность переходов, если лента содержит значение TRUE при начале работы машины, и останавливается, если лента содержит значение FALSE (упражнение для читателя — построить такую машину при условии, что TRUE записывается символами «11», а FALSE — символом «1»).
Эта полученная машина, назовем ее M, останавливается, если машина с кодом ввода n не останавливается на исходной ленте, содержащей n (ведь если машина n не останавливается на n, то останавливающаяся машина оставит на ленте значение TRUE и M будет выполнять бесконечную последовательность действий), и наоборот.
Чтобы увидеть невозможность этого, рассмотрим код самой машины M. Что происходит, когда M начинает работать с лентой, содержащей код машины M? Предположим, что M останавливается на M. Тогда по определению машины M она не останавливается. Но при этом, даже если она не останавливается на M, само определение M требует, чтобы машина остановилась.
Мы пришли к противоречию, а следовательно, останавливающаяся машина не существует. Невычислимость проблемы остановки по Тьюрингу была впервые доказана Тьюрингом в статье Turing 1937b. Данный результат применим и к реально существующим программам. Не существует компьютерной программы, которая могла бы проверить код программы и определить, остановится ли программа.
Альтернативные формулировки вычислимости
Рекурсивные функции
Теория рекурсивных функций изучает функции, которые могут быть определены с использованием рекурсивных методов (см. статью о рекурсивных функциях). Если кратко, то примитивные рекурсивные могут быть преобразованы из базовых функций:
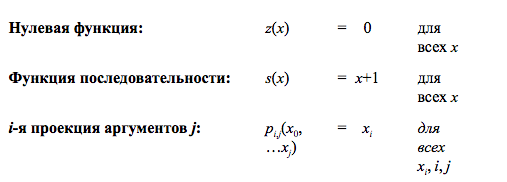
путем использования операции композиции и примитивной рекурсии:
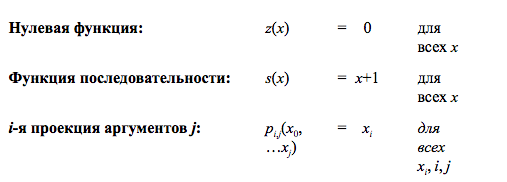
Рекурсивные функции образуются путем добавления оператора минимизации, который берет функцию f и выдает h указанным далее образом.
Минимизация:

Известно, что функции, вычислимые по Тьюрингу, представляют собой в точности эти рекурсивные функции.
Машины абак
Машины абак абстрактно связаны с более знакомой нам архитектурой современного цифрового компьютера (архитектурой фон Ноймана). В своей простейшей форме компьютер с такой архитектурой имеет некоторое количество адресуемых регистров (каждый из них может содержать одно значение) и процессор, который может считывать с них и записывать в них информацию.
Машина может выполнять две основные операции, а именно прибавлять единицу к содержанию определенного регистра (эту операцию мы обозначим n+, где n — имя регистра) и вычитать единицу (или пытаться это сделать) из указанного регистра с двумя возможными результатами: успех, если регистр изначально был ненулевым, и неуспех, если регистр был изначально нулевым (эту операцию мы обозначим n-).
Такие машины Ламбек (Lambek 1961) назвал компьютерами абак. Известно, что они эквивалентны машинам Тьюринга.
Современный цифровой компьютер ограничен конечностью своих элементов, от которой мы теоретически абстрагировались в определении машин абак, как и в случае машин Тьюринга. Физические компьютеры обладают ограничением по количеству ячеек памяти и их емкости, в то время как машины абак не подвергаются подобным ограничениям. Таким образом, некоторые функции, вычисляемые с помощью абака, невычислимы любой физической машиной. (Мы не будем рассматривать вопрос о том, остаются ли машины Тьюринга и современные цифровые компьютеры эквивалентными при внешнем вводе данных, поскольку такая постановка проблемы может потребовать изменить определение машины Тьюринга.)
Ограниченные машины Тьюринга
Определение машин Тьюринга можно изменить, исключив возможность записывать символы на ленту. Такие машины называют конечными автоматами. Вероятно, они менее мощны по сравнению с машинами Тьюринга, поскольку они не могут использовать ленту для запоминания состояния вычисления. Например, конечные автоматы не могут определить, состоит ли подаваемая на вход строка из символов «А», за которыми следует некоторое число символов «B». Причина в том, что машина не может запомнить, сколько символов «А» она увидела, кроме тех случаев, когда она находится в состоянии, представляющем этот факт. Для определения количества введенных символов «А» и «B» машина должна иметь бесконечное количество состояний (одно для запоминания, что она нашла одно «А», другое — для запоминания, что она нашла два символа и т.д.)
Библиография
Barwise, J. and Etchemendy, J., 1993, Turing's World, Stanford: CSLI Publications.
Boolos, G.S. and Jeffrey, R.C., 1974, Computability and Logic, Cambridge: Cambridge University Press.
Davis, M., 1958, Computability and Unsolvability, New York: McGraw-Hill; reprinted Dover, 1982.
Herken, R., (ed.), 1988, The Universal Turing Machine: A Half-Century Survey, New York: Oxford University Press.
Hodges, A., 1983, Alan Turing, The Enigma, New York: Simon and Schuster.
Kleene, S.C., 1936, “General Recursive Functions of Natural Numbers,” Mathematische Annalen, 112: 727–742.
Lambek, J., 1961, “How to Program an Infinite Abacus,” Canadian Mathematical Bulletin, 4: 279–293.
Lewis, H.R. and Papadimitriou, C.H., 1981, Elements of the Theory of Computation, Englewood Cliffs, NJ: Prentice-Hall.
Lin, S. and Radó, T., 1965, “Computer Studies of Turing Machine Problems,” Journal of the Association for Computing Machinery, 12: 196–212.
Petzold, G., 2008, “The Annotated Turing: A Guided Tour Through Alan Turing's Historic Paper on Computability and Turing Machines,”, Indianapolis, Indiana: Wiley.
Post, E., 1947, “Recursive Unsolvability of a Problem of Thue,” The Journal of Symbolic Logic, 12: 1–11.
Radó, T., 1962, “On Non-computable functions,” Bell System Technical Journal, 41 (May): 877–884.
Turing, A.M., 1937a, “On Computable Numbers, With an Application to the Entscheidungsproblem,” Proceedings of the London Mathematical Society, s2-42 (1): 230–265; correction ibid., (1938) s2-43 (1): 544–546. [Note: This paper was received May 28, 1936 and read to the Society on November 12, 1936, but wasn't actually published until 1937.]
Turing, A.M., 1937b, “Computability and λ-Definability,” The Journal of Symbolic Logic, 2: 153–163.
Интернет-ресурсы
“Turing Machines”, Stanford Encyclopedia of Philosophy (Summer 2003 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/sum2003/entries/turing-machine/>. [Исходная версия настоящей статьи, написанная редакторами Стэнфордской энциклопедии философии.]
Веб-сайт Алана Тьюринга
Блетчли-парк, Великобритания, особняк, в котором Алан Тьюринг в ходе мировой войны работал в шифровальном подразделении Station X.

.jpg)




.jpg)
.jpg)







